Аэродинамическое сопротивление Калькулятор | Вычислить Аэродинамическое сопротивление
✖Плотность воздуха взята при стандартных условиях.ⓘ Плотность воздуха [ρ] | сантиграмм / литрдециграмм/ литрдекаграмм / литрПлотность Землифемтограмм/ литрЗерно на кубический футЗерно на галлон (Великобритания)Зерно на галлон (США)Грамм на кубический сантиметрГрамм на кубический метрГрамм на кубический миллиметрГрамм на литрГрамм на миллилитргектограмм / литрКилограмм на кубический сантиметрКилограмм на кубический дециметрКилограмм на кубический метрКилограмм на литрмегаграмм / литрмикрограмм / литрМиллиграмм на кубический сантиметрМиллиграмм на кубический метрМиллиграмм на кубический миллиметрМиллиграмм на литрнанограмм / литрУнция на кубический футУнция на кубический дюймУнция на галлон (Великобритания)Унция на галлон (США)пикограмм / литрПланковская плотностьФунт на кубический футФунт на кубический дюймФунт на кубический ярдФунт на галлон (Великобритания)Фунт на галлон (США)Слаг на кубический футСлаг на кубический дюймСлаг на кубический ярдТонна (длинная) на кубический ярдТонна (короткая) на кубический ярд | +10% -10% | |
✖Фронтальная площадь транспортного средства определяется как площадь на плоскости проекции транспортного средства, если смотреть спереди. | акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad | +10% -10% | |
✖Крейсерская скорость транспортного средства – это постоянная скорость, которую транспортное средство поддерживает во время движения.ⓘ Крейсерская скорость автомобиля [Vc] | Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость прежде всегоКосмическая скорость СекундаКосмическая скорость третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометры / часКилометр в минутуКилометры / секМорской узелУзел (Великобритания)МахаМаха (стандарт СИ)Метр в часМетр в минутуметр в секундумили / часмили / минутумили / секМиллиметр в деньМиллиметр / часМиллиметр в минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% | |
✖Коэффициент сопротивления потока — это безразмерная величина, которая используется для количественной оценки сопротивления или сопротивления объекта в жидкой среде, такой как воздух или вода. | +10% -10% |
|
✖Аэродинамическое сопротивление транспортного средства определяется как сила сопротивления, создаваемая частицами воздуха при движении транспортного средства на более высоких скоростях.ⓘ Аэродинамическое сопротивление [Fa] |
Атомная единица силыАттоньютонСантиньютонДеканьютонДециньютондинаэксаньютонFemtonewtonГиганьютонГрамм-силаГраве-силагектоньютонДжоуль / СантиметрДжоуль на метрКилограмм-силаКилоньютонКилопруд Килофунт-силаКип-силаМеганьютонМикроньютонMilligrave — силаМиллиньютонНаноньютонНьютонУнция-силаPetanewtonPiconewtonпрудФунт-фут в квадратную секундуПаундалФунт-силастенТераньютонТон-сила (Long)Тон-сила (метрическая система)Тон-сила (короткий)Йоттаньютон |
⎘ копия |
👎
Формула
сбросить
👍
Аэродинамическое сопротивление Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Плотность воздуха: 1.293 Килограмм на кубический метр —> 1.293 Килограмм на кубический метр Конверсия не требуется
Передняя часть автомобиля: 1.5 Квадратный метр —> 1.5 Квадратный метр Конверсия не требуется
Крейсерская скорость автомобиля: 22 метр в секунду —> 22 метр в секунду Конверсия не требуется
Коэффициент сопротивления потока: 0.47 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
220.59873 Ньютон —> Конверсия не требуется
< 14 Трансмиссия Калькуляторы
Угловое ускорение ведомого вала
Идти Угловое ускорение ведомого вала = -(Угловая скорость ведомого вала^2)*cos(Угол между ведущим и ведомым валами)*(sin(Угол между ведущим и ведомым валами)^2)*sin(2*Угол поворота ведомого вала)/(1-(cos(Угол поворота ведомого вала)^2)*(sin(Угол между ведущим и ведомым валами)^2))
Процент преодолеваемого подъема автомобиля
Идти Преодолеваемый подъем автомобиля = ((10200*Крутящий момент двигателя в ньютонах*Общая редукторная передача)/(Радиус качения нагруженной ведущей шины*Полная масса транспортного средства))-Сопротивление качению в процентах
Коэффициент скорости сустава Гука
Идти Коэффициент скорости = cos(Угол между ведущим и ведомым валами)/(1-((cos(Угол поворота приводным валом))^2)*(sin(Угол между ведущим и ведомым валами))^2)
Осевая сила многодискового сцепления с использованием теории равномерного износа
Идти
Общая осевая нагрузка = (pi*Давление интенсивности*Внутренний диаметр фрикционного диска*(Внешний диаметр фрикционного диска-Внутренний диаметр фрикционного диска))*0. 2*Коэффициент сопротивления потока)
2*Коэффициент сопротивления потока)
Тяга дышла
Идти Тяга дышла = ((Крутящий момент двигателя в ньютонах*Общая редукторная передача*1000)/Радиус качения нагруженной ведущей шины)-Сопротивление качению на колесе
Мощность, необходимая для движения автомобиля
Идти Мощность, необходимая для движения автомобиля = (Общее сопротивление на транспортном средстве*Скорость автомобиля в метрах в секунду)/КПД трансмиссии автомобиля
Общее сопротивление на транспортном средстве
Идти Общее сопротивление на транспортном средстве = Аэродинамическое сопротивление автомобиля+Сопротивление качению на колесе+Градиентное сопротивление
Вес на переднюю ось
Идти Вес на переднюю ось = (Общий распределяемый вес автомобиля*Расстояние CG от задней оси)/Колесная база автомобиля
Вес на задней оси
Идти Вес на задней оси = (Общий распределяемый вес автомобиля*Расстояние CG от передней оси)/Колесная база автомобиля
Эффективное передаточное число
Идти Эффективное передаточное число = (Диаметр старой шины/Новый диаметр шины)*Передаточное отношение трансмиссии
Крутящий момент двигателя
Идти
Крутящий момент двигателя = (9. 55*Мощность, необходимая для движения автомобиля)/Скорость двигателя в об/мин
55*Мощность, необходимая для движения автомобиля)/Скорость двигателя в об/мин
Передаточное число конечной передачи
Идти Передаточное число конечной передачи = Передаточное число задней передачи*Коэффициент овердрайва
Шаг шестерни
Идти Шаг шестерни = Предыдущий номер нижнего передаточного числа/Передаточное число
Аэродинамическое сопротивление формула
Аэродинамическое сопротивление автомобиля = (0. 2*CD)
2*CD)
Share
Copied!Что такое сила сопротивления воздуха?
Мы настолько привыкли к тому, что окружены воздухом, что зачастую не обращаем на это внимания. Речь здесь идет, прежде всего, о прикладных технических задачах, при решении которых на первых порах забывается, что существует сила сопротивления воздуха.
Мы настолько привыкли к тому, что окружены воздухом, что зачастую не обращаем на это внимания. Речь здесь идет, прежде всего, о прикладных технических задачах, при решении которых на первых порах забывается, что существует сила сопротивления воздуха.
Она напоминает о себе практически при любом действии. Хоть мы поедем на автомобиле, хоть полетим на самолете, даже если будем просто кидать камень. Вот и попробуем понять, что собой представляет сила сопротивления воздуха на примере простых случаев.
Вы не задумывались, почему автомобили имеют такую обтекаемую форму и ровную поверхность? А ведь все на самом деле очень понятно.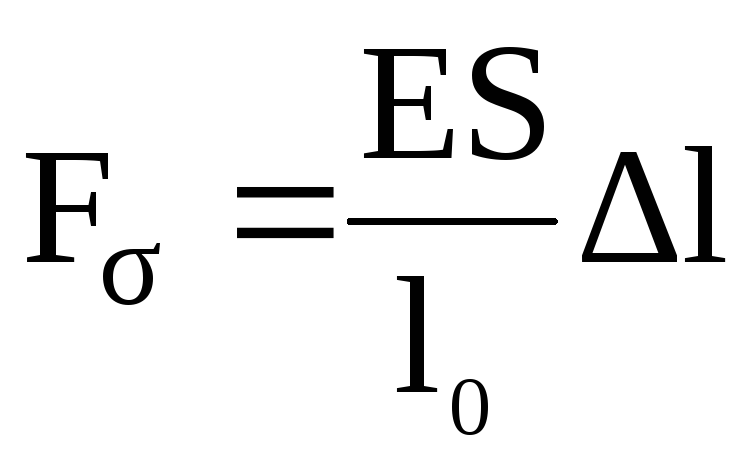 Сила сопротивления воздуха складывается из двух величин – из сопротивления трения поверхности тела и сопротивления формы тела. С целью уменьшения силы трения и добиваются уменьшения неровностей и шероховатостей на внешних деталях при изготовлении автомобилей и любых иных транспортных средств.
Сила сопротивления воздуха складывается из двух величин – из сопротивления трения поверхности тела и сопротивления формы тела. С целью уменьшения силы трения и добиваются уменьшения неровностей и шероховатостей на внешних деталях при изготовлении автомобилей и любых иных транспортных средств.
Для этого их грунтуют, окрашивают, полируют и лакируют. Подобная обработка деталей приводит к тому, что сопротивление воздуха, воздействующее на автомобиль, уменьшается, повышается скорость автомобиля и уменьшается расход топлива при движении. Наличие силы сопротивления объясняется тем, что при движении автомобиля воздух сжимается и перед ним создается область местного повышенного давления, а за ним, соответственно, область разрежения.
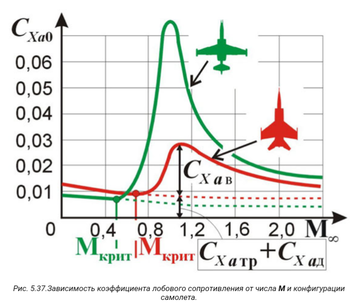
Надо отметить, что при повышенных скоростях движения машины основной вклад в сопротивление вносит форма авто. Сила сопротивления, формула расчета которой приведена ниже, определяет факторы, от которых она зависит.
Сила сопротивления = Сх*S*V2*r/2
где S – площадь передней проекции машины;
Cx – коэффициент, учитывающий аэродинамическое сопротивление;
V – скорость движения;
r — плотность воздуха.
Как нетрудно заметить из приведенной формулы, сила сопротивления не зависит от массы автомобиля. Основной вклад вносят два компонента – квадрат скорости и форма автомобиля. Т.е. при повышении скорости движения в два раза в четыре раза увеличится сопротивление. Ну и поперечное сечение автомобиля оказывает значительное влияние. Чем более обтекаемым будет автомобиль, тем меньше сопротивление воздуха.
И в формуле есть еще параметр, который просто требует обратить на него пристальное внимание – плотность воздуха. Но его влияние уже более заметно при полетах самолетов. Как известно, с повышением высоты уменьшается плотность воздуха. Значит, соответственно будет уменьшаться сила его сопротивления. Однако и для самолета на величину оказываемого сопротивления будут по-прежнему влиять те же факторы – скорость движения и форма.
Не менее любопытной является история изучения влияния воздуха на точность стрельбы. Работы подобного характера велись давно, первые их описания относятся к 1742 году. Эксперименты проводились в разных странах, с различной формой пуль и снарядов. В итоге проведения исследований была определена оптимальная форма пули и соотношение ее головной и хвостовой части, разработаны баллистические таблицы поведения пули в полете.
Эксперименты проводились в разных странах, с различной формой пуль и снарядов. В итоге проведения исследований была определена оптимальная форма пули и соотношение ее головной и хвостовой части, разработаны баллистические таблицы поведения пули в полете.
В дальнейшем проводились исследования зависимости полета пули от ее скорости, продолжала отрабатываться форма пули, а также совершенствовалась методика исследования. Были разработаны математические модели и создан специальный математический инструмент – баллистический коэффициент. Он показывает соотношение сил аэродинамического сопротивления и сил инерции, действующих на пулю.
В статье рассмотрено, что собой представляет сила сопротивления воздуха, дана формула, позволяющая определить величину и степень влияния различных факторов на величину сопротивления, рассмотрено его воздействие в разных областях техники.
Перетаскивание зависит от
плотность
воздуха, квадрат скорости,
вязкость и сжимаемость воздуха,
размер и форма
тело и склонность тела к
поток. Один из способов справиться со сложными зависимостями — охарактеризовать зависимость от одной переменной. Для перетаскивания эта переменная называется коэффициент аэродинамического сопротивления, обозначенный 92 Для данного воздуха условиях, форме и наклоне объекта, мы должны определить значение для Cd для определения сопротивления. Определение стоимости коэффициент лобового сопротивления сложнее, чем определение коэффициент подъемной силы из-за многократного источники сопротивления. Приведенный выше коэффициент лобового сопротивления включает форму компоненты сопротивления, сопротивления поверхностного трения и волнового сопротивления. Коэффициенты аэродинамического сопротивления почти всегда определяется опытным путем с помощью аэродинамическая труба. Обратите внимание, что площадь (A), заданная в уравнении сопротивления, представлена как опорная область .  Но
сопротивление одинаково, а коэффициенты связаны отношением
области. На практике коэффициенты аэродинамического сопротивления сообщаются на основе
широкий выбор площадей объектов. В отчете инженер-испытатель должен
укажите используемую площадь; при использовании данных читателю, возможно, придется
преобразовать коэффициент лобового сопротивления, используя соотношение площадей. Но
сопротивление одинаково, а коэффициенты связаны отношением
области. На практике коэффициенты аэродинамического сопротивления сообщаются на основе
широкий выбор площадей объектов. В отчете инженер-испытатель должен
укажите используемую площадь; при использовании данных читателю, возможно, придется
преобразовать коэффициент лобового сопротивления, используя соотношение площадей. В приведенном выше уравнении плотность обозначается как греческая буква «ро». Мы не используем «d» для плотности так как «d» часто используется указать расстояние. Сочетание термины «плотность, умноженная на квадрат скорости, деленный на два» называется динамическое давление и появляется у Бернулли уравнение давления. Экскурсии с гидом
Деятельность: Связанные сайты: |
6.
 4 Сила лобового сопротивления и предельная скорость — Университетская физика, том 1
4 Сила лобового сопротивления и предельная скорость — Университетская физика, том 1Цели обучения
К концу этого раздела вы сможете:
- Выразите силу сопротивления математически
- Описать применение силы сопротивления
- Определить конечную скорость
- Определить конечную скорость объекта по его массе
Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. Чем быстрее вы двигаете рукой, тем труднее двигаться. Вы чувствуете меньшую силу сопротивления, когда наклоняете руку так, чтобы только сторона проходила через воздух — вы уменьшили площадь своей руки, обращенную в направлении движения.
Силы сопротивления
Как и трение, сила сопротивления всегда противодействует движению объекта. В отличие от простого трения, сила сопротивления пропорциональна некоторой функции скорости объекта в этой жидкости. Эта функциональность сложна и зависит от формы объекта, его размера, его скорости и жидкости, в которой он находится. Для большинства крупных объектов, таких как велосипедисты, автомобили и бейсбольные мячи, движущихся не слишком медленно, величина силы сопротивления FDFD пропорциональна квадрату скорости тела. Мы можем записать это соотношение математически как FD∝v2.FD∝v2. При учете других факторов эта связь становится
В отличие от простого трения, сила сопротивления пропорциональна некоторой функции скорости объекта в этой жидкости. Эта функциональность сложна и зависит от формы объекта, его размера, его скорости и жидкости, в которой он находится. Для большинства крупных объектов, таких как велосипедисты, автомобили и бейсбольные мячи, движущихся не слишком медленно, величина силы сопротивления FDFD пропорциональна квадрату скорости тела. Мы можем записать это соотношение математически как FD∝v2.FD∝v2. При учете других факторов эта связь становится
6,5
, где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρρ — плотность жидкости. (Напомним, что плотность — это масса на единицу объема.) Это уравнение также можно записать в более обобщенном виде: FD=bvn, FD=bvn, где b — константа, эквивалентная 0,5CρA.0,5CρA. Мы установили показатель степени n для этих уравнений равным 2, потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости.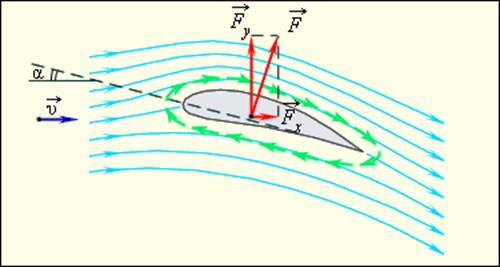
Сила сопротивления
Сила сопротивления FDFD пропорциональна квадрату скорости объекта. Математически
FD=12CρAv2,FD=12CρAv2,
, где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρρ — плотность жидкости.
Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время гонки (рис. 6.29). Аэродинамическая форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.
Рисунок
6,29
От гоночных автомобилей до гонщиков бобслея аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости и имеет форму пули с коническими плавниками. (кредит: «Армия США»/Wikimedia Commons)
(кредит: «Армия США»/Wikimedia Commons)
Значение коэффициента сопротивления C определяют опытным путем, обычно с применением аэродинамической трубы (рис. 6.30).
Рисунок 6.30 Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)
Коэффициент лобового сопротивления может зависеть от скорости, но мы предполагаем, что здесь он является константой. В таблице 6.2 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На шоссейных скоростях более 50% 50% мощности автомобиля расходуется на преодоление сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). По этой причине во время нефтяного кризиса 1970-х годов в США максимальная скорость на шоссе была установлена на уровне около 9 км/ч.0 км/ч (55 миль/ч).
| Объект | С |
|---|---|
| Аэродинамический профиль | 0,05 |
| Тойота Камри | 0,28 |
| Форд Фокус | 0,32 |
| Хонда Сивик | 0,36 |
| Феррари Тестаросса | 0,37 |
| пикап Dodge Ram | 0,43 |
| Сфера | 0,45 |
| Внедорожник Hummer h3 | 0,64 |
| Парашютист (ноги вперед) | 0,70 |
| Велосипед | 0,90 |
| Парашютист (горизонтальный) | 1,0 |
| Круглая плоская пластина | 1,12 |
Стол
6. 2
Типичные значения коэффициента лобового сопротивления C
2
Типичные значения коэффициента лобового сопротивления C
В мире спорта ведутся масштабные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (рис. 6.31). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила.
Рисунок
6.31
Боди-костюмы, такие как этот LZR Racer Suit, помогли установить множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % 10 % меньше сопротивления. (кредит: НАСА/Кэти Барнсторфф)
Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % 10 % меньше сопротивления. (кредит: НАСА/Кэти Барнсторфф)
Предельная скорость
Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении действия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета малой выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорения нет, как показывает второй закон Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своей конечной скорости (vT). (vT). Поскольку FDFD пропорционален квадрату скорости, более тяжелый парашютист должен двигаться быстрее, чтобы FDFD сравнялся с его весом. Давайте посмотрим, как это работает более количественно.
(vT). Поскольку FDFD пропорционален квадрату скорости, более тяжелый парашютист должен двигаться быстрее, чтобы FDFD сравнялся с его весом. Давайте посмотрим, как это работает более количественно.
На предельной скорости,
Fnet=mg-FD=ma=0.Fnet=mg-FD=ma=0.
Таким образом,
мг=ФД.мг=ФД.
Используя уравнение для силы сопротивления, мы имеем
мг=12CρAvT2.мг=12CρAvT2.
Решая скорость, получаем
vT=2мгρCA.vT=2мгρCA.
Предположим, что плотность воздуха равна ρ=1,21 кг/м3. ρ=1,21 кг/м3. Парашютист весом 75 кг, спускающийся вниз головой вперед, имеет площадь поперечного сечения приблизительно A=0,18 м2, A=0,18 м2 и коэффициент сопротивления приблизительно C=0,70C=0,70. Мы находим, что
vT=2(75кг)(9,80м/с2)(1,21кг/м3)(0,70)(0,18м2)=98м/с=350км/ч.vT=2(75кг)(9,80м/с2)(1,21кг /м3)(0,70)(0,18м2)=98м/с=350км/ч.
Это означает, что парашютист массой 75 кг достигает конечной скорости около 350 км/ч, путешествуя головой вперед, сводя к минимуму площадь и сопротивление.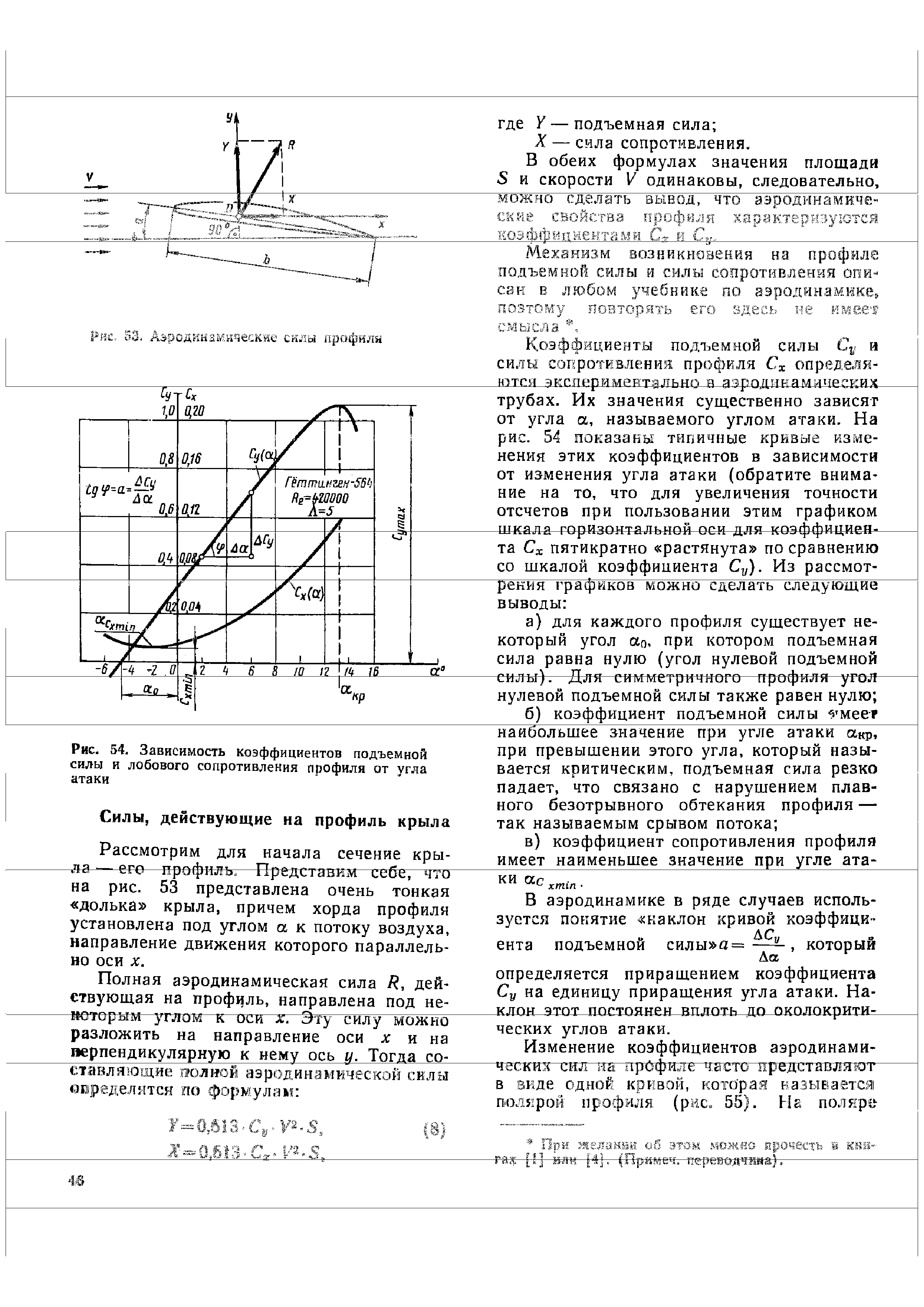 В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.
В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.
Пример 6.17
Предельная скорость парашютиста
Найдите конечную скорость парашютиста массой 85 кг, падающего с распростертым орлом. Предположим, что в положении орла ныряльщик имеет площадь поперечного сечения 0,70 м20,70 м2.Стратегия
При конечной скорости Fnet=0.Fnet=0. Таким образом, сила сопротивления парашютиста должна равняться силе тяжести (весу человека). Используя уравнение силы сопротивления, находим mg=12ρCAv2.mg=12ρCAv2.Раствор
Конечная скорость vTvT может быть записана какvT=2мгρCA=2(85кг)(9,80м/с2)(1,21кг/м3)(1,0)(0,70м2)=44м/с.vT=2мгρCA=2(85кг)(9,80м/с2)(1,21 кг/м3)(1,0)(0,70м2)=44м/с.
Значение
Этот результат согласуется со значением для vTvT, упомянутым ранее. Парашютист весом 75 кг, идущий вперед ногами, имел конечную скорость vT=98 м/с. vT=98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха.
Парашютист весом 75 кг, идущий вперед ногами, имел конечную скорость vT=98 м/с. vT=98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха.Проверьте свое понимание 6.10
Найдите предельную скорость 50-килограммового парашютиста, падающего распростертым орлом.
Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, а белка достигает.
Следующая интересная цитата о размере животного и конечной скорости взята из 1928 эссе британского биолога Дж. Б. С. Холдейна под названием «О правильном размере».
«Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крысу убили, человека сломали, а лошадь забрызгала. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз больше, чем движущая сила».
Крысу убили, человека сломали, а лошадь забрызгала. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз больше, чем движущая сила».
Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Эта зависимость определяется законом Стокса.
Закон Стокса
Для сферического объекта, падающего в среду, сила сопротивления равна
Fs=6πrηv,Fs=6πrηv,6,6
, где r — радиус объекта, ηη — вязкость жидкости, а v — скорость объекта.
Хорошими примерами закона Стокса являются микроорганизмы, пыльца и частицы пыли. Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) (1 мкм) может составлять около 2 мкм/с. 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку.
Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) (1 мкм) может составлять около 2 мкм/с. 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку.
Осадок в озере может двигаться с большей конечной скоростью (около 5 мкм/с), 5 мкм/с, поэтому может пройти несколько дней, прежде чем он достигнет дна озера после отложения на поверхности.
Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, образуя обтекаемую форму (рис. 6.32). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию.
Стаи птиц летят в форме наконечника копья, образуя обтекаемую форму (рис. 6.32). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию.
Рисунок 6.32 Гуси летят V-образным строем во время своих длительных миграционных путешествий. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (кредит: модификация работы «Julo»/Wikimedia Commons)
Интерактивный
В демонстрационных лекциях мы проводим измерения силы сопротивления различных объектов. Объекты помещаются в однородный воздушный поток, создаваемый вентилятором. Вычислите коэффициент сопротивления.
Расчет сил трения, зависящих от скорости
Когда тело скользит по поверхности, сила трения на нем приблизительно постоянна и определяется выражением µkN.µkN. К сожалению, сила трения на тело, движущееся через жидкость или газ, не ведет себя так просто.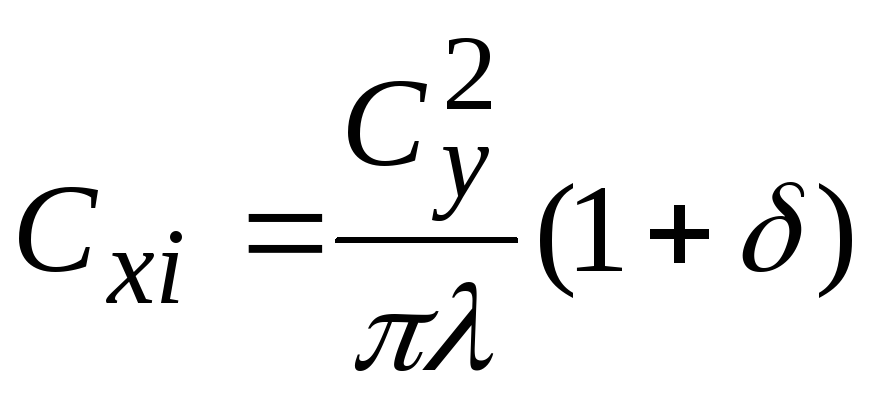 Эта сила сопротивления обычно является сложной функцией скорости тела. Однако для тела, движущегося по прямой с умеренной скоростью через жидкость, например воду, сила трения часто может быть приблизительно равна
Эта сила сопротивления обычно является сложной функцией скорости тела. Однако для тела, движущегося по прямой с умеренной скоростью через жидкость, например воду, сила трения часто может быть приблизительно равна
fR=-bv, fR=-bv,
, где b — постоянная, значение которой зависит от размеров и формы тела и свойств жидкости, а v — скорость тела. Две ситуации, для которых сила трения может быть представлена этим уравнением, — это моторная лодка, движущаяся по воде, и небольшой объект, медленно падающий через жидкость.
Рассмотрим объект, падающий в жидкость. Диаграмма свободного тела этого объекта с положительным направлением вниз показана на рис. 6.33. Второй закон Ньютона в вертикальном направлении дает дифференциальное уравнение
мг-бв=мдвдт, мг-бв=мдвдт,
, где мы записали ускорение как dv/dt.dv/dt. По мере увеличения против сила трения – bv увеличивается до тех пор, пока не совпадет с мг .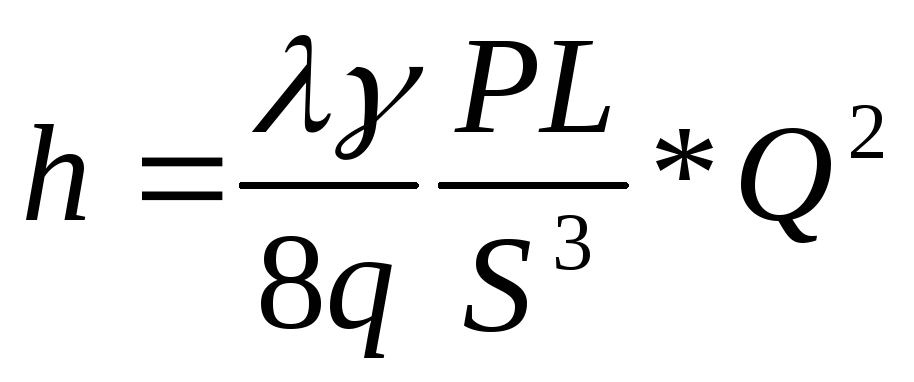 В этот момент ускорение отсутствует, и скорость остается постоянной на уровне конечной скорости vT.vT. Из предыдущего уравнения
В этот момент ускорение отсутствует, и скорость остается постоянной на уровне конечной скорости vT.vT. Из предыдущего уравнения
мг-бвТ=0, мг-бвТ=0,
так
vT=mgb.vT=mgb.
Рисунок 6.33 Схема свободного тела объекта, падающего через резистивную среду.
Мы можем найти скорость объекта, интегрируя дифференциальное уравнение для v . Во-первых, мы переставляем члены в этом уравнении, чтобы получить
dvg-(b/m)v=dt.dvg-(b/m)v=dt.
Предполагая, что v=0att=0,v=0att=0, интегрирование этого уравнения дает
∫0vdv′g−(b/m)v′=∫0tdt′,∫0vdv′g−(b/m)v′=∫0tdt′,
или
−mbln(g−bmv′)|0v=t′|0t,−mbln(g−bmv′)|0v=t′|0t,
, где v’andt’v’andt’ — фиктивные переменные интегрирования. В заданных пределах находим
-mb[ln(g-bmv)-lng]=t.-mb[ln(g-bmv)-lng]=t.
Поскольку lnA−lnB=ln(A/B),lnA−lnB=ln(A/B) и ln(A/B)=ximpliesex=A/B, ln(A/B)=ximpliesex=A/B , получаем
g-(bv/m)g=e-bt/m,g-(bv/m)g=e-bt/m,
и
v=mgb(1-e-bt/м). v=mgb(1-e-bt/м).
v=mgb(1-e-bt/м).
Обратите внимание, что при t→∞,v→mg/b=vT,t→∞,v→mg/b=vT, что является конечной скоростью.
Позиция в любое время может быть найдена путем интегрирования уравнения для v . С v=dy/dt, v=dy/dt,
dy=mgb(1−e−bt/m)dt.dy=mgb(1−e−bt/m)dt.
Предполагая, что y=0, когда=0,y=0, когда=0,
∫0ydy’=mgb∫0t(1-e-bt’/m)dt’, ∫0ydy’=mgb∫0t(1-e-bt’/m)dt’,
, который интегрируется в
y=mgbt+m2gb2(e−bt/m−1).y=mgbt+m2gb2(e−bt/m−1).
Пример 6.18
Влияние силы сопротивления на моторную лодку
Моторная лодка движется по озеру со скоростью v0v0, когда ее мотор внезапно замерзает и останавливается. Затем лодка замедляется под действием силы трения fR=−bv.fR=−bv. а) Каковы скорость и положение лодки как функции времени? б) Если за 10 с скорость лодки уменьшается с 4,0 до 1,0 м/с, какой путь она пройдет до остановки?Решение
- При остановленном двигателе единственная горизонтальная сила, действующая на лодку, равна fR=−bv,fR=−bv, поэтому из второго закона Ньютона
мдвдт=-бв, мдвдт=-бв,
который мы можем записать какdvv=-bmdt.
Интегрируя это уравнение между нулевым моментом времени, когда скорость равна v0v0, и временем t , когда скорость равна vv, мы имеем dvv=-bmdt.
dvv=-bmdt.∫0vdv′v′=−bm∫0tdt′.∫0vdv′v′=−bm∫0tdt′.
Таким образом,lnvv0=-bmt,lnvv0=-bmt,
что, поскольку lnA=ximpliesex=A,lnA=ximpliesex=A, мы можем записать это какv=v0e-bt/m.v=v0e-bt/m.
Теперь из определения скоростиdxdt=v0e-bt/м, dxdt=v0e-bt/м,
так что у нас естьdx=v0e-bt/mdt.dx=v0e-bt/mdt.
С начальным положением ноль имеем∫0xdx’=v0∫0te-bt’/mdt’, ∫0xdx’=v0∫0te-bt’/mdt’,
иx=-mv0be-bt’/m|0t=mv0b(1-e-bt/m).x=-mv0be-bt’/m|0t=mv0b(1-e-bt/m).
С увеличением времени e−bt/m→0,e−bt/m→0, и положение лодки приближается к предельному значениюхмакс=mv0b.xмакс=mv0b.
Хотя это говорит нам о том, что лодке требуется бесконечное количество времени, чтобы достичь xmax,xmax, лодка эффективно останавливается через разумное время. Например, при t=10м/б,t=10м/б имеемv=v0e-10≃4,5×10-5v0,v=v0e-10≃4,5×10-5v0,
тогда как у нас также естьx=xmax(1−e−10)≃0,99995xmax.
Таким образом, скорость и положение лодки практически достигли своих конечных значений. x=xmax(1−e−10)≃0,99995xmax.
x=xmax(1−e−10)≃0,99995xmax. - При v0=4,0 м/sv0=4,0 м/с и v=1,0 м/с, v=1,0 м/с получаем 1,0 м/с=(4,0 м/с)e−(b/м)(10 с ), 1,0 м/с = (4,0 м/с) e−(b/m)(10 с), поэтому
ln0.25=-ln4.0=-bm(10s),ln0.25=-ln4.0=-bm(10s),
иbm=110ln4.0s-1=0.14s-1.bm=110ln4.0s-1=0.14s-1.
Теперь предельное положение лодкиxmax=mv0b=4,0 м/с0,14с-1=29м.xmax=mv0b=4,0м/с0,14с-1=29м.
Значение
В обоих предыдущих примерах мы нашли «предельные» значения. Конечная скорость такая же, как и предельная скорость, то есть скорость падающего объекта по прошествии (относительно) длительного времени. Точно так же предельное расстояние лодки — это расстояние, которое лодка пройдет по прошествии большого количества времени. Из-за свойств экспоненциального затухания время, необходимое для достижения любого из этих значений, на самом деле не слишком велико (конечно, не бесконечное количество времени!), но они быстро находятся, если довести предел до бесконечности.

 ⓘ Передняя часть автомобиля [A]
ⓘ Передняя часть автомобиля [A]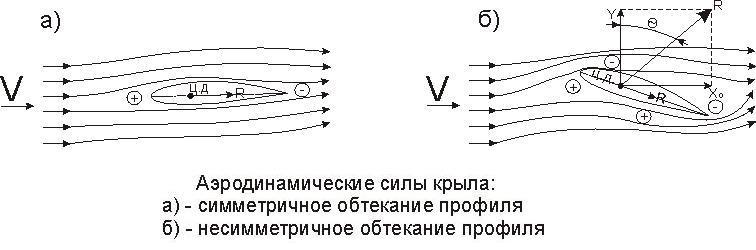
 В целом зависимость от формы тела, наклона, воздуха
вязкость и сжимаемость очень сложны.
В целом зависимость от формы тела, наклона, воздуха
вязкость и сжимаемость очень сложны. Перетаскивание напрямую зависит от размера
тела. Поскольку мы имеем дело с аэродинамическими
сил зависимость может быть охарактеризована некоторой площадью. Но
какой район выбираем? Если мы думаем, что сопротивление вызвано
трения между воздухом и телом, логичным выбором было бы
общая площадь поверхности тела. Если мы думаем о перетаскивании как о
сопротивление потоку, более логичным выбором будет лобовое
участок тела, перпендикулярный направлению потока. И
наконец, если мы хотим сравнить с коэффициентом подъемной силы, мы должны
используйте ту же площадь крыла, которая использовалась для получения коэффициента подъемной силы. Поскольку
Коэффициент лобового сопротивления обычно определяют экспериментально путем измерения
перетащите и область, а затем выполните деление, чтобы получить
коэффициент, мы можем использовать
Перетаскивание напрямую зависит от размера
тела. Поскольку мы имеем дело с аэродинамическими
сил зависимость может быть охарактеризована некоторой площадью. Но
какой район выбираем? Если мы думаем, что сопротивление вызвано
трения между воздухом и телом, логичным выбором было бы
общая площадь поверхности тела. Если мы думаем о перетаскивании как о
сопротивление потоку, более логичным выбором будет лобовое
участок тела, перпендикулярный направлению потока. И
наконец, если мы хотим сравнить с коэффициентом подъемной силы, мы должны
используйте ту же площадь крыла, которая использовалась для получения коэффициента подъемной силы. Поскольку
Коэффициент лобового сопротивления обычно определяют экспериментально путем измерения
перетащите и область, а затем выполните деление, чтобы получить
коэффициент, мы можем использовать 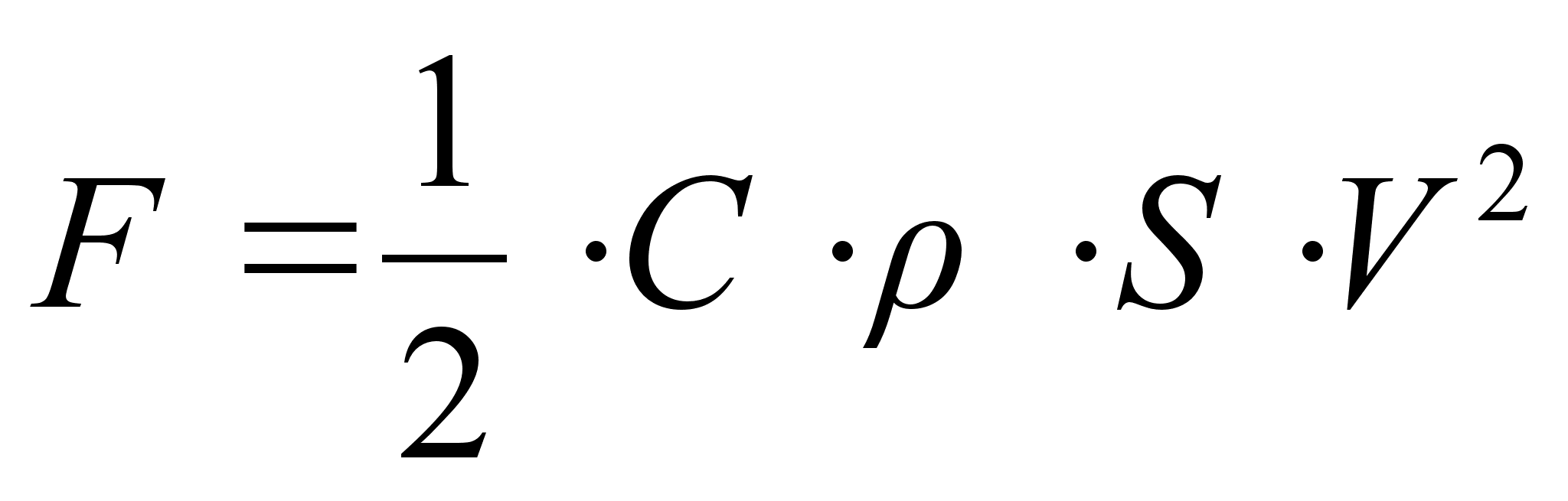 dvv=-bmdt.
dvv=-bmdt. x=xmax(1−e−10)≃0,99995xmax.
x=xmax(1−e−10)≃0,99995xmax.