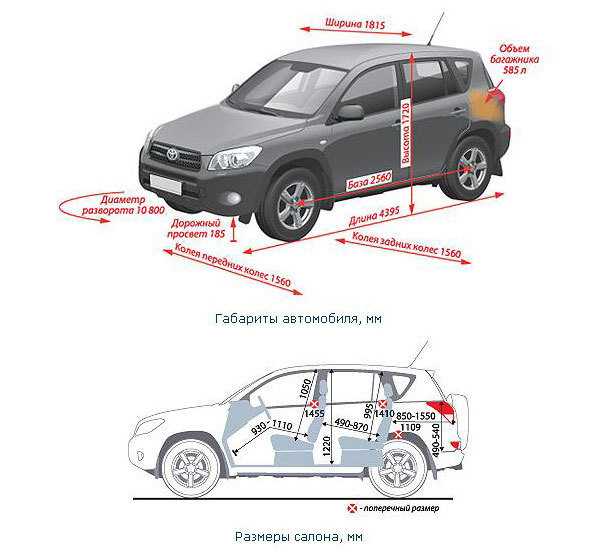
Тойота РАВ4 2009 габаритные размеры: клиренс, длина, высота

Габаритные размеры Тойота РАВ4 2009

Автолюбители частенько ищут данные про такие популярные автомобильные габариты как длина, ширина и высота авто, когда сомневаются, заедет ли их железный конь в гараж либо же не хотят иметь проблем с парковкой в городе. Вопрос габаритов авто также зачастую волнует начинающих водителей либо же людей, которые задумали сменить машину.

Стоит понимать, что помимо базовых габаритов есть еще и другие параметры, на которые стоит обратить внимание. Например, более короткая колесная база повышает маневренность, что немаловажно, если вам приходится много лавировать в городском потоке по узким улочкам, вписываться в крутые повороты и т.д. С другой стороны, удлиненная колесная база придает автомобилю устойчивости, правда, она же заставляет быть предельно осторожным при переезде высоких преград, бугров и кочек.

Внешние размеры Тойота РАВ4 2009

Длина машины	459. 994 см
Ширина	181.61 — 185.42 см
Высота	168.402 — 174.498 см
Колесная база	265.938 см
Радиус разворота	44.196 — 46.736 см
Клиренс
Коэффициент аэродинамического сопротивления	0.33
Передняя колея	155.956 см
Задняя	155. 956 см

Передняя и задняя ширина колеи автомобиля Тойота РАВ4 2009 года
Ширина колеи может оказывать существенное влияние на ощущения от вождения авто, поэтому: чем больше расстояние между колесами на одной и той же оси – тем лучше автомобиль входит в крутые повороты на трассе.

Радиус разворота автомобиля Тойота РАВ4 2009 года
Радиус разворота дает представление о наименьшем радиусе воображаемого круга, по которому автомобиль может выполнить разворот на дороге. Данная габаритная величина – хороший индикатор, который говорит о маневренности авто.

Клиренс автомобиля Тойота РАВ4 2009 года
Дорожный просвет или же по ненашенскому – клиренс – измеряет расстояние между плоской поверхностью и самой нижней точкой днища. Клиренс должен замеряться на стандартных размерах шин.

Коэффициент аэродинамического сопротивления автомобиля Тойота РАВ4 2009 года
Коэффициент сопротивления описывает аэродинамические характеристики автомобиля, указывая на уровень сопротивления воздуха при движении. Дизайн автомобиля очень сильно влияет на этот показатель, поэтому для седанов коэффициент сопротивления будет меньшим, нежели у кроссоверов и джипов из-за их угловатых очертаний.

2009 Тойота РАВ4 размеры интерьера

Head Room — Front	103.632 см
Head Room — Rear	100.838 см
Head Room — Third Row	94.488 см
Hip Room — Front	136.652 см
Hip Room — Rear	133.096 см
Hip Room — Third Row	109.982 см
Leg Room — Front	105.664 — 106.172 см
Leg Room — Rear	97. 282 см
Leg Room — Third Row	76.2 см
Shoulder Room — Front	145.034 см
Shoulder Room — Rear	140.462 см
Shoulder Room — Third Row	133.604 см

Габариты салона автомобиля Тойота РАВ4 2009

Высокие водители должны с особым пристрастием проверять габариты салона 2009 Тойота РАВ4, дабы быть уверенными в том, что ничто не помешает получить удовольствие от вождения. К примеру, при достаточной габаритной высоте можно избежать неестественной посадки в водительском кресле, а хорошая ширина салона обеспечит комфортное соседство с пассажиром и вам не придется упираться локтями друг в друга. Важно также проверить достаточно ли в автомобиле места для ног спереди и сзади. Все эти габариты в сумме определяют объем свободного пространства в салоне автомобиля.

Размеры конкурентов

• Размеры Шевроле Эквинокс 2009

• Размеры Шевроле ХХР 2009

• Размеры Субару Форестер 2009

• Размеры Сузуки Гранд Витара 2009

• Размеры Сузуки ХЛ7 2009

• Размеры Фольксваген Тигуан 2009

Размеры модели Тойота РАВ4 по годам

• 2015
• 2014
• 2013
• 2012
• 2011
• 2010
• 2009
• 2008
• 2007
• 2006
• 2005
• 2004
• 2003
• 2002
• 2001
• 2000
• 1999

Другие модели Тойота 2009 года

Шины, диски на Тойота Рав 4 (Toyota Rav 4)

Кроссовер Тойота Рав 4 ежегодно доказывает свою надежность и качество во время движения по дорожному покрытию любой сложности. Курсовая надежность, стабильность, способность к маневренности отличают этот автомобиль из множества. Подчеркивают эти неизменные качества верно подобранные шины и колесные диски.

Какие размеры шин и дисков рекомендуются в KOLOBOX для Toyota Rav 4?

Типоразмер автопокрышек и дисков зависит от года выпуска автомобиля и его модификации. Исходя из перечисленных параметров, в таблице представлены рекомендуемые размеры шин и колесных дисков для Тойота Рав 4.

TOYOTA RAV4 01.01.1994 — 01.06.2000
Шины				Диски
R16
Оригинал	215/70R16
Замена	235/60R16
TOYOTA RAV4 01. 06.2000 — 01.05.2006 II(A2)
Шины				Диски
R16
Оригинал	235/60R16			Оригинал	6.5-7×16 5*114,3 d60-60.1 ET35-45
Оригинал	215/70R16			Замена	6-8×16 5*114,3 d60-100 ET20-45
TOYOTA RAV4 01.05.2006 — 01.01.2013 III(A3)
Шины				Диски
R16
Оригинал	215/70R16			Оригинал	6.5-7×16 5*114,3 d60-60.1 ET45
Замена	235/60R16			Замена	6-8×16 5*114,3 d60-100 ET20-45
R17
Оригинал	225/65R17			Оригинал	7×17 5*114,3 d60-60. 1 ET45
Замена	235/65R17			Замена	6.5-8×17 5*114,3 d60-100 ET20-45
Замена	255/60R17
Замена	245/60R17
R18
Замена	245/55R18			Оригинал	7.5×18 5*114,3 d60-60.1 ET45
Замена	265/50R18			Замена	7.5-9×18 5*114,3 d60-100 ET20-45
Замена	225/60R18
TOYOTA RAV4 01. 01.2013- IV(CA40)
Шины				Диски
R17
Оригинал	225/65R17			Оригинал	7×17 5*114,3 d60-60.1 ET39
				Замена	6-9×17 5*114,3 d60-100 ET20-45
R18
Оригинал	235/55R18			Оригинал	7.5×18 5*114,3 d60-60.1 ET45
Оригинал	225/60R18			Замена	7-9×18 5*114,3 d60-100 ET20-45

Тойота Рав 4, выпускаемая с 2013 года, отпускается заводом-производителем с покрышками размеров: диаметр 17 дюймов, ширина 225 мм, профиль (отношение ширины к высоте колеса) 65%.

Замена возможна на более крупный диаметр: 18 дюймов. Ширина при этом варьируется от 225 до 235 мм, а профиль от 60 до 55% соответственно.

Какая резина подходит для автомобиля Toyota Rav 4 в зимнее время года?

Зимние автомобильные покрышки должны, по возможности, соответствовать техническим характеристикам, указанным в документации к конкретному автомобилю. Объясняется это тем, что водитель и его пассажиры в зимнее время года нуждаются в повышенной степени безопасности, т.к. дорожное покрытие не отличается той надежностью, коей располагало оно летом. Гололедица, припорошенная снегом, несет в себе вероятность заноса при неверном выборе автопокрышек.

В таблице представлены возможные модели зимних комплектов шин для Тойота Рав 4.

Зимние автошины для авто Тойота Рав 4	Pirelli Ice Zero Friction 106T (XL) Maxxis NS5 Premitra Ice Nord 102T Sailun Ice Blazer WST1 102S Cordiant Snow Cross (PW-2) 106T Formula Ice 102T

Вне зависимости от популярных брендов автомобильных покрышек, необходимо определить характер зимы в регионе эксплуатации автомобиля. Если теплая зима предполагает использование фрикционной резины, то для морозной зимы стоит склониться к шипованным покрышкам.

Какие шины подходят для автомобиля Toyota Rav 4 в летнее время года?

Заводская комплектация автомобиля Тойота Рав 4 предполагает следующий размер автопокрышек: 225 мм — ширина, 65% — профиль, 17 дюймов — шина радиальной конструкции.

Замена возможна на 18-ти дюймовые колеса, имеющие ширину в 225 и 235 мм, а профиль в 60 и 55 % соответственно.

Можно обратить внимание на такие бренды автомобильных покрышек: Nokian, Cordiant, Pirelli, Bridgestone, Michelin, Continental. За консультацией в выборе, выделением наиболее популярных моделей с их положительными и отрицательными сторонами водитель может обратиться к специалистам компании KOLOBOX! Все сотрудники этой компании могут предоставить исчерпывающую информацию о подходящих конкретному автомобилю моделях шин.

Какие диски рекомендуются для автомобиля Toyota Rav 4?

Правильный выбор колесных дисков для авто Тойота Рав 4 возможен при знании некоторых рекомендованных размерах:

• Сверловка имеет следующие параметры: пять отверстий, предназначенных для крепления гаек или шурупов, расположенных на окружности диска диаметром 114,3 мм.
• Диаметр крепежной гайки 12 дюймов, а ширина 1,5 дюймов.
• Вылет у заводской комплектации ЕТ 39 или ЕТ 45, возможна замена на ЕТ 40 или ЕТ 45.

Какое давление рекомендуется для шин автомобиля Toyota Rav 4?

Рекомендация завода-производителя заключается в поддержании давления в передних и задних колесах на отметке в 2,2 Атм при диаметре шин радиальной конструкции 17 дюймов, ширине 225 мм и профиле 65%.

Каково влияние размера шин и дисков на характеристики автомобиля?

Рассмотрим влияние в таблице ниже:

Четыре измерения

Четыре измерения

ГЭС 0410

Эйнштейн для всех

---

Назад на страницу основного курса

Джон Д. Нортон
Кафедра истории и философии науки
Университет Питтсбурга

• Одномерный интервал
• Двумерный квадрат
• Трехмерный куб
• Четырехмерный куб: тессеракт
• Стереовидение
• Сводная таблица
• Вместительный вызов
• Запутанный вызов
• Использование цветов для визуализации дополнительного измерения
• Что вы должны знать

Мы уже видели, что нет ничего страшного таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время. Тем не менее трудно устоять перед затянувшимся беспокойство по поводу идеи четырехмерного пространства-времени. проблема не в время часть четырехмерного пространства-времени; это это четыре . Легко представить себе три оси трехмерного мерное пространство: вверх-вниз, поперек и задом наперед. Но куда нам поставить четвертую ось, чтобы сделать четырехмерное пространство?

Моя текущая цель — показать вам, что в все таинственное в четырех измерениях пространства-времени. Для этого я брошу временная часть полностью. Я просто рассмотрю четырехмерный космос; то есть пространство точно такое же, как наше трехмерное пространство, но с одно дополнительное измерение. Каково это?

Без всяких усилий я могу визуализировать трехмерное -мерное пространство — и вы тоже можете. Что бы это быть как жить в трехмерном кубе? Чтобы его попросили визуализировать это как просят дышать или моргать. Это легко. Там мы сидим в куб с шестью квадратными стенками и восемью углами. Наш разум позволяет мы парим внутри.

Могу ли я представить, каково было бы жить в четырехмерный аналог куба, четырехмерный куб или «тессеракт»? Я не могу представить это с таким же легким непосредственность. Сомневаюсь, что и вы сможете. Но это только о единственное, что мы не можем сделать. В противном случае мы можем определить все свойства тессеракта и то, что это будет нравится жить в одном. Для этого существует множество техник. я покажет вам один ниже. Он включает в себя продвижение через последовательность измерений, экстраполируя естественные выводы в каждом шагнуть в четвертое измерение. Как только вы видели, как это делается для особого случая тессеракта у вас не будет проблем применяя его к другим случаям.

Дверь в четвертое измерение открывается.

Одномерный интервал

Одномерным аналогом куба является интервал. Это формируется путем взятия безразмерной точки и ее перетаскивания на определенное расстояние. Это расстояние может быть 2 дюйма или 3 фута или что-то еще. Давайте позвоним расстояние «Л».

Интервал имеет длину L. Он ограничен двумя точками как его грани — две точки на обоих концах интервала.

Двумерный квадрат

Двумерным аналогом куба является квадрат. Это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.

Квадрат имеет площадь L ² . Он ограничен гранями на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре. их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.

Итак, у нас есть 2 измерения x 2 грани в каждой = 4 грани. грани вместе образуют периметр длиной 4xL.

Трехмерный куб

Чтобы сформировать куб, мы берем квадрат и перетаскиваем его на расстояние L в третьем измерении.

Объем куба L ³ . Он ограничен гранями на 6 сторон. Грани представляют собой квадраты площадью L ² . Мы знаем, что есть 6 из них, так как его трехмерные оси должны быть закрыты с обоих концов лица.

Итак, у нас есть 3 измерения x 2 грани в каждой = 6 граней. грани вместе образуют поверхность площадью 6xL ² . Рисование изображение трехмерного куба на двумерной поверхности одинаково легко. Берем две его грани — два квадрата — и соединяем углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами. На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.

Четырехмерный куб: тессеракт

Пока я надеюсь, что вы нашли наши конструкции полностью безупречный. Следующий шаг в четыре измерения можно сделать одинаково механически. Мы просто систематически повторяем каждый шаг выше. Единственный разница в том, что на этот раз мы не можем легко сформировать ментальную картину что мы строим. Но мы можем знать все его свойства!

Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его расстояние L в четвертом измерении . Мы не можем точно представить как это выглядит, но это примерно так:

Тессеракт имеет объем L ⁴ . Он ограничен лица с 8 сторон. Грани представляют собой кубы объема L ³ . Мы знаем их 8, так как его четыре оси должны быть ограничены любой конец гранями — две кубические грани на ось. Еще раз, мы не можем визуализируйте все четыре из этих закрытых измерений. Мы можем в лучшем случае визуализировать три направления перпендикулярны друг другу. Затем мы каким-то образом добавим в четвертый (красный):

Итак, у нас есть 4 измерения по 2 грани в каждой = 8 граней. грани вместе образуют «поверхность» (на самом деле трехмерный объем) размером 8xL ³ в объеме. Рисование изображения четырехмерного тессеракта в трехмерном размерное пространство прямолинейно. Мы берем два его лица — два кубики — и соедините углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на тессеракт под разными углами. Фигура показывает два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.

Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL ³ ).

Стереовидение

«Чертежи» тессеракта плохо видны. Это потому, что они действительно должны быть трехмерными моделями в трехмерное пространство. Итак, что у нас есть выше, это два объемный чертежи трехмерных моделей четырехмерного тессеракт. Неудивительно, что он становится грязным!

Изображения ниже представляют собой стереопары. Если вы знакомы с тем, как их просматривать, вы увидите, что они дают вам хороший стереофонический вид трехмерной модели. Если это новое для вас, они берут практика, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не смотрит на левое изображение и правый глаз смотрит на правое изображение.

Но как научиться этому? мне проще всего начать, если я сижу далеко от экрана и смотрю вдаль над верхней частью экрана. Я вижу два несколько размытых изображения на край моего поля зрения. Пока я не сосредотачиваюсь на них, они начинают дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют вместе тем лучше. Я стараюсь усилить дрейф, насколько это возможно, пока осторожно перемещая свой взгляд к изображениям. Цель состоит в том, чтобы получить два изображения для слияния. Когда они это делают, я продолжаю смотреть на объединенные изображения, улучшается фокусировка и появляется полный трехмерный стереоэффект резко. Эффект поразителен и стоит небольших усилий.

Эту пару легче сплавить:

и этот немного сложнее:

Сводная таблица

Мы можем подытожить развитие свойств tesseract следующим образом:

Размер	Фигурка	Лицо	Том	Номер лиц	Том поверхность/периметр
1	интервал	точка	л	1×2=2	два очки
2	квадрат	интервал	л 2	2×2=4	4 л
3	куб	квадрат	л 3	3×2=6	6 л 2
4	тессеракт	куб	л 4	4×2=8	8 л 3

Вместительный вызов

Если бы вы жили в тессеракте, вы могли бы выбрать жить на своей трехмерной поверхности, как двухмерный человек могли бы выбрать жить в 6 квадратных комнатах, которые образуют двухмерный поверхность куба.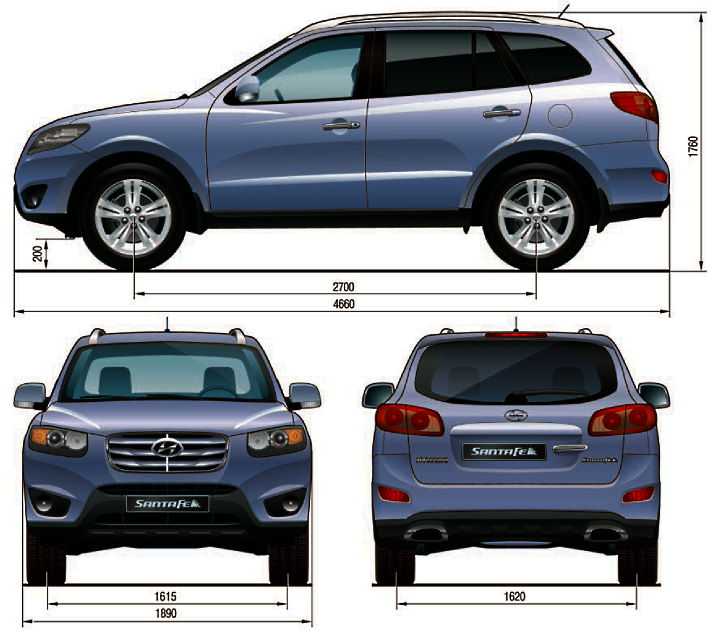 Таким образом, ваш дом будет состоять из восьми кубов, образующих поверхность. из тессеракта. Представьте себе, что есть двери, где когда-либо две из эти кубики встречаются. Если вы находитесь в одной из этих комнат, сколько дверей будет Понимаете? Как бы выглядела следующая комната, если бы вы прошли через одну из двери? Через сколько дверей нужно пройти, чтобы добраться до самой дальней комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо окна снаружи тессеракта? Как насчет окон внутрь? тессеракт?

Некоторые из этих вопросов непростые. Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы на тессеракт.

Запутанный вызов

Доступ к четвертому измерению делает возможным многое иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать стратегия обдумывания процесса в трехмерном пространстве. Затем мы воспроизвели его в четырехмерном пространстве.

Рассмотрим монету, лежащую в рамке на столе.

Монета не может быть удалена из рамки в пределах ограничивает двумерную поверхность стола. Теперь вспомните что у нас есть доступ к третьему измерению. Монета легко удалить, просто подняв его в третье измерение, высота над столом. После этого мы можем передвигать монету по своему усмотрению в более высокую слой, а затем опуститься обратно на столешницу за пределами рамы.

При подъеме следует обратить внимание на то, что движение вообще не двигает монету в двух горизонтальных направлениях двух объемное пространство. Таким образом, движение никогда не приближает его к кадру и там нет опасности столкновения с рамой.

Теперь повторите этот анализ для его аналог в одном более высоком измерении, мрамор запертым в трехмерном ящике.

Мрамор можно удалить в точно так же, «подняв» его, на этот раз в четвертое измерение. Как и монета в рамке, ключ следует отметить, что при этом подъемном движении шарик положение в трех пространственных направлениях ящика без изменений. Мрамор никогда не приближается стены и нет опасности столкновения с ними. Как только оно поднимается в новое трехмерное пространство, оно можно свободно перемещать в этом пространстве и опускать обратно в исходное трехмерное пространство, но теперь за пределы коробка.

Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве. Можем мы разделить их, используя доступ к четвертому измерению?

Это можно сделать точно так же процесс подъема одного из колец в четвертое измерение. Как прежде обратите внимание, что подъем не перемещает кольцо ни в одном из три направления трехмерного пространства, удерживающие первоначально связанные кольца. Так что движения рисков нет столкновения перемещаемого кольца с другим. Подъем просто поднимает перемещенное кольцо на новый трехмерный слой из четырех размерное пространство, в котором нет ни одной части другого кольца. перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы с удовольствием опустился обратно в исходное трехмерное пространство в совсем другое место.

А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке. Некоторые узлы просто кажущиеся клубки, которые могут довольно легко разойтись. Остальные настоящие и можно расстегнуть, только продев конец веревки в петлю. Так примите это за настоящий узел: тот, который не может быть развязаны любыми манипуляциями с веревкой, если мы не сможем ухватиться за заканчивается. (Представьте, если хотите, что каждый из них прикреплен к стене и нельзя удалить.)

Задача состоит в том, чтобы убедить сами понимаете, что в четырехмерном пространстве на веревках нет настоящих узлов. космос. Основная помощь, которая вам понадобится, — это описанная выше манипуляция с связанные кольца.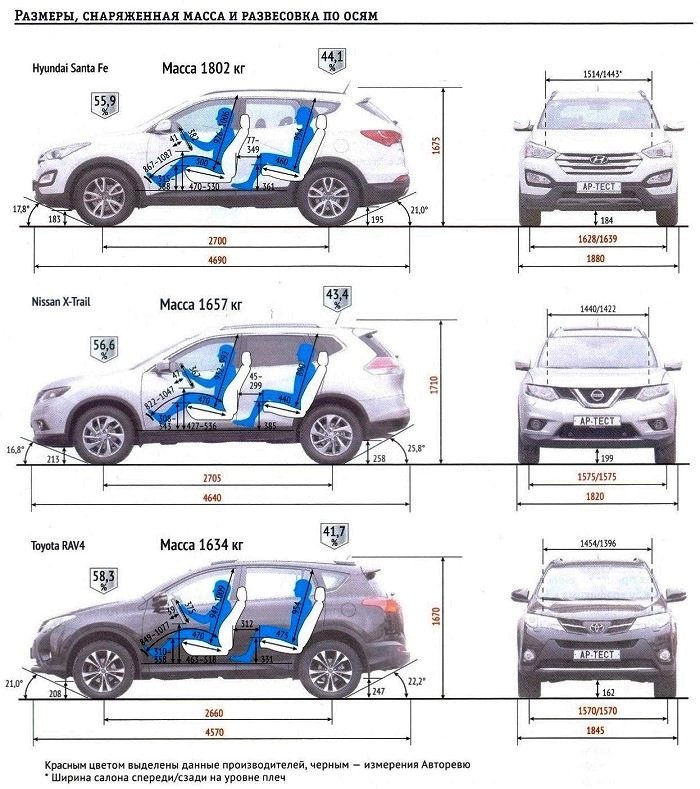 Для начала представьте, как бы вы использовали четвертый измерение, чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.

Использование цветов для визуализации дополнительных размер

Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства может быть представлено различия цветов.

Вот как это работает, когда мы начинаем с двухмерного пространства и подняться в третье измерение. Объекты в оригинале два мерное пространство черное. Когда мы поднимаемся через третий измерения, они последовательно приобретают синий цвет, зеленый и красный.

Теперь давайте применим этот цветной слой.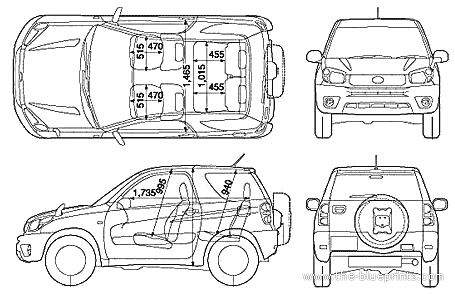 трюк к более раннему примеру подъема монеты из рамки. монета начинается в том же двухмерном пространстве, что и рамка. Мы поднимаем это в третье измерение в более высокое пространственный слой, который мы закодировали красным цветом. В этом высшем слой, монета может свободно перемещаться влево/вправо и вперед/назад без пересекающие рамку. Мы перемещаем его вправо, пока он не пройдет над рамой. Затем опускаем обратно вниз снаружи.

А теперь представьте, что мы не можем воспринимать третье измерение напрямую. Вот как мы представить побег монеты. Он начинается внутри кадра в пространство кадра. Затем он поднимается из рамы в третье измерение. В этот момент на это указывает призрачный красная монета. Его пространственное положение слева/справа и направление вперед/назад не изменилось. Все, что изменилось, это его высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево или справа, или спереди и сзади, в этом красном слое уже не пересекает рамку и может двигаться прямо над ней. мы этого не увидим однако перемещайтесь по кадру. Насколько нам известно, это будет просто пройди через это. Движение монеты в этом трехмерном побеге иллюстрируется призрачным красным монета.

Этот последний анализ монеты в кадр является шаблоном для работы с реальный случай шарика, заключенного в трехмерную коробку. Если шарик движется в любом из трех известных измерений (вверх/вниз, влево/вправо и вперед/назад), его движение пересекает стены ящик, и он не может убежать. Итак, мы поднимаем шарик в четвертый измерение, не меняя своего положения в трех привычных размеры.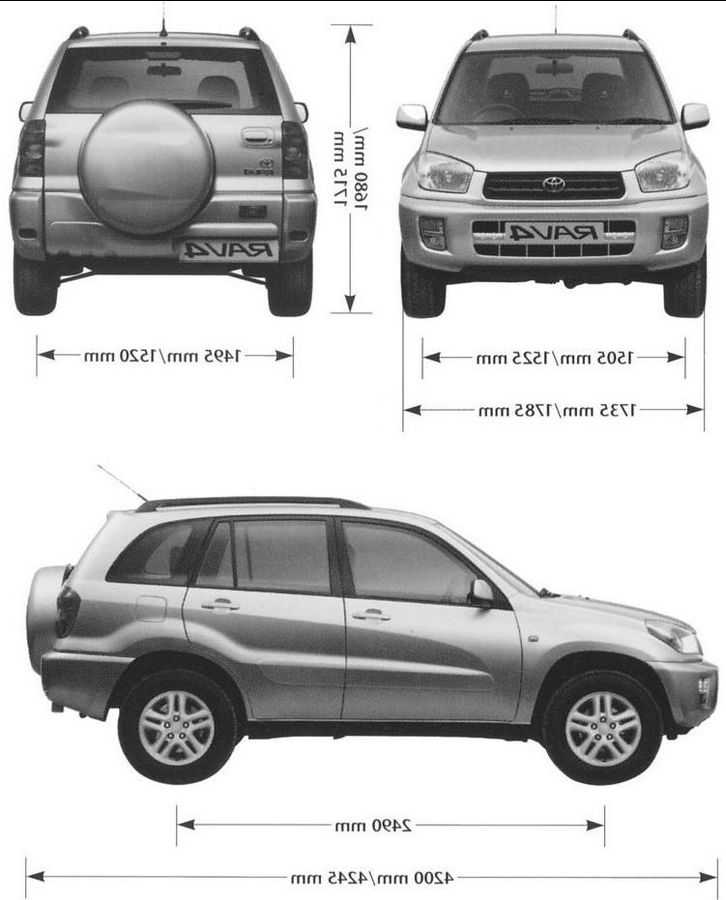 На рисунке это показано тем, что мрамор становится призрачным. красный. В красном поле шарик может двигаться вверх/вниз, слева/справа и спереди/сзади, не пересекая стенки коробки. Затем мрамор перемещается так, что проходит над одной из стен. Это затем опустили из красного пространства обратно к исходным трем мерное пространство коробки, но уже вне стен.

То же анализ относится к связанным кольцам. Одно кольцо снято из трехмерного пространства исходной установки. В этом красное пространство, кольцо может свободно двигаться, не пересекаясь с другим кольцо. Мы отодвигаем его подальше от другого кольца, а затем опускаем обратно. в исходное трехмерное пространство. Теперь он не связан с другое кольцо.

Что следует знать

• Свойства квадратов, кубов и тессерактов.
• Как получить свойства тессеракта и других четырехмерные фигуры путем экстраполяции методов, используемых для получения свойства куба.

Авторское право Джон Д. Нортон. февраль 2001 г.; июль 2006 г., 2 февраля 2008 г.; 6 февраля 2012 г.; 30 апреля 2014. Январь 30, 2022.

Визуализация четвертого измерения — исследовательский блог

Живя в трехмерном мире, мы можем легко визуализировать объекты в двух и трех измерениях. Но как математик, игра только с тремя измерениями ограничивает, сетует доктор Генри Сегерман. Доцент кафедры математики в Университете штата Оклахома, Сегерман говорил со студентами и преподавателями Дьюка о визуализации 4-мерного пространства в рамках серии лекций PLUM 18 апреля.

Что такое 4-е измерение?

Давайте разложим пространственные измерения на то, что мы знаем. Мы можем описать точку в 2-мерном пространстве двумя числами x и y , визуализируя объект в плоскости xy , и точку в 3D пространстве 3 числами в системе координат xyz .

Построение трехмерного изображения в системе координат xyz  .

Хотя зеленые маркеры прямого угла на самом деле не равны 90 градусам, мы можем сделать вывод о трехмерной геометрии, как показано на двухмерном экране.

Точно так же мы можем описать точку в 4-мерном пространстве четырьмя числами — x , y , z и w — где фиолетовая ось w- проходит под прямым углом к другие регионы; другими словами, мы можем визуализировать 4 измерения, сжав их до трех.

Построение четырехмерного изображения в системе координат xyzw .

Один из часто исследуемых четырехмерных объектов, которые мы можем попытаться визуализировать, известен как гиперкуб. Гиперкуб аналогичен кубу в трех измерениях, точно так же, как куб — ​​квадрату.

Как сделать гиперкуб?

Чтобы создать 1D-линию, мы берем точку, делаем копию, перемещаем скопированную точку параллельно на некоторое расстояние, а затем соединяем две точки линией.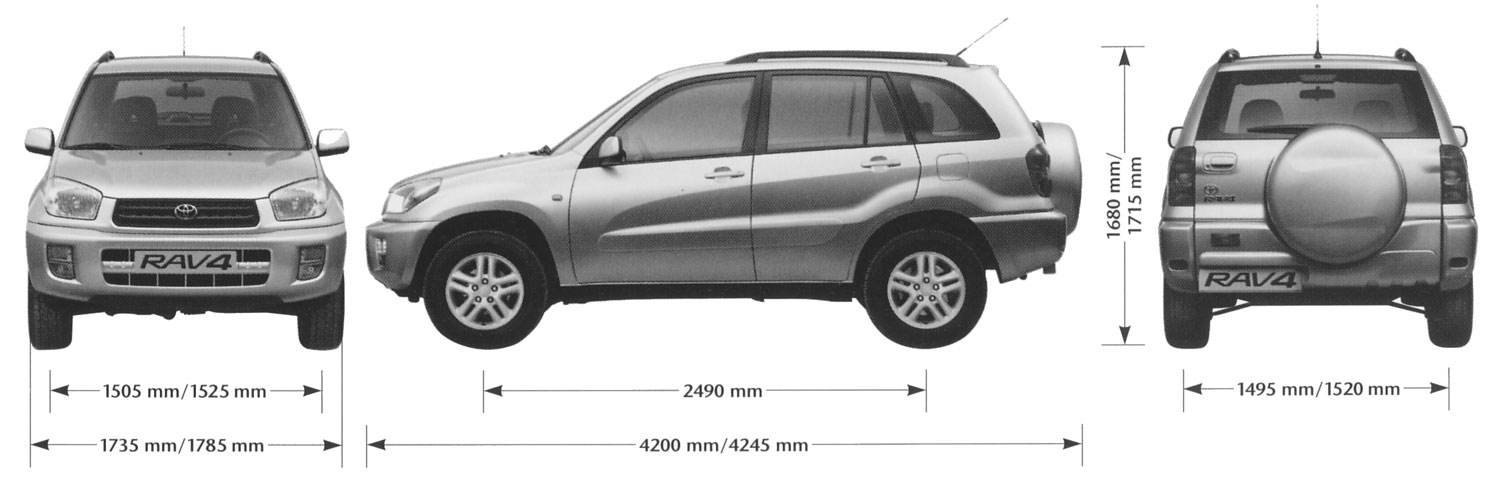

Точно так же можно сформировать квадрат, сделав копию линии и соединив их, чтобы добавить второе измерение.

Итак, чтобы создать гиперкуб, мы перемещаем одинаковые 3D-кубы параллельно друг другу, а затем соединяем их четырьмя линиями, как показано на изображении ниже.

Для создания n -мерного куба возьмем 2 копии ( n −1)-мерного куба и соединим соответствующие углы.

Даже с 3D-моделью попытка визуализировать гиперкуб может привести к путанице.

Изображение возможного гиперкуба Батшебой Гроссман.

Как мы можем улучшить изображение гиперкуба? «Вы вроде жульничаете, — объяснил доктор Сегерман. Один из способов обмана — отбрасывание теней.

Параллельные проекционные тени, изображенные на рисунке ниже, вызваны лучами света, падающими под прямым углом к ​​плоскости стола. Мы видим, что некоторые края тени параллельны, что верно и для физического объекта. Однако некоторые ребра, которые сталкиваются в 2D-слепке, на самом деле не сталкиваются в 3D-объекте, что усложняет сопоставление проекции с 3D-объектом.

Параллельная проекция куба на прозрачный пластиковый лист над столом.

Один из способов отбрасывать тени без столкновений — использовать стереографическую проекцию, как показано ниже.

Стереографическая проекция — это отображение (функция), которое проецирует сферу на плоскость. Проекция определена на всей сфере, за исключением точки в верхней части сферы.

Для объекта ниже кривые на сфере отбрасывают тени, сопоставляя их с сеткой прямых линий на плоскости. При стереографической проекции каждая сторона 3D-объекта сопоставляется с другой точкой на плоскости, поэтому мы можем видеть все стороны исходного объекта.

Стереографическая проекция сетки на плоскость. Распечатайте модель на 3D-принтере в Duke’s Co-Lab!

Так же, как тени 3D-объектов представляют собой изображения, сформированные на 2D-поверхности, наша сетчатка имеет только площадь 2D-поверхности для обнаружения света, попадающего в глаз, поэтому мы фактически видим 2D-проекцию нашего 3D-мира.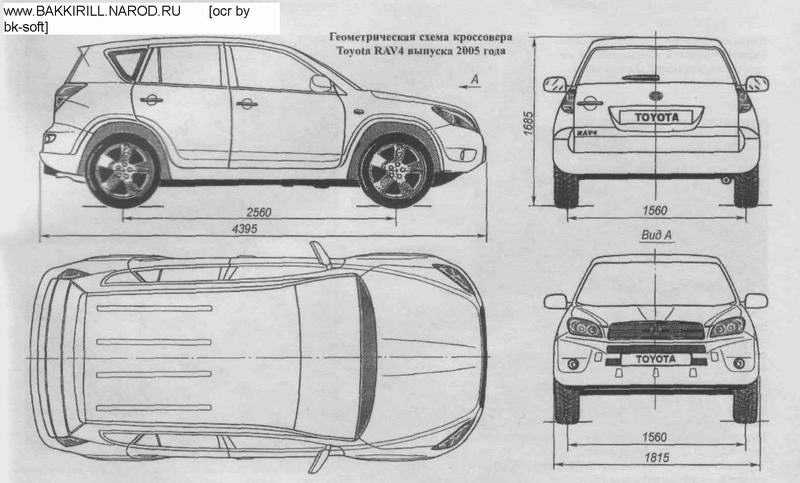 Наш разум способен с помощью вычислений реконструировать трехмерный мир вокруг нас, используя предыдущий опыт и информацию из двухмерных изображений, такую ​​как свет, тень и параллакс.

Проекция 3D-объекта на 2D-поверхность.

Проекция четырехмерного объекта на трехмерный мир

Как мы можем визуализировать четырехмерный гиперкуб?

Чтобы использовать стереографическую проекцию, мы радиально проецируем края трехмерного куба (слева на изображении ниже) на поверхность сферы, чтобы сформировать «куб для пляжного мяча» (справа).

Грани куба радиально проецируются на сферу.

Поместив точечный источник света на северный полюс раздутого куба, мы можем получить проекцию на 2D-плоскость, как показано ниже.

Стереографическая проекция рисунка «кубик пляжного мяча» на плоскость. Посмотреть 3D-модель здесь.

Применительно к одному измерению выше, мы теоретически можем взорвать 4-мерную фигуру в шар, а затем поместить свет в верхнюю часть объекта и проецировать изображение вниз в 3 измерения.

Слева : 3D-печать стереографической проекции «гиперкуба с надувным мячом» на трехмерное пространство. Справа : компьютерная визуализация того же, включая 2-мерные квадратные грани.

Формирование n –мерных кубов из ( n −1)–мерных визуализаций.

Таким образом, построенная трехмерная модель тени «кубика пляжного мяча» является проекцией гиперкуба в трехмерное пространство. Здесь 4-мерные ребра гиперкуба становятся искаженными кубами вместо полос.

Точно так же, как края верхнего объекта на рисунке можно соединить вместе, сложив квадраты в 3-м измерении, чтобы сформировать куб, края нижнего объекта можно соединить в 4-м измерении

Почему мы пытаемся понять вещи в четырех измерениях?

Насколько нам известно, пространство вокруг нас состоит только из 3-х измерений. Однако с математической точки зрения нет причин ограничивать наше понимание многомерной геометрии и пространства только тремя, поскольку в числе 3 нет ничего особенного, что делает его единственным возможным числом измерений, которое может иметь пространство.