Определение коэффициента лобового сопротивления самолета.

Коэффициент лобового сопротивления компоновки самолета, симметричного относительно плоскости X0Z () при углах атакидля самолета с крылом малого удлинения,для самолета с крылом большого удлинения, определяется как сумма коэффициентов лобового сопротивления при нулевой подъемной силе -и индуктивного сопротивления: .

Коэффициент рассчитывается по формуле:

— коэффициенты лобового сопротивления с учетом интерференции фюзеляжа с крылом, горизонтальным и вертикальным оперениями;

-коэффициент, учитывающий дополнительное сопротивление, обусловленное технологическими неровностями поверхности (стыковочные узлы, люки, царапины) , = 0.003 …0.004 ;

К – поправочный коэффициент, уточняющий формулу на неучтенные факторы,

К =1.05 …1.1.

— коэффициент индуктивного сопротивления самолета,

где А – коэффициент отвала поляры,

— коэффициент подъемной силы самолета.

Определение коэффициента лобового сопротивления фюзеляжа при нулевой подъемной силе.

Коэффициент лобового сопротивления фюзеляжа самолета при нулевой подъемной силе отличается от соответствующего коэффициента изолированного фюзеляжаувеличением донного сопротивления в диапазоне чисел Маха, что учитывается при расчете коэффициента донного сопротивления фюзеляжа

Расчет коэффициента лобового сопротивления изолированного фюзеляжа при нулевой подъемной силе выполняется по соотношению:

где — коэффициент лобового сопротивления трения,

— коэффициент лобового сопротивления давления.

Коэффициент лобового сопротивления трения определяется по формуле:

где — коэффициент сопротивления трения плоской пластины в несжимаемом потоке для полностью турбулентного пограничного слоя,

— число Рейнольдса, рассчитанное по длине фюзеляжа ,

— коэффициент, учитывающий влияние сжимаемости (снимается с графика),

— коэффициент формы, учитывающий отличие фюзеляжа от плоской пластины (снимается с графика),

— площадь омываемой поверхности фюзеляжа (боковой, без площади поверхности донного среза),

— кинематический коэффициент вязкости, определяемый по таблице стандартной атмосферы в зависимости от высоты полета.

фюз
К	1,05
xt	0,5
Fф	64,45919807
Sбокнос	9,124755862
Sбокцил	47,10346945
Sбоккорм	8,230972752

M∞	0,6	0,7	0,8	1,6	1,8	2
Reф	6,93E+07	8,08E+07	9,24E+07	1,85E+08	2,08E+08	2,31E+08
V∞	179,7192	209,6724	239,6256	479,2512	539,1576	599,064
2Cf	0,003	0,0025	0,0024	0,0023	0,0022	0,0021
ημ	0,98	0,96	0,95	0,9	0,82	0,8
ηλ	1,08
Cxa0фтр	0,052861174	0,043152	0,04099438	0,037218582	0,032435904	0,030206

Коэффициент сопротивления давления определяется по формуле:

где — соответственно коэффициенты сопротивления носовой и кормовой частей, донного сопротивления.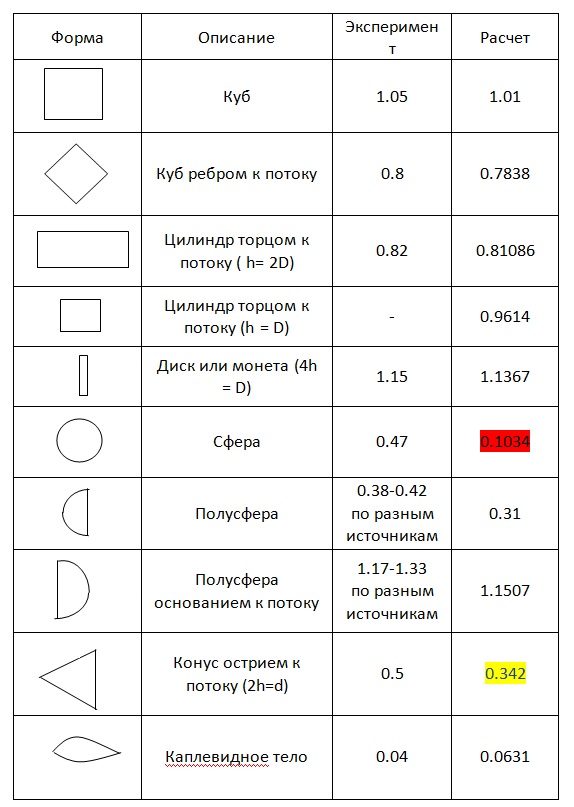

Коэффициент сопротивления носовой частиопределяется по графикам в зависимости от числа Маха и.

Коэффициент сопротивления кормовой части фюзеляжа форма обводов кормовой части), определяется по графику Коэффициент сопротивления донного среза при неработающем двигателе определяется для всех значений числаМ_ по формуле:

,

где – площадь донного среза,- диаметр донного среза,– коэффициент донного давления.

При М_< 0.8 ,

— коэффициент, учитывающий влияние удлинения и сужения кормовой части, — коэффициент трения плоской пластины, определяемый по числу.

При М>0.8 определяется по графикам в зависимости от числа Маха, коэффициенттакже снимается по графикам.

M∞	0,6	0,7	0,8	1,6	1,8	2
√(M-1)/λнос	0,428668942	0,3826636	0,321501706	0,669259171	0,801966157	ё
(Cханос)при ϕ=1	0	0	0	0,104798949	0,074651306	0,068909
Cхакорм	0,045	0,045	0,06	0,075	0,065	0,051

Коэффициент сопротивления донного среза фюзеляжа:

M∞	0,6	0,7	0,8	1,6	1,8	2
1-ηкорм	0,21853068
Kη	0,18	0,18	0,18	0,42	0,5	0,55
Cр дон	-0,3233	-0,3542	-0,3615	-0,28	-0,27	-0,2
Cxдон	0,026020793	0,0285044	0,029092131	0,052573439	0,060352163	0,049176
Cxaфдавл	0,07102079	0,073504	0,08909213	0,23237239	0,20000347	0,16908

Cxa0ф

0,123881967

0,1166563

0,13008651

0,26959097

0,232439373

0,199291

Расчет коэффициента лобового сопротивления несущей поверхности (крыла, ГО, ВО) при нулевой подъемной силе.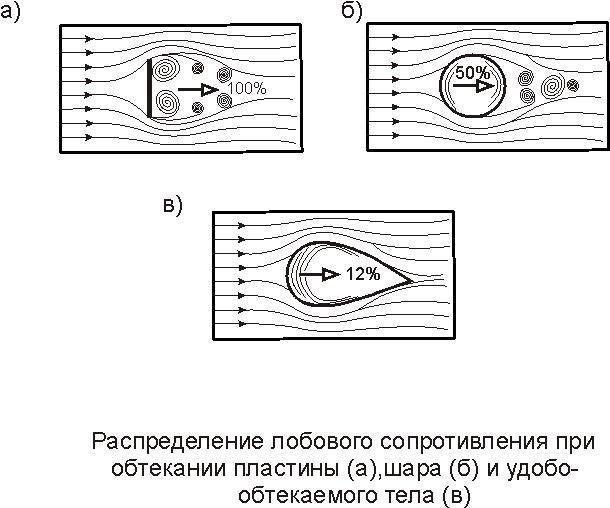

Коэффициент лобового сопротивления изолированной несущей поверхности при нулевой подъемной силе определяется по формуле:

где — коэффициент профильного сопротивления, состоящий из сопротивления трения и сопротивления давления, обусловленного перераспределением давления из-за влияния вязкости;- коэффициент волнового сопротивления, обусловленный потерями полного давления (потерями энергии) в скачках уплотнения и перераспределением давления на сверхзвуковых скоростях.

Коэффициент профильного сопротивления:

(4.13)

где — коэффициент, учитывающий долю несущей поверхности= 2.

— коэффициент, учитывающий влияние на профильное сопротивление толщины профиля снимается с графика ,

— коэффициент, учитывающий влияние числа Маха берется с графика.

Коэффициент трения плоской пластины (верхняя и нижняя поверхность) определяется по графику .

Число Рейнольдса для рассматриваемой несущей поверхности ,- средняя аэродинамическая хорда консольной части несущей поверхности (крыла, ГО, ВО). Как и в случае расчета коэффициента сопротивления трения фюзеляжа, для несущей поверхности принимаем пограничный слой турбулентным. Некоторое завышение коэффициента сопротивления допускается, что определяет запас тяги двигателя.

Крыло

M∞	0,6	0,7	0,8	1,6	1,8	2
Reф	6,93E+07	8,08E+07	9,24E+07	1,85E+08	2,08E+08	2,31E+08
V∞	179,7192	209,6724	239,6256	479,2512	539,1576	599,064
Cf	0,0015	0,00125	0,0012	0,00115	0,0011	0,00105
Cхар	0,00304584	0,0025382	0,002436672	0,002335144	0,002233616	0,002132

Вертикальное оперение

M∞	0,6	0,7	0,8	1,6	1,8	2
Reф	6,93E+07	8,08E+07	9,24E+07	1,85E+08	2,08E+08	2,31E+08
V∞	179,7192	209,6724	239,6256	479,2512	539,1576	599,064
Cf	0,0015	0,0015	0,0015	0,0011	0,001	0,001
Cхар	0,003046	0,00304584	0,00304584	0,002233616	0,002031	0,002031

Горизонтальное оперение

M∞	0,6	0,7	0,8	1,6	1,8	2
Reф	6,93E+07	8,08E+07	9,24E+07	1,85E+08	2,08E+08	2,31E+08
V∞	179,7192	209,6724	239,6256	479,2512	539,1576	599,064
Cf	0,0015	0,0015	0,0015	0,0011	0,001	0,001
Cхар	0,003046	0,003046	0,003046	0,002234	0,002031	0,002031

Коэффициент волнового сопротивления несущей поверхности определяется по соотношению

где — коэффициент волнового сопротивления несущей поверхности с ромбовидным профилем.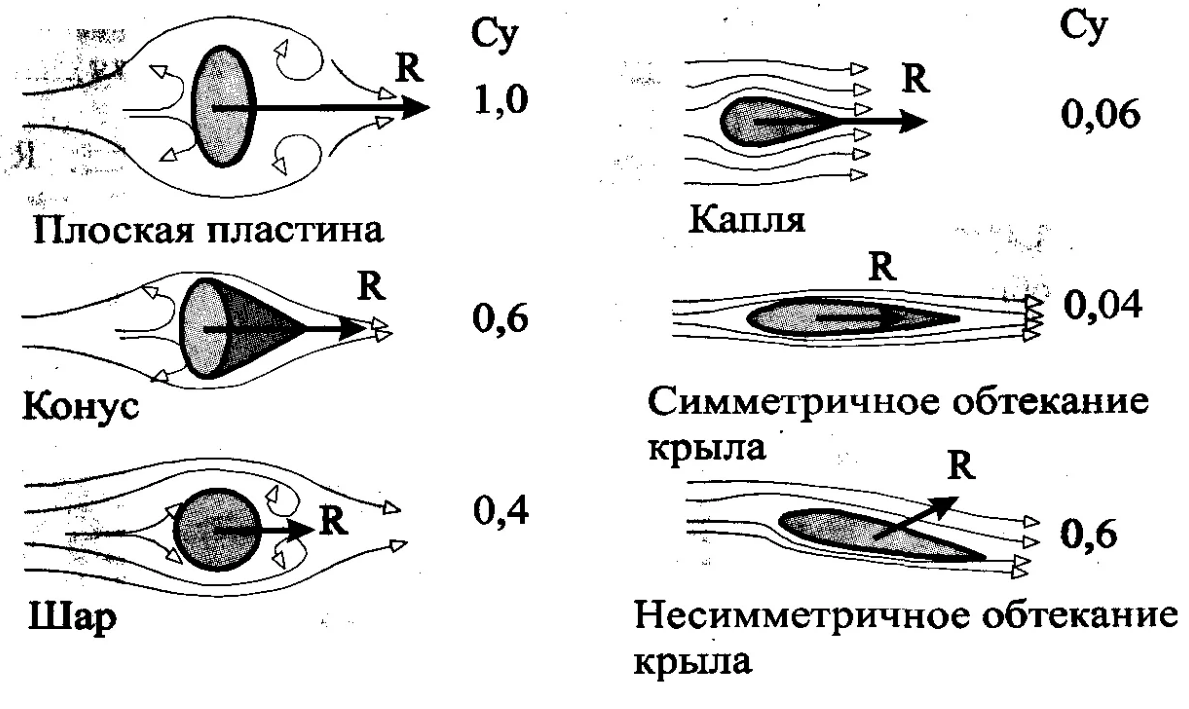 Зависимостипредставлены на графиках и позволяют определить коэффициент.

Коэффициенты, учитывающие влияние на волновое сопротивление формы профиля крыла бесконечного размаха –К,(так как форма профиля — синусоидальная), конечного размаха крыла — снимается с графика и зависит от .

Для ориентировочной оценки коэффициента волнового сопротивления крыла сложной формы в плане исходное крыло разбивают на 2 вспомогательных простых крыла с постоянной стреловидностью по передней кромкеи площадью в плане. Коэффициент волнового сопротивления рассчитывается по формуле

где — коэффициент волнового сопротивленияn-го вспомогательного простого крыла,

K -коэффициент, учитывающий влияние интерференции на волновое сопротивление крыла. В приближенных расчетах можно принять K = 1.15…1.2.

Коэффициент волнового сопротивления крыла:

	1,6	1,8	2
Cxaвлромб	0,0297216	0,02575872	0,024343
Cxaвл	0,0297216	0,033057024	0,025804

Коэффициент волнового сопротивления ВО:

	1,6	1,8	2
Cxaвлромб	0,022722812	0,016896	0,013983
Cxaвл	0,022874297	0,021402	0,018644

Коэффициент волнового сопротивления ГО:

	1,6	1,8	2
Cxaвлромб	0,022723	0,016896	0,013983
Cxaвл	0,022874	0,021402	0,018644

Сха0

0,01704802

0,01583

0,01726748

0,03278182

0,02846074

0,02463

Определение коэффициента индуктивного сопротивления самолета

Коэффициент индуктивного сопротивления самолета определяется соотношением

где А — коэффициент отвала поляры первого рода,

— коэффициент подъемной силы самолета.

В пределах линейной зависимости коэффициент,

где — производная коэффициента подъемной силы по углу атаки.

Тогда ,

где при заданном значении произведение.

Отвал поляры при отсутствии подсасывающей силы для всех чисел Маха определяется:

, где

	0,6	0,7	0,8	1,6	1,8	2
А	0,39808507	0,3763637	0,362863317	0,469079925	0,435848765	0,487484
Kmax	6,069390174	6,4776973	6,316608962	4,032088346	4,489303768	4,562783

	M∞	0,6	0,7	0,8	1,6	1,8	2
α	Сxai
0	0	0	0	0	0	0	0
2		0,003060827	0,00323748	0,00335793	0,002598	0,002796	0,0025
4		0,012243309	0,012949918	0,013431721	0,01039	0,011182	0,009998
6		0,027547446	0,029137316	0,030221371	0,023378	0,025161	0,022496
8		0,048973238	0,051799673	0,053726883	0,041561	0,04473	0,039992

Коэффициент — лобовое сопротивление — цилиндр

Cтраница 1

Сопротивление цилиндра с накладками.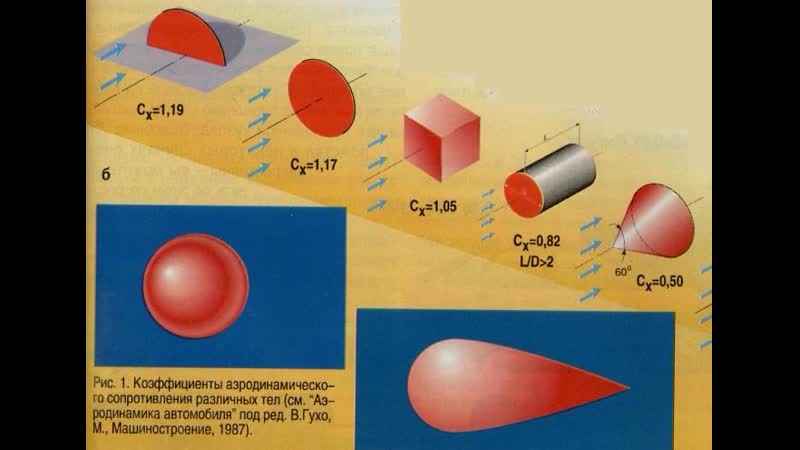  [1]

Коэффициент лобового сопротивления цилиндров треугольного и полукруглого сечений ( А, 8; Re 90000) изменяется при противоположных направлениях потока приблизительно в два раза.  [2]

Вообще коэффициент лобового сопротивления цилиндра зависит не только от числа Рейнольдса и шероховатости поверхности, но и от начальной турбулентности потока.  [3]

Влияние удлинения цилиндров на их лобовое сопротивление.| Коэффициент лобс-вого сопротивления квадратного цилиндра в зависимости от угла атаки.  [4]

На рис. 3.27 приведены опытные значения коэффициента лобового сопротивления квадратного цилиндра ( призмы) бесконечной длины и с удлинением А, 5 в зависимости от угла атаки. Как видно на рис. 3.27, у длинного цилиндра минимум значения коэффициента сх наступает при угле атаки а. Характерно, что наибольшая нагрузка на квадратную сплошностенчатую башню будет при действии ветра по диагонали ( а 45), так как ее наветренная площадь возросла в 1 41 раза, а значение сх снизилось лишь в 1 3 раза.  [5]

График функции.| График функции.  [6]

Эта информация была положена в основу интерполирования коэффициентов лобового сопротивления цилиндра по двум переменным — относительному удлинению и углу атаки. Для интерполирования по удлинению г были использованы интерполяционные полиномы Лагранжа, а по углу атаки — стандартная процедура линейной интерполяции.  [7]

Поскольку можно рассчитывать лишь на таблично заданную зависимость коэффициента лобового сопротивления цилиндра от угла атаки и относительного удлинения, то необходимость проведения соответствующего вычислительного эксперимента очевидна. В справочнике [37] и монографии [11] приведены сводные данные по коэффициентам лобового сопротивления цилиндров с относительными удлинениями из широкого ( по мнению ее автора) диапазона. Эти данные касаются цилиндров с образующей перпендикулярной либо параллельной потоку. В принятой в данной работе терминологии, первый случай соответствует движению цилиндра с углом атаки а — тг / 2, а второй движению с нулевым углом атаки.  [8]

На рис. 12.15 изображена рассчитанная по формуле ( 117) зависимость коэффициента лобового сопротивления цилиндра от числа s C / cm при свободно-молекулярном его обтекании гелием. Для сравнения на этом графике приведены также экспериментальные точки, полученные Штальдером, Гудвином и Кригером1) в аэродинамической трубе.  [9]

Характер обтекания цилиндра приближается к полному обтеканию, и, несмотря на увеличение сил трения, коэффициент лобового сопротивления цилиндра резко падает, так как область разрежения значительно сузилась. Круглый цилиндр а закритической области как бы приближается к хорошо обтекаемым телам, что весьма важно для проектирования строительных конструкций.  [10]

При углах скольжения 3 0 лобовое сопротивление таких цилиндров с ростом этого угла снижается не так сильно, как круглого цилиндра. Коэффициент лобового сопротивления немного скругленных цилиндров при углах 3 0 следует скорее закону сопротивления плоской пластинки.  [11]

Поскольку можно рассчитывать лишь на таблично заданную зависимость коэффициента лобового сопротивления цилиндра от угла атаки и относительного удлинения, то необходимость проведения соответствующего вычислительного эксперимента очевидна. В справочнике [37] и монографии [11] приведены сводные данные по коэффициентам лобового сопротивления цилиндров с относительными удлинениями из широкого ( по мнению ее автора) диапазона. Эти данные касаются цилиндров с образующей перпендикулярной либо параллельной потоку. В принятой в данной работе терминологии, первый случай соответствует движению цилиндра с углом атаки а — тг / 2, а второй движению с нулевым углом атаки.  [12]

Страницы:      1

Эффекты формы при перетаскивании

Эффекты формы при перетаскивании

Коэффициент аэродинамического сопротивления — это число, которое аэродинамики используют для моделирования всех сложных зависимостей перетаскивание по наклону формы, и некоторые условия течения. Коэффициент лобового сопротивления (Cd) равен лобовому сопротивлению (D), деленному на количество: плотность (r), умноженная на контрольную площадь (A), умноженная на половину скорость (V) в квадрате. Этот слайд показывает некоторые типичные значения коэффициента лобового сопротивления для различных форм. Показанные здесь значения были определены экспериментально путем размещения моделей в аэродинамической трубе и измерения величина сопротивления и туннельные условия скорости и плотности. уравнение сопротивления затем использовался для получения коэффициента. Прогнозируемая фронтальная площадь каждого объекта использовалась в качестве эталонной площади. Плоская пластина имеет Cd = 1,28, клиновидная призма с клином обращена вниз по течению имеет Cd = 1,14, сфера имеет Cd, который варьируется от 0,07 до 0,5, пуля Cd = 0,295, а типичный аэродинамический профиль Cd = 0,045.

Мы можем изучить влияние формы на сопротивление, сравнив значения коэффициента сопротивления для любых двух объектов, пока одна и та же ссылка используется площадь, а число Маха и число Рейнольдса совпадают. Все коэффициенты лобового сопротивления на этом слайде были получены на низкой скорости. (дозвуковые) аэродинамические трубы и при аналогичных числах Рейнольдса, за исключением случаев, когда отмеченный. Быстрое сравнение показывает, что плоская пластина дает самые высокие сопротивление, а обтекаемый симметричный аэродинамический профиль обеспечивает наименьшее сопротивление на коэффициент почти 30! Форма очень сильно влияет на количество произведено сопротивление. Коэффициент аэродинамического сопротивления для сферы дан с диапазон значений, потому что сопротивление сферы сильно зависит от Число Рейнольдса. (Поток мимо сферы или цилиндра проходит через число переходов со скоростью. На очень низкой скорости стабильно с подветренной стороны образуется пара вихрей. Как скорость возрастает, вихри становятся неустойчивыми и попеременно сбрасываются вниз по течению. При еще большем увеличении скорости пограничный слой переходы к хаотическому турбулентному течению с вихрями множества различных чешуя сбрасывается турбулентным следом от тела. Каждый из них режимы потока производят различное сопротивление на сфере.) Сравнивая плоскую пластину и призму, шар и пуля, мы видим, что форму нижнего потока можно изменить, чтобы уменьшить тащить.

---

---

Экскурсии с гидом

• Факторы, влияющие на сопротивление:
• Падающие предметы:
• Закрылки и предкрылки:
• Силы на модели ракеты:
• Разговор с модельером ракет:

---

---

Наверх

Перейти к…

Домашняя страница руководства для начинающих

---

от Тома Бенсон
Пожалуйста, присылайте предложения/исправления по адресу: benson@grc.nasa.gov

 

механик —

механик —

Содержание

Механика

Перетаскивание показаны коэффициенты C D для нескольких обтекаемых и обтекаемых форм. в зависимости от числа Рейнольдса. Сила сопротивления, F D = C D A( r U 2 /2) , зависит напрямую на это количество. Для плоской пластины перпендикулярно потоку, C Д не зависит от числа Рейнольдса в указанном диапазоне, поскольку поток отрыв происходит по острым углам пластины. Когда плита ориентирована параллельно направлению потока коэффициент сопротивления снижается более чем порядка величины и становится зависящим от числа Рейнольдса с переходом и турбулентность, вызывающая увеличение C D при более высоком Re. Это также видно, что по мере того, как тело меняет свою форму от круглого поперечного сечения до эллипса, а затем аэродинамического профиля коэффициент лобового сопротивления уменьшается. Оба круга и эллипс показывает быстрое падение C D в начале границы турбулентность слоя. До этого перехода C D не сильно зависит от числа Рейнольдса.