Кинематика кривошипно-шатунного механизма

При изучении кинематики КШМ предполагают, что коленчатый вал двигателя вращается с постоянной угловой скоростью ω, отсутствуют зазоры в сопряженных деталях, и механизм рассматривают с одной степенью свободы.

В действительности из-за неравномерности крутящего момента двигателя угловая скорость переменна. Поэтому при рассмотрении специальных вопросов динамики, в частности крутильных колебаний системы коленчатого вала, необходимо учитывать изменение угловой скорости.

Независимой переменной принимают угол поворота кривошипа коленчатого вала φ. При кинематическом анализе устанавливают законы движения звеньев КШМ, и в первую очередь поршня и шатуна.

За исходное принимают положение поршня в верхней мертвой точке (точка В₁) (рис. 1.20), а направление вращения коленчатого вала по часовой стрелке.

При этом для выявления законов движения и аналитических зависимостей устанавливают наиболее характерные точки. Для центрального механизма такими точками являются ось поршневого пальца (точка В), совершающая вместе с поршнем возвратно-поступательное движение вдоль оси цилиндра, и ось шатунной шейки кривошипа (точка А), вращающаяся вокруг оси коленчатого вала О.

Для определения зависимостей кинематики КШМ введем следующие обозначения:

l – длина шатуна;

r – радиус кривошипа;

λ – отношение радиуса кривошипа к длине шатуна.

.

Для современных автомобильных и тракторных двигателей величина λ = 0.25–0.31. Для высокооборотных двигателей с целью уменьшения сил инерции возвратно-поступательно движущихся масс применяют более длинные шатуны, чем для малооборотных.

β

 – угол между осями шатуна и цилиндра, величина которого определяется по следующей зависимости:

Наибольшие углы β для современных автомобильных и тракторных двигателей составляют 12–18°.

Перемещение (путь) поршня будет зависеть от угла поворота коленчатого вала и определяться отрезком Х (см. рис. 1.20), который равен:

.

Рис. 1.20. Схема центрального КШМ

Из треугольников А₁ АВ и ОА₁А следует, что

Учитывая, что , получаем:

Из прямоугольных треугольников А₁АВ и А₁

ОА устанавливаем, что

Откуда 

Так как

то, подставив полученные выражения в формулу для перемещения поршня, получим:

Так как  то

Полученное уравнение характеризует движение деталей КШМ в зависимости от угла поворота коленчатого вала и показывает, что путь поршня можно условно представить состоящим из двух гармонических перемещений:

где  – путь поршня первого порядка, который имел бы место при наличии шатуна бесконечной длины;

– путь поршня второго порядка, т. е. дополнительное перемещение, зависящее от конечной длины шатуна.

На рис. 1.21 даны кривые пути поршня по углу поворота коленчатого вала. Из рисунка видно, что при повороте коленчатого вала на угол, равный 90°, поршень проходит больше половины своего хода.

Рис. 1.21. Изменение пути поршня в зависимости от угла поворота коленчатого вала

Скорость поршня определяется как первая производная пути поршня по времени:

где  – угловая скорость вращения вала.

Скорость поршня можно представить в виде суммы двух слагаемых:

где  – гармонически изменяющаяся скорость поршня первого порядка, т. е. скорость, с которой двигался бы поршень при наличии шатуна бесконечно большой длины;

– гармонически изменяющаяся скорость поршня второго порядка, т. е. скорость дополнительного перемещения, возникающая вследствие наличия шатуна конечной длины.

На рис. 1.22 даны кривые скорости поршня по углу поворота коленчатого вала. Значения углов поворота коленчатого вала, где поршень достигает максимальных значений скорости, зависят от ? и ее увеличением смещаются в стороны мертвых точек.

Для практических оценок параметров двигателя используется понятие средней скорости поршня:

.

Для современных автомобильных двигателей Vср = 8–15 м/с, для тракторных – Vср = 5–9 м/с.

Ускорение поршня определяется как первая производная пути поршня по времени:

.

Рис. 1.22. Изменение скорости поршня в зависимости от угла поворота коленчатого вала

Ускорение поршня можно представить в виде суммы двух слагаемых:

где  – гармонически изменяющееся ускорение поршня первого порядка;

– гармонически изменяющееся ускорение поршня второго порядка.

На рис. 1.23 даны кривые ускорения поршня по углу поворота коленчатого вала. Анализ показывает, что максимальное значение ускорения имеет место при нахождении поршня в ВМТ. При положении поршня в НМТ величина ускорения достигает минимального (наибольшего отрицательного) противоположного по знаку значения и абсолютная величина его зависит от ?.

Рис 1.23. Изменение ускорения поршня в зависимости от угла поворота коленчатого вала

Аналитическая кинематика кривошипно-ползунного механизма

Пример решения задачи: Аналитическая кинематика кривошипно-ползунного механизма

 (содержит три этапа)

Контрольная работа по технической механике. Раздел 1. Машины и механизмы

Этап I. 

Провести аналитическое исследование кривошипно-ползунного механизма, изображенного на рис.1.1 , а именно: найти перемещение xC, скорость υС и ускорение аС ползуна С в зависимости от значения угла φ1.

Рис.1.1 Схема кривошипно-ползунного механизма

Прежде чем получить вариант с исходными данными, изучите пункт 1.4.2 Аналитический метод кинематического анализа теоретического материала и пример 1, который приводится ниже:

Пример1. Провести аналитическое исследование кривошипно-ползунного механизма, а именно: найти перемещение, скорость и ускорение ползуна С в зависимости от значения угла φ1. Для расчета принять: d =0,07м; r =0,2м; l =0,8м, ω1=1с–1, (ε1=0), φ1=π/3.

Теоретическое сопровождение задачи:

При вращении кривошипа АВ с заданной угловой скоростью ω1= d φ1/ dt

ползун С совершает возвратно поступательное движение. Такого типа механизмы используют в поршневых двигателях, насосах, компрессорах и других машинах. Для того чтобы кривошип АВ имел возможность совершать полный оборот, размеры звеньев АВ и ВС механизма должны удовлетворять неравенству

λ = AB /BC = r / l <1. (п.1)

Суть аналитического исследования кинематики данного механизма состоит в установлении геометрической (векторной) связи между положением ведущего звена (кривошипа) и положениями других (ведомых) звеньев.

В частности нас интересует связь xc=f(φ1). Зная такую связь, путем дифференцирования по времени определяется скорость υС и затем ускорение аСползуна С в зависимости от значения угла φ1. Аналогично определяется также положение, скорость и ускорение других ведомых звеньев.

Скорости ведомых звеньев. Если искомое К -е ведомое звено движется поступательно, то линейная скорость К — го звена будет определяться следующим образом

(п.2)

Координату φ1 = q называют обобщенной координатой (безразмерная величина), а

— обобщенной скоростью механизма, [ ω 1=1/ c ].

Если ведомое N -е звено совершает вращательное движение, то его угловая скорость определяется зависимостью

; (п. 3)

Здесь и –аналоги скорости для К -го поступательного и N -го вращающегося звена .

Значения и называют ещё передаточными функциями (отношениями) IK -1 и UN -1 , так как их можно преобразовать, умножив и разделив его на величину dt:

, ( п. 4)

(п.5)

Вывод: Если определить передаточные функции IK -1 и UN -1, то скорости ведомых K -го и N -го звеньев находятся как

(п.6)

Ускорения ведомых звеньев. Перепишем уравнение (п.2)

и продифференцируем его по времени. Так определим линейное ускорение aK К-го звена:

(п.7)

Величина

– аналог ускорения К-го звена, совершающего поступательное движение (вторая передаточная функция).

Угловое ускорение εN N -го звена определяется зависимостью, получаемой дифференцированием уравнения (п.3)

по dt :

(п.8)

Величина

– аналог ускорения N -го звена, совершающего вращательное движение.

В частности, если ведущее звено (кривошип) вращается равномерно, то

,

и формулы (п.7) и (п.8) упрощаются:

(п.9)

Итак, для аналитического анализа механизма необходимо найти зависимости для первых IK-1 и UN-1 и вторых I′K-1 и U′N-1 передаточных функций, а затем использовать соотношения (п.6) и (п.8) или (п.9).

___________________________________

Вычертим механизм в соответствии с данными задачи и рассмотрим замкнутый векторный контур OABCO (рис 1.2).

Рис.1.2 Замкнутый векторный контур кривошипно-ползунного механизма

Соблюдая единообразие отсчёта углов, определяющих положение звеньев, составим векторное уравнение

(п.10)

Введем угол ψ=2π –φ2 и спроектируем (п.10) на координатные оси Х и Y:

(п.11)

. (п.12)

Здесь угол ψ — (угол давления) введен для удобства, поскольку φ2 тупой угол. При этом, очевидно, что передаточная функция выражается через ψ следующим образом:

(п.13)

Решение задачи о положениях. Определим функции положения ползуна xс (φ1 ) и шатунаφ2 (φ1 ).

Из (п.14) получаем

откуда

Далее, из (п.11) получим координату положения ползуна:

. (п.14)

Расчет:

=

Решение задачи о скоростях:

Определим аналоги скорости ползуна

и шатуна

для чего продифференцируем по обобщенной координате φ1уравнение (п.12)

; (п.15)

и (п.14):

(п.16)

Сначала из уравнения (п.15) выразим аналог скорости (передаточное отношение U 2-1 ) шатуна

(п.17)

Из уравнения (п.16) с учетом (п.17) получаем аналог скорости ползуна (передаточное отношение I С-1 )

(п.18)

Выражения (п.17) и (п.18)показывают, что передаточные функции U 2-1 и I С-1 зависят только от положения механизма φ1, его геометрии и не зависят от скорости ω1 начального звена.

Угловая скорость шатуна относительно точки В :

(п.19)

Линейная скорость ползуна

(п.20)

Расчеты:

Из (п.17) и (п.19) найдем функцию, передающую вращение от кривошипа к шатуну и его угловую скорость:

Знак «–» у угловой скорости шатуна ω2 означает, что угол φ2 в последующий момент времени станет меньше, а угол ψ – больше.

Из уравнений (п.18) и (п.20) определим аналог скорости и саму скорость ползуна:

Здесь, знак «–» у линейной скорости ползуна означает, что координата x С уменьшается, ползун движется влево.

Решение задачи об ускорениях:

Поскольку ведущее звено(кривошип) вращается равномерно, то для нахождения ускорений шатуна и ползуна используем сокращенные формулы (п.9)

(п.9`)

Определим аналог ускорения шатуна

для чего продифференцируем уравнение (п.17)

по dφ1 :

Поскольку согласно (п. 17)

окончательно для U ’ 2-1 получим:

(п.21)

Аналогично найдем производную от первой передаточной функции ползуна :

Угловое ускорение шатуна вычислим по формуле

,

а линейное ускорение ползуна :

Расчет :

Ответ: В момент времени, когда выполняются условия задачи:

— положение точки С на ползуне xc =0,862 м

— угол между кривошипом и шатуном φ2= 342,30

— угол давления ψ=17,70

— угловая скорость шатуна ω2= – 0,131 1/с

— линейная скорость ползуна υ с=– 0,205 м/с

— угловое ускорение шатуна ε 2=0,222 1/с2

— ускорение ползуна ас = – 0,059 м/с2.

Приведем графики изменения рассчитанных параметров в зависимости от угла φ1, рассчитанные для двух оборотов кривошипа:

Этап II. Силовой ( динамический ) анализ механизма.

К звену ВС кривошипно-ползунного механизма (рис.1.1) приложен момент М = 12 кНм, к точке С — сила F = 20 кН. Используя результаты расчета Вашего варианта и заданные массу ползуна mc и момент инерции шатуна I2 вычислите:

1) — кинетическую энергию механизма и 2)-выполните приведение моментов и сил к звену А B. Массой кривошипа и силами трения пренебречь.

Для выполнения этапа №2 разберите пункты 1.5.3 Кинетическая энергия, приведенная масса, приведенный момент инерции механизма и 1.5.4 Приведенная сила и приведенный момент сил из теоретического материала и пример 2 после этого пункта:

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, ПРИВЕДЕННАЯ МАССА, ПРИВЕДЕННЫЙ МОМЕНТ ИНЕРЦИИ МЕХАНИЗМА

Анализ движения машинного агрегата, находящегося под действием приложенных к нему внешних сил, удобно проводить с использованием метода приведения масс и сил к какому-либо звену механизма. Он сводится к анализу динамики тела (звена приведения), к которому приведены все внешние силы и моменты. Чаще всего звеном приведения выступает ведущее звено механизма.

Кинетическая энергия механизма. Для i -го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить формулой

,

где первое слагаемое правой части – это кинетическая энергия поступательного движения центра масс звена; второе слагаемое – кинетическая энергия вращательного движения; mi – масса звена; υsi – скорость центра масс; Isi – момент инерции звена относительно центра масс; ω i – угловая скорость звена.

Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев механизма:

, (п.23)

где n – количество подвижных звеньев.

Приведенная масса механизма. Условно заменим механизм его динамической моделью. Например, кривошипно-ползунный механизм (рис. 2.1) заменим динамической моделью, состоящей из стойки и кривошипа.

Рис. 2.1 Замена кривошипно-ползунного механизма динамической моделью

Здесь ОB – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, B – точка приведения.

Уравнение (п.23) умножим и разделим на квадрат скорости точки приведения υ В :

.

Выражение в квадратных скобках имеет размерность массы (кг) и называется приведенной массой mпр механизма в точке В :

. (п.24)

Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

Тогда

, (п.25)

Приведенный момент инерции. Так как υB = ω1lAB , где lAB – длина звена приведения, ω1– его угловая скорость, то кинетическую энергию механизма можно выразить уравнением

,

где приведенный момент инерции механизма

. (п.26)

Приведенным моментом инерции механизма (используется, если звено приведения совершает плоскопараллельное движение) называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.

Важно, что величины mпр и Iпр не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.

Расчет:

υB = ω · lAB = ω · r =0,2 м/с;

Приведенная сила и приведенный момент сил. Приведенной силой FПр называется условная сила, приложенная в точке приведения, и определяемая из равенства элементарной работы этой силы (в единицу времени) А = FПр · υпр сумме работ сил Fi и пар сил Mi, действующих на звенья механизма.

(п.27)

Аналогично определяется приведенной момент сил MПр — условный момент сил, действующий на звено приведения, и определяемый из равенства элементарной работы (в единицу времени) А = M Пр · ω сумме работ сил Fi и пар сил Mi , действующих на звенья механизма.

(п.28)

Расчет:

Здесь при расчете учтены направления скоростей υС и силы F , ω2 и момента M.

Таким образом, динамической моделью механизма является механизм первого класса, для угла поворота кривошипа φ1=π/3:

— кинетическая энергия механизма Екин=0,764Дж;
— приведенная масса m пр = 38,25 кг;
— приведенные момент инерции I Пр = 1,53кг∙м2;
— приведенные сила F Пр =12,64 Н ; и
— момент сил М Пр = 2,53 кНм;

Графики изменения рассчитанных параметров в зависимости от угла φ1, рассчитанные для двух оборотов кривошипа:

Этап III.

Рассчитайте для данных задачи ход ползуна S0= Smax – Smin и максимальные значения углов давления ψ1 max и ψ2 max. Рассчитайте новое значение эксцентриситета d 1, при котором ход ползуна увеличится в 1,1 раза.

Для выполнения этапа №3 разберите параграф 2.3 ПРИМЕРЫ МЕТРИЧЕСКОГО СИНТЕЗА КРИВОШИПНО-ПОЛЗУННОГОМЕХАНИЗМА С УЧЕТОМ УГЛОВ ДАВЛЕНИЯ и пример 3:

Пример 3. Заданы : r —длина кривошипа АB, l — длина шатуна ВC, d — эксцентриситет.

Требуется определить: S0= Smax – Smin – ход ползуна, ψ1max и ψ2max — максимальные значения углов давления.

Расчетные схемы рис. 3.1 и 3.2:

Рис. 3.1 Углы давления в кривошипно-ползунном механизме

Рис. 3.2. Крайние положения ползуна (мертвые точки) в кривошипно-ползунном механизме

Расчетные уравнения (из рассмотрения схем):

(п.29 )

Для определения трех неизвестных параметров схемы составлено три уравнения. Их решение не составит труда

УКАЗАНИЯ по заполнению ответов

1. Для обозначения размерности следует использовать систему СИ.

2. Числа типа

q = 1,614•10−19 Кл,

υ = 2,28•107 м/с

следует представлять в виде:

q =1,614Е−19 Кл,

υ = 2,28Е7 м/с.

Обратите внимание на два обстоятельства.

Первое: приводим число к нормализованной записи, сохранив в ней единицы, т. е.

489,567 •10−6 = 4,89567 •10−4;

0,0067842•10−19= 6,7842•10−22.

Второе: после запятой оставляем три значащих цифры:

4,89567 •10−4= 4,896 •10−4 =4,896Е−4;

6,7842•10−22= 6,784•10−22 = 6,784Е−22.

Букву E набираем латиницей!

3. При решении задач не ищите готовых формул для нахождения ответа. Исходите из фундаментальных, основополагающих законов и постулатов и выводите расчетную формулу сами!

Рассмотрим кинематику кривошипно – шатунного механизма (КШМ-а) поршневого мотора.

Случайная страница О проекте Прислать материал Контакты

Дата добавления: 2014-11-24 | Просмотров: 1349 Тема крутящего момента Роторные двигатели Когда давление газов на первом этапе горения топлива максимально, т. к. в это время объем камеры сгорания минимален, и работа совершаемая газами тоже наиболее велика, то в это миг крутящий момент на валу мотора от работы таких газов равен нолю. Ибо поршень в этой фазе работы КШМ-а находится в верхней мертвой точке и плечо рычага кривошипа равно нолю. Вся кинематика мотора (если это одноцилиндровый двигатель) движется лишь под воздействием сил инерции массы движущихся частей поршневой и кривошипно-шатунной группы двигателя. Именно для этого на поршневые моторы и ставят маховики, чтобы усилить инерционность этой части деталей двигателя. Т.е. на этом этапе работы поршневого мотора длинные осевые линии плеча кривошипа и шатуна выстроились одну прямую линию, которая параллельна вектору силы расширяющихся газов. Поэтому вся сила этих газов в данный момент тратится на деформацию конструктивных элементов поршневой и кривошипно-шатунной группы и полезная работа газов расширения в этот миг полностью отсутствует. Далее – под действием инерции вращения вал двигателя поворачивается, и движение кривошипа приводит к постепенному увеличению плеча, которое воспринимает крутящий момент, т. е. величина полезной силы расширяющихся газов возрастает. Величина нарастания значения плеча кривошипа постепенно увеличивается до значения углового расстояния в 60 град. от положения верхней мертвой точки. (РИС.) Именно в этой позиции возможно максимально эффективная работа КШМ-а, но время получения максимально возможного крутящего усилия (крутящего момента) уже утеряно, ибо по мере углового движения вниз верхней точки плеча кривошипа, вниз движется и поршень и давление рабочих газов в камере сгорания значительно падает… То есть сила газов расширения в момент наиболее высокого КПД уже не так велика, как в верхней мертвой точке. Далее, вал двигателя с кривошипом продолжает вращение и проекция плеча кривошипа по отношению к вектору силы расширяющихся газов снова начинает уменьшаться… При этом по мере движения поршня вниз и дальнейшего увеличения объема расширения камеры сгорания, давление газов в ней падает, а значит падает и усилие давления этих газов на поршень. Следовательно, на линии расширения газов и угловом пути плеча кривошипа после достижения им положения в 60 град. от верхней мертвой точки, величина крутящего момент резко падает, так как к этому приводит сложение двух процессов — падение движущего поршень давления рабочих газов и резкое уменьшение воспринимающего силу этого давления плеча кривошипа. В нижней мертвой точке продольные оси шатуна и плеча кривошипа снова выстраиваются в одну линию, и давление рабочих газов снова бессмысленно тратит свою уже небольшую силу лишь на бессмысленную деформацию элементов мотора, а движущиеся детали мотора продолжают вращаться лишь под действием инерции своих масс. По сути дела КШМ выдает силу крутящего момента на вал двигателя лишь дробными, последовательными пульсациями — серией многочисленных, но кратковременных толчков. Все автомобилисты ощущают все прелести именно такого режима работы поршневого мотора с КШМ-ом особенно в моменты, когда надо с некоторой средней скорости, если идешь на высшей передаче и теряешь инерцию движения, вдруг резко ускориться- то есть снять с мотора мощное усилие крутящего момента. Если не переходить на низшую передачу, просто резко попытаться увеличить обороты мотора на прежней передаче и нажать на педаль «газа», то получим не мощное тяговое усилие, а лишь задыхающееся тарахтение и вибрацию мотора, готового заглохнуть… Это именно проявил себя малоэффективный режим работы КШМ-а, который не способен эффективно снять крутящий момент при невысокой частоте вращения вал. Приходится в этом случае переходить на нижнюю передачу и резко нажимать педаль газа, чтобы увеличить обороты мотора, тем самым обеспечить большое количество «силовых толчков» КШМ-а в единицу времени и увеличить тяговое усилие. А вот электромоторы, которые переводят рабочую мощь электромагнитных сил в своих обмотках в простое вращательное движение без всяких малоэффективных механизмов – посредников, не страдают такой болезнью. Именно поэтому многие автомобилисты с завистью наблюдают, как легко и мощно стартуют со светофоров громоздкие и тяжелые троллейбусы, обгоняя в стартовом импульсе легкие и вроде бы мощные легковые авто. То же можно сказать и о стартовом импульсе гибридных автомобилей, где стартовый импульс (крутящий момент на старте) обеспечивает электромотор.   Итак – КШМ – это неизбежный и тяжелый порок поршневых моторов, который резко снижает их эффективность, увеличивает их громоздкость, повышает цену и уменьшает надежность. Поэтому уже не менее ста лет идет, пока еще безуспешная работа, по созданию бесшатунных схем поршневых двигателей. Работы идут сто лет, но серьезной отдачи от нее пока не видно, так как сама схема поршневого мотора давно исчерпала свои возможности в плане принципиального совершенствования. Именно поэтому почти всю историю техники осуществляются попытки создать более эффективную и инженерно совершенную конструкцию мотора без применения поршней с возвратно – поступательным движением. Именно таким направлением является линия создания роторных машин с вращательным движением главного рабочего элемента. 1 | 2 | 3 | 4 | 5 | 6 |

Кривошипно-шатунный механизм (КШМ).

Маятник Капицы » РобоВики

Данная статья является вводной теорией к занятию по робототехнике «Кривошипно-шатунный механизм из Lego EV3″

В этой статье

1. Первые КШМ
2. КШМ в паровых машинах
3. КШМ в двигателях внутреннего сгорания
4. Маятник Капицы

Первые КШМ

Первые упоминания об использовании кривошипно-шатунного механизма можно отнести ко временам Древнего Рима (примерно III век н.э.). Машина для распиливания каменных блоков передавала вращение от водяного колеса с помощью зубчатой передачи на кривошипно-шатунный механизм, который преобразовывал вращательное движение в возвратно-поступательное движение полотна пилы. Также такие устройства могли использоваться на древних лесопилках.

Схема водяного древнеримского распиловочного станка с КШМ

Большого распространения такие машины не получили – деревянные части из-за большого количества трущихся деталей быстро изнашивались и требовали частого ремонта, а рабский труд был намного дешевле и не требовал большой квалификации рабочих.

В XVI веке кривошипно-шатунный механизм появился на деревянных самопрялках. Самопрялка – это ручной станок для прядения нити из шерсти, состоящий из двух катушек. В самопрялке для скручивания нити использовался принцип ременной передачи. Раньше большую катушку приходилось раскручивать рукой. К самопрялке добавили педаль. Нажимая ногой на педаль, работник смог раскручивать катушку без использования рук. Этот механизм упростил работу и позволил за то же время производить больше пряжи. В данном устройстве возвратно-поступательное движение педали передавалось через деревянный шатун на кривошип и преобразовывалось во вращательное движение большой катушки (шкива).

Самопрялка с педалью и КШМ позволяла освободить руки и сделать работу более производительной

КШМ в паровых машинах

Начиная с начала XVIII века большую популярность среди изобретателей и ученых начинают получать паровые машины. Первый паровой двигатель для водяного насоса построил в 1705 году английский изобретатель Томас Ньюкомен для выкачивания воды из глубоких шахт.

Позднее устройство парового двигателя было усовершенствовано шотландским инженером и механиком Джеймсом Уаттом (1736-1819). Кстати, именно Джеймс Уатт ввел в оборот термин «лошадиная сила», а его именем назвали единицу мощности Ватт. Паровая машина Уатта получила сложную систему связанных тяг, а планетарная зубчатая передача преобразовывала возвратно-поступательное движение поршня во вращательное движение маховика (большого тяжелого колеса). Данная паровая машина стала универсальной, так как в отличие от машины Ньюкомена поршень имел рабочий ход в обе стороны. Машина Уатта получила широкое распространение на ткацких фабриках, в металлургии, при строительстве первых паровозов для железных дорог XVIII века.

Паровая машина Джеймса Уатта. Вместо кривошипа — сложная планетарная зубчатая передачаШотландский изобретатель Джеймс Уатт (James Watt)

Нужно сказать, что паровыми машинами занимались в те времена очень многие изобретатели. Так, в Российской Империи свою двухцилиндровую паровую машину изобрел инженер Иван Иванович Ползунов (1728-1766).

В XIX веке паровую машину Уатта упростили, заменив сложный планетарный механизм на кривошипно-шатунный механизм.

Паровая машина с кривошипно-шатунным механизмомСхема паровой машины с кривошипно-шатунным механизмом

Паровая машина с КШМ нашла широкое применение при строительстве первых автомобилей на паровой тяге и паровозов, перевозящих грузы по железной дороге.

Паровоз

КШМ в двигателях внутреннего сгорания

До этого мы рассматривали использование кривошипно-шатунного механизма в паровых двигателях. В паровом двигателе топливо сгорает в печи (вне цилиндра) и нагревает водяной котел, и уже водяной пар в цилиндре толкает поршень.

В двигателе внутреннего сгорания топливная смесь (воздух + газ, или воздух + бензин и т.д.) поджигается внутри цилиндра и продукты горения толкают поршень. Сокращенно такие двигатели называют ДВС.

Первый одноцилиндровый ДВС на газовом топливе построил в 1860 году в Париже французский изобретатель Жан Ленуар.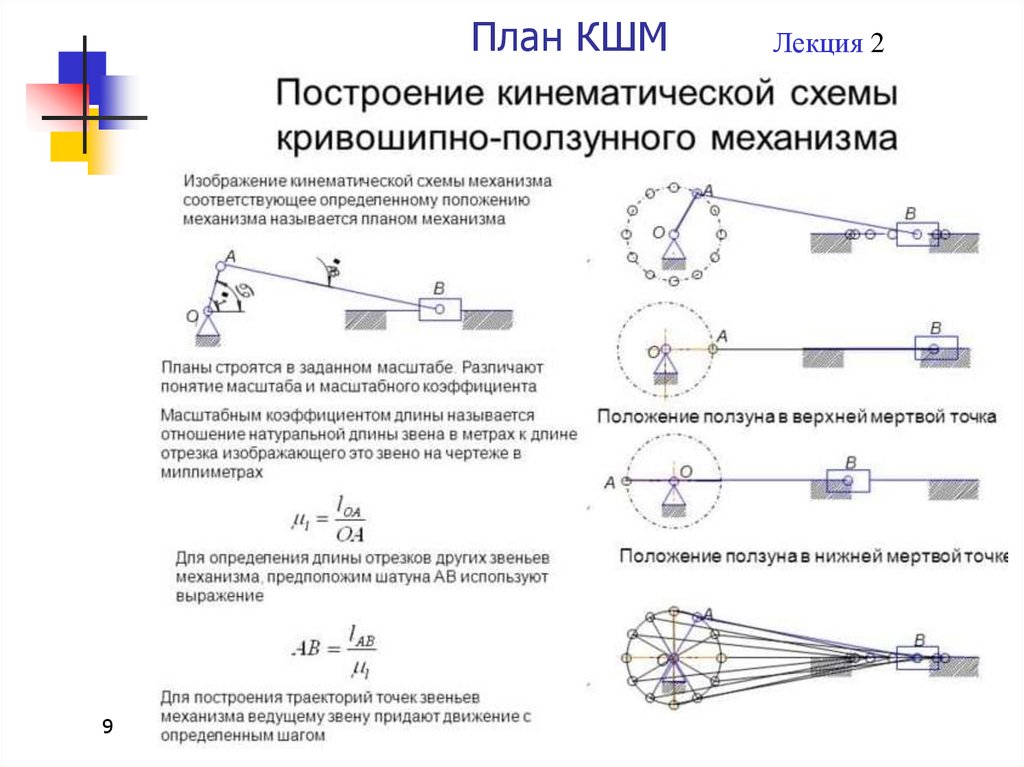

Двигатель внутреннего сгорания Жана Ленуара (внешне очень похож на паровую машину)

Однако широкое применение двигатели внутреннего сгорания нашли в конце XIX века после получения керосина и бензина из нефти. Появление жидкого топлива позволило создать экономичные двигатели небольшой массы, которые можно было использовать для привода транспортных машин.

В 1881-1885 гг. российский изобретатель Огнеслав Костович сконструировал и построил в России восьмицилиндровый двигатель мощностью 59 кВт.

Двигатель внутреннего сгорания Огнеслава Костовича

В 1897 г. немецким инженером Рудольфом Дизелем был спроектирован и построен первый двигатель с воспламенением от сжатия. Это был компрессорный двигатель, работающий на керосине, впрыскиваемом в цилиндр при помощи сжатого воздуха.

Рудольф Дизель и его двигатель внутреннего сгорания

Все эти ДВС имели схожие черты и использовали кривошипно-шатунный механизм для преобразования возвратно-поступательного движения поршня во вращательное движение коленвала.

Давайте посмотрим на схему устройства современного двигателя внутреннего сгорания.

Схема кривошипно-шатунного механизма в двигателе внутреннего сгорания

Общие определения:

Поршень совершает возвратно-поступательное движение вдоль цилиндра – он ходит вверх и вниз.

Шатун – деталь, связывающая кривошип и поршень.

Кривошип – условная деталь, которая связывает шатун с коленвалом.

Противовес снижает вибрации при вращении коленвала.  

Блок цилиндров – корпус, в котором находятся цилиндры двигателя.

Поршневой палец – цилиндрическая деталь, ось вращения шатуна относительно поршня.

Коленвал (коленчатый вал) – ось вращения ступенчатой формы.

Верхняя мертвая точка – крайнее верхнее положение поршня, где меняется направление его движения.

Нижняя мертвая точка — крайнее нижнее положение поршня, где меняется направление его движения.

Ход поршня — расстояние между крайними положениями поршня. Равно удвоенному радиусу кривошипа.

Блок цилиндров, поршень с шатуном и коленвал

Видео:

1. Старинная русская прялка с кривошипно-шатунным механизмом 
2. Паровая машина. Джеймс Уатт 
3. Принцип работы противовесов

Литература:

1. КИНЕМАТИКА И ДИНАМИКА КРИВОШИПНОШАТУННОГО МЕХАНИЗМА ПОРШНЕВЫХ ДВИГАТЕЛЕЙ 

Обычный маятник, если перевернуть его кверху ногами, неустойчив. Для него крайне трудно найти верхнюю точку равновесия. Но если совершать быстрые вертикальные возвратно-поступательные колебания, то положение такого маятника становится устойчивым.

Петр Леонидович Капица

Советский академик и нобелевский лауреат по физике Петр Леонидович Капица (1894 — 1984) использовал модель маятника с вибрирующим подвесом для построения новой теории, которая описывала эффекты стабилизации тел или частиц. Работа Капицы по стабилизации маятника была опубликована в 1951 году, а сама модель получила название «маятник Капицы». Более того, было открыто новое направление в физике — вибрационная механика. Данная модель позволила наглядно показать возможности высокочастотной электромагнитной стабилизации пучка заряженных частиц в ускорителях.

Владимир Игоревич Арнольд

Другой советский математик и академик Владимир Игоревич Арнольд (1937-2010), который был заместителем Капицы, вспоминал его слова:

«Он (Капица — примечание) сказал: «Вот смотрите — когда придумывается какая-то физическая теория, то прежде всего надо сделать маленький какой-нибудь прибор, на котором его наглядно можно было-бы продемонстрировать кому угодно. Например, Будкер и Векслер хотят делать ускорители на очень сложной системе. Но я посмотрел, что уравнения, которые говорят об устойчивости этого пучка, означают, что если маятник перевернут кверху ногами, он обычно неустойчив, падает. Но если точка подвеса совершает быстрые вертикальные колебания, то он становится устойчивым. В то время как ускоритель стоит много миллионов, а этот маятник можно очень легко сделать. Я его сделал на базе швейной электрической машинки, он вот здесь стоит». Он нас отвел в соседнюю комнату и показал этот стоящий  вертикально маятник на базе швейной машинки».

Демонстрация динамической стабилизации перевернутого маятника с помощью электробритвы

У математика Арнольда не было своей швейной машинки, и он огорчился. Но у него была электробритва «Нева», из которой и был собран перевернутый маятник. К сожалению, в первой конструкции маятник падал. Тогда Арнольд вывел формулу и увидел, что длина маятника не должна быть больше 12 сантиметров. Известный математик укоротил подвес до 11 сантиметров и все получилось.

Давайте посмотрим, какие силы действуют на «маятник Капицы». После прохождения верхней мертвой точки подвес маятника начинает тянуть грузик вниз. После прохождения нижней мертвой точки подвес толкает грузик вверх. Так как углы вежду векторами сил в верхней и нижней точке разные, то сумма их векторов дает силу, направленную к оси вертикальных колебаний маятника. Если эта сила больше силы тяжести, то верхнее положение маятника становится устойчивым.

А эта формула описывает взаимосвязь частоты вибраций подвеса, амплитуды колебаний и длины жесткого подвеса.

Видео:

1. GetAClass. Маятник Капицы 
2. Маятник Капицы: диалог академика Арнольда и Капицы, вывод формулы

Кинематика кривошипно-шатунного механизма — классический анализ

Это первое из серии руководств в категории Механика машин исследует ползунок и рукоятка механизмы .

Первые три урока исследуют кинематику ползунково-кривошипного механизма, т. е. перемещение, скорость и ускорение элементов без привязки к силам или моментам, после чего три учебники изучить кинетика в том числе диаграммы свободных тел сил, сил инерции, крутящего момента коленчатого вала и усилий и балансировки.

Традиционные исследования в области машиностроения предпочитают масштабирование графические методы анализа, например диаграмма Клейна для кривошипные механизмы. Это отражало практику проектирования до появления компьютеров. были доступны. Недостатком графических методов является то, что основные принципы не всегда ясны. Кроме того, масштабная схема относится только к одному положению механизма и необходимо повторить для каждой требуемой позиции. Компьютеры произвели революцию в проектировании и анализе механизмов. выполнять сложные и длительные расчеты для всего диапазона входных данных параметры.

Есть несколько способов получить кинематические характеристики механизм. Первый подход (предмет этого урока) выводит выражение для смещения ползунка от геометрия, а затем выводит выражения для скорости и ускорения ползуна последовательным дифференцированием перемещения.

Второй подход использует диаграммы скорости и ускорения строится по известным параметрам. Неизвестные скорости и затем рассчитываются ускорения исходя из геометрии диаграмм. второй учебник объясняет этот метод.

В третьем уроке неизвестно скорости и ускорения получаются из векторные уравнения .

Для этих учебных пособий я предполагаю, что читатель имеет разумное понимание кинематика движения самолета. В этом уроке я представил исчисление в пошаговых деталях, поскольку я знаю, что это часто является областью трудность.

На приведенной ниже схеме показаны основные части ползункового и кривошипного механизма. Ползун, например, может быть поршнем в цилиндре или линейным приводной элемент в машине. Таким образом, первичный ввод либо крутящий момент, приложенный к шатуну, либо сила, приложенная к слайдеру.

Для анализа мы используем параметры, определенные на диаграмме ниже.

• Шатун ab имеет длину R и вращается против часовой стрелки с постоянной угловой скоростью ω относительно центра вращения в точке а. Его положение определяется углом поворота кривошипа θ.
• Шатун bc имеет длину L
• Точка соединения штифта ползуна c ограничена в перемещении вдоль его горизонтальной оси х. x = 0, когда угол поворота коленчатого вала θ = 0
• φ угол между шатуном и осью x
• Линия бд — проекция точки b на прямую ac , перпендикулярную ось х.

Наши задачи:

1. Получить выражение для x (горизонтальное перемещение ползуна c в зависимости от угла θ (угла кривошипа).
2. Дифференцируйте выражение от 1 по времени, чтобы получить выражение для скорости точки ползуна с
3. Продифференцируйте выражение от 2 по времени, чтобы получить выражение для ускорения точки ползуна c.

Получите выражение для x

Во-первых, обратите внимание, что расстояние по горизонтали от точки до в начало координат при x = 0 равно (R + L).

Таким образом, для любых углов θ и φ    x = (R + L) — (ad + d c ) = (R + L} — (R.cos θ + L.cos φ) …………….. (i)

Мы должны преобразовать член (cos φ) в выражение в θ.

(Примерно, учебники часто замените выражение, полученное из степенного ряда, вместо cos(φ), что упрощает последующие дифференциации. Тем не менее это хороший обновление для дифференциального исчисления, чтобы продолжить с оригинала выражение.)

Это выражение, которое мы решили найти для горизонтальное смещение x ползунка c в зависимости от θ.

Используется в качестве чека для вычислить два значения x, когда плечо кривошипа R выровнено с шатун L, обозначаемый в горизонтальном кривошипном механизме* как внутренняя мертвая точка (idc) и наружная мертвая точка (odc), соответствующая углам поворота коленчатого вала θ = 0° и 180° соответственно. (odc – idc)   – это 90 004 штриха 90 005. механизма.

* При вертикальном расположении кривошипа соответствующие термины — верхняя мертвая точка (ВМТ) и нижняя мертвая точка. (БДК). Эти термины также используются для внутреннего поршневого привода. двигатели внутреннего сгорания для всех ориентаций цилиндров.

Следовательно, ход = 2R, что соответствует геометрии механизма.

График ниже показывает смещение x против угла кривошипа за один полный оборот кривошипа вычислено из приведенного выше выражения с n = 3 и R = 1m, L = 3m.. На втором графике для x = (1 — Cosθ) сравниваются полученные выражение синусоидальной формы. Переписка с синусоидальная форма увеличивается по мере увеличения отношения n.

Обратите внимание на неотъемлемую характеристику кривошипа механизма, что между θ = 0° и θ = 90° на ход вперед и между θ = 270° и θ = 360° при обратном ходе ползунок перемещается значительно больше, чем 50% длины хода.

Получите выражение для скорости v ползуна

c .

В этом выражении x является функцией переменной θ (кривошип угол). Для скорости v ползуна c требуется производная по времени dx/dt, для которой мы используем цепное правило:

R и (в данном случае) ω являются константами, поэтому дифференцирование становится:

Взяв производную по θ от каждого члена в brackets:

d/dθ of constants 1 and n = 0

d/dθ of (- cosθ) = (+ sin θ)

График ниже показывает зависимость скорости v от угла поворота коленчатого вала θ для одного полный оборот кривошипа, вычисляемый по выражению выше для отношения n = 3, с R = 1m, L = 3m и ω = 2π радиан/сек (60 об/мин).

Обратите внимание, что максимальные абсолютные скорости ползунка достигаются при угол поворота коленчатого вала θ < 90° при ходе наружу и при θ > 270° на обратном ходе, а не на среднем вращении положение кривошипа.

Получить выражение для линейного ускорения a ползуна

c

Получить выражение для линейного ускорения a ползуна c в зависимости от угла поворота коленчатого вала θ дифференцируем выражение для скорости v относительно времени, снова используя цепное правило:

ползуна против угла кривошипа за один полный оборот плечо кривошипа, рассчитанное с использованием полученного выше выражения для отношения n = 3, при R = 1 м, L = 3 м и ω = 2π радиан/сек (60 об/мин).

Обратите внимание, что ускорение ползунка значительно выше при внутренней мертвой точки в конце хода, чем в наружной мертвой точке центральный конец.

Переходы между положительными и отрицательными ускорениями значительным в контексте сил инерции (см. будущее руководство)

 Двойные отрицательные пики по обе стороны от внешнего мертвого центральное положение возникает в результате комбинированного действия двух отдельных компоненты ускорения, известные как первичные и вторичное ускорение , соответствующее двум терминам внутри скобки предыдущего выражения. Эти компоненты важны при рассмотрении балансировки инерции силы (см. будущий учебник).

Ждем ваших отзывов по адресу:

[email protected] 

Анализ кинематики двойного кривошипно-ползункового механизма на основе Simulink

Заголовки статей

Оптимизация конструкции основания и обода турбинной лопатки в форме двойной буквы T с помощью трехмерного метода конечных элементов
стр. 239

Исследование верифицируемой расчетной модели конструктивного дефекта механической сборки
стр. 244

Численное исследование влияния формы передней части на поле внешнего обтекания большегрузного автомобиля при боковом ветре
стр. 249

Анализ и оптимизация конструкции манипулятора для сгребания угля на базе ANSYS
стр. 254

Кинематический анализ двойного кривошипно-ползункового механизма на основе Simulink
стр. 258

Исследование конструкции храповой муфты в Winder
стр. 263

Оценка сходства модели сборки на основе сопоставления реляционного графа с атрибутами компонентов
стр. 270

Оптимизация дизайна и численное моделирование аэродинамической формы самолета
стр. 275

Инновационный дизайн метода формования и машины для несферических сладких клецок
стр. 279

Главная Прикладная механика и материалы Прикладная механика и материалы Vols. 215-216 Анализ кинематики двойного кривошипно-ползункового механизма…

Предварительный просмотр статьи

Аннотация:

Моделирование и анализ кинематической модели двойного кривошипно-ползункового механизма с помощью инструментов Simulink платформ MATLAB. Механизм представляет собой систему, в которой ее кинематические уравнения могут построить имитационную модель, а ее начальное положение может таким образом определять соответствующие параметры модели. можно получить результаты моделирования кинематических параметров. Наконец, возьмите основной передаточный механизм платформенной печатной машины в качестве примера, чтобы проверить точность и эффективность предлагаемого метода.

Доступ через ваше учреждение

использованная литература

[1] Су Хэпин, Пэн Дань, Линь Цзишунь. Анализ характеристик движения отклоняющего ползунково-кривошипного механизма [J]. Журнал механических трансмиссий, 2011 (09): 45-48.

[2] Цзи Сяохун. Анализ ограниченного позиционного угла и коэффициента отношения скорости движения для плоского механизма нижней пары [J]. Механические исследования и применение, 2011 (01): 17-18.

[3] Чи Литинг. Анализ характеристик быстрого возврата в плоском четырехзвенном рычажном механизме[J]. Машиностроение и автоматизация, 2011(04): 161-162, 165.

[4] Цзян Иньцзян, Мо Цзиньцю. Оптимальный синтез регулируемых кривошипно-ползунковых соединений для ультразвукового контроля швартовной цепи [J]. Машиностроение и автоматизация, 2011(04): 19-22.

[5] Хэ Венде, Ван Чун, Чжан Ли, Лай Лили. Методы проектирования кривошипно-ползункового механизма на основе Matlab[J]. Журнал Ланьчжоуского политехнического колледжа, 2011 (04): 57–59.

[6] Цзо Вэйвэй, Дэн Юаньчао, Вэй Бин. Кинематический анализ и динамическое моделирование механизма плоского звена на основе MATLAB[J]. Журнал Технологического университета Хубэй, 2011 (04): 86-88.

Цитируется

[PDF] Кинематика и кинетический анализ механизма с ползунком в линейном четырех цилиндрах Samand Engine

• DOI: 10.1115/1.859933.Paper10
• CORPUS ID: 110222774

3333330 @ARTICLIC @ARTICALI @ARTICALI @ARTICALI @ARTICLIC @ARTICLIC @ARTICLIC @ARTICLIC @ARTICLIC @ARTICLICS @ARTICLICS @ARTICLICS. title={Кинематика и кинетический анализ кривошипно-ползункового механизма в четырехцилиндровом линейном двигателе Отто}, автор = {Масуд Солтани Мохаммади и Мохаммад Реза Асади и Мохаммад Ранджбаркохан и Махди Мохаррампур}, journal={Исследования в области машиностроения}, год = {2011}, объем = {3}, страницы = {85-95} }

• М. Мохаммади, М. Асади, Махди Мохаррампур
• Опубликовано 31 марта 2011 г.
• Машиностроение
• Исследования в области машиностроения

Nissan Z24 является одним из многочисленных автомобилей в Иране. Отчеты MegaMotor показывают высокий уровень повреждений коленчатого вала и шатуна этого двигателя автомобиля. Необходимо провести полное исследование кривошипно-кривошипного механизма из-за дороговизны ремонта и замены этих деталей и их обратного воздействия на другие детали, такие как блок цилиндров и поршень. Результаты первоначальных исследований показывают, что важной причиной выхода из строя этих деталей является использование пониженной передачи в… 

Просмотр через издателя

Academicjournals.org

Параметрическое исследование геометрических и кинетических аспектов ползунково-кривошипного механизма

• Иман Пишвайе Наини, А. Кешаварзи, Иман Фаттахи
9001 Engineering Journal and Iran Journal 900 Технология, операции машиностроения
• 2018

Надлежащая работа кривошипно-кривошипных механизмов режущих машин зависит от правильного подбора их параметров. Силы реакции в суставах и внутренний крутящий момент изменяются при…

Расчетное управление крутящим моментом на основе генетического алгоритма кривошипно-ползункового механизма гребного винта корабля механизм в гребном винте корабля были сделаны и продолжают исследоваться. В данной статье представлено управление положением…

Интеллектуальное управление положением кривошипно-кривошипного механизма в корабельном гребном винте

Проведено компьютерное моделирование, доказано достижение асимптотической устойчивости и результаты подтверждают высокую отслеживаемость и эффективность предложенной схемы управления.

Отслеживание позиции механизма ползунков с использованием контроллера PID, оптимизированного методом Зиглера Никола

• F. Ahmad, Ahmad Lukman Hitam, K. Hudha, H. Jamaluddin

• Инженерные председатели

• 2011

. на реакцию отслеживания положения кривошипно-шатунного механизма с пропорционально-интегрально-дифференциальным управлением (ПИД), управляемого двухфазным шаговым двигателем. В этом…

Динамический анализ и управление маятником, приводимым в движение двигателем постоянного тока через кривошипно-кривошипный механизм Физика

Механические системы и обработка сигналов

2022

Влияние самосмазывающегося покрытия и движения на снижение трения и износа мягкой стали и анализ данных с помощью машинного обучения

• Nayem Hossain, M. Chowdhury, F. Djavanroodi

• Материаловедение

  Материаловедение

• 2021

Концепция машинного обучения (ML) включена в это исследование для спонтанного определения закономерностей наборов данных и создания моделей прогнозов. для прогнозирования данных, выходящих за пределы экспериментального диапазона.

Характеристики трения и износа керамического композита при разнонаправленных движениях

• M. Chowdhury, B.A. Shuvho, Nayem Hossain, Mahamudul Hassan, U.K. Debnath, Shahin Mia

• Материаловедение

  Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology

• 2021

Характеристики трения и износа нержавеющей стали, диффузионно обработанной керамикой на основе кремния, были исследованы с помощью игольчатого метода. конфигурация диска при возвратно-поступательном движении, вращательном движении и…

Анализ поверхностных покрытий и их влияние на снижение трибологических свойств алюминия с покрытием при движении с помощью метода машинного обучения

• M. Chowdhury, Nayem Hossain, Mr Rajib Nandee

• Материаловедение

• 2021

Популярность алюминия с покрытием привлекает значительное внимание во многих отраслях промышленности благодаря его удельной прочности, коррозионной стойкости и коррозионной стойкости. возможность вторичной переработки. Однако из-за…

Модельный подход к проектированию коленчатого вала для производства порошковых металлов

• V. Angelopoulos

• Материаловедение

• 2015

Коленчатый вал — это компонент, который используется для преобразования возвратно-поступательного движения во вращательное или наоборот. За прошедшие годы классические технологии производства не оставили места для новых приложений…

Подход к методу выделения признаков воздействия на основе улучшенного модального разложения и анализа сингулярных значений

• Fengfeng Bie, K. Horoshenkov, Jin Qian, J. Пей

• Инженерия, информатика

  Journal of Vibration and Control

• 2018

Предложены усовершенствованные методы обработки сигналов разложения по вариационным модам и разложения по сингулярным числам для выделения нестационарных характеристик удара применительно к мониторингу состояния поршневого механизма.

ПОКАЗАНЫ 1-7 ИЗ 7 ССЫЛОК

Динамическое моделирование и идентификация ползунково-кривошипного механизма

• J. Ha, R. Fung, Kun-Yung Chen, S. Hsien

• Engineering

• 2006

Производительность и динамический анализ робота на основе глазкости. Цветичанин Р. Маретич

Машиностроение

2000

Инженерная механика

• B. C.

• Машиностроение

  Природа

• 1932

Книга написана с точки зрения студента-инженера, и применение принципов механики рассматривается в соответствии с инженерной практикой. Таким образом, примеры…

Угол передачи в механизмах (Треугольник в мех.)

• Шринивас С. Балли, С. Чанд

• Машиностроение

• 2002

9094 8-е издание 1-я механика,0049

Нью-Йорк, Джон Уилли,

1998

Динамический анализ режущего механизма

• Мех. Мах. Теория,

• 2000

Кривошипно-ползунковая связь — 3D-анимация

Эта статья нуждается в дополнительных ссылках для проверки . Пожалуйста, помогите улучшить эту статью, добавив ссылки на надежные источники. Неисходный материал может быть оспорен и удален. Найти Источники: «Связанная сжигалка»-Новости · Газеты · Книги · Scholar · JSTOR (март 2018). )

Кривошипно-ползунковая связь представляет собой четырехзвенный механизм с тремя вращающимися шарнирами и одним призматическим или скользящим шарниром. ^[1] Вращение кривошипа вызывает линейное движение ползуна, или расширение газов против скользящего поршня в цилиндре может привести к вращению кривошипа.

Кривошипные рукоятки бывают двух типов: линейные и со смещением.

1. Линейный: ползун линейного кривошипа с ползунком расположен так, что линия хода шарнирного соединения ползуна проходит через базовое соединение кривошипа. Это создает симметричное движение ползуна вперед и назад при вращении кривошипа.
2. Смещение: если линия перемещения шарнирного соединения ползуна не проходит через базовый шарнир кривошипа, движение ползуна несимметрично. Он движется быстрее в одном направлении, чем в другом. это называется быстровозвратный механизм.

Также существует два метода проектирования каждого типа: графический и аналитический.

Содержимое

• 1 Кинематика линейного кривошипа
  • 1.1 Дизайн
  • 1.2 Графический подход
  • 1. 3 Аналитический подход
• 2 Кривошипно-ползунковая конструкция со смещением
  • 2.1 Аналитический подход
• 3 инверсии ползун-кривошип
• 4 Галерея
• 5 См. также
• 7 Внешние ссылки

Кинематика рядного ползуна-кривошипа

Смещение конца шатуна примерно пропорционально косинусу угла поворота кривошипа при измерении от верхней мертвой точки (ВМТ). Таким образом, возвратно-поступательное движение, создаваемое постоянно вращающимся кривошипом и шатуном, приблизительно представляет собой простое гармоническое движение:

Икс = rcos⁡α + l {\ displaystyle x = r \ cos \ alpha + l}

где х — расстояние конца шатуна от оси кривошипа, l — длина шатуна, r — длина кривошипа, α — угол коленчатого вала измеряется от верхней мертвой точки (ВМТ). Технически возвратно-поступательное движение шатуна отличается от синусоидального движения из-за изменения угла шатуна во время цикла, правильное движение, заданное уравнениями движения поршня: 9{2}\alpha }}}

Пока шатун намного длиннее кривошипа, l>>r{\displaystyle l>>r} разница незначительна. Эта разница становится значительной в высокоскоростных двигателях, которым могут потребоваться уравновешивающие валы для уменьшения вибрации из-за этого «вторичного дисбаланса».

Механическое преимущество кривошипа, соотношение между силой, действующей на шатун, и крутящим моментом на валу, меняется на протяжении цикла кривошипа. Соотношение между ними примерно такое:

τ = Frsin⁡ (α + β) {\ displaystyle \ tau = Fr \ sin (\ alpha + \ beta) \,}

, где τ {\ displaystyle \ tau \,} — крутящий момент, а F — усилие на шатуне. Но в действительности крутящий момент максимален при угле поворота коленчатого вала менее α = 90° от ВМТ для данного усилия на поршне. Один из способов рассчитать этот угол — выяснить, когда скорость вращения малого конца шатуна (поршня) становится максимальной в направлении вниз при постоянной скорости вращения кривошипа. Скорость поршня x’ выражается как: 9{2}\alpha }}}){\frac {d\alpha}}{dt}}}

Например, для длины штока 6 дюймов и радиуса кривошипа 2 дюйма численное решение приведенного выше уравнения позволяет найти минимум скорости (максимум скорость вниз) должна быть при угле поворота коленчатого вала 73,17615° после ВМТ. Затем, используя закон синусов треугольника, обнаруживается, что угол между кривошипом и шатуном составляет 88,21738 °, а угол шатуна составляет 18,60647 ° от вертикали (см. Уравнения движения поршня # Пример).

Когда кривошип приводится в движение шатуном, проблема возникает, когда кривошип находится в верхней мертвой точке (0°) или нижней мертвой точке (180°). В эти моменты цикла кривошипа сила, действующая на шатун, не вызывает крутящего момента на кривошипе. Следовательно, если кривошип неподвижен и находится в одной из этих двух точек, он не может быть приведен в движение шатуном. По этой причине в паровозах, колеса которых приводятся в движение кривошипами, шатуны крепятся к колесам в точках, отстоящих друг от друга на некоторый угол, так что независимо от положения колес при запуске двигателя хотя бы один шатун будет быть в состоянии приложить крутящий момент, чтобы начать поезд.

Конструкция

Ползунок линейного кривошипа ориентирован таким образом, что точка поворота кривошипа совпадает с осью линейного перемещения. Следящий рычаг, который является звеном, соединяющим кривошип с ползунком, соединяется со штифтом в центре скользящего объекта. Этот штифт считается находящимся на оси линейного перемещения. Следовательно, чтобы считаться ползунком кривошипа , расположенным на линии , точка поворота кривошипа должна быть на линии с этой точкой штифта. Ход((ΔR ₄ ) _max ) линейного кривошипного ползуна определяется как максимальное линейное расстояние, которое ползун может пройти между двумя крайними точками своего движения. В линейном ползунке кривошипа движение кривошипа и ведомых звеньев симметрично относительно оси скольжения. Это означает, что угол поворота коленчатого вала, необходимый для выполнения прямого хода, эквивалентен углу, необходимому для выполнения обратного хода. По этой причине линейный кривошипно-ползунковый механизм обеспечивает сбалансированное движение. Это уравновешенное движение подразумевает и другие идеи. Если предположить, что кривошип приводится в движение с постоянной скоростью, время, необходимое для выполнения прямого хода, равно времени, необходимому для выполнения обратного хода.

Графический подход

Графический метод проектирования встроенного ползунково-кривошипного механизма включает использование нарисованных от руки или компьютерных схем. Эти диаграммы нарисованы в масштабе для облегчения оценки и успешного проектирования. Базовая тригонометрия, практика анализа взаимосвязи между элементами треугольника для определения любых неизвестных значений, может использоваться с графическим компасом и транспортиром вместе с этими диаграммами для определения требуемой длины штриха или звена.

Когда необходимо рассчитать ход механизма, сначала определите уровень земли для указанного ползунково-кривошипного механизма. Этот уровень земли является осью, на которой расположены как точка поворота кривошипа, так и скользящий штифт. Нарисуйте точку поворота шатуна в любом месте на этом уровне земли. Как только штифты будут установлены правильно, установите графический компас на заданную длину звена шатуна. Поместив точку компаса в точку поворота кривошипа, поверните компас, чтобы получился круг с радиусом, равным длине кривошипа. Этот вновь нарисованный круг представляет потенциальное движение кривошипа. Далее нарисуйте две модели механизма. Эти модели будут ориентированы таким образом, чтобы отображались оба крайних положения ползунка. После того, как обе диаграммы будут нарисованы, линейное расстояние между втянутым ползунком и выдвинутым ползунком можно легко измерить, чтобы определить ход ползуна-кривошипа.

Убранное положение ползуна определяется дальнейшим графическим анализом. Теперь, когда траектория кривошипа найдена, нарисуйте рычаг ползунка кривошипа в положении, которое помещает его как можно дальше от ползунка. После рисования рукоятка должна совпадать с осью уровня земли, которая была первоначально нарисована. Затем из свободной точки на плече кривошипа нарисуйте ведомое звено, используя его измеренную или заданную длину. Нарисуйте эту длину, совпадающую с осью уровня земли, но в направлении к ползунку. Свободный конец толкателя теперь будет находиться в полностью втянутом положении ползуна. Затем необходимо определить расширенное положение ползунка. Из точки поворота кривошипа нарисуйте новый кривошип, совпадающий с осью уровня земли, но в положении, ближайшем к ползунку. В этом положении новый шатун должен располагаться под углом 180 градусов к убранному шатуну. Затем нарисуйте ссылку последователя с заданной длиной так же, как упоминалось ранее. Незакрепленная точка нового толкателя теперь будет находиться в полностью выдвинутом положении ползунка.

Теперь должно быть известно как втянутое, так и выдвинутое положение ползунка. Используя измерительную линейку, измерьте расстояние между этими двумя точками. Это расстояние будет ходом механизма, (ΔR ₄ ) _max .

Аналитический подход

Для аналитического проектирования линейного кривошипа ползуна и достижения желаемого хода необходимо определить соответствующие длины двух звеньев, кривошипа и толкателя. В этом случае кривошип будет обозначаться как 9.0587 L ₂ , а ссылка для подписчиков будет называться L ₃ . У всех линейных кривошипно-ползунковых механизмов ход в два раза превышает длину кривошипа. Следовательно, по ходу можно определить длину плеча кривошипа. Эта связь представлена ​​как:

L ₂ = (ΔR ₄ ) макс.0588) можно определить. Однако, поскольку ход механизма зависит только от длины плеча кривошипа, длина толкателя несколько незначительна. Как правило, длина ведомого звена должна как минимум в 3 раза превышать длину плеча кривошипа. Это связано с часто нежелательным повышенным ускорением или мощностью соединительного плеча.

Конструкция кривошипно-ползункового механизма со смещением

Аналитический подход

Аналитический метод проектирования кривошипно-ползункового механизма со смещением представляет собой процесс, посредством которого оценивается треугольная геометрия для определения обобщенных взаимосвязей между определенными длинами, расстояниями и углами. Эти обобщенные отношения отображаются в виде 3 уравнений и могут использоваться для определения неизвестных значений практически для любого смещения ползунка-кривошипа. Эти уравнения выражают длины звеньев, L ₁ , L ₂ и L ₃ , как функция хода, (ΔR ₄ ) _max , угол дисбаланса 8 и β 8 произвольная линия M , θ _M . Произвольная линия M — это уникальная для дизайнера линия, которая проходит через точку поворота кривошипа и крайнее убранное положение ползуна. 3 уравнения выглядят следующим образом:

Д ₁ = (ΔR ₄ ) _макс × [ (sin(θ _M )sin(θ _M — β)) / sin(β) ]

L ₂ = (ΔR ₄ ) _max × [ (sin(θ _M ) — sin(θ _M — β)) / 2sin(β) ]

L ₃ = (ΔR ₄ ) _max × [ (sin(θ _M ) + sin(θ _M — β)) / 2sin(β)8 ]

, можно рассчитать 3 длины звеньев и определить любые связанные неизвестные значения.

Инверсия ползун-кривошип

Инверсия цепи ползун-кривошип возникает, когда шатун или муфта кулисно-кривошипной связи становится заземляющим звеном, поэтому ползунок соединяется непосредственно с кривошипом. Этот перевернутый ползун-кривошип представляет собой форму ползунково-кривошипного соединения, которое часто используется для приведения в действие шарнирного соединения в строительном оборудовании, таком как кран или экскаватор, а также для открытия и закрытия распашных ворот или дверей. ^{[2] [3] [4]}

Кривошипно-ползунковый механизм представляет собой четырехзвенниковую связь, в которой кривошип вращается вместе с ползунком, который движется по прямой линии. Этот механизм состоит из трех важных частей: кривошипа, представляющего собой вращающийся диск, ползуна, который скользит внутри трубки, и шатуна, который соединяет части вместе. Когда ползунок перемещается вправо, шатун толкает колесо на первые 180 градусов поворота колеса. Когда ползунок начинает двигаться обратно в трубу, шатун тянет колесо, чтобы завершить вращение.

Различный механизм с фиксацией другого звена кривошипной цепи ползунка:

Первая инверсия

Эта инверсия получается, когда звено 1 (заземление) зафиксировано. Применение — поршневой двигатель, поршневой компрессор и т.д…

Вторая инверсия

Эта инверсия получается, когда звено 2 (кривошип) зафиксировано. Применение: механизм быстрого возврата Уитворта, роторный двигатель и т. д.

Третья инверсия

Эта инверсия получается, когда звено 3 (шатун) зафиксировано. Применение: кривошипно-шатунный механизм, колебательный двигатель и т. д.,

Четвертая инверсия

Эта инверсия получается, когда звено 4 (ползунок) зафиксировано. Применение: ручной насос, маятниковый насос или двигатель Bull и т. д.

Галерея

См. также

• Рукоятка (механизм)
• Кинематическая схема
• Четырехзвенный рычажный механизм
• Ручной насос
• Уравнения движения поршня
• Поршневой двигатель
• Паровой двигатель с качающимся цилиндром
• кулиса
• Крейцкопф

В этой статье использованы материалы из статьи Википедии «Кривошипно-ползунковая связь», выпускаемая под Лицензия Creative Commons Attribution-Share-Alike 3. 0. есть список всех авторы в Википедии

Кривошипно-шатунный механизм — PDFCOFFEE.COM

Кинематика кривошипно-кривошипного механизма Michael Kearney 40274982 Члены группы: Д. Поттер, Пирло, М. Бонавентура. Дата

просмотров 168 Скачиваний 18 Размер файла 2 МБ

Отчет DMCA / Copyright

СКАЧАТЬ ФАЙЛ

Рекомендованные истории

---

Предварительный просмотр

---

Кинематика кривошипно-шатунного механизма Майкла Кирни 40274982

Члены группы: Д. Поттер А. Пирло М. Бонавентура

Дата эксперимента: 15 августа 2005 г.

1

Резюме В этом отчете представлены результаты теоретического и экспериментального исследования одноцилиндрового четырехтактного двигателя внутреннего сгорания. . Разработано теоретическое выражение для смещения поршня в зависимости от угла поворота коленчатого вала. Результаты этого выражения согласуются с экспериментальными измерениями с точностью до 3,3% хода поршня. Также измерялись моменты открытия впускных и выпускных клапанов относительно движения поршня. Оба клапана открыты одновременно при угловом смещении коленчатого вала на 20°, когда поршень находится вблизи верхней мертвой точки между тактами впуска и выпуска.

2

Содержание 1 Введение

4

2 Теория 2.1 Четырехтактный цикл . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 Кинематика кривошипно-кривошипного механизма. . . . . . . . . . . . .

4 4 5

3 Apparatus

6

4 Процедура

7

5 Результаты и обсуждение

6 Выводы

13

Приложения

14

Appaltus.0011

14

B Экспериментальные данные

15

C, полученные экспериментальными данными

20

3

1

Введение

Целью слайдера является преобразование вращательное движение коленчатого вала. Одним из распространенных применений этого механизма являются двигатели внутреннего сгорания. Первая цель этого эксперимента состоит в том, чтобы исследовать и сравнить теоретическую кинематическую связь между смещением поршня и углом поворота коленчатого вала с измеренной для одноцилиндрового двигателя. Другая цель состоит в том, чтобы исследовать четырехтактный цикл, одновременно наблюдая за движением поршня и клапанов.

2

Теория

2.1

Четырехтактный цикл

Двигатель внутреннего сгорания работает за счет сжигания небольшого количества высокоэнергетического топлива, такого как нефть, и использования выделяемой энергии для привода вала. Четырехтактный цикл сгорания, разработанный Николаусом Отто в 1867 году, обычно используется в бензиновых двигателях внутреннего сгорания.

Рисунок 1: Цикл четырехтактного двигателя. Воспроизведено из руководства по двигателю [1]. Четыре такта цикла Отто показаны на рисунке 1. Это: Впуск: впускной клапан открыт, и поршень движется вниз, всасывая смесь топлива и воздуха в цилиндр. 4

Сжатие: Оба клапана закрыты, и поршень движется вверх, чтобы сжать топливно-воздушную смесь. Свеча зажигания срабатывает непосредственно перед тем, как поршень достигает верхней мертвой точки (положения, в котором поршень достигает своего максимального вертикального положения). Это инициирует воспламенение смеси. Мощность: Снова оба клапана закрыты. Горячие газы за счет сгорания топливно-воздушной смеси толкают цилиндр вниз. Шатун передает это прямолинейное движение поршня во вращательное движение коленчатого вала. Таким образом, крутящий момент, прикладываемый к коленчатому валу, можно использовать для привода механизма, например лезвий газонокосилки. Выхлоп: выпускной клапан открывается, и движение поршня вверх выталкивает выхлопные газы из цилиндра. Примечание. Терминология, используемая для описания «четырех ударов», различается в разных источниках [1] [3].

2.2

Кинематика кривошипно-ползункового механизма

Кривошипно-ползунковый механизм, показанный на рис. 2, представляет собой кинематический механизм. Смещение поршня от верхней мертвой точки x можно определить исходя из геометрии механизма с точки зрения длины шатуна L и кривошипа R, а также угла поворота кривошипа θ. Исходя из геометрии и учитывая, что θ = ϕ = 0, когда x = 0, x можно выразить как

x = R — R cos (θ) + L — L cos (ϕ).

(1)

Рис. 2: Кривошипно-ползунковый механизм. Также из геометрии видно, что L sin(ϕ) = R sin(θ)

(2)

и 2

2

[L cos(ϕ)] = L2 − [L sin(ϕ)] .

5

(3)

Замена L sin(ϕ) из уравнения 2 в уравнение 3 оставляет θ единственной переменной в правой части выражения, 2

2

[L cos(ϕ )] = L2 − [Rsin(θ)] .

(4)

Уравнение 4 можно подставить в уравнение 1, чтобы получить кинематическое уравнение кривошипно-шатунного механизма (уравнение 5), q 2 x = R − R cos(θ) + L − L2 − [R sin( θ)] . (5) Уравнение 5 затем можно изменить, введя другой параметр, n, отношение длины шатуна, L, к радиусу коленчатого вала, R, как    s ¶2  µ  sin θ  x = R 1 − cos θ + n 1 − 1 − , (6)   n, где

л. (7) R Уравнение 6 представляет собой кинематическое уравнение кривошипно-ползункового механизма, приведенное в практическом руководстве [2]. Значения параметров R и n определяются путем измерения двигателя Briggs & Stratton. n=

3

Аппарат

В этом эксперименте изучался одноцилиндровый четырехтактный двигатель Briggs and Stratton. Вид двигателя сбоку показан на рис. 3. Вид двигателя сверху, на котором крупным планом показаны цилиндр, поршень и клапаны, показан на рис. 4. Головка снята, и установлены циферблатные индикаторы. для измерения смещения впускных и выпускных клапанов. Поршень и цилиндр также доступны для измерения. Транспортир прикреплен к коленчатому валу для облегчения измерения угла поворота коленчатого вала. Технические характеристики двигателя: • Максимальная мощность 3 л.с. • Рабочий объем 127 куб.см • Номер модели: 81232 • Тип: 0209-01 • Код: 703 • № по каталогу машиностроения: M2820 • Модификации: – Головка снята, что позволяет получить доступ к поршню и клапанам. – Установлен циферблатный индикатор для измерения смещения клапанов. 6

Рис. 3. Двигатель Briggs & Stratton, использовавшийся на практике. Показаны модификации. – На коленчатом валу установлен транспортир с углом обзора 360°, позволяющий измерять угол поворота коленчатого вала. Измерения проводились с помощью этого прибора • Индикатор часового типа: производства Mercer, Англия Разрешение: 0,01 мм • Штангенциркули: производства Tricle Номер модели: P02270108 Идентификационный номер: 4051904 Разрешение: 0,02 мм • 360◦ Транспортир: Универсальный школьный транспортир Разрешение: 0,5◦

4

Процедура

Эксперимент выполнялся в следующей последовательности: 1. Диаметр цилиндра измерялся штангенциркулем.

7

Рис. 4. Вид сверху на двигатель, хорошо видны поршень, цилиндр и клапаны. 2. Внутренний диаметр большого и малого концов шатуна (Dбольшой и Dмалый на рис. 5 соответственно) и размер F (также показанный на рис. 5) были измерены штангенциркулем. Эти числовые значения были подставлены в уравнение 8 для определения кинематической длины шатуна. 1 L = F − (Dбольшой + Dмалый ) (8) 2 3. Кривошип был расположен так, что поршень находится в верхней мертвой точке, между тактами выпуска и впуска. Затем с помощью штангенциркуля измеряли смещение поршня от верхней части цилиндра. 4. Кривошип был повернут на 15° против часовой стрелки, и новое перемещение поршня было измерено с помощью штангенциркуля и записано в бортовой журнал. Этот шаг повторялся с шагом 15°, пока не был завершен один полный цикл (поворот на 360°). 5. Шаги 3 и 4 были повторены дважды, и были рассчитаны средние значения этих измерений. Кинематическая длина кривошипа R затем определялась из средних измерений с использованием уравнения 9.. R=

1 2

( x|НМТ − x|T DC )

Здесь xT DC — удлинение поршня в ВМТ, xНМТ — удлинение поршня в НМТ, а

8

(9 )

Рис. 5: Эскиз шатуна с размерами. R — кинематическая длина кривошипа. 6. Кривошип был возвращен в верхнюю мертвую точку между выпускным и впускным клапанами. Циферблатный индикатор располагался над впускным клапаном, и показания циферблатного индикатора записывались в бортовой журнал. 7. Рукоятку повернули на 10° против часовой стрелки и зафиксировали измерение на циферблатном индикаторе. (Примечание: необходимо скорректировать показания циферблата для начального смещения. Это было сделано путем вычитания показаний на циферблате, когда клапан был полностью закрыт, из других показаний (см. Таблицы 4 и 5). Этот шаг был повторяется с шагом 10◦, пока не будет завершен один полный цикл (720◦ вращения) 8. Затем шаги 6 и 7 повторяются для выпускного клапана.

5

Результаты и обсуждение

На рис. 6 показаны смещения поршня и клапанов в зависимости от углового смещения коленчатого вала от верхней мертвой точки (исходные данные, использованные для построения этого графика, приведены в Приложении B). . Рабочий объем поршня измеряется от положения верхней мертвой точки, а рабочий объем клапана измеряется от полностью закрытого положения. Он показывает, что впускной клапан открывается преимущественно при каждом втором ходе поршня вниз (увеличение рабочего объема поршня), а выпускной клапан открывается преимущественно при каждом втором ходе поршня вверх. Ход вверх при открытом выпускном клапане предшествует ходу вниз при открытом впускном клапане. Отмечается, что клапаны открываются 9

непосредственно перед и закрыть сразу после изменения направления поршня. Впускной клапан открывается за 20° до такта впуска и закрывается за 40° во время последующего хода вверх. Выпускной клапан открывается за 40° до такта выпуска и закрывается сразу после ВМТ между тактами выпуска и впуска (смещение выпускного клапана в ВМТ составляет 0,07 мм). И впускной, и выпускной клапаны открыты приблизительно на 20°, включая верхнюю мертвую точку.

Цикл четырехтактного двигателя — смещения клапанов и поршней 50

40

30

20

10

0

−10 −100

0

100

200

300

400

500

600

700

800

Угол поворота коленчатого вала от ВМТ (°) Теоретическое смещение поршня

Измеренное смещение поршня

Смещение впускного клапана

Смещение выпускного клапана

Рис. 6: Смещение поршня и клапана за весь четырехтактный цикл. Теоретическая кривая смещения поршня также показана на рисунке 6. Параметры R и n в уравнении 6 были определены на основании измерений (см. дополнительные сведения в приложениях A и C) и составляют 22,45 мм и 3,54 соответственно. Когда эти значения подставлены в уравнение 6, теоретическое перемещение поршня может быть выражено как    s µ ¶2   sin θ  . x = 22,45 1 — cos θ + 3,54 1 — 1 — (10)   3,54 На рис. 6 показано, что измеренное смещение поршня очень хорошо соответствует теоретической кривой. Максимальная разница между теорией и измерением составляет 1,5 мм. Это соответствует 3,3% хода поршня. В данных присутствует очевидная погрешность, так как большинство измерений приходится на правую часть теоретической кривой смещения поршня. Более внимательное рассмотрение рис. 6 позволяет оценить это смещение примерно в 4 ◦ − 5 ◦ . Наиболее вероятной причиной смещения является смещение нулевого угла транспортира, который используется для измерения углового смещения кривошипа от верхней мертвой точки. Рабочий объем двигателя (рабочий объем) определяется как рабочий объем цилиндра [3]. Длина развертки равна ходу поршня. В этом разница 10

между выходом поршня от верхней мертвой точки (угол поворота коленчатого вала 0° и 360°) до нижней мертвой точки (угол поворота коленчатого вала 180°). Исходя из этого и диаметра цилиндра, рабочий объем двигателя был рассчитан равным 0,126 л. Это близко к рабочему объему, указанному производителем для этого двигателя (0,127 л). На рис. 7 показана головка цилиндра, расположенная сверху цилиндра. Обратите внимание, что дополнительный объем под головкой не входит в объем двигателя [3].

Рисунок 7: Головка двигателя с указанием внутреннего объема. Этот объем не входит в мощность двигателя. Движение поршня (при постоянной угловой скорости кривошипа) близко к простому гармоническому. Это позволяет оценить угол поворота кривошипа, при котором достигается максимальная скорость поршня (при постоянной угловой скорости кривошипа). Максимальная скорость вниз будет иметь место при угле поворота коленчатого вала 90 ◦ , а максимальная скорость подъема будет иметь место при угле кривошипа 270 ◦ , и измерения показывают, что смещения поршня при этих углах кривошипа составляют 24,39 мм и 26,69 мм соответственно. Распределительный вал (используемый для открытия и закрытия клапанов в соответствующее время) вращается с половиной скорости коленчатого вала. Это видно из рис. 6, где видно, что поршень совершает два оборота при одном и том же угловом перемещении кривошипа, при котором кулачки совершают один оборот. Если предположить, что движение впускного клапана может быть аппроксимировано простым гармоническим движением, то скорость и ускорение клапанов могут быть 11

для данной частоты вращения двигателя. Такие расчеты показывают, что при частоте вращения коленчатого вала 3000 об/мин максимальное ускорение, испытываемое клапаном, составляет 112,4 мс-2. Это соответствует примерно 11,5 г.

12

6

Выводы

Кинематическое движение ползуна в кривошипно-ползунковом механизме может быть выражено через длины кривошипа и шатуна и угловое перемещение коленчатого вала. Экспериментальные измерения смещения поршня согласуются с предсказаниями теоретической модели движения поршня с точностью до 3,3% хода поршня. В настоящем эксперименте также наблюдалось смещение между теоретическими и экспериментальными значениями смещения поршня. Это было связано с неправильной установкой нулевого угла транспортира, измеряющего угол поворота кривошипа. Это смещение оценивается как 4 ◦ − 5 ◦ . Впускной клапан был открыт во время такта впуска, а выпускной клапан был открыт во время такта выпуска. Диапазон открытия обоих клапанов выходит за пределы верхней мертвой точки для их соответствующих ходов. Вблизи верхней мертвой точки между тактами выпуска и впуска оба клапана были открыты примерно на 20° и угловой поворот коленчатого вала. Увеличенный диапазон открытия клапана позволяет большему количеству воздуха поступать во время такта впуска и выходить во время такта выпуска.

13

Приложения A

Аппаратные измерения

Диаметр цилиндра необходим для определения объема цилиндра и мощности двигателя. Его измеряли, взяв среднее значение ряда показаний диаметра под разными углами вокруг цилиндра. Результаты представлены в таблице 1. Среднее значение диаметра составляет 59,8 мм.

Таблица 1: Измерения и расчетные значения диаметра цилиндра. Диаметр цилиндра Диаметр (мм) Размер 1 60 Размер 2 59.65 Измерение 3 60.02 Измерение 4 59.6 Среднее значение 59.8 Изменение 0.42 Для определения кинематической длины шатуна L необходимо измерить размеры SmallD, LargeD и F шатуна (см. рис. 5). Эти измерения приведены в Таблице 2. Таблица 2: Измерения, сделанные для определения длины шатуна. Общая длина (мм) Меньший диаметр (мм) Размер 1 98,04 25,1 Размер 2 97,98 25,14 Размер 3 97,96 25,16 Размер 4 98,02 25,26 Средний размер 98 25,16 Вариация 0,04 0,1

14

Больший диаметр (мм) 11,88 11,88 11,62 12,3 11,92 0,38

B

Рейские экспериментальные данные

Сырьи и корректированные измерения дисплета Piston показаны в таблице 3 и скорректируются. замеры рабочего объема впускного и выпускного клапанов приведены в таблицах 4 и 5 соответственно.

Угол поворота (◦ ) 0 15 30 45 60 75 90 105 120 135 150 165 180 195 210 225 240 255 270 285 300 315 330 345 360

Table 3: Piston Displacement Piston Extension (mm) M1 M2 M3 Average Max 0 0 0 0 0. 86 0.80 0.90 0.85 3.12 3.24 3.28 3.21 7.58 7.32 7.36 7.42 12.72 12.46 12.46 12.55 18.28 18.08 18.20 18.19 24.7 24.26 24.22 24.39 30.00 29.94 30.40 30.11 35.20 34.96 35.24 35.13 39.28 39.12 39.32 39.24 41.90 42.08 42.16 42.05 44.14 43.94 43.78 43.95 44.98 45.00 44.72 44.90 44.34 44.30 44.36 44.33 42.86 42.66 42.72 42.75 40.30 40.10 40.40 40.27 36.46 36.56 36.56 36.52 32.32 32.08 32.10 32.16 26.68 26.72 26.68 26.6920.06 20.84 20.84 20.58 14.80 14.82 15.20 14.94 9.78 9.60 9.70 9.69 4.80 5.04 4.82 4.89 1.68 1.88 1.58 1.71 0 0 0 0

15

Variation 0 0.05 0.09 0.16 0.17 0.11 0.31 0.29 0.17 0.12 0.15 0.19 0.18 0.03 0.11 0.17 0.06 0.16 0.03 0.52 0,26 0,09 0,15 0,17 0

Таблица 4: Расширение клапана впускного клапана на полном четырех ударе по угла рукавого цикла 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 230 240 250 260 280 280 290 300 310 320 330 340 350 360 370 380 390 400 410 420

raw measurement(mm) 1.46 2.06 2.68 3.21 3.66 4. 04 4.3 4.51 4.64 4.69 4.7 4.69 4.67 4.59 4.4 4.15 3.79 3.38 2.87 2.29 1.66 1.21 0.96 0.9 0.9 0.9 0.92 0.82 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65

16

corrected measurement(mm) 0.81 1.41 2.03 2.56 3.01 3.39 3.65 3.86 3.99 4.04 4.05 4.04 4.02 3.94 3.75 3.5 3.14 2.73 2.22 1.64 1.01 0.56 0.31 0.25 0.25 0.25 0.27 0.17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Продолжение на следующей странице

Угол кричата 430 440 450 460 470 480 490 500 510 520 530 540 550 560 570 580 590 600 610 620 640 650 660 670 680 690 700 710 720

Измерение сыра 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,65 0,69 0,75 1,01 1,44

17

Скорректированное измерение (мм) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,0002 0 0 0 0 0 0 0 0,04 0,1 0,36 0,79

Таблица 5: Выдвижение выпускного клапана за полный четырехтактный угол поворота коленчатого вала 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330 340 350 360 370 380 390 400 410 420

Измерение сыра 0. 48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48 0.48

18

corrected measurement(mm) 0.07 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Продолжение на следующей странице

Угол кривошипа 430 440 450 460 470 480 490 500 510 520 530 540 550 560 570 580 590 600 610 620 640 650 660 670 680 690 700 710 720

Измерение сыра. 1.71 2.32 2.85 3.28 3.64 3.88 4.07 4.17 4.2 4.2 4.2 4.14 4.03 3.82 3.53 3.13 2.72 2.16 1.57 0.97 0.55

19

corrected measurement(mm) 0 0 0 0 0 0 0 0.13 0.61 1.23 1.84 2.37 2.8 3.16 3.4 3.59 3.69 3.72 3.72 3,72 3,66 3,55 3,34 3,05 2,65 2,24 1,68 1,09 0,49 0,07

C

Полученные экспериментальные данные

Длина шатуна L определяется с помощью уравнения 8 и средних измерений в таблице 2. Расчетная длина шатуна составляет 79,46 мм. Кинематический радиус кривошипа R определяется путем деления вдвое смещения поршня из положения его верхней мертвой точки в положение его нижней мертвой точки. Таблица 3 показывает, что это расстояние составляет 44,90 мм. Следовательно, кинематический радиус кривошипа составляет 22,45 мм. Отношение длины шатуна к радиусу кривошипа, n(= L/R = 790,46/22,45), рассчитывается как 3,54. Вместимость цилиндра рассчитывается по формуле объема цилиндра πD2·ч. (11) 4 Высота цилиндра h определяется разностью смещения поршня между верхней и нижней мертвыми точками. Как указано выше, это было измерено как 44,90 мм. Измерение диаметра поршня записано в Приложении А как 59,8 мм. Используя уравнение 11, емкость цилиндра рассчитывается как 126 см3 или 0,126 л. В =

В таблице 6 показаны углы поворота коленчатого вала, при которых открываются и закрываются впускные и выпускные клапаны. Таблица 6: Угол поворота коленчатого вала, при котором клапаны открываются и закрываются Клапан открывается закрывается ВХОД −20° (700°) 220° ◦ ВЫПУСК 500 720° (0°)” В первом приближении движение открытия и закрытия впускного клапана может можно записать в виде · µ ¶¸ 1 πt y = ymax 1 − cos , (12) 2 T где y – смещение клапана из закрытого положения, ymax – максимальное смещение клапана, t – время, T – время, в течение которого впускной клапан открыт. Уравнение 12 можно продифференцировать по времени, чтобы получить выражение для скорости впускного клапана, а затем снова продифференцировать по времени, чтобы получить выражение для ускорения клапана. Скорость 9Таким образом, 0011

20

и ускорение клапана задаются уравнениями 13 и 14 соответственно. ¨ = ymax cos (14) 2 T T Из таблицы 6 видно, что впускной клапан открыт при угловом смещении коленчатого вала 240 ◦ . Период времени, которому это соответствует, затем можно рассчитать по уравнению 15. 60 240 ◦ N 360 ◦ где N — скорость вращения коленчатого вала в об/мин. T =

(15)

Если частота вращения коленчатого вала 3000 об/мин, то N = 3000 и из уравнения 15, впускной клапан будет открыт в течение T = 13,3 мс. Максимальное смещение впускного клапана можно найти из таблицы 4 и оно равно ymax = 4,05 мм. Максимальное ускорение можно рассчитать по уравнению 14, чтобы быть y¨max =

ymax π 2 . 2T 2

(16)

Подставляя эти значения для T и ymax в уравнение. 16 дает расчетное максимальное ускорение впускного клапана 112,4 м/с (11,5 g).

21

Ссылки [1] Инструкции по обслуживанию и ремонту Briggs & Stratton. 1976 [2] Ми, Д., Лабораторный лист: Кинематика механизмов. Отделение машиностроения Университета Квинсленда. 1997. [3] Пулкрабек, В. В., Инженерные основы двигателя внутреннего сгорания, Прентис Холл, Нью-Джерси, 19.97.

22

Механоанализатор — Робоанализатор

MechAnalyzer ® — это программное обеспечение на основе 3D-моделей, разработанное для эффективного преподавания и изучения курсов, связанных с механизмами. Это развивающийся продукт, разработанный в лаборатории мехатроники кафедры машиностроения ИИТ Дели, Нью-Дели, Индия, под руководством профессора С.К. Саха. Он находится в свободном доступе для академического использования.

Изучение различных плоскостных и пространственных связей рассматривается в разделе «Проектирование механизмов», который является базовым курсом, преподаваемым в учебной программе. машиностроения. Студенты изучают кинематические и динамические уравнения для анализа различных типов механизмов. Компьютерный подход к решению эти уравнения становятся неизбежными, когда число уравнений увеличивается и также для быстрого и лучшего понимания через визуализацию. В настоящее время, есть много коммерчески доступных программ, которые могут помочь студентам в этом иметь значение. К сожалению, для обучения студентов требуется значительное количество времени. для того, чтобы использовать их.

Обратная связь: MechAnalyzer находится в стадии разработки. Если у вас есть какие-либо вопросы или предложения/отзывы, мы будем рады услышать ваши ценные отзывы.

MechAnalyzer — это бесплатное программное обеспечение, разработанное для моделирования и анализа уже загруженных в него механизмов, что позволяет сократить время и усилия, необходимые для начала работы с ним. Программное обеспечение было разработано на C# и использует OpenGL/OpenTK для визуализации. Поскольку это программное обеспечение находится в активной разработке, скриншот текущей версии показан справа. Все версии, которые были выпущены до сих пор, перечислены ниже.

Особенности: Около 10 механизмов Прямая кинематика Анимация с кривой сопряжения Графики

Минимальные системные требования: Процессор: не менее 1,5 ГГц ОЗУ: не менее 512 МБ

Загрузить:

MechAnalyzer Version 6 (20210811)
Загрузить программное обеспечение
Новые возможности: Улучшения в основном модуле, добавление нескольких ошибок0011

MechAnalyzer Версия 5 (20180203)
Загрузить программное обеспечение

Новые функции: Анализ скорости мгновенным методом (IC) был добавлен в модуль векторной диаграммы. Профиль CAM и профиль зубчатого колеса с чертежом и моделированием представлены в виде двух новых модулей

MechAnalyzer Версия 4.1 (20161223) Загрузить ПО

Новые функции: Добавлено больше механизмов, включая Женевский механизм. Добавлен модуль Statif Force Analysis (SFA).

MechAnalyzer Версия 4 (20150902) Загрузить ПО Загрузить Руководство пользователя

Новые функции: Добавлены графики для кинематического анализа. Добавлен новый модуль скорости и ускорения (VAD) с чертежами скорости и ускорения для распространенных планарных механизмов

MechAnalyzer Версия 3 (20150824) Загрузить ПО Загрузить Руководство пользователя

Новые возможности: Полное обновление программного обеспечения. Пользовательский интерфейс похож на RoboAnalyzer. Добавлено около 10 механизмов с Forward Kinematics.

MechAnalyzer Версия 2 (20150318) Загрузить ПО

Новые возможности: Добавлен пятизвенный механизм, инверсии и специальные механизмы четырехзвенных и ползунковых кривошипных механизмов

MechAnalyzer Версия 1 (20131229) Загрузить программное обеспечение Загрузить руководство пользователя

Новые функции: Первый выпуск с прямой кинематикой и обратной динамикой четырехзвенного механизма и ползунково-кривошипного механизма с возможностью графического построения

Учебное пособие:
Ниже приведено очень краткое руководство по началу работы с MechAnalyzer V2. Пользователям также рекомендуется ознакомиться с Руководством пользователя, доступным в разделе «Загрузить».

Кредиты:

• Проф. С.К. Саха (ИИТ Дели): Надзор
• Г-н Радживлочана Г. Читтавадиги (доцент, Инженерная школа Амрита Бангалор): Наставничество и координация
• Г-н Шамант Хампали (2013 г., летний стажер в NITK Surathkal): Версия 2, включающая кинематику и динамический анализ четырехзвенных, кривошипно-кривошипных и пятизвенных механизмов
• Г-н Ракшит Локеш (2014 г., летний стажер из NITK Surathkal): Версия 3 с прямой кинематикой около 10 механизмов
• Г-н Рохит Кумар (2015 и 2016, летний стажер в NITK Surathkal): Дополнительные механизмы и динамическое моделирование четырехзвенного механизма в версиях 4 и 4.1.
• Г-н Сачин Кумар Верма (2015 и 2016, летний стажер в NITK Surathkal): модуль диаграммы ускорения (VAD) и модуль анализа статической силы (SFA) в версиях 4 и 4.