Что значит «категория В», попадают ли ограниченно годные мужчины под частичную мобилизацию: кого призывают на военные сборы в сентябре 2022 года — 26 сентября 2022

Все новости

Отдых у воды бывает разным: подводим итоги недели в фотографиях

В ЧВК «Вагнер» заявили о приостановке набора наемников

В Волгограде выставлен на торги еще один автобус скандальной «Дианы Тур»

«Меня обидела Екатерина Мизулина»: в Волгограде ищут бомбу в торговом центре и аэропорту

Зеленский назвал условие для мирных переговоров, а на Кубани прогремел взрыв: новости СВО за 2 июля

Обед вместо подтяжки: добавьте эти 6 продуктов в рацион — и не узнаете себя в зеркале

Пенсионер строит сказочный дом из мусора — взгляните, как он выглядит

«Начинаешь бояться, что больше никогда не сможешь увидеть родные места»: бывшая радиоведущая из России — о жизни в Италии

Виноват ледниковый период или лихие 90-е? Биолог рассказал про загадку озера Лотосов под Волгоградом

Оба на красный пролетели: жуткая авария на Второй Продольной в Волгограде попала на видео

Налетай, подешевело: в Волгограде с большим дисконтом продают здание туристического вокзала

В Волгограде на Второй продольной фура раздавила две легковушки — видео

Трассу под Волгоградом парализовала пробка из-за мелкой аварии

«После смены в супермаркете сажусь в такси и говорю водителю: «Вам пакет надо?»» Читатели рассказали о самых неловких ситуациях

Платные парковки Волгограда появились на «Яндекс. Картах»

Избавляемся от луковой мухи, паутинного клеща и тли: боремся с вредителями без химии (дешево и сердито)

«Доллар дорожал всегда и будет дорожать дальше»: инвестор рассказал, как спасать рубли от инфляции в Волгограде

Возможны пробки: в Волгограде из-за коммунальной аварии перекрыли Вторую Продольную

«Наша тенденция — это тенденция неприятия жизни, тупое ожидание конца». Режиссер Сергей Урсуляк — о нужных героях и мире, в котором мы живем

Июль они точно не переживут: засыхающие в центре Волгограда туи сняли на видео

Под Волгоградом школьник на мотоцикле сбил двух девочек-подростков

Больше, чем в табачном дыме: ученые обнаружили, что газовые плиты выделяют бензол, способный вызвать рак

«Микроб» не уступил: полиция Волгограда рассказала подробности жесткой аварии на Второй Продольной

В Волгограде переделанная под жилье прачечная подорожала на миллион

«Я скучаю по людям и московскому метро». Студентка из России рассказала о своей новой жизни в Нидерландах

«В Афганистане их ждут талибы и смерть»: полиция Волгоградской области отказала в убежище многодетной семье

Лето, ты проснулось: смотрим прогноз погоды в Волгограде на первую неделю июля

Там куча спасателей, скорая: жесткая авария на проклятом перекрестке в Волгограде

Киев ввел санкции против сотен российских заводов — эта и другие новости СВО за 1 июля

В Волгограде 30 лет назад был открыт Мемориально-исторический музей. Смотрим, каким он был, по фото из частной коллекции

«Шок от звуков и взрывов»: поселок под Волгоградом проснулся в панике от салюта со двора празднующего чиновника

Риски возрастают: ученые выяснили, как ночной шум за окнами влияет на продолжительность жизни

«Она тухла гектарами»: эксперты рассказали, когда ждать клубнику в Волгограде и почему она такая дорогая

Мечтал похудеть и влюбиться. Как жил и погиб самый толстый мальчик в мире и первый сумоист Кабардино-Балкарии

«Ты так всё слопаешь!» Как готовить орешки со сгущенкой по-советски и почему это всегда праздник

Ветка пробила машину, белье улетело: на Волгоград обрушился сильный ветер

Проверьте, как вы помните советское кино: тест для самых внимательных

Под Волгоградом двухлетний мальчик погиб от угарного газа. Его мать признали виновной

«Девчонка его долго оплакивала»: в Волгограде 17-летний подросток выпал из окна после выпускного вечера

Все новости

В соответствии с законодательством РФ подлежат призыву рядовые и сержанты до 35 лет, младшие офицеры до 50 лет, старшие — до 55 лет

org/Person»>Фото: Наталья Бурухина / NN.RU

Поделиться

В указе Владимира Путина о частичной мобилизации никак не упомянуты категории военнослужащих, которые это коснется. Юристы утверждают, что если понимать этот указ буквально, то мобилизации подлежат абсолютно все. Хотя официальные лица неоднократно заявляли, что будут мобилизовать только тех, кто служил в армии и/или имеет боевой опыт, однако документально это нигде не зафиксировано. Вместе с экспертами мы попробовали разобраться, что значит «ограниченно годный» и насколько этим людям нужно быть готовыми встать «под ружье».

В военном билете «категория В» значит, что призывник ограниченно годен к военной службе. От службы по призыву в мирное время он освобожден. Также граждане с данной категорией освобождаются от призыва на военные сборы. Их зачисляют в запас.

В военном билете свою категорию можно посмотреть на одиннадцатой странице. Запись о самой болезни, по которой присвоили категорию В призывнику, не указывается. Это врачебная тайна.

Но, как правило, под категорию В попадают граждане с рядом специфических диагнозов. Например, с незначительными психическими нарушениями и (или) отчетливыми вредными для психического или физического здоровья последствиями болезней. В категорию зачисляют тех, у кого есть болезни кожи и подкожной клетчатки: хроническая крапивница, рецидивирующие отеки Квинке, распространенный псориаз.

Туда же идут те, у кого инфекционные болезни, которые не поддаются лечению. К примеру, излеченный туберкулез легких, активный в закрытой форме, без распада ткани легких, первичный, вторичный и скрытый сифилис, кандидоз внутренних органов. Вся информация о категории есть в «Расписании болезней».

В указе президента сказано, что призываются граждане запаса. Состав запаса определяется 52-й статьей Федерального закона «О воинской обязанности». Со списком тех, кто зачисляется в запас, можно ознакомиться тут.

Примечательно, что из текста указа следует, что подлежат призыву «запасники», то есть это люди с категориями А, Б, В. Хоть устно Владимир Путин в обращении и сказал, что подлежат частичной мобилизации в первую очередь те, кто прошел военную службу, но в тексте указа это не конкретизировано.

Для подготовки к военной службе граждане, пребывающие в запасе, могут призываться на военные сборы. Они регулируются статьей № 54 Федерального закона «О воинской обязанности и военной службе».

Проведение военных сборов осуществляется, согласно закону, только для подготовки к военной службе. В иных целях их проведение не допускается.

Военные сборы подразделяются на учебные сборы, сборы по проверке боевой и мобилизационной готовности воинских частей и военных комиссариатов.

— Продолжительность военных сборов, место и время их проведения определяются Министерством обороны Российской Федерации либо иным федеральным органом исполнительной власти или федеральным государственным органом, в которых настоящим федеральным законом предусмотрена военная служба, — гласит закон.

Продолжительность военного сбора не может превышать двух месяцев. Общая продолжительность военных сборов, к которым привлекается гражданин за время пребывания в запасе, за исключением граждан, пребывающих в резерве, не может превышать 12 месяцев. Общая продолжительность сборов, к которым привлекается гражданин из резерва в течение срока контракта о пребывании в резерве, определяется Положением о порядке пребывания граждан Российской Федерации в мобилизационном людском резерве, утверждаемым Правительством РФ.

Корреспондент NN.RU задал вопрос про сборы и частичную мобилизацию категории В полковнику в отставке, кандидату военных наук и военному эксперту Виктору Литвиненко.

— Сейчас для того, чтобы отправить человека туда, на спецоперацию, даже действующий офицер обязательно проходит медобследование. В результате этого обследования если по здоровью он не проходит, то он не подлежит отправке. В этом плане очень четкий и жесткий отбор. Что касается сборов — на сборы могут пригласить категорию В. Потому что сборы — это плановое мероприятие, связанное с подготовкой страны к случаям, как у нас сейчас. На этих сборах люди проходят подготовку. Они заключаются в том, что они по роду войск и по своей специальности проходят те или иные занятия. После сборов, которые, как правило, проходят при воинских частях, на полигонах, с техникой и вооружением, завершают работу. Им делается учетная запись в их военкоматах в личном деле. Это не значит, что после этих сборов его обязательно отправят туда, куда необходимо, — сообщил Литвиненко.

По поводу граждан, которых, скорее всего, призовут в первую очередь, он сказал:

— Сейчас будут направлять людей, специалистов, которые необходимы. Это те люди, которые в боевых действиях участвовали, являются специалистами. Ну, например, механик-водитель, артиллерийский наводчик, командир артиллерийской установки и т. д. И то они будут проходить не сразу в бой. С ними будет проходить слаживание. Сейчас нет необходимости в том, чтобы сразу человека взять с мирной жизни и бросать в бой. Потому что это сразу будет просто жертва.

Также Литвиненко отметил, что повестка не всегда означает моментальное направление в зону боевых действий:

— Я сейчас знаю, что по определенным ребятам пошли повестки. Но это не значит, что их сразу сейчас заберут и будут бросать в бой. Этого бояться не надо. Ну а защищать страну надо. Родину защищать необходимо. Иначе какие мы граждане этой страны?

За уточнением порядка призыва мы обратились к секретарю СПЧ Александру Точенову. Он рассказал, что значит «ограниченно годный» и кого должны призвать в первую очередь.

— Призывают граждан из запаса. Люди отслужившие находятся в запасе. Люди, получившие по образованию военно-учетную специальность. Как раз будут призываться те, кто служил по контракту, те, кто имеет соответствующую военную специальность, необходимую для выполнения задач. Именно они будут призываться. И те, кто имеет боевой опыт. Есть категории ограничений. Не годен к службе в мирное время, ограниченно годен в военное время. Есть такие формулировки. Сначала призывают здоровых, сильных. Но у нас ограниченная мобилизация, частичная мобилизация. Указ так называется. Конкретное число есть, сколько будет призвано. Не надо волноваться за тех, кто имеет освобождения по медицинским показаниям, — сообщил Точенов.

Те, что не проходят по медицинским показаниям, по его словам, в первую очередь призваны не будут:

— У нас нет всеобщей мобилизации. У нас частичная. Ведь Шойгу конкретно сказал, что есть 25 миллионов тех, кого можно призвать, но призывают 300 тысяч. Чуть больше одного процента.

Однако, как сообщил нашим коллегам из IRCITY.RU военком Иркутской области, категорию В всё же могут призвать — но в последнюю очередь.

новость из сюжета

Подпишитесь на важные новости о спецоперации на Украине

Напомним, ранее мы писали о том, кого будут призывать во время частичной мобилизации. В соответствии с российским законодательством подлежат призыву рядовые и сержанты до 35 лет, младшие офицеры до 50 лет, старшие — до 55 лет.

По теме

• 11 мая 2023, 13:07

  Могут ли призвать на военные сборы, а отправить в зону СВО? Отвечают юристы

• 16 мая 2023, 11:20

  Отправят ли призванных на военные сборы в зону спецоперации? Ответили в Госдуме

• 17 мая 2023, 10:00

  В России объявили военные сборы.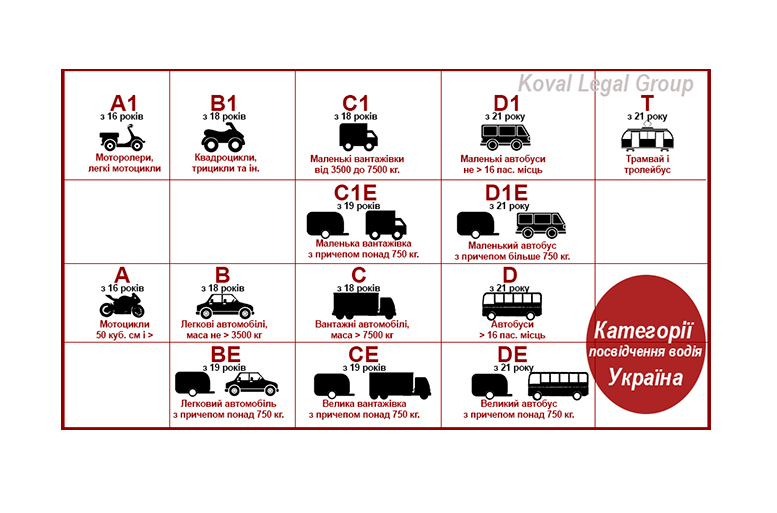 Кого на них призвать не могут — объяснение в трех картинках

• 08 июня 2023, 08:00

  Судимым и ограниченно годным россиянам хотят разрешить службу по контракту во время мобилизации. Зачем это нужно?

• 11 мая 2023, 08:00

  В России снова объявили военные сборы. Кого призовут, на сколько и что будет тем, кто не явится

Алена Дорофеева

корреспондент NN.RU

Специальная военная операцияПризывная кампанияЧастичная мобилизация

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ31

Читать все комментарии

Гость

Войти

Новости СМИ2

Новости СМИ2

Категории годности к военной службе: что обозначают

СОДЕРЖАНИЕ СТАТЬИ:

• Как присваивается разряд годности?
• Где в военном билете указана категория годности?
• Если категория присвоена, можно ли ее изменить?

 

Категории годности существуют для того, чтобы определять физическое состояние призывников, которое непосредственно определяет их возможность служить в армии.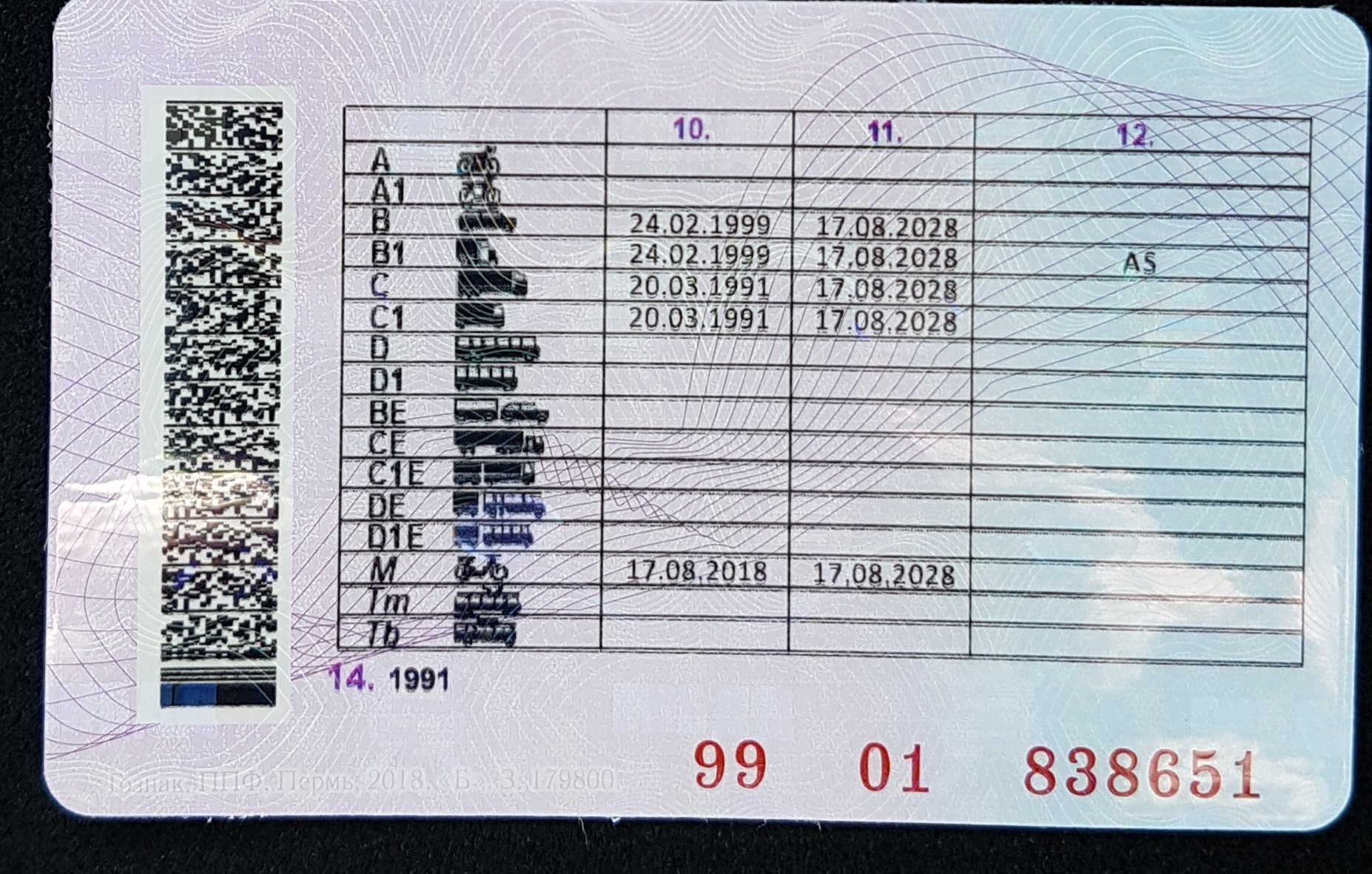 Чтобы получить категорию, нужно пройти медосвидетельствование. Комиссия из докторов решит, каково состояние юноши на момент освидетельствования.

Все категории годности

Военных категории годности всего 5. Из них только категория годности «Д» присваивается тем, кто наверняка не годен к несению военной службы. В противоположность ей категория годности «А» присваивается только годным к военной службе, без всяких оговорок.

Другие категории расшифровываются так:
категория годности «Б» — годен, но с небольшими ограничениями:
категория годности «В» — ограниченно годен;
категория годности «Г» — временно не годен.

Как присваивается разряд годности?

Призывник получает категорию, будучи приглашенным в военный комиссариат на медицинское освидетельствование, которое проводят в рамках призывной комиссии.

В комиссии присутствуют доктора ведущих специальностей. Это: хирург, стоматолог, психиатр, офтальмолог, оториноларинголог, терапевт и невролог. Каждый только в рамках своей области медицины определяет категорию годности, которая присваивается конкретным доктором временно.

Доктора не только осматривают призывника, но и изучают его ранние медицинские документы.

После этой процедуры врач, который возглавляет группу коллег в комиссии, выставляет окончательный разряд годности. Он действует по принципу, что окончательная категория — это самая худшая из тех, что выставлена докторами-специалистами.

Его решение озвучивается и подтверждается призывной комиссией на заседании, устраиваемом после медосвидетельствования.

Если на медкомиссии не могут определить категорию — что дальше?

Бывают ситуации, что со здоровьем призывника не все так очевидно. Но какие бы опытные специалисты не присутствовали на комиссии, конечные выводы о годности они не могут сделать ни на основании меддокументов призывника, ни на основании осмотра молодого человека.

В этом случае призывник направляется в поликлинику или больницу, чтобы пройти там обследование в стационаре или амбулаторно. И уже там врач, который специализируется на конкретном недуге, даст для военкомата свое заключение о годности, которое для комиссии будет являться главенствующим при решении судьбы призывника.

Где в военном билете указана категория годности?

Категория проставляется на странице 13, в разделе формуляра, который называется «Сведения о медицинских освидетельствованиях и прививках» и имеет VI порядковый номер в билете.

Традиционно разряд указывается литерой, то есть буквой из русского алфавита, а за ней следует расшифровка этого обозначения.

Информация о категории есть и на 14 странице формуляра, но там она проставляется после отбытия срочной службы, как итоговый ее показатель.

Если категория присвоена, можно ли ее изменить?

Безусловно, решение, которое принимает о годности призывника военный комиссариат, можно и нужно обжаловать, другой вопрос, готов ли призывник пойти против системы в одиночку.

На обжалование по закону отводится 3 месяца, но за это время призывник может уже попасть в армию и даже принять присягу. И будучи в вооруженных войсках, доказывать свою непригодность еще сложнее, чем на «гражданке». Поэтому важно действовать быстро и компетентно!

Жалоба на решение о присвоении категории является поводом для приостановления отправки на службу. Она направляется в вышестоящую призывную комиссию, а если и та принимает решение не в пользу призывника, то и его реально оспорить, но уже в суде.

Чтобы всем этим заниматься, требуется не только много свободного времени, но и знание законов, поэтому проще, если призывник обратиться к профессиональным юристам, делегировав им полномочия на разрешение этой проблемы.

Каково конкретное значение следующего в определении категории?

$\begingroup$

В теории категорий Аводи категория определяется следующим образом.

Категория состоит из следующих данных:

• Объекты: $A, B, C,\ldots$

• Стрелки: $f,g,h,\ldots$

• Для каждой стрелки $f$ заданы объекты, $$\operatorname{dom}(f),\ \ \operatorname{cod}(f)$$ называется домен и кодовый домен $f$. Мы пишем $f : A → B$ чтобы указать, что $A = \operatorname{dom}(f)$ и $B = \operatorname{cod}(f)$.

• Даны стрелки $f : A → B$ и $g : B → C$, т.е. $\operatorname{cod}(f) = \operatorname{dom}(g)$ дана стрелка $g \circ f : A → C$ называется составным из $f$ и $g$.

• Для каждого объекта $A$ задана стрелка $1_A : A → A$ называется идентификационной стрелкой А.

Эти данные должны соответствовать следующим законам:

• Ассоциативность: $$h \circ (g \circ f)=(h \circ g) \circ f$$ для всех $f : A → B, g : B → C, h : C → D$.

• Единица измерения: $f \circ 1_A = f = 1_B \circ f$ для всех $f : A → B$.

Мои вопросы:

1. Что мы имеем в виду, когда говорим, что категория «состоит из» чего-то? Принадлежат ли функции и объекты категории в каком-то более общем смысле $\in$, как в $\sf{ZFC}$?

2. Предположительно, здесь Аводи говорит о «наборе предметов» и «наборе стрел», но что именно здесь является набором? Это будут сеты? классы? или что-то другое?

3. В чем разница(я) между данными и законами ?

4. Как было сказано в ответе Утконоса Q ниже, я думаю, что мы можем определить категорию как тройку объектов, стрелок и композиции.

   Но тогда нам нужно знать, принимаем ли мы понятие тройки как примитивное понятие. Ибо если нет, то, естественно, возникает вопрос, каково определение тройки?

• теория категорий
• определение
$\endgroup$
12
$\begingroup$

Этот вопрос на самом деле не касается самой теории категорий (хотя теория категорий — это первый предмет, в котором проблема, с которой вы сталкиваетесь, не может быть легко заметена под ковер). 1. и 2. можно с одинаковым успехом задать в теории множеств и базовой алгебре

1. «Каким образом совокупность всех множеств состоит из множеств?»
2. «Что такое коллекции наборов?»

Чуть более тонкое число 3. но его можно задать в алгебре

3. «В чем разница между объявлением группы множеством, снабженным операцией двоичного умножения, так что каждый элемент имеет обратный, и объявлением группы быть множеством, снабженным операцией бинарного умножения и операцией унарной инверсии (обе структуры с соответствующими аксиомами)?»

Ответы на 1 и 2 заключаются в том, что вы должны создать некоторую теорию, которая позволит вам говорить о коллекциях. Стандартная теория делает это с помощью логики первого порядка, в которой каждая формула со свободными переменными является описанием набора (также известного как класс), и эти наборы также могут быть описаны вспомогательными функциями и отношениями.

Теория множеств в таком случае представляет собой определенный набор со вспомогательным отношением, называемым «принадлежностью» ($\in$), которое удовлетворяет определенным аксиомам (например, ZFC). Назовем объекты, составляющие эту коллекцию, устанавливает .

Арифметика Пеано — это еще один набор, называемый натуральными числами, оснащенный обозначенным объектом $0$ и специальной функцией, называемой «преемник», подчиняющейся определенным аксиомам. Это отличается (но связано) с натуральными числами, рассматриваемыми как набор, потому что любой набор определяет набор своих элементов со свойствами, отражающими свойства набора.

Категории вообще представляют собой (вернее, могут быть представлены как) пару наборов в указанном выше смысле (наборов, описываемых формулами со свободными переменными в логике первого порядка), известных как наборы объектов и наборы морфизмов, снабженные вспомогательные функции и отношения между ними (тождество, домен, домен, частично определенная композиция), удовлетворяющие определенным аксиомам (тождество, ассоциативность).

Все усложняется, потому что если у вас также есть теория фиксированных множеств (например, ZFC), то вы можете строить категории как наборы элементов пар множеств, снабженных функциями множеств и отношениями, которые удовлетворяют соответствующим аксиомам. Это будут так называемые

малых категорий. Фундаментальная категория — это категория множеств, потому что традиционная математика строится поверх нее, поэтому вы должны изучать взаимодействие теории множеств (т. е. категории множеств) со всеми другими категориями, обращая внимание на то, какие из них малы и какие большие.

Еще одна сложность заключается в том, что не существует класса всех функций класса, по той же причине не существует набора всех множеств. Но есть класс всех функций класса, областью определения которых является множество, т. е. малый класс. Итак, поскольку категории могут быть большими, при построении категорий и вообще размышлении о них вы должны обращать внимание на вопросы размера , на то, малы ли они (заданы классами элементов некоторого множества или нет).

Людям неудобно работать с этим вручную, поэтому вместо этого они дополняют ZFC «аксиомой вселенных», которая утверждает, что существует набор, все элементы которого образуют совокупность, удовлетворяющую аксиомам ZFC. Такие множества тогда называются малыми, а другие — большими, и тогда вы можете пройти через теорию категорий, не изучая логику первого порядка и лишь наивно используя это расширение ZFC. Делая это, вы больше не имеете категории ВСЕ наборы, а вместо этого работаете с категорией маленькие комплекты.

$\endgroup$
7
$\begingroup$

Сказать, что категория «состоит из данных», означает, что для того, чтобы определить категорию, нужно сообщить читателю именно те данные, которые лежат внутри определения. Например, моноид состоит из следующих данных: множество $M$; бинарная операция $\circ:M \times M \to M$, которая является ассоциативной, т. е. $\circ(g,\circ(h,k)) = \circ(\circ(g,h),k)$ ; и выделенный элемент $e \in M$, называемый тождеством, обладающим свойством $\circ(g,e) = g = \circ(e,g)$ для всех $g \in M$.

Задать моноид $M$ — значит определить все эти вещи одновременно. Таким образом, сказать, из чего состоит категория, значит определить, что составляет категорию. В этом смысле, говоря, что нечто принадлежит категории, мы имеем в виду, что оно является элементом объекта «множество», имеет соответствующий тождественный морфизм в морфизме «множество» и удовлетворяет необходимым тождествам относительно композиции. Здесь нам понадобится некоторое понятие «множества», но подойдет любая теория, с которой вы хотите работать; например, вы можете использовать ZFC, вы можете использовать некоторую теорию множеств, включающую подходящее понятие вселенной Гротендика, в которой каждое «множество», меньшее, чем некоторый фиксированный сильно недостижимый кардинал $\kappa$, является «малым», а любое другое «множество» большая или даже странная модель теории множеств. Прелесть элементарных аксиом теории категорий в том, что они остаются в силе до тех пор, пока ваша теория множеств может обрабатывать количественную оценку и универсальную конкретизацию, необходимую для получения требуемых данных.
Обратите внимание, что мы можем отказаться от понятия примитивной вселенной, скажем, такой как категория $\mathbf{Set}$, а затем перейти к процессу обогащения, т. е. мы добавим в нашу теорию множеств все, что нам нужно для определения Вселенной, в которой наша теория имеет смысл. Если вам интересна эта теория, возможно, вы захотите прочитать расширенную теорию категорий и узнать о $\mathscr{V}$-обогащенных вселенных. Обратите внимание, что когда вы обогащаете свою теорию множеств, даже если у вас есть, скажем, новый способ решения проблемы остановки, теперь у вас есть $\mathscr{V}$-проблема остановки, которую вам придется снова обогатить, чтобы исправить. Эта проблема возникает бесконечно и требует какой-то трансфинитной индукции, чтобы говорить о ней точно.

Когда Аводи говорит о наборе объектов и наборе морфизмов, он имеет в виду «множество» в любой релевантной теории множеств, которая вас волнует в данный момент. Например, когда мы определяем категорию $\mathbf{Set}$, набор объектов не является набором в смысле ZFC: это правильный класс! Однако в этом случае мы просто признаем тот факт, что иногда нам нужно продвинуться вверх по вселенной теории множеств, чтобы работать. Опять упираемся в тему обогащения, что делает эту тему точной. Многие математики, в том числе и я, просто считают само собой разумеющимся, что мы живем в какой-то вселенной Гротендика и в конечном итоге должны перейти к работе с «большими» категориями. Эти категории вообще ведут себя странно, но чрезвычайно важны. Например, в алгебраической геометрии, если $X = (X,\mathcal{O}_X)$ — схема, то категория $\mathbf{\mathcal{O}_X-Mod}$ — это (в общем случае) большая абелева категория, а для любого кольца $R$ категория левых $R$-модулей с невырожденными $R$ действиями является очень хорошей абелевой категорией, al. Фактически, знаменитая теорема о вложении Митчелла-Фрейда говорит нам, что если $\mathfrak{A}$ — малая абелева категория, то существует полное и точное вложение $\mathfrak{A} \to \mathbf{R-Mod }$ для некоторого кольца единицы $R$, сохраняющего точность. Это дает нам результат, который, по сути, означает, что если вы спорите с конечной диаграммой в абелевой категории $\mathfrak{A}$, то вы также можете использовать модули и теорию модулей, чтобы облегчить себе жизнь. По большей части вы можете обращаться с объектом «Set» и морфизмом «Set» категории, как если бы они были множествами или элементами некоторой расширенной и более широкой теории, где такие вещи имеют синтаксический смысл. Только будьте осторожны: объекты в категории не обязательно должны быть множествами, и вы не можете теоретически спорить о некоторых вещах. Например, если мы имеем дело с большой абелевой категорией $\mathfrak{A}$ и у нас есть бесконечная диаграмма, с которой нам нужно иметь дело, такая как когомологически длинная точная последовательность, то мы НЕ МОЖЕМ, по крайней мере вообще, использовать Митчелл-Фрейд, и мы должны спорить об универсальных свойствах и тому подобном, за исключением особых случаев.

Отвечая на ваш третий вопрос, отметим, что разница между данными и законами заключается в том, что законы в этом смысле являются синтаксическими или алгебраическими правилами, которые ДОЛЖНЫ соблюдаться всегда, в то время как данные могут меняться. Для примера отметим, что категории $\mathbf{FinSet}$ конечных множеств и $\mathbf{FinGrp}$ конечных групп имеют разные данные: морфизмы в $\mathbf{FinSet}$ сильно отличаются от морфизмов в $\mathbf{FinGrp}$; однако морфизмы удовлетворяют тем же основным законам композиции ($f:A \to B$ и $g:B \to C$ дают композицию $g \circ f:A \to C$), тем же законам ассоциативности ($ f \circ (g \circ h) = (f \circ g) \circ h)$ и те же единичные законы ($f \circ \operatorname{id} = f, \operatorname{id} \circ f = f $)!

$\endgroup$
5
$\begingroup$

Категория состоит из чего-либо примерно так же, как группа состоит из операции и множества. Часто категория представляет собой кортеж класса объектов и класса стрелок. Однако, поскольку иногда категории имеют дело с коллекциями, которые больше, чем классы, имеет смысл использовать расплывчатый термин, который в основном означает «Используйте здесь соответствующую концепцию набора/класса/и т. д.»

$\endgroup$
9
$\begingroup$

Несколько мыслей от явно неспециалиста:

Занимаясь математикой, вы должны сначала выбрать логическую систему, в рамках которой будете работать. Практически всегда первой аксиоматической системой, знакомящейся с математиками, является ZFC, но это ни в коем случае не единственный выбор.

Теория категорий интересуется последствиями композиции событий, поэтому она определяет себя только с точки зрения того, что ей нужно:

1. У вас есть некоторые логические вещи, называемые объектами, которые вы находите интересными
2. Вещи происходят с этими объектами таким композиционным образом, что это еще $более$ интересно
3. Одна возможная вещь, которая может случиться с вашими объектами, это ничего

Тогда существует, в некотором смысле, своя теория категорий для каждого определения «логической вещи», но не все логические системы созданы равными в отношении обсуждения категориальных вопросов!

Например, у нас определенно есть логические вещи, называемые множествами, функции воздействуют на множества композиционно, а карта идентичности определенно не влияет на множество.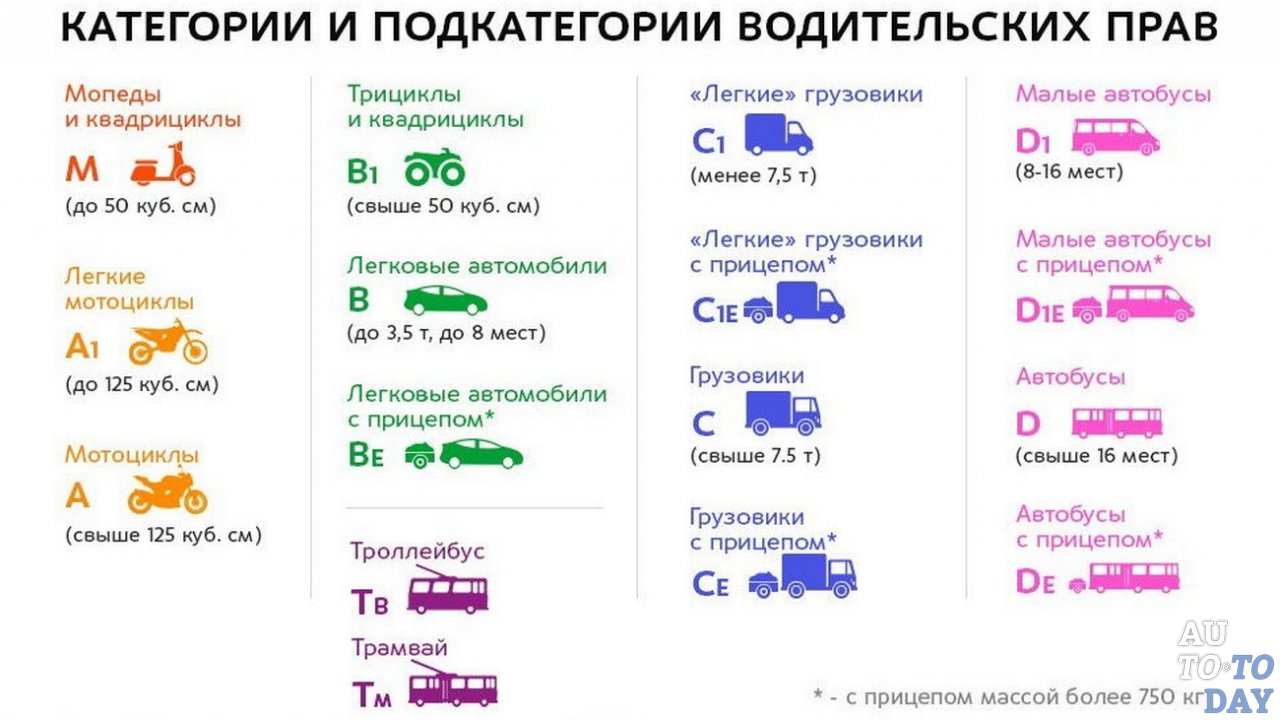 Таким образом, мы $должны$ иметь возможность говорить о категории множеств, но в ZFC делать это очень сложно, потому что, как вы уже убедились на собственном опыте, когда вы пытаетесь говорить обо всех множествах как об объектах, ZFC кричит: ваше ухо: «Это не набор, это не набор, будьте подозрительны в существовании этой штуки!»

Решение простое: если вы хотите задать категоричные вопросы о ZFC (или о теории групп, колец, модулях и многом другом), не используйте ZFC в качестве логической системы. Вместо этого вы могли бы использовать логическую систему, которая аксиоматизирует вещи, большие, чем наборы (логические вещи $a$, для которых $a\in b$ не определены), и тогда SETS (и многие другие интересные вещи!) будут в пределах вашей досягаемости. .

Примером такой системы, похожей на ZFC, является теория NBG (фон Неймана Бернайса Гёделя), в которой в качестве отправной точки используется понятие класса, но, конечно, есть и другие.

В качестве альтернативы, вы можете спросить себя, $хотите ли вы $теорию множеств при изучении теории категорий. Короче говоря, теория множеств — это аксиоматическая система, используемая для описания использования символа $\in$ таким образом, который, надеюсь, этого не делает, но, возможно, может привести к парадоксам. Поскольку теория категорий имеет тенденцию сосредотачиваться на $действиях$(которые составляют) вместо $вещей$(которые принадлежат), это редко бывает полезным. Итак, простой и, по-видимому, часто предлагаемый курс действий: возьмите то, что вы узнали из теории множеств, и просто перестаньте задавать $\in$ вопросы.

В любом случае, ваши беспокойства больше не вызывают беспокойства: SETS является разумным объектом для рассмотрения, так как вы либо используете более широкую теорию для ее изучения, либо не задаете вопросы, предполагающие отсутствие SETS.

$\endgroup$
3

теория категорий — В каких категориях моник эпи является изоморфизмом?

Существует ли общее описание категорий $\mathscr{C}$, в которых все моничные эпиграммы на самом деле являются изоморфизмами?

В общем, унитарный эпилог не обязательно должен быть изоморфизмом. 1$.

С другой стороны, в категории $R$-$\mathbf{mod}$ моника инъективна, а эпи сюръективна, а биективный морфизм является изоморфизмом; таким образом, монический эпи является изоморфизмом. По теореме Фрейда-Митчелла о вложении следует, что если $\mathscr{C}$ — малая абелева категория, то унитарный epi — изоморфизм. (См. эти вопросы, чтобы удалить условие «маленький».)

Аналогично, если $\mathscr{C}$ — конкретная категория, моничность и эпичность которой сохраняются забывающим функтором и обратным морфизмом на уровне множеств поднимается до инверсии в категории, такой как $\mathbf{Grp}$ (или $\mathbf{Set}$, если уж на то пошло), то монический + эпический изоморфизм $\Rightarrow$.

Таким образом, моник + эпик $\Rightarrow$ iso является условием, которое выполняется в абелевых категориях и некоторых других категориях, но не во всех категориях.

Существует ли разумное (например, чистое или элегантное) общее описание категорий, в которых монический + эпический $\Rightarrow$ iso?

Приложение: для тех, кто еще запутался (как и я) по поводу того, что Чжэнь Линь и Цяочу Юань упоминают ниже о хаусдорфовых и более общих топологических пространствах:

Если $X,Y$ являются топологическими пространствами и $f,g :X\rightarrow Y$ — непрерывные отображения, согласующиеся на плотном подмножестве $D\subset X$, в общем случае нет гарантии, что $f=g$.