Автошкола Фаворит Новосибирск

Добро пожаловать на сайт лучшей новосибирской автошколы! Задача инструкторов и преподавателей центра, не просто дать основные знания ПДД и навыки вождения, а сделать из каждого ученика, уверенного и спокойного на дороге водителя. Процесс обучения в автошколе построен так, чтобы знания и умения запоминались легко, без усилий. Качество преподавания заметно на экзаменах – наши курсанты показывают лучшие результаты.

Преимущества автошколы НСК

Основное направление в обучении автошколы – B-категория (на легковые ТС). Современный автодром для практики и удобные кабинеты для теории, новые комфортные автомобили и инструктора с огромным стажем – это то, что отличает нас от других. Каждый студент может подобрать автошколу рядом – несколько классов позволят быстро добираться по городу.

1. Преподаватели (теоретики и практики) с большим опытом (более 15-20 лет).	2. Несколько классов автошколы в городе.	3. Современные техники обучения.
4. Возможность оплатить обучение в автошколе в рассрочку.	5. Индивидуальный подход к ученикам.

Оптимальные цены и сроки обучения в автошколе позволят обрести прочные знание и крепкие навыки. Максимальный эффект достигается благодаря правильно выстроенной программе, опытным инструкторам. Часы для вождения в автошколе согласовываются с преподавателем, можно подобрать наиболее удобный вариант – утренние, вечерние, дневные группы. Цены на обучение в автошколе в 2020 году являются наиболее выгодными в Новосибирске.

Для студентов группы В в автошколе предоставляют современные импортные автомобили, оснащенные всем необходимым оборудованием – безопасность курсантов на первом месте. Инструкторы с многолетним опытом понимают уровень напряжения начинающего водителя, поэтому максимально мягко позволяют осваивать маневры и всегда помогут практическим советом. Автодромы оборудованы в соответствии с европейскими стандартами и оснащены всем необходимым для выполнения учебных элементов.

Хочу в автошколу – где я могу учиться?

Несколько классов автошколы расположены на правом берегу, еще несколько кабинетов автошколы – на левом берегу. В первую очередь это удобно для студентов – выбрать можно любой удобный класс и обучаться рядом с домом. Таким образом можно быстро добраться до автошколы и получить максимальную пользу от занятий.

Цена и сроки в автошколе

Обучение проводится по строгому регламенту и в соответствии с требованиями ГИБДД. Оплату за автошколу можно внести разными способами – наличными в офисе, безналичными (например, банковским переводом или картой). Для каждого студента предусмотрена возможность внесения платежей за автошколу в рассрочку – равными частями и без дополнительных процентов, комиссий.

Срок обучения зависит от категории. Например, для курсантов, обучающихся на права «В» предусмотрено минимум 3 месяца. За этот период студенты нашей автошколы (правого берега и левого) получают необходимые знания и навыки в полном объеме. После выпуска наши ученики чувствуют себя на дороге спокойно и уверенно.
Наша автошкола одной из первых получила лицензию на обучение и соответствует новым строгим стандартам и требованиям. Студенты сдают экзамены уверенно, а затем пополняют число профессиональных водителей. Чтобы узнать подробности и даты начала обучения, а также как записаться в группу, достаточно позвонить по телефону или обратиться напрямую в офис. Лучшая новосибирская автошкола ждет Вас!

Автошкола Всероссийского Общества Автомобилистов г.Чебоксары

Мотоциклы

Категория А

Водительское удостоверение категории А позволяет управлять любыми мотоциклами, в том числе и мотоциклами с коляской. Кроме того, водительское удостоверение категории A позволяет управлять и мотоколясками, которые в настоящее время на дорогах встретить чрезвычайно сложно.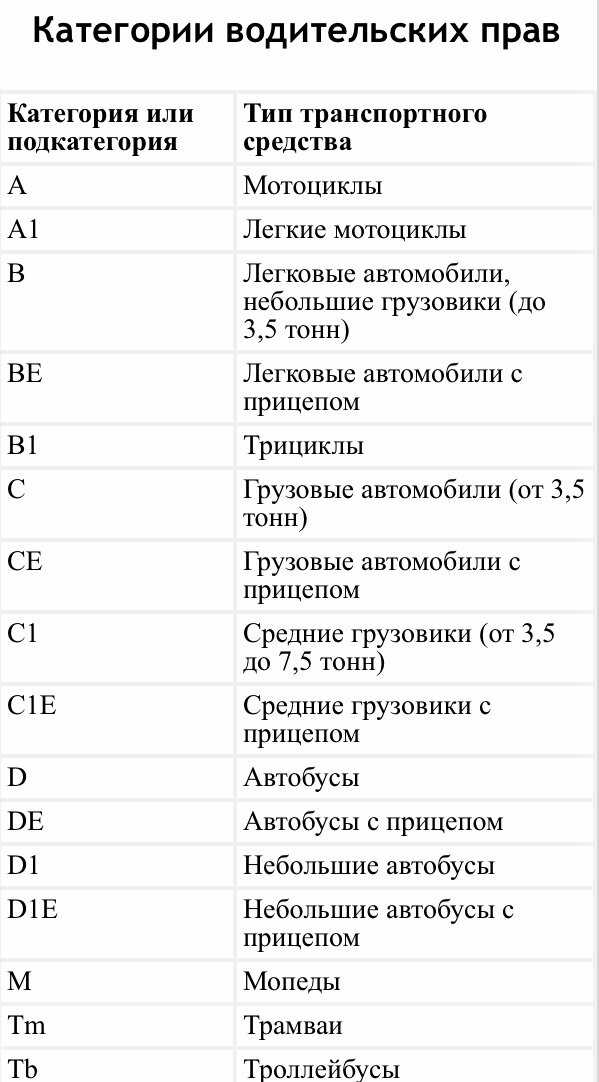

Подкатегория А1

Подкатегория «А1» — мотоциклы с рабочим объемом двигателя внутреннего сгорания, не превышающим 125 кубических сантиметров, и максимальной мощностью, не превышающей 11 киловатт;

Подкатегория А1 позволяет управлять мотоциклами с небольшим объемом двигатели и небольшой максимальной мощностью.

Стоит отметить, что водители, имеющие в правах категорию А могут управлять и транспортными средствами подкатегории А1.

Автомобили, Трициклы и Квадрациклы

Категория B — автомобили

Категория «В» — автомобили (за исключением транспортных средств категории «А»), разрешенная максимальная масса которых не превышает 3500 килограммов и число сидячих мест которых, помимо сиденья водителя, не превышает восьми.

Водительское удостоверение категории В позволяет управлять легковыми автомобилями, а также небольшими грузовиками, микроавтобусами и джипами, соответствующими вышеприведенным требованиям. Также категория B позволяет управлять мотоколясками и автомобилями с прицепом (разрешенная максимальная масса которого не более 750 кг).

Подкатегория B1 — трициклы и квадроциклы

Категория «В1» водительских прав предоставляет возможность управлять трех- или четырехколесным автомобилем, порожняя масса которого не превышает 550 кг. Его изготовительская скорость превышает 50 км/ч. В случае, если транспорт имеет двигатель внутреннего сгорания, то его рабочий объем будет более 50 куб.см.

Автомобили

Категория C

Категория «С» — автомобили, за исключением автомобилей категории «D», разрешенная максимальная масса которых превышает 3500 килограммов; автомобили категории «С», сцепленные с прицепом, разрешенная максимальная масса которого не превышает 750 килограммов;

Подкатегория C1

Подкатегория «С1» — автомобили, за исключением автомобилей категории «D», разрешенная максимальная масса которых превышает 3500 килограммов, но не превышает 7500 килограммов; автомобили подкатегории «С1», сцепленные с прицепом, разрешенная максимальная масса которого не превышает 750 килограммов;

Автомобили

Категория D

Водительское удостоверение категории Д позволяет управлять автобусами различных размеров, не зависимо от их разрешенной максимальной массы, а также автобусами с прицепом, разрешенная максимальная масса которого не превышает 750 кг. Для более тяжелых прицепов также требуется водительское удостоверение категории DE.

Подкатегория D1

Подкатегория D1 позволяет водителю управлять маленькими автобусами, имеющими от 9 до 16 сидячих мест. Также эта категория разрешает использовать легкий прицеп массой до 750 кг.

Мопеды и легкие квадроциклы

Категория M

Новая категория М, введенная 5 ноября 2013 года, позволяет управлять мопедами и легкими квадроциклами.

Управлять транспортными средствами категории М также могут и водители, у которых нет категории М, но есть любая другая категория водительских прав.

Ab-категорий « Непримиримый математик

Математика для интересующихся со стороны

Ab-Категории

Теперь, когда мы в абстракции многое сделали с обогащенными категориями, давайте рассмотрим очень полезный частный случай категорий, обогащенных свыше, — категорию абелевых групп.

Мы знаем, что это моноидальная категория с тензорным произведением абелевых групп в качестве ее моноидальной структуры и свободной абелевой группой в качестве моноидальной единицы. Еще лучше, чтобы он был симметричным и даже закрытым. То есть для любых двух абелевых групп и у нас есть изоморфизм , и существует естественная структура абелевой группы на множестве гомоморфизмов, удовлетворяющих присоединению .

Далее, является полным и сополным. Все вместе это означает, что это отличный кандидат в качестве базовой категории для создания расширенных категорий. Конечно, они будут называться -категориями.

Итак, давайте прочитаем определения. -категория имеет набор объектов, а между объектами и есть абелева хом-группа.

Для каждого объекта у нас есть гомоморфизм абелевых групп, который выделяет «тождественный морфизм» из в себя на уровне лежащих в его основе множеств. Помните, что мы больше не думаем об абелевой группе как о наличии элементов — только ее базовый набор больше содержит элементы, а базовый набор абелевой группы — это 9 элементов.0017 множество гомоморфизмов абелевых групп.

Для трех объектов у нас есть стрелка «композиция» в : . Это ассоциативно, и тождественный морфизм действует как тождество в том смысле, что соответствующие диаграммы коммутируют. Конечно, поскольку стрелки композиции являются морфизмами, они являются линейными функциями на каждом входе.

-функтор между -категориями и определяется функцией от объектов к объектам и для каждой пары объектов гомоморфизмом абелевых групп . Для коммутации требуются две диаграммы, говорящие о том, что эти линейные функции сохраняют функции композиции и идентичности.

Естественная трансформация — одна из двух форм. В одном нам дано два -функтора и . Тогда натурал — это набор линейных функций, коммутирующих одну диаграмму. В другом нам дан объект и бифунктор. Тогда это набор линейных функций, коммутирующих другую диаграмму.

Вместе -категории, -функторы между ними и -естественные преобразования (первого рода) образуют 2-категорию. Мы можем соединить вне-категории и получить категорию продукта (на самом деле мы уже сделали однажды выше), и мы можем взять противоположную категорию. Таким образом, -категории образуют симметричную моноидальную 2-категорию с инволюцией двойственности.

Здесь очень много структур, но в конечном итоге все сводится к тому, что «все хом-множества имеют структуру абелевых групп, и все в поле зрения является -линейным». И это обычное определение, от которого я решил отказаться, когда начал работать с расширенными категориями.

Нравится:

Нравится Загрузка…

14 сентября 2007 г. — Автор: Джон Армстронг | Теория категорий

« Предыдущая | Следующий »

• Последние сообщения

  • Подмодуль инвариантов
  • Больше новых модулей из старых
  • Новые модули из старых
  • Приводимые модули
  • Неприводимые модули
  • Модули Алгебры Ли
  • Все выводы полупростых алгебр Ли являются внутренними
  • Разложение полупростых алгебр Ли
  • Назад к примеру
  • Радикал убийственной формы
  • Форма убийства
  • Критерий Картана
  • Следовый критерий нильпотенции
  • Использование разложения Жордана-Шевалле
  • Разложение Жордана-Шевалле (доказательство)

• Блогролл

• Арт.

  
  • Эскизы топологии

• Астрономия

  • Плохая астрономия
  • Начинается на ура

• Информатика

  • Хорошая математика, плохая математика
  • Местечко-Оптимизированный
  • Вселенная дискурса

• Образование

  • Меловая пыль заставляет меня чихать
  • Непрерывность
  • ф(т)
  • На полпути
  • Математическое безумие Мэриленда
  • Математика Будь храбрым
  • Математика под микроскопом
  • Mathspig
  • Очень трудные суммы
  • Стивен Строгац
  • Музей математики
  • Призрачный профессор
  • Почему мальчики терпят неудачу

• Математика

  • Диалог о бесконечности
  • Сингулярная непрерывность
  • Арс Математика
  • Картер и сложность
  • Любопытные рассуждения
  • Борьба с сопротивлением материи
  • Бог играет в кости
  • Хорошая математика, плохая математика
  • Блог Гауэрса
  • Гире&Гимбл
  • Внутренний узел
  • Низкоразмерная топология
  • Математика и физика
  • Математика под микроскопом
  • Блог Мичи
  • Очень трудные суммы
  • Строгие мелочи
  • Секретный семинар по ведению блога
  • Эскизы топологии
  • Стивен Строгац
  • Сумидиот
  • Семинар «Все»
  • Музей математики
  • Кафе n-категории
  • Вселенная дискурса
  • Теоретический атлас
  • Находки этой недели по математической физике
  • Топологические размышления
  • Что нового

• Я

  • DrMathochist
  • Непримиримый программист

• Философия

  • Диалог о бесконечности
  • Узлы «если-то»
  • Плектикс
  • Кафе n-категории

• Физика

  • Гравитация и Левитация
  • Воображаемый потенциал
  • Даже не ошибся
  • Разглагольствования разгневанного физика
  • Наука после Sunclipse
  • Начинается на ура
  • Язык плохой физики
  • Кафе n-категории

• Политика

  • Плохая астрономия
  • На полпути
  • Почему мальчики терпят неудачу

• Наука

  • Плохая астрономия
  • Плектикс
  • Наука4Взрослые

• Обратная связь

  Есть что сказать? Анонимные вопросы, комментарии и предложения на Formspring. me!

• Субъекты

  Субъекты категория категория (550) Теория категории (152) Универсальные свойства (7) Теория группы (114) Абелевские группы (4) Групповые действия (9) Групповые примеры (6) Групповые гомоморфизмы (5) Структура групп (10) Подгруппы и группы коактирования (2) Решетки (5) Алгебры Ли (31) Группы Ли (4) Линейная алгебра (155) Квандели (2) Теория представлений (146) Представления симметричных групп (56) Теория колец (62) Степенные ряды (8) Полиномиальные ряды 13)      Структура колец  (2)Анализ  (293) Вариационное исчисление (1) Дифференциальные уравнения (13) Функциональный анализ (12) Теория меры (126) Комбинаторика (2) Основы (30) Числа (19) Порядки (9) Геометрия (66) Алгебраика 1) Аналитическая геометрия (5) Дифференциальная геометрия (18) Системы корней (38) Теория узлов (23) Математическая физика (32) Электромагнетизм (28) Ранты (16) Специальные темы (31) Атлас групп Ли (14) Бильярд (4) )   Криптография  (1)   Механизм Хиггса  (4)   Кубик Рубика  (8)Топология  (172)   Дифференциальная топология  (128)   Топология с множеством точек  (31)Без категорий (121)

• Архив

• Поиск:

абстрактная алгебра — Копроизведения в $\text{Ab}$

Задай вопрос

спросил 10 лет, 1 месяц назад

Изменено 1 год, 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Сейчас я пытаюсь понять, почему конечные произведения и копроизведения в категории $\text{Ab}$ совпадают. На самом деле, я даже не уверен, что смогу это показать. Мой вопрос следующий:

Есть ли интуитивно понятный способ понять, почему конечные произведения и копроизведения в $\text{Ab}$ совпадают, а в $\text{Grp} — нет?$

Что касается формального направления, я не уверен, показал ли я, что они совпадают. Идея состоит в том, чтобы показать, что $G\times H$ удовлетворяет универсальному свойству копроизведений для $G,H \in \text{Obj}(\text{Ab})$.

Попытка

Я определил функции включения $\iota_G:G\longrightarrow G\times H$ и $\iota_H:H\longrightarrow G\times H$ с помощью $\iota_G(g)=(g,1_G) $ и $\iota_H(h)=(1_H,h)$. Предположим, что $\varphi:G\longrightarrow K$ и $\psi:H\longrightarrow K$ являются гомоморфизмами. Чтобы показать, что $G\times H$ является копроизведением в $\text{Ab}$, мне нужно построить уникальную функцию $\tau:G\times H\longrightarrow K$ такую, что $\varphi=\tau\circ \iota_G$ и $\psi=\tau\circ\iota_H$. Таким образом, я определил $\tau$ как $\tau(g,1_H)=\varphi(g)$ и $\tau(1_G,h)=\psi(h)$. Я думаю, что это должно работать, поскольку для всех $(g,h) \in G\times H$ мы имеем $(g,h)=(g,1_H)*(h,1_H)$, поэтому, определив $\tau$ так что $\tau(g,h)=\tau(g,1_H)*\tau(h,1_H)$ все должно работать.

• абстрактная алгебра
• теория групп
• теория категорий
• абелевы группы

$\endgroup$

5

$\begingroup$

Категория $\mathsf{Ab}$ абелевых групп и их гомоморфизмов является примером предаддитивной категории. В предаддитивной категории понятия (конечного) продукта и копроизведения совпадают, т.е. $$A \times B \cong A + B \cong A \oplus B$$ где $\oplus$ обозначает побочное произведение $A$ и $B$.

В произвольной категории побочное произведение определяется следующим образом: $X$ является побочным произведением $A$ и $B$, если существуют отображения $$A \overset{\pi_A}{\underset{\iota_A}{\leftrightarrows}} X \overset{\pi_B}{\underset{\iota_B}{\rightleftarrows}} B$$ превращение $(A \overset{\pi_A}{\leftarrow} X \overset{\pi_B}{\rightarrow} B)$ в произведение и $(A \overset{\iota_A}{\rightarrow} X \overset{\ iota_B}{\leftarrow} B)$ в копроизведение.

Теперь предаддитивные категории имеют аддитивную структуру на своих хомсетах. Например, в $\mathsf{Ab}$, если $f, g : A \rightrightarrows B$ являются гомоморфизмами между абелевыми группами $(A,+)$ и $(B,+)$, то мы можем получить другой гомоморфизм $ f+g : A \to B$ определяется как $$(ж+г)(а)=е(а)+г(а)$$ Тогда бинарная операция $+$ дает $\text{Hom}_{\mathsf{Ab}}(A,B)$ абелеву групповую структуру. Элементом единицы является отображение нулей $0 : A\to B$, которое есть нулевой морфизм в теоретико-категориальном смысле.

Существует результат, который утверждает, что $(A \overset{\pi_A}{\underset{\iota_A}{\leftrightarrows}} X \overset{\pi_B}{\underset{\iota_B}{\rightleftarrows}} B )$ является побочным произведением тогда и только тогда, когда выполняются все следующие условия:

• $\pi_A \circ \iota_A = \text{id}_A$ и $\pi_B \circ \iota_B = \text{id}_B$
• $\pi_B \circ \iota_A = 0 : A \to B$ и $\pi_A \circ \iota_B = 0 : B \to A$
• $\iota_A \circ \pi_A + \iota_B \circ \pi_B = \text{id}_X$

Это намекает на то, почему это работает в $\mathsf{Ab}$, но не в $\mathsf{Grp}$: в $\mathsf{Grp}$ у нас нет аддитивной структуры на хомсетах, таких как $\mathsf{Ab }$ делает. [И действительно, копроизведение двух групп в $\mathsf{Grp}$ является свободным произведением; в $\mathsf{Ab}$ это прямое произведение суммы $\equiv$ декартово.]

Стоит попытаться доказать приведенный выше результат и проработать его на (более) конкретном примере.

---

П.С. Спасибо Александр Тумм за напоминание о предаддитивных категориях.

Изменить: см. комментарии.

$\endgroup$

7

$\begingroup$

Пусть $\mathcal A = \text{AbGrp}$. Позже будет важно, что $\mathcal A$ имеет нулевой объект $0$ и нулевые морфизмы.

Ключевое свойство состоит в том, что каждое хом-множество $\mathcal A(A,B)$ является абгруппой. Пусть $f_1, f_2 : A \longrightarrow B$, затем определим $f_1 + f_2 : A \longrightarrow B$ просто как $(f_1 + f_2)(a) = f_1(a) + f_2(a)$, легко увидеть это групповой гомоморфизм. Более того, в $\mathcal A$ композиция распределяется: Имеются тождества $g(f_1+f_2) = gf_1 + gf_2$ и $(g_1+g_2)f = g_1f + g_2f$.

Этого не происходит в $\mathcal G = \text{Grp}$ Предположим, что мы положили $(f_1 \star f_2)(a) = f_1(a) \star f_2(a)$, тогда $v$ не не является групповым гомоморфизмом, поскольку $(f_1 \star f_2)(a \cdot b) = f_1(a) \star f_1(b) \star f_2(a) \star f_2(b)$, вообще говоря, не равно $ (f_1 \star f_2)(a) \star (f_1 \star f_2)(b) = f_1(a) \star f_2(a) \star f_1(b) \star f_2(b)$.

---

Теперь позвольте мне представить побочный продукт $A \oplus B$, который является объектом с картами

• $\pi_1 : A \oplus B \longrightarrow A$
• $\pi_2 : A \oplus B \longrightarrow B$
• $\iota_1 : A \longrightarrow A \oplus B$
• $\iota_2 : B \longrightarrow A \oplus B$

удовлетворяющие тождествам

• $\pi_1 \iota_1 = 1_A$
• $\pi_2 \iota_2 = 1_B$
• $\pi_2 \iota_1 = 0$
• $\pi_1 \iota_2 = 0$
• $\iota_1 \pi_1 + \iota_2 \pi_2 = 1_C$

обратите внимание, что это определение самодвойственно.

---

Лемма $C$ является произведением $A$ и $B$ тогда и только тогда, когда оно является* побочным произведением $A$ и $B$. (мы не показываем уникальные побочные продукты, но они есть).

эскиз доказательства : ($\Rightarrow$) Вы можете построить $\iota_1, \iota_2$, используя уравнения, и вы можете доказать последнее тождество, показав сначала $\pi_1 (\iota_1 \pi_1 + \iota_2 \pi_2) = pi_1$, тогда $\pi_2 (\iota_1 \pi_1 + \iota_2 \pi_2) = pi_2$ . ($\Leftarrow$) Нужно только показать, что бипроизведение обладает универсальным свойством произведений (единственностью универсального отображения).

Следствие (по двойственности) $C$ является копроизведением $A$ и $B$ тогда и только тогда, когда оно является* побочным произведением $A$ и $B$.

Следствие Произведения и Копроизведения совпадают.

---

Свойства $\mathcal A$, которые мы использовали, называются предаддитивной категорией , но я попытался сделать это как можно более элементарным, поэтому просто обратите внимание, что $\mathcal A$ — это один пример, а $\mathcal G$ — нет.

Мы еще не видели, почему произведения и копроизведения в $\mathcal G$ не совпадают…

$\endgroup$

1

$\begingroup$

Как указывает Томас Эндрюс, было бы полезно рассмотреть произведения и копроизведения возможно бесконечных наборов абелевых групп. Попытайтесь понять следующие два факта:

1) Произведения и копроизведения абелевых групп соответствуют прямым произведениям и прямым суммам соответственно.

2) Для конечных наборов абелевых групп прямое произведение и прямая сумма оказываются канонически изоморфными.

$\endgroup$

$\begingroup$

Имея немного больше информации и опыта, я подумал, что, возможно, мне следует добавить это размышление в качестве ответа для всех, кто воспользуется этим вопросом в будущем.