Момент силы • 7 класс • Физика

Содержание

Момент силы зависит от длины плеча. Для многих подобная фраза — просто сухой набор фактов. На самом деле, если разобраться, за терминами «длина плеча», «момент силы» прячутся удобные и вполне понятные физические концепции. На данном уроке мы приподнимем над всем этим завесу тайны, а также откроем для себя условие равновесия и правило моментов. Нюансы а-ля в чем там измеряется момент силы и формула момента силы прилагаются!

Момент силы: вновь Архимед и его рычаг

Поговаривают, что древнейшим открытием и в какой-то степени самым первым научным достижением человека можно смело называть рычаг. Удивительно, но наши предки на уровне интуиции понимали, что увесистый камень намного проще поднять или передвинуть с помощью самой обычной палки. При этом удивляет больше не наличие палки во всей этой истории, а осознание первобытным человеком принципа простых механизмов. Ведь палки первые разумные жители планеты специально искали подлиннее. Они понимали: чем длиннее, тем будет проще совершить работу.

«Катить проще, чем тянуть» — еще одно древнейшее «научное»  открытие примитивного человека наряду с рычагом.

Принцип рычага передавался из уст в уста, от одного племени к другому, от одного поколения к следующему. Мы не знали, почему это работает. У нас не было формул, не было определений. Был лишь рычаг в самых его разных формах проявления и четкое знание — возьмись подальше от точки опоры, если тяжело.

И лишь в третьем веке до нашей эры Архимед впервые произвел необходимые математические расчеты. Он наконец описал теорию рычага, которой мы пользуемся и по сей день. Он первым связал друг с другом понятия груза, плеча и силы. Как гласит легенда, осознав масштабы своего открытия, воскликнул: «Дайте мне точку опоры, и я переверну Землю!»

Благодаря опытам Архимеда, его фундаментальному пониманию закона равновесия рычага, впоследствии возникла крайне важная физическая величина — момент силы.  

Закон равновесия: опыт с грузами

Определить момент силы можно разными способами. Мы воспользуемся самым простым. Нам достаточно вспомнить условие равновесия рычага и провести несложный опыт с подвешенными грузами. 

Во-первых, возьмем небольшую деревянную балку. К ее верхнему концу прикрепим болтом мерную линейку таким образом, чтобы крепление располагалось в центре тяжести линейки (рисунок 1). Далее к линейке прикрепим по сантиметровым делениям два крючка, за которые будем подвешивать грузики разной массы. Начнем с отметок $10 \space см$ и $20 \space см$ — по пять влево и вправо от центра тяжести в $15 \space см$. 

Рисунок 1. Простая система из линейки, балки, крепления и крючков

Возьмем грузик массой $20 \space г$ и подвесим его за крючок (рисунок 2). Очевидно, что рычаг в результате не окажется в положении равновесия. 

Рисунок 2. Справа от точки опоры рычага подвешиваем первый грузик массой $20 \space г$

Теперь с другой стороны от центра тяжести подвесим грузик массой $40 \space г$ (рисунок 3). Очевидно, что рычаг снова не окажется в положении равновесия: с левой стороны на плечо рычага действует бó‎льшая сила $mg$. 

Рисунок 3. Отклонение рычага в левую сторону при подвешивании второго грузика массой $40 \space г$

Приводим рычаг в равновесие

Интуитивно мы понимаем, что дабы соблюсти условие равновесия данной системы, один из грузиков нужно куда-то сместить. Мы так же интуитивно понимаем, что если смещать грузик массой $40 \space г$, его нужно подвесить за крючок, располагающийся ближе к точке опоры. Смещать грузик массой $20 \space г$ нужно в другую сторону — подальше от точки опоры.

Вопрос на миллион: если, скажем, мы хотим перевесить двадцатиграммовый грузик, на сколько делений должно увеличиться плечо груза?

Используем стандартный метод проб и ошибок. Перевешивая крючок с грузиком по разным отметкам на линейке, мы обнаружим, что рычаг придет в положение равновесия, если двадцатиграммовый грузик подвесить на расстоянии десяти сантиметров от точки опоры — на отметке $25 \space см$ (рисунок 4). Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40 \space г$ и $20 \space г$ уравновешивают друг друга на плечах длиной $5 \space см$ и $10 \space см$ соответственно. 

Рисунок 4. Рычаг в положении равновесия

Условие равновесия

Именно таким образом Архимедом было сформулировано условие равновесия рычага. Можно долго перевешивать грузики, пользоваться различными массами, рычагами короткими, рычагами длинными, но одна вещь всегда будет объединять все элементы и переменные:

Рычаг находится в положении равновесия при условии, что отношение масс, подвешенных грузов, будет обратно пропорционально отношению расстояний от точки опоры до центров тяжести грузов:
$\frac{m_1}{m_2}=\frac{l_2}{l_1}$.

Если от масс перейти к силам, формулу можно улучшить до следующего вида:
$\frac{m_1g}{m_2g} = \frac{l_2}{l_1}$.

Лучше, но все равно не то. Где гарантии, что на наш абстрактный грузик будет действовать только сила тяжести? Ведь на грузик можно и надавить. Так что улучшим пропорцию еще раз и придем к окончательному

математическому выражению под условие равновесия:
$\frac{F_1}{F_2} = \frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, действующие на рычаг, $l_1$ и $l_2$ — плечи сил.

Таким образом: 

Рычаг находится в положении равновесия, когда отношение сил, действующих на рычаг, обратно пропорционально отношению плеч этих сил.  

А теперь заметим, что согласно основному свойству пропорции из формулы выше получается следующее равенство:
$F_1\cdot l_1 = F_2\cdot l_2$.

Ранее мы с подобным не сталкивались — с произведением силы на плечо силы. Именно это произведение и называется в физике момент силы.

Определение момента силы

Момент силы — физическая величина, характеризующая действие силы. Равняется произведению модуля силы на ее плечо.

Формула момента силы соответственно следующая:

$M = F \cdot l$,

где $F$ — модуль силы, $l$ — длина плеча.

Обратите внимание на то, как выглядит формула момента силы: в физике момент силы обозначается заглавной латинской литерой $M$ и измеряется в $Н \cdot м$ — в ньютонах на метр. Характеризует момент силы, как мы указали в определении, действие силы.

Так-так, в чем измеряется момент силы?

Еще раз, формула момента силы включает в себя произведение модуля силы на длину плеча. Сила $F$ измеряется в ньютонах. Длина плеча, как и любая другая длина, согласно СИ измеряется в метрах. Ну и в чем же тогда измеряется момент силы? В ньютонах на метр ($H\cdot м$), разумеется.

И как понять, что характеризует момент силы?

Возьмем гаечный ключ. Ухватимся рукой за его конец и приложим некоторое усилие, чтобы провернуть гайку. После перехватим гаечный ключ примерно до середины ручки и также попробуем приложить некоторое усилие. Во втором случае провернуть гайку будет сложнее, чем если бы мы держались за конец ручки инструмента.

Рисунок 5. Опыт с гаечным ключом. Обратите внимание на направление момента силы $M$

Причина? Образуются разные величины момента силы! Помните, как мы говорили о механическом выигрыше на прошлом уроке? При нем образуется бóльший момент силы.

Иными словами, момент силы — это и есть в своем роде величина усилия. Чем больше момент, тем быстрее двигается предмет, тем проще он проворачивается, тем легче выполняется действие. Формула момента силы наглядно это демонстрирует.

Как рассчитать момент силы

Момент силы всегда рассчитывается как произведение модуля силы на плечо силы:
$M = F \cdot l$.

Иногда определять приходится результирующий момент — когда на тело действует несколько разнонаправленных сил. Однако подобные «превратности» нам встретятся в программе лишь через пару лет.

Момент силы трапеции

Для примера возьмем нечто отвлеченное от привычных нам двуплечих рычагов — ясно, что внутри подобной механической системы плечо силы чаще всего будет совпадать с плечом рычага, так что сложности как таковой с расчетом плеча силы не возникнет. Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!.. 

Итак, наша вращающаяся трапеция. Силу мы прикладываем к концу фигуры — направление силы указано на изображении (рисунок 6). Согласитесь, увидеть плечо силы для подобной схемы движения уже не так просто, особенно когда глаз привык к рычагам.

Рисунок 6. Приложение силы к трапеции

Не паникуем и вспоминаем, что плечо силы есть перпендикуляр к линии действия силы, опущенный из точки опоры или, вернее сказать, из оси вращения (рисунок 7).

Рисунок 7. Плечо силы трапеции

Плечо силы будет равно длине отрезка $OA$. Ось вращения трапеции находится в точке $О$. Все гениальное просто, согласны?

Знак момента силы

Еще один немаловажный момент при расчете момента силы — знак величины. Момент может быть отрицательным или положительным. Это зависит от того, в каком направлении действует сила, приложенная к телу. Если она вращает тело по часовой стрелке, то момент силы считается положительным. Если наоборот — против часовой стрелки, то момент считается отрицательным. 

Рисунок 8. Знак момента силы

Может ли момент быть нулевым? Конечно, почему нет. Логично предположить, что в случае, если плечо силы равно нулю, то сила не создает никакого момента. Например, если вы надавите на ось вращения, сдвинуть при таком приложении силы что-либо невозможно.

Задача на моменты

Образавр предлагает решить задачу самостоятельно!

На земле лежит палка массой $20 \space кг$ и длиной $4 \space м$. Палку приподнимают за конец, прикладывая усилие в $120 \space Н$. Какие моменты при этом создают силы, действующие на доску? Моменты силы тяжести в поднятом положении палки и в вертикальном положении к земле равны.

Дано:
$m = 20 \space кг$
$d = 4 \space м$
$F = 120 \space Н$

$M — ?$

Рисунок 9. Схема рычага к задаче

Решение задачи на моменты

Показать решение и ответ

Скрыть

На палку действуют: сила реакции опоры $\vec{N}$, сила тяжести $m\vec{g}$ и внешняя сила, которую мы прикладываем к концу, $\vec{F}$. Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.

Плечо силы реакции опоры $\vec{N}$ равно нулю: точка приложения силы и ось вращения совпадают. Следовательно $M_N$ силы реакции опоры мы можем определить сразу. Он равен нулю:
$M_N = 0$.

Далее опускаем перпендикуляр из оси вращения $B$ к внешней силе $\vec{F}$. Получаем, что плечо внешней силы $\vec{F}$ равно длине палки $d$:
$l_F = d$.

По формуле $M = F \cdot l$, зная, что по условию задачи длина палки составляет $4 \space м$, а модуль внешней силы равен $120 \space Н$, рассчитаем момент внешней силы $M_F$. Вращение происходит по часовой стрелке, следовательно, момент будет положительным по знаку.

Считаем:
$M_F = 120 \cdot 4 = 480 \space H \cdot м$.

Нюанс и финальный расчет

Если допустить, что момент силы тяжести $M_{mg}$ в поднятом положении палки равен моменту в вертикальном положении к земле, то плечо силы тяжести $l_{mg}$ равно половине длины палки:
$l_{mg} = \frac{1}{2} \cdot d =2 \space м$.

Примечание. Подобное допущение необходимо исключительно для простоты расчетов. Если бы пришлось определять плечо силы тяжести «честно», в задаче также должны фигурировать как минимум высота подъема палки и угол подъема.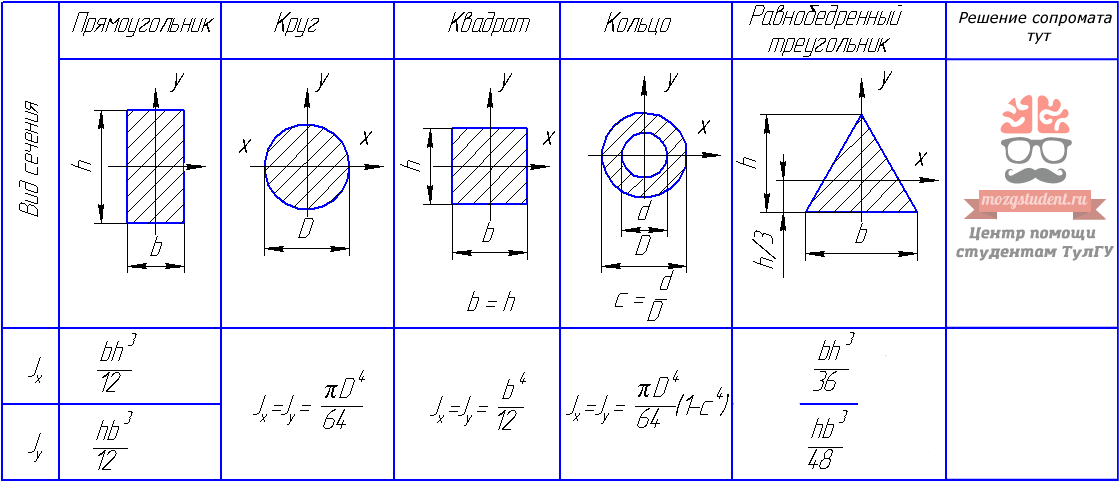 Для вычисления плеча в треугольнике понадобились бы теорема косинусов и признаки подобия треугольников. Такие дела… Поэтому считаем «нечестно». Нахождением сложных плеч вы будете заниматься в курсе статики для 10 класса.

Теперь рассчитаем момент силы тяжести $M_{mg}$ по формуле моментов, учитывая, что движение происходит против часовой стрелки. Момент отрицательный:

$M_{mg}=-\frac{1}{2}\cdot mg\cdot l_{mg}=-0.5 \cdot 20 \cdot 9.8 \cdot 2 =-196~Н \cdot м$.

Ответ: $M_N = 0$, $M_F = 480 \space Н\cdot м$, $M_{mg} = -196 \cdot Н \cdot м$.

Правило моментов

Остается последнее — разобраться, зачем нужно отрицательное значение момента силы.

Ранее мы говорили о том, что условие равновесия рычага — обратная пропорциональность отношений сил к плечам этих сил. Однако условие равновесия можно задать и через смежное понятие момента силы. В некоторых случаях даже удобнее для вычислений. 

Рисунок 10. Трапеции в состоянии равновесия

Вернемся к нашей вращающейся трапеции. Представим, что вы стоите и прикладываете к одному концу трапеции силу $\vec{F}_1$. Ваш друг берется за другой конец трапеции и тянет фигурку в противоположную сторону c силой $\vec{F}_2$. Вы в одну сторону, он в другую. При этом трапеция вращаться никуда не хочет. Она упрямо находится в положении равновесия. Но, казалось бы, моменты сил создаются. Где движение?

Правило моментов — формула

Дело в том, что один момент силы, условно говоря, «гасит» другой. Математически вычитается. Как только создаваемый вами момент силы превысит тот, что создается вашим другом, фигурка начнет движение по часовой стрелке, к вам. Если друг поднажмет, то трапеция пойдет против часовой стрелки, от вас.

Таким образом, мы можем складывать все моменты, действующие на тело, чтобы понимать, движется ли тело, и если да, то в какую сторону. Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке. Если отрицательна — против часовой.

А если сумма моментов равна нулю?

Логично, что тогда тело находится в положении равновесия. Оно не двигается. Вот как мы можем получить условие равновесия (неважно — рычага или другого тела), выраженное через момент силы.

Подобное равенство называется правило моментов.

Тело находится в состоянии покоя, если алгебраическая сумма всех моментов сил, приложенных к телу, равняется нулю:
$\sum_i M_i= M_1+M_2+…+M_i =0$. 

{"questions":[{"content":"Момент силы рассчитывается по формуле[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$M = \\frac{F}{l}$","$M = Fl$","$M = \\frac{F_1l_1}{F_2l_2}$","$M = Al$"],"answer":[1]}},"hints":[]}]}

Как рассчитать крутящий момент по оборотам в минуту: исчерпывающая информация —

В этом посте будут представлены различные методы расчета крутящего момента по оборотам и их подробное описание.

Крутящий момент — это форма силы, которая всегда измеряется в круговом движении. Напротив, RPM можно расширить, поскольку обороты в минуту используются для расчета оборотов тела, движущегося по кругу, с учетом ограничения по времени. Его можно использовать для измерения величины крутящего момента.

Давайте сначала поймем краткое значение крутящего момента и оборотов в минуту.

Крутящий момент

При круговом движении наблюдаемая сила обычно представляет собой крутящий момент.

Крутящий момент — это круговая сила, которая обычно наблюдается при круговом движении. Такого рода сила всегда наблюдается в шестернях двигателя. Итак, крутящий момент — это стихийная сила, наблюдаемая в повседневной жизни.

Изучить значение RPM или оборотов в минуту.

Что вы имеете в виду под РПМ?

Аббревиатура RPM может быть расширена до числа оборотов в минуту.

Чтобы ясно понять число оборотов в минуту, мы должны рассчитать число оборотов любого материала или объекта при круговом движении по своей орбите за определенное время. Он отличается от крутящего момента с точки зрения нагрузки на объект.

Чтобы проверить, как рассчитать крутящий момент из оборотов в минуту и ​​использовать мощность в лошадиных силах.

Изображение кредита: Бесплатные изображения Pixabay
Как рассчитать крутящий момент из оборотов в минуту и ​​л.с.?

Основными методами измерения крутящего момента являются использование RPM, то есть оборотов в минуту, и HP, лошадиных сил.

• Первый метод

               Крутящий момент = 63025 x мощность (измеряется в л.с.) / скорость (измеряется в об/мин)

• Второй метод

               Мощность (измеряется в л.с.) = крутящий момент x скорость (измеряется в об/мин) / 63025

• Третий метод

Крутящий момент (измеряется в Нм) = 9.5488 x мощность (в лошадиных силах) / скорость (измеряется в об/мин)

• Четвертый метод

              Мощность (измеряется в лошадиных силах) = крутящий момент (измеряется в Нм) / 9. 5488

Это различные методы измерения крутящего момента с использованием RPM и HP.

Как рассчитать крутящий момент по оборотам и весу?

Можно определить простую формулу для расчета крутящего момента с использованием оборотов в минуту и ​​веса/нагрузки ниже,

Чтобы сначала измерить величину крутящего момента, действующего на вес, мы должны умножить крутящий момент и смещение рычага от оси вращения, что называется радиусом круглого шкива.
Например, если масса объекта должна составлять 25 ньютонов, а расстояние от оси вращения до груза равно 7 см, то необходимая величина крутящего момента для вращения груза измеряется следующим образом:

                                                  Крутящий момент = Сила x перемещение

                                                  25 Н x 0.07 м = 1.4 Нм

Теперь измеряем крутящий момент от оборотов без мощности.

Как рассчитать крутящий момент изоборотов без питания?

Не существует формулы для расчета крутящего момента только с использованием оборотов и без учета мощности.

С помощью прибора, называемого тахометром, мы можем найти тахометр по формуле.

                                                    P = об/мин х крутящий момент

В случае поступательного движения фургона для измерения силы можно использовать меру лобового сопротивления.

Даже в этом случае мы можем измерить силу, используя доступные величины. Но, в конечном счете, нам нужно знать величину мощности, чтобы можно было легко и быстро измерить крутящий момент.

Научиться измерять крутящий момент без угла.

Как записатьсярассчитать крутящий момент без угла?

Один из методов расчета крутящего момента без использования угла можно измерить, как показано ниже.

Приложение силы к точке поворота груза при вращательном движении можно измерить с помощью синусоидального угла. Но если сила не приложена к точке поворота, мы можем измерить величину крутящего момента, действующего на нее, используя формулу, которая содержит приложенную силу в ньютонах, умноженную на длину смещения от оси вращения.

Теперь, чтобы подробно разобраться в различиях между крутящим моментом и мощностью.

Напишите разницу между крутящим моментом и мощностью?

Основные различия между крутящим моментом и мощностью указаны в таблице ниже.

Атрибуты	Крутящий момент	Питания
Смысл	Это форма силы, которая помогает объекту двигаться по траектории вращения. .	Помогает узнать объем работы, выполненной на объекте
Количество	вектор	скаляр
Единица СИ	Ньютон-метр / Фунт-фут	Ватт
Уравнение	Крутящий момент = сила x радиус	Мощность = крутящий момент x угловая скорость
Прибор, используемый для измерения	Датчик крутящего момента / измеритель крутящего момента	Мультиметр / счетчик энергии

Теперь знать, как крутящий момент меняется с оборотами.

Проблемы, связанные с крутящим моментом и частотой вращения

Вот некоторые из проблемы, основанные на крутящем моменте и об/мин.

Проблема 1
Вал вращался со скоростью 200 об/мин, и на него подавалась мощность 36 кВт. Измерить общий крутящий момент, действующий на вал?Изображение кредита: Бесплатные изображения Pixabay

Решение: Сначала дайте нам знать формулу расчета мощности

Мощность = работа / время = сила х перемещение / время

Мощность (измеряется в ваттах) = крутящий момент (измеряется в Нм) x угловая скорость (Измеряется в рад/с)

Р = τ ω

Мощность (Вт) = 36 кВт (1000) = 36 000 Вт

Угловая скорость (измеряется в рад/сек) = 200 об/мин (2 pi)/60 сек.

Угловая скорость (измеряется в рад/сек) = 200 об/мин (2 x 3.142)/60 сек = 20.94 рад/сек

Р/ю = т

36 000 Вт / 20.94 (рад/сек) = τ = 1791 Нм

Следовательно, полученный крутящий момент составляет 1791 Нм.

Проблема 2
Вал вращается со скоростью 360 об/мин, и на него передается мощность 52 кВт. Рассчитайте суммарную величину крутящего момента, действующего на вал?Изображение кредита: Бесплатные изображения Pixabay

Решение: Сначала дайте нам знать формулу расчета мощности

Мощность = работа / время = сила х перемещение / время

Мощность (измеряется в ваттах) = крутящий момент (измеряется в Нм) x угловая скорость (измеряется в рад/сек)

Р = τ ω

Мощность (Вт) = 52 кВт (1000) = 52 000 Вт

Угловая скорость (измеряется в рад/сек) = 360 об/мин (2 pi)/60 сек.

Угловая скорость (измеряется в рад/сек) = 360 об/мин (2 x 3.142) / 60 сек = 37.70 рад/сек

Р/ю = т

52 000 Вт / 37.70 (рад/сек) = τ = 1379 Нм

Следовательно, полученный крутящий момент составляет 1379 Нм.

Проблема 3
Вал вращается со скоростью 460 об/мин, и на него передается мощность 45 кВт. Какой крутящий момент действует на вал?Изображение кредита: Бесплатные изображения Pixabay

Решение: Сначала дайте нам знать формулу расчета мощности

Мощность = работа / время = сила х перемещение / время

Мощность (измеряется в ваттах) = крутящий момент (измеряется в Нм) x угловая скорость (измеряется в рад/сек)

Р = τ ω

Мощность (Вт) = 45 кВт (1000) = 45 000 Вт

Угловая скорость (измеряется в рад/с) = 460 об/мин (2 pi)/60 с

Угловая скорость (измеряется в рад/сек) = 460 об/мин (2 x 3.142) / 60 сек = 48.17 рад/сек

Р/ю = т

46 000 Вт / 48.17 (рад/сек) = τ = 954 Нм

Следовательно, полученный крутящий момент составляет 954 Нм.

Часто задаваемые вопросы | FAQs
Isкрутящий момент всегда похож на энергию?

Если записать в основных единицах системы СИ, крутящий момент и энергия получат одинаковые размерности.

Несмотря на то, что их размеры одинаковы, они не могут иметь одинаковую меру при расчете для одного и того же материала. Еще одно отличие состоит в том, что крутящий момент является одной из важных векторных величин и его всегда можно увидеть при вращательном движении.

Можно ли сказать, что крутящий момент всегда равен работе?

Крутящий момент — это другая величина по сравнению с работой.

Как мы можем измерить крутящий момент, используя единицу СИ?

Для измерения крутящего момента можно использовать два типа единиц измерения, которые приведены ниже:

Первая единица — ньютон-метры, где ньютон относится к силе, приложенной к объекту, а метр, вообще говоря, указывает длину руки при вращательном движении. Другой единицей измерения является фунт-фут, аналогичный Нм.

Назовите важное устройство, которое используется для измерения крутящего момента?

Ниже приведен один из основных инструментов или устройств, используемых для измерения крутящего момента.

Плоская спиральная пружина — это такой инструмент, который используется физиками для измерения количества крутящий момент, испытываемый вращающимся объект.

Упомяните связь между крутящим моментом и оборотами в минуту?

Крутящий момент — это мера силы во вращательном движении, а число оборотов в минуту — это количество оборотов в этом вращении.

И крутящий момент, и число оборотов в минуту могут быть связаны друг с другом по формуле, используемой для измерения крутящего момента. Крутящий момент обязательно является силой, используемой для вращения шестерен в двигателе. Крутящий момент обратно пропорционален оборотам, когда он измеряется в лошадиных силах.

Счет, математика и статистика — набор академических навыков

Моменты (механика)

ContentsToggle Main Menu 1 Моменты 2 Рабочий пример: нахождение момента 3 Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 4 Рабочий пример: тела покоятся в равновесии

Моменты

Вращающее действие силы на тело, на которое она действует, измеряется моментом силы.

Момент силы зависит от величины силы и расстояния от оси вращения.

Момент силы относительно точки равен (величина силы) $\times$ (перпендикулярное расстояние линии действия силы от точки).

Когда на тело действует несколько сил, моменты относительно точки могут складываться, если задано положительное направление (по часовой стрелке или против часовой стрелки) и учитывается для каждого момента.

Работал Пример: Нахождение момента

Нахождение момента $F$ около $P$

9{\circ}), \\ &= 64,241\mathrm{Нм} \text{ (до 3д.п.).} \end{align} Момент силы измеряется в ньютон-метрах $\mathrm{Н м }$, поэтому момент $F$ относительно $P$ равен $64,241\mathrm{Nm}$.

Сумма моментов

На схеме показан набор сил, действующих на световой стержень. Вычислите сумму моментов относительно точки $P$.

Решение

Каждая сила уже перпендикулярна точке $P$.

Момент силы $6\mathrm{N}$ равен $6 \times 2 = 12 \mathrm{N m}$ против часовой стрелки.

Момент силы $14\mathrm{N}$ равен $14 \times 2 = 28 \mathrm{N m}$ по часовой стрелке.

Момент силы $5\mathrm{N}$ равен $5 \times (2+3) = 25 \mathrm{Nm}$ против часовой стрелки.

Всего по часовой стрелке $= 28 \mathrm{N m}$ и всего против часовой стрелки $= 37 \mathrm{Nm}$. Следовательно, сумма моментов равна $37 — 28 = 9 \mathrm{Nm}$ против часовой стрелки. Поскольку сумма против часовой стрелки была больше, мы выбрали против часовой стрелки в качестве положительного направления.

Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 9{\circ}), \\ & = 66,684 \mathrm{Nm} \text{ против часовой стрелки (3 д.п.).} \end{align}

Пример работы: Тела, находящиеся в равновесии

Нахождение нормальных реакций

Предположим, что имеется однородный стержень длины $9\mathrm{m}$ и веса $30\mathrm{N}$. Он опирается на опору $X$ одним концом и опору $Y$, которая находится на расстоянии $5\mathrm{m}$ от опоры $X$. Рассчитайте величину реакции на каждой из опор.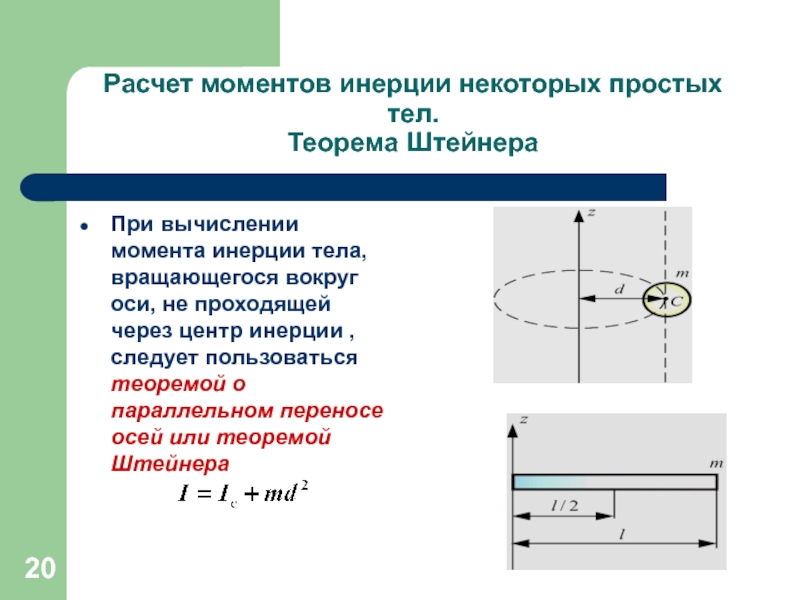

Решение

Мы можем нарисовать схему, показывающую все действующие силы.

Вес стержня будет действовать в его центре масс — так как это однородный стержень, вес действует в средней точке. Стержень находится в равновесии, поэтому суммарные силы, действующие вверх, будут равны суммарным силам, действующим вниз, когда мы разрешим вертикально. \begin{equation} R_X + R_Y = 30. \end{equation} Рассмотрим моменты относительно точки $X$, мы имеем, что моменты по часовой стрелке будут равны моментам против часовой стрелки, поэтому \begin{align} 30 \times 4.5 & = R_Y \times ( 4,5 + 0,5), \\ 135 & = 5R_Y, \\ 27 \mathrm{N} & = R_Y. \end{align} Теперь мы можем использовать это значение, чтобы найти $R_X$ \begin{align} R_X + R_Y & = 30, \\ R _ X & = 30 — 27, \\ & = 3 \mathrm{N}. \end{align} Следовательно, реакция в точке $X$ равна $3 \mathrm{N}$, а реакция в точке $Y$ равна $27\mathrm{N}$.

Нахождение центра масс неоднородного тела

Предположим, что имеется неоднородный стержень $AB$ длины $10\mathrm{m}$ и веса $15\mathrm{N}$. Он находится в горизонтальном положении и опирается на опоры в точках $C$ и $D$. Расстояние $A C = 3m$ и $AD = 7m$. Величина реакции при $C$ в четыре раза превышает величину реакции при $D$. Найдите расстояние центра масс стержня от $A$.

Решение

Мы можем нарисовать схему, показывающую все действующие силы.

Здесь мы предположили, что центр масс действует в точке $x$ m из точки $A$. Поскольку стержень не является однородным, мы не можем сказать, что центр масс находится в середине стержня. Разрешаем по вертикали \begin{align} 4R + R & = 15, \\ 5R & = 15, \\ R & = 3. \end{align} Теперь возьмем моменты относительно точки $A$ \begin{align} 15 \ x & = (4R \times 3) + (R \times 7), \\ & = 36 + 21, \\ & = 57, \\ x & = 3,8. \end{align} Центр масс $3,8 \mathrm{m}$ от $A$.

Что такое момент?

Что такое момент?




Что такое момент?

---

Момент силы является мерой его стремления заставить тело вращаться вокруг определенной точка или ось.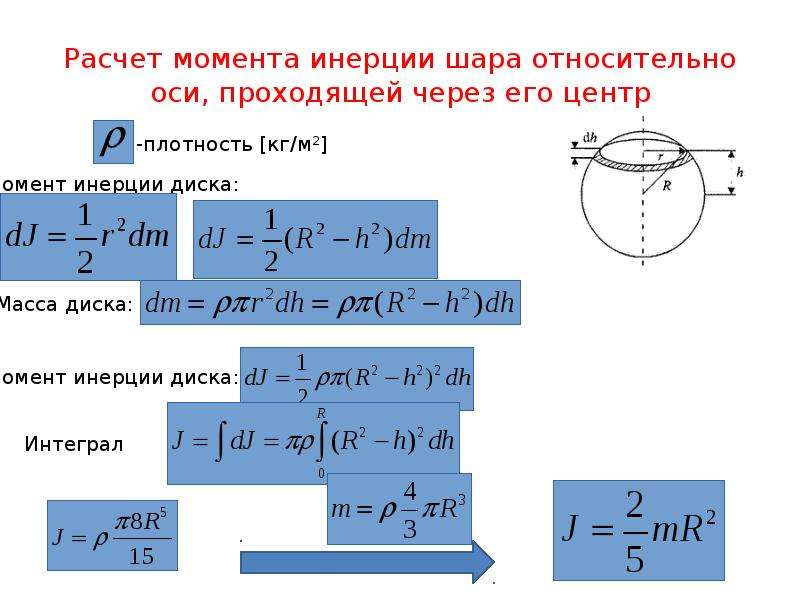

Это отличается от стремления тела двигаться или перевести, в направлении силы. Чтоб на мгновенье развиться, сила должна действовать на тело таким образом, чтобы тело начало крутить. Это происходит каждый раз, когда прикладывается сила, так что она не проходят через центр тяжести тела. Момент возникает благодаря силе, не имеющей равная и противоположная сила прямо вдоль ее линии действия.

Представьте, что два человека толкают дверь за ручку с противоположных сторон. Если оба они толкают с одинаковой силой, то возникает состояние равновесие. Если бы кто-нибудь из них вдруг отскочил от двери, толчок другого человека больше не будет иметь никакого противодействия, и дверь отмахивался бы. Человек, который все еще толкал дверь, создал момент.


---

Элементы момента

Величина момента силы, действующей относительно точки или оси, равна прямо пропорционально расстоянию силы от точки или оси. Он определяется как произведение силы (F) и плеча момента (d).

плечо момента или плечо рычага — это перпендикулярное расстояние между линия действия силы и центр моментов.


Момент = Сила x Расстояние или M = (Ф)(г)

Центр моментов может быть фактической точкой, относительно которой сила вызывает вращение. Это также может быть точка отсчета или ось, вокруг которой сила может рассматриваться как вызывающая вращение. Это не имеет значения, пока поскольку конкретная точка всегда принимается за точку отсчета. Последний случай гораздо более распространенная ситуация в задачах проектирования конструкций.

Момент выражается в футо-фунтах, тысячах футов, ньютон-метры или килоньютон-метры. Момент тоже имеет смысл; по часовой стрелке вращение вокруг центра моментов будет считаться положительным моментом; а вращение против часовой стрелки вокруг центра моментов будет считаться отрицательный. Самый распространенный способ выразить момент —


.

 

---


В примере показано, как гаечный ключ крепится к гайке. Сила в 100 фунтов равна применяется к нему в точке C, центре гайки. Сила приложена в x-расстояние 12 дюймов от гайки. Центр моментов может быть точка C, но также могут быть точки A, B или D.

Момент вокруг точки C
Плечо момента для расчета момента вокруг точки C составляет 12 дюймов. величина момента относительно точки C равна 12 дюймам, умноженным на силу 100 фунтов, чтобы дать общий момент 1200 дюймов-фунтов (или 100 фут-фунтов).

Рычаг момента (d) = 12 дюймов

Величина (F) = 100 фунтов

Момент = M = 100 фунтов x 12 дюймов = 1200 дюйм-фунтов

Точно так же мы можем найти моменты относительно любой точки пространства.

Момент @	А	Б	D
Моментный рычаг	8 дюймов	2 дюйма	0 дюймов
Величина F	100 фунтов	100 фунтов	100 фунтов
Общий момент	800 дюймов-фунтов	200 дюймов-фунтов	0 дюймы-фунты

Момент вызывает вращение вокруг точки или оси. Если момент быть взято около точки благодаря силе F, то для того, чтобы на момент развиться, линия действия не может проходить через эту точку. Если линия действия проходит через эту точку, момент равен нулю, потому что величина плечо момента равно нулю. Так было с точкой D в предыдущем гаечном ключе. проблема. Суммарный момент равен нулю, потому что плечо момента также равно нулю.


В качестве другого примера предположим, что сила в 200 фунтов приложена к ключ, как указано. Момент силы в 200 фунтов, приложенной в точке С, равен нулю. потому что:

M = F x d = 200 фунтов x 0 дюймов = 0 дюймов-фунтов

Другими словами, сила в 200 фунтов не вызывает ключ для вращения гайки. Можно было бы увеличить величину силы пока болт окончательно не сломался (разрушение при сдвиге).

Момент вокруг точек X, Y и Z также будет равен нулю, потому что они также лежат на линии действия.



Момент также можно рассматривать как результат действия сил, отклоняющихся от прямая линия, проведенная между точкой загрузки системы и ее опорами. В этом случае синяя сила является эксцентрической силой. Для того, чтобы оно достигло основание колонны, она должна делать обход через балку. Чем больше объезд, тем больше момент. Наиболее эффективные структурные системы иметь наименьшее количество обходных путей. Это будет обсуждаться более подробно в Лекции 37 и более поздние курсы.

Есть случаи, когда проще вычислить моменты компоненты силы вокруг определенной точки, чем вычислить момент самой силы. Возможно, определение перпендикуляра расстояние действия силы сложнее, чем определение перпендикуляра расстояние компонентов силы. Момент нескольких сил о точка — это просто алгебраическая сумма составляющих их моментов относительно тот же пункт. При сложении моментов составляющих необходимо принимать большие заботиться о том, чтобы соответствовать смыслу каждого момента. Часто это благоразумно отметить смысл рядом с моментом, когда берутся за такие задачи.

Комбинированный Моменты
Моменты на балке

---

Распространенные ошибки
При добавлении моментов компонентов необходимо проявлять большую осторожность, чтобы быть последовательными со смыслом каждого момента.