Вращающий момент | это… Что такое Вращающий момент?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе

Содержание 1 Момент силы 2 Предыстория 3 Единицы 4 Специальные случаи 4.1 Формула момента рычага 4.2 Сила под углом 4.3 Статическое равновесие 4.4 Момент силы как функция от времени 5 Отношение между моментом силы и мощностью 6 Отношение между моментом силы и работой 7 Момент силы относительно точки 8 Момент силы относительно оси 9 Единицы измерения 10 Измерение момента 11 См. также

Момент силы

В физике момент силы можно понимать как «вращающая сила».

В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться.

Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

• Момент инерции
• Момент импульса
• Теорема Вариньона

Вращающий момент | это… Что такое Вращающий момент?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе

Содержание 1 Момент силы 2 Предыстория 3 Единицы 4 Специальные случаи 4.1 Формула момента рычага 4.2 Сила под углом 4.3 Статическое равновесие 4.4 Момент силы как функция от времени 5 Отношение между моментом силы и мощностью 6 Отношение между моментом силы и работой 7 Момент силы относительно точки 8 Момент силы относительно оси 9 Единицы измерения 10 Измерение момента 11 См. также

Момент силы

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться.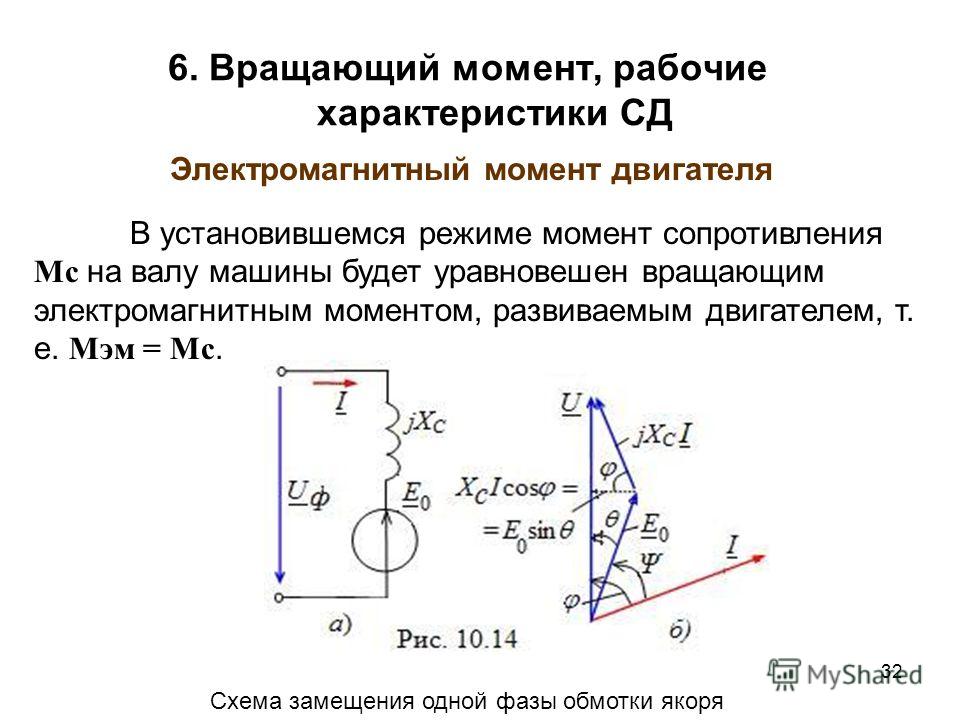 Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

• Момент инерции
• Момент импульса
• Теорема Вариньона

Крутящий момент | Уравнение, определение и единицы измерения

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Torque (2004) — IMDb

• Актеры и съемочная группа
• Отзывы пользователей 37 PG-13
• 1ч 24м

РЕЙТИНГ IMDb

4. 1/10

29K

ВАША ОЦЕНКА

Воспроизвести трейлер2

:

31

12 Видео

29 Фото

ActionComedyCrime

Байкер возвращается из Таиланда, чтобы разобраться со своей девушкой. Один лидер банды хочет, чтобы он доставил 2 мотоцикла, наполненных кристаллическим метамфетамином, а другой лидер банды хочет, чтобы он… Читать всеБайкер возвращается из Таиланда, чтобы уладить отношения со своей девушкой. Один лидер банды хочет, чтобы он доставил 2 мотоцикла, наполненных кристаллическим метамфетамином, а другой лидер банды хочет, чтобы он убил своего брата. Байкер возвращается из Таиланда, чтобы уладить отношения со своей девушкой. Один лидер банды хочет, чтобы он доставил 2 мотоцикла, наполненных кристаллическим метамфетамином, а другой лидер банды хочет, чтобы он убил своего брата.

• Режиссер
  • Джозеф Кан
• Сценарист
  • Мэтт Джонсон
• Звезды
  • Мартин Хендерсон
  • Ice Cube
  • Monet Mazur

См. производство, кассовые сборы и информацию о компании

IMDb РЕЙТИНГ

4.1/10

29K

ВАШ РЕЙТИНГ

• Режиссер
  • Джозеф Кан
• Сценарист
  • Мэтт Джонсон
• Звезды
  • Мартин Хендерсон
  • Ice Cube
  • Моне Мазур

• 229Отзывы пользователей
• 88Критические обзоры
• 41Metascore

Подробнее на IMDbPro

• Награды
  • 4 номинации

Видео12

Трейлер 2:31

Смотреть Крутящий момент Трейлер

Трейлер 0:31

Смотреть Крутящий момент

Клип 0:56

Смотреть Torque Scene: Тебе не понравится, чем это закончится 1:14

Смотреть Torque Scene Это должно быть неприятно

Clip 1:03

Смотреть Torque Scene: Меня подставили

Clip 1:11

Смотреть Torque Scene: Damn You Ford

Clip 1: 04

Смотреть сцену с крутящим моментом: ты связался не с той цыпочкой

Клип 0:58

Смотреть Крутящий момент: Погоня за поездом

Клип 0:45

Смотреть Крутящий момент.

Клип 1:06

Смотреть Torque Scene: Я говорю тебе, сделай это правильно

Джон Эшкер

• Желтый водитель автомобиля

Макс Бизли

• Лютер

Дейн Кук

• Нил Лафф

Джон Доу

• Шериф Барнс

Гичи Гамба

Лэнс Гилберт

• 18 Уилер Драйвер

Джей Эрнандес

• Далтон

Уилл Юн Ли

Фэйзон Лав

Юстина Мачадо

• Хендерсон

Хейден МакФарланд

Кристина Милиан

Кинга Филипс

• Подруга Нила Лаффа

Джейми Прессли

Николь Галисия

• Микиша
• (как Николь Мерседес Робинсон)

• Директор
  • Джозеф Кан
• Сценарист
  • Мэтт Джонсон
• Весь актерский состав и съемочная группа
• Производство , кассовые сборы и многое другое на IMDbPro

Больше похоже на это

Biker Boyz

xXx

Следующий уровень

xXx: State of the Union

Автомобиль 19

Крутящий момент

Колыбель 2 Могила

Герцоги Хаззарда

ХХХ: Возвращение Ксандера Кейджа

Однажды в Мексике

Рожденные для гонок

С телом

Сюжетная линия

Вы знаю

• Цитаты

  Шейн: [Шейн и Форд едут на серийной гоночной машине] Форд, пробка!

  Кэри Форд: Ой! Вот почему я ненавижу четыре колеса!

• Связи

  Показан в Шоколад: Глубокие темные секреты (2005)

• Саундтреки

  Someday
  Написано Чадом Крюгером, Майком Крюгером (в роли Майкла Крюгера), Райаном Пиком и Райаном Викедалом 27

  Отзывы пользователей229

  Обзор

  Избранный обзор

  4 /

  10

  Только для самых безбашенных фанатиков байкеров

  Весь замысел этого фильма — заработать деньги. С самого начала фильм выглядит просто переработанным. Когда я настроился, я даже подумал, что это какая-то реклама, и я был прав, потому что весь этот фильм, по сути, реклама мотоциклов. То, как надпись в начале гласит «машины отстой», комментарии на протяжении всего фильма «вот почему я ненавижу 4 колеса!». Это довольно очевидно, хотя вы не можете серьезно относиться к таким вещам.

  В этом фильме тоже много ошибок, но что мне не понравилось в этом фильме, так это то, что он слишком много внимания уделяет мотоциклам и транспортным средствам. Поверьте мне, когда я говорю, что это не что иное, как люди, соревнующиеся друг с другом с очень тонким сюжетом о парне, которого обвиняют в убийстве, которого он не совершал. Это в основном вся предпосылка этого фильма, поэтому, если вы не любите велосипеды и автомобили (да, такие люди существуют), то вы можете вычеркнуть этот фильм из своего списка прямо сейчас.

  Одним из аспектов, который был не так уж плох, было использование компьютерной графики для создания ощущения гипердрайва во время некоторых сцен вождения/погони. Но опять же, это быстро похоже на рекламу велосипеда. Черт, они могли бы вставить логотип Yamaha в конце вождения в Torque, и все готово; идеальный рекламный ролик.

  Персонажи также ничем не отличаются от типичных голливудских персонажей, и они так же тонки, как и сюжет, который они представляют. Актерская игра могла бы быть и хуже, но диалоги — самая ужасная и смехотворная чепуха, которую вы когда-либо слышали. Если велосипеды — это ваша жизнь, и вы всегда хотели что-то вроде «Форсажа», но с велосипедами, тогда попробуйте, если вы хотите хороший фильм, просто избегайте этого.

  полезно•3

  1

  • morkulv_athferion
  • 12 февраля 2009 г.

  Лучшие подборки

  Войдите, чтобы оценить и посмотреть список для персональных рекомендаций 9 0123

  Войти

  Подробнее

  • Дата выпуска
    • 16 января , 2004 (США)
  • Страна происхождения
    • США
  • Официальный сайт
    • Официальный сайт
  • Язык
    • Английский
  • Также известен как
    • Bá Chủ Đường Đua
  • Места съемок
    • Блайт, Калифорния, США
  • Производственные компании
    • Warner Bros.
    • Village Roadshow Pictures
    • Оригинальный фильм
  • См. больше кредитов компании на IMDbPro

  Кассовые сборы

  • Бюджет
    • 40 000 000 долларов США (приблизительно)
  • Валовой доход США и Канада
    • 21 215 059 долл. США
  • Выходные дни США и Канады
    • 9 970 557 долл. США
    • 18 января 2004 г.
  • Gros s по всему миру
    • $46 546 197
  См.