Как правильно поворачивать на автомобиле, техника выполнения поворотов — Autodromo

Больше всего сложностей у водителей-новичков, наряду с обгоном и парковкой, вызывает выполнение поворотов, а ведь именно поворот является одним из важных элементов управления автомобилем.

Практически любой, совершаемый маневр автомобилем на дороге, может являться поворотом (с определенной долей натяжки, конечно). Именно поэтому так важно научиться поворачивать на автомобиле во время движения.

Правильный поворот должен быть точным, быстрым, безопасным и выполняться по всем правилам.

Содержание

Техника выполнения поворота

Прежде чем приступить к освоению техники поворота, следует знать о том, что любой поворот выполняется в четыре приема:

1. Движение по прямой – приближение к повороту;
2. Вхождение в поворот, сопровождается поворачиванием руля;
3. Движение в повороте;
4. Выход из поворота, сопровождается установкой руля в исходное положение.

Далее любое движение на автомобиле происходит прямолинейно до следующего поворота. Для того чтобы выполнить безопасный поворот, важно учитывать основные факторы, влияющие на данный процесс – рабочий режим двигателя, скорость и траекторию движения в повороте.

Траектория движения в повороте

При проведении любого поворота важно учитывать траекторию движения автомобиля в дуге поворота. Траектория движения выполняется строго по правилам на полосе движения без дополнительных манипуляций рулем.

Таким образом, при вхождении в поворот, выкручиваем руль в сторону поворота, проходим по дуге, возвращаем руль в исходное положение и продолжаем прямолинейное движение.

Скорость движения в повороте

Вхождение в поворот должно происходить на сниженной скорости. Перед любым поворотом (именно перед поворотом, а не во время поворота) следует сбросить скорость, а по дуге продолжать движение уже на постоянной скорости.

Для безопасности водителя снижение скорости должно происходить на прямом участке дороги на приближении к повороту, для того чтобы избежать проскальзывания колес, торможения или заноса всего корпуса автомобиля.

Вкратце мы рассмотрели, что следует учитывать при приближении к повороту – это скорость и траектория движения. А сейчас более детально о действиях водителя при вхождении в поворот, движении в повороте и выходе из поворота.

Вхождение в поворот

Приближение и вхождение в поворот должно происходить на сниженной скорости. Скорость движения рассчитывается с учетом угла и радиуса поворота, а также состояния дороги. При неблагоприятных условиях, скорость движения должна быть гораздо ниже, чем в обычных условиях.

При вхождении в поворот следует учитывать еще два момента – точку фиксации внимания и положение рук на руле.

При выполнении поворота вы должны фиксировать свое внимание на том участке дороги, куда направляетесь. В перспективе, это должна быть точка выхода из поворота (если поворот не слишком крутой).

Таким образом, поворачивая руль при вхождении в поворот, взгляд должен быть устремлен на тот участок, где вы вернете руль в исходное положение. В идеале взгляд должен плавно скользить по всему участку движения вашего автомобиля, для того чтобы рассчитывать не только скорость движения, но и расстояние.

Если же точка выхода из поворота не просматривается, в таком случае преодоление дуги поворота должно проходить только на сниженной скорости.

Что касается положения рук на руле, здесь все просто. Перед вхождением в поворот необходимо переместить руки на участок руля, который находится в противоположной стороне от направления поворота. Наиболее оптимальным положением рук при левостороннем повороте является схема – 4/12, при правостороннем – 8/12.

Для пояснения схемы расположения рук представим, что руль разбит на отдельные участки и представляет собой циферблат. Первое значение – это участок, на котором располагается правая рука, второе значение – расположение левой руки. Таким образом, на цифре 4 находится правая рука, на цифре 12 – левая рука.

Важно помнить, что ладони необходимо всегда держать на руле, для изменения положения руки (или хвата) применяется тактика скольжения по рулю.

Движение в повороте

Двигаясь в дуге поворота, категорически запрещается резкое изменение скорости движения.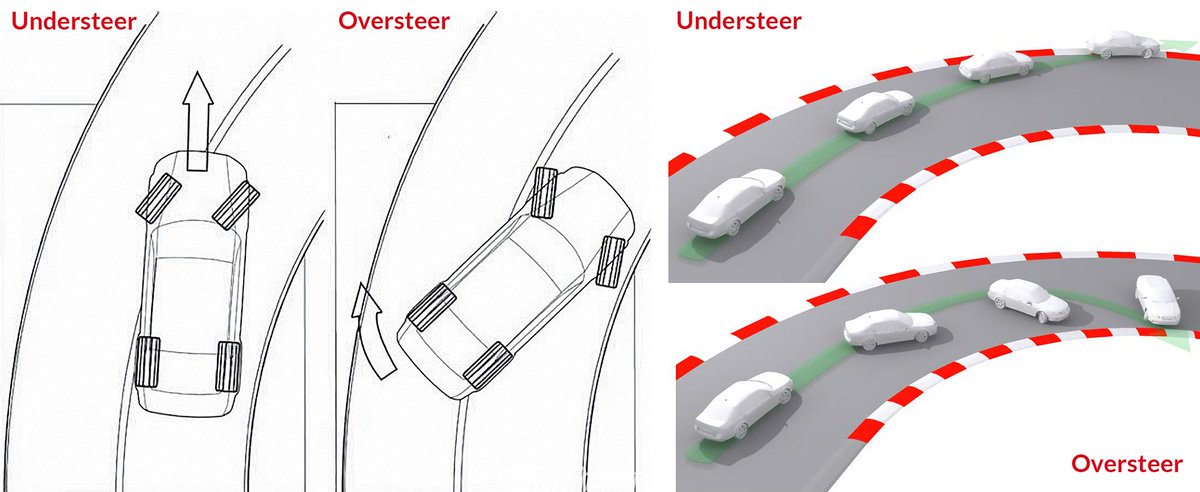 Поэтому движение в повороте должно происходить исключительно на постоянной скорости.

Тормозить на дуге прохождения поворота можно только в экстренных случаях, когда, к примеру, водитель не может справиться с вождением на установленной скорости, что чревато заносом или вылетом автомобиля на обочину. В таких случаях торможение должно быть плавным и медленным.

Выход из поворота

Окончание движения по дуге поворота с выходом на прямой участок дороги сопровождается выравниванием руля и плавным набором скорости. При этом разгон должен происходить плавно для того чтобы избежать потери контроля над управлением транспортным средством и выездом на встречную полосу.

Резюмируя все вышесказанное можно представить полную схему осуществления любого поворота.

1. При подъезде к повороту водитель плавно выжимает тормозную педаль, чтобы снизить скорость, при необходимости переключаясь на более низкую передачу.
2. На входе в поворот водитель определяет траекторию и полосу движения автомобиля. Поворот руля осуществляется двумя руками, которые находятся в положении, согласно схеме захвата. Взгляд фиксируется на точке выхода из поворота. Войдя на дугу, в повороте поддерживается постоянная скорость движения.
3. При выходе из поворота водитель возвращает руль в исходное положение и начинает плавно увеличивать скорость движения. При прямолинейном движении происходит полный разгон скорости с переключением на высокую передачу.

На самом деле, немного потренировавшись, все новички довольно быстро осваивают технику прохождения поворотов и вскоре начинают чувствовать некоторую самоуверенность, переоценивая свое водительское мастерство, позволяя себе определенные вольности.

Как вы понимаете, это чревато неприятными последствиями. Дорога ошибок не прощает, поэтому очень важно, особенно для новичков, держать себя в руках и помнить о правилах прохождения поворотов.

Со временем, набравшись опыта, вы уже не будете задумываться о том, как держать руль, с какой скоростью двигаться, когда жать на педаль и так далее, все это будет происходить автоматически на уровне чувств.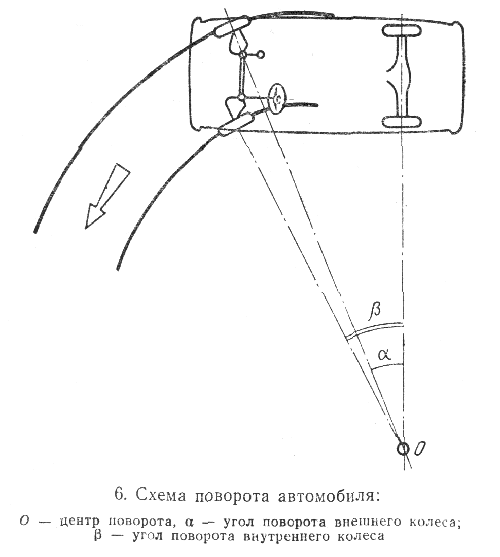 Главное в этом, выработать на стадии обучения правильную технику прохождения поворотов, чтобы в будущем ездить безопасно.

Во второй части видео-ролика идет реклама Мерседеса, но про поворот рассказывается неплохо:

Геометрия поворота / Этюды // Математические этюды

Геометрия поворота / Этюды // Математические этюды

Математические этюды

К списку

Парал­лельны ли друг другу перед­ние колёса автомо­биля при пово­роте?

Ока­зы­ва­ется, что именно геомет­рия и меха­ника опре­де­ляют то, как надо пово­ра­чи­вать колёса автомо­биля.

Если про­долже­ние оси колёс направ­лено в центр пово­рота, то колесо остав­ляет чёт­кий след. Чёт­кая кар­тинка будет, и если несколько осей направ­лены в центр пово­рота. Однако, если про­долже­ние оси колеса направ­лено не в центр пово­рота, то колесо катится с про­скаль­зы­ва­нием. След будет стёр­тым, а самое глав­ное, управ­ля­емость транспорта с таким коле­сом будет тем хуже, чем выше ско­рость. Итак, для хорошей управ­ля­емо­сти про­долже­ния осей колес должны быть направ­лены в центр пово­рота. Что же это зна­чит для четырёх­ко­лёс­ного автомо­биля?

Научимся для начала про­хо­дить про­стой пово­рот — дугу окруж­но­сти.

Так как зад­ние колёса в большин­стве машин не пово­ра­чи­ваются, то центр окруж­но­сти пово­рота должен лежать на про­долже­нии оси этих колёс. Перед­ние колёса необ­хо­димо повер­нуть так, чтобы про­долже­ние оси каж­дого колеса смот­рело в этот же центр. А зна­чит, для хорошей управ­ля­емо­сти перед­ние колёса необ­хо­димо пово­ра­чи­вать на раз­ные углы, и они будут непа­рал­лельны!

Вы скажете, что пово­роты не все­гда являются дугой какой-либо окруж­но­сти, и уж тем более машина не оста­нав­ли­ва­ется для того, чтобы повер­нуть колёса. Это, конечно, правда, но ока­зы­ва­ется, что при любом пово­роте в каж­дый момент времени можно счи­тать, что машина едет по дуге неко­то­рой окруж­но­сти (радиус и центр кото­рой зави­сят от момента времени).

Рас­смот­рим про­из­воль­ную дорогу. Чтобы по ней можно было ездить, у неё не должно быть ост­рых углов, т.е. сред­няя линия будет, как гово­рят в матема­тике, глад­кой кри­вой.

Зафик­си­руем синюю точку на сред­ней линии и подумаем, каким более про­стым геомет­ри­че­ским объек­том можно заме­нить кри­вую в небольшой окрест­но­сти нашей точки.

Возьмём про­из­воль­ную крас­ную точку неда­леко от синей. Две точки на плос­ко­сти опре­де­ляют един­ствен­ную прямую, кото­рую и про­ве­дём. Будем двигать крас­ную точку по кри­вой к синей. В момент, когда они совпа­дут, прямая, ими опре­де­ля­емая, будет каса­тель­ной прямой. Она даёт линей­ное при­ближе­ние кри­вой дороги в небольшой окрест­но­сти зафик­си­ро­ван­ной точки. Однако при уве­ли­че­нии видно, что дорога и каса­тель­ная прямая рядом идут на очень маленьком участке.

Справа и слева от синей точки возьмём по крас­ной. Три точки, не лежащие на одной прямой, опре­де­ляют един­ствен­ную окруж­ность, кото­рую и про­ве­дём.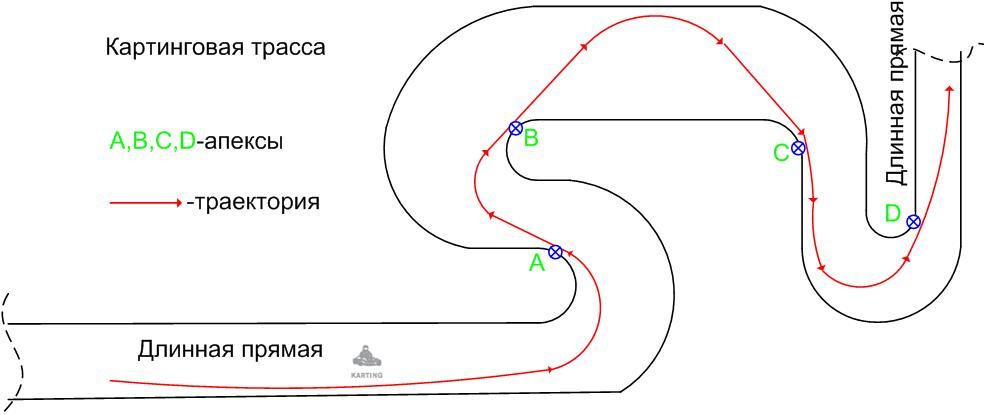

Будем двигать крас­ные точки к синей. В момент, когда они совпа­дут, полу­чим окруж­ность, кото­рая назы­ва­ется сопри­ка­сающейся. Это при­ближе­ние уже вто­рого порядка, и на уве­ли­че­нии видно, насколько оно лучше. Заме­тим, что на моно­тон­ном участке (воз­рас­та­ния или убы­ва­ния кри­вой) сопри­ка­сающа­яся окруж­ность все­гда пере­се­кает кри­вую, в отли­чие от каса­тель­ной, рас­по­ложен­ной на таких участ­ках по одну сто­рону от кри­вой.

Так как сопри­ка­сающа­яся окруж­ность для нашей задачи хорошо при­ближает дорогу и может быть постро­ена в любой её точке, то движе­ние по изги­бам дороги можно рас­смат­ри­вать в каж­дый момент времени как движе­ние по дуге неко­то­рой окруж­но­сти. Мгно­вен­ные радиус и центр этой окруж­но­сти зави­сят, конечно, от той точки, в кото­рой нахо­дится машина.

Таким обра­зом, при движе­нии в про­из­воль­ном пово­роте можно счи­тать, что в каж­дый момент времени машина движется по небольшой дуге неко­то­рой окруж­но­сти.

И наш пер­вый слу­чай — пово­рот машины по дуге окруж­но­сти — основ­ной, кото­рый и нужно изу­чать.

Но как достичь того, чтобы при любом пово­роте колёс про­долже­ние осей смот­рело в мгно­вен­ный центр пово­рота?

Ока­зы­ва­ется, и здесь на помощь при­хо­дит геомет­рия, а именно извест­ная со школы рав­но­бо­кая трапе­ция — четырёх­уголь­ник, у кото­рого две сто­роны, назы­ва­емые осно­ва­ни­ями, парал­лельны между собой, а боко­вые сто­роны равны друг другу. Если пра­вильно подо­брать размеры сто­рон трапе­ции, то достига­ется небо­хо­димое для хорошего управ­ле­ния усло­вие — про­долже­ние осей перед­них колёс пере­се­ка­ется в точке, лежащей на про­долже­нии оси зад­них колёс. Эта точка и есть мгно­вен­ный центр пово­рота машины.

При­думал такое управ­ле­ние перед­ними колё­сами фран­цуз, карет­ных дел мастер Шарль Жанто (Charles Jeantand). Однако для карет, пере­двигавшихся с малыми ско­ро­стями, это было не так суще­ственно, как для машин, и изоб­ре­те­ние Жанто было забыто.

Лишь почти через три чет­верти века два отца автомо­би­ле­стро­е­ния, два немца, два инже­нера — Готт­либ Дайм­лер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изоб­ре­тая свои автомо­били, воз­вращаются к трапе­ции Жанто. В 1889 году Дайм­лер полу­чает патент на «спо­соб неза­ви­симого управ­ле­ния перед­ними колё­сами с раз­но­ве­ли­кими ради­у­сами пово­рота». А в 1893 году Бенц полу­чает патент на «устройство управ­ле­ния экипажей с тангенци­аль­ными к колё­сам окруж­но­стями управ­ле­ния». Решив задачу управ­ле­ния перед­ними пово­рот­ными колё­сами и другие важ­ные тех­ни­че­ские вопросы, Карл Бенц строит свой пер­вый знаме­ни­тый четырёх­ко­лёс­ный автомо­биль «Вик­то­рия».

С точки зре­ния стро­гой матема­тики, трапе­ция не поз­во­ляет достичь необ­хо­димого усло­вия — чтобы про­долже­ние осей перед­них колес при любом пово­роте пере­се­ка­лось в точке, лежащей на про­долже­нии зад­ней оси. При исполь­зо­ва­нии трапе­ции эта точка будет все­гда лежать чуть-чуть в сто­роне от линии зад­ней оси. Зачем же мы столько обсуж­дали трапе­цию, скажете вы? Рас­стра­и­ваться рано — про­сто не надо без­думно пере­но­сить матема­ти­че­скую строгость в тех­ни­че­ские вопросы. Чтобы точка пере­се­че­ния линий перед­них осей все­гда лежала на линии зад­ней оси, необ­хо­димо, чтобы длина меньшего осно­ва­ния трапе­ции немного меня­лась. При общей длине этого осно­ва­ния более метра необ­хо­димые изме­не­ния длины состав­ляют всего около одного сан­тиметра, а это меньше чем люфты в соеди­не­ниях и раз­решён­ные допуски при изго­тов­ле­нии.

Со времён изоб­ре­те­ния пер­вых автомо­би­лей ско­ро­сти пере­движе­ния сильно воз­росли. Уве­ли­чи­лись и тре­бо­ва­ния к управ­ле­нию перед­ними колё­сами. Кроме того, трапе­ция — это плос­кая геомет­ри­че­ская фигура. И такой спо­соб управ­ле­ния перед­ними колё­сами может исполь­зо­ваться только при зави­симой перед­ней под­веске — когда колёса жёстко свя­заны друг с другом и прямая, соеди­няющая их цен­тры, все­гда парал­лельна плос­ко­сти трапе­ции. Сей­час такое можно встре­тить на гру­зо­вых автомо­би­лях. На современ­ных лег­ко­вых автомо­би­лях под­веска колёс неза­ви­сима, т.е. они могут ходить по высоте друг отно­си­тельно друга. Для управ­ле­ния в пово­роте такими колё­сами при­ме­няются более слож­ные, уже неплос­кие шар­нир­ные меха­низмы, чаще всего с цен­траль­ным зве­ном в виде руле­вой рейки. Но их рас­чёт — это тоже задача матема­ти­ков и меха­ни­ков. А исто­ри­че­ски они так по-преж­нему и назы­ваются — руле­вой трапе­цией.

При пово­роте автомо­биля воз­ни­кает ещё один вопрос, свя­зан­ный с геомет­рией. Длина окруж­но­сти ради­уса R равна, как вы пом­ните, 2πR. Соот­вет­ственно, длина дуги, опи­рающейся на угол α окруж­но­сти ради­уса R, равна αR. При пово­роте автомо­биля по дуге окруж­но­сти внеш­нее перед­нее колесо едет по дуге окруж­но­сти большего ради­уса, чем внут­рен­нее перед­нее. Точно так же и зад­нее внеш­нее колесо опи­сы­вает дугу большего ради­уса, чем внут­рен­нее зад­нее. А раз ради­усы раз­ли­чаются, то, зна­чит, пути, про­хо­димые внут­рен­ним и внеш­ним колё­сами одной оси, должны быть тоже раз­личны. В про­тив­ном слу­чае колесо будет про­скаль­зы­вать, и управ­ля­емость автомо­биля сни­зится.

В слу­чае, когда ось неве­дущая, т.е. её колёса не тол­кают автомо­биль впе­рёд, всё про­сто: каж­дое колесо вер­тится со своей ско­ро­стью, необ­хо­димой для про­хож­де­ния нуж­ного пути без про­скаль­зы­ва­ния.

А как же сде­лать так, чтобы колёса ведущей оси, в нашем слу­чае зад­ней, с одной сто­роны, посто­янно тол­кали автомо­биль впе­рёд, а с дру­гой сто­роны, могли вращаться с раз­ными ско­ро­стями?

Помогает в этом диффе­ренциал — пред­ста­ви­тель пла­не­тар­ных меха­низмов. Пла­не­тар­ным назы­ва­ется меха­низм, у кото­рого есть сател­литы — шестерни, кру­тящи­еся вокруг подвиж­ных осей.

Вал от мотора, пройдя через коробку пере­дач, отдаёт враще­ние на «бочку». Бочка же через сател­литы пере­даёт враще­ние на левую и пра­вую полу­оси ведущей оси. Как бы ни враща­лись колёса, ско­рость бочки все­гда в два раза мед­лен­нее враще­ния вала, а сумма ско­ро­стей полу­осей равна удво­ен­ной ско­ро­сти вала.

Если машина едет по прямой и под обо­ими ведущими колё­сами оди­на­ко­вое покрытие — с оди­на­ко­вым коэффици­ен­том тре­ния, то колёса заби­рают от бочки оди­на­ко­вое коли­че­ство враще­ния, и полу­оси вращаются (колёса и их полу­оси) с оди­на­ко­вой ско­ро­стью.

Но если коэффици­енты тре­ния раз­ли­чаются, напри­мер, одна сто­рона машины выезжает с асфальта на грун­то­вую обо­чину или попа­дает на лёд, то… Как же будут себя вести колёса при про­хож­де­нии этого участка? У колёс неве­дущей оси всё про­сто: они неза­ви­симы друг от друга, им не надо тол­кать машину, и когда одно из них выка­ты­ва­ется на лёд, то пере­стаёт кру­титься, так как тре­ние с доро­гой очень маленькое.

Вот и под левое колесо ведущей оси попа­дает лёд. Справа тре­ние с асфальтом большое, а слева — со льдом — почти отсут­ствует.

Соот­вет­ственно, левому колесу вращаться гораздо проще, и оно начи­нает заби­рать на себя всё враще­ние, отда­ва­емое боч­кой на обе полу­оси. При этом сумма ско­ро­стей полу­осей, как было отме­чено выше, все­гда посто­янна, но одна полу­ось не кру­тится, а вто­рая — враща­ется очень быстро. Начать движе­ние из такого положе­ния, когда одно колесо ведущей оси поте­ряло связь с доро­гой (напри­мер, нахо­дится на льду), а другое нет — невозможно.

Каза­лось бы, одни неудоб­ства от этого диффе­ренци­ала, зачем он тогда нужен? Как раз для реше­ния задачи одно­времен­ного тол­ка­ния ведущей осью машины впе­рёд и про­хож­де­ния в пово­ро­тах ведущими коле­сами путей раз­ной длины. Каж­дое колесо берёт от диффе­ренци­ала коли­че­ство движе­ния про­порци­о­нально длине его пути, а в сумме всю энергию вала они затра­чи­вают на движе­ние машины впе­рёд.

Инже­неры посто­янно пытаются улучшить диффе­ренциал, сохра­нив его основ­ное свойство, пытаются уменьшить непри­ят­ные эффекты — каким-либо спо­со­бом не давать кру­титься полу­осям со слиш­ком большой раз­ницей ско­ро­стей.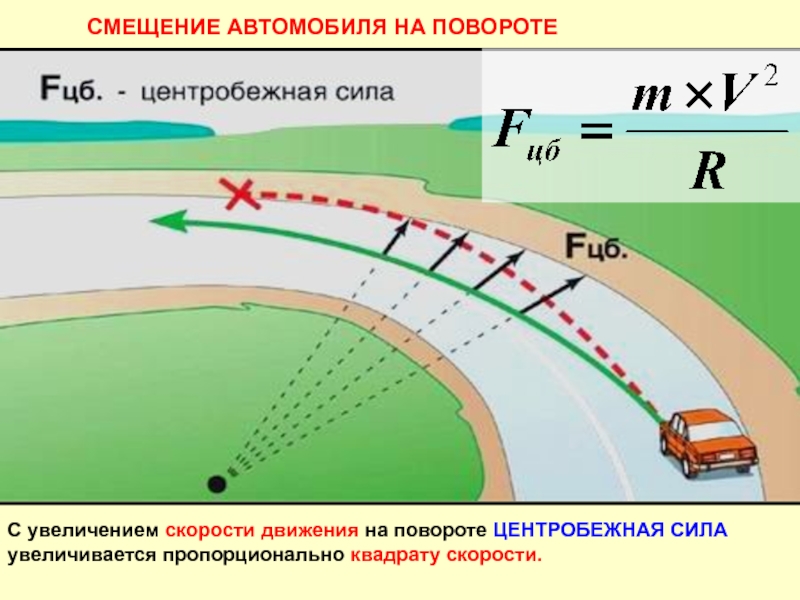 Но по сути, всё и сегодня оста­ётся таким же, ибо законы геомет­рии никто не отме­нял.

Смотри также

Пово­рот перед­них колёс автомо­биля // Матема­ти­че­ская состав­ляющая / Ред.-сост. Н. Н. Андреев, С. П. Коно­ва­лов, Н. М. Паню­нин. — Вто­рое изда­ние, расши­рен­ное и допол­нен­ное. — М. : Матема­ти­че­ские этюды, 2019. — С. 54—55, 306.

Млод­зеев­ский Б. К. К тео­рии управ­ле­ния в автомо­би­лях // Вест­ник инже­не­ров. 1917. 15 января. Т. 3, № 2. С. 37—41.

Другие этюды раздела «Математика и техника»

  Колёсная пара  Уголковый отражатель  Глубина заложения

Математические этюды

Passenger Tuptempting — размеры 180 ° и чертежи

макеты

>

Троки поворота транспортных средств

Путь поворота 180 ° для пассажирского транспортного средства измеряет минимальный радиус поворота для использования при разработке пространств для U -разворотов или разворотов на улицах, парковках, остановках или в зонах обслуживания. Для траекторий поворота можно использовать измерения от бордюра до бордюра или от стены до стены в зависимости от того, рассчитываются ли окружности поворота на основе внешней шины или внешнего переднего свеса. По возможности следует предусмотреть дополнительные зазоры для размещения автомобилей разных размеров и способностей водителей.

При измерении внутреннего и внешнего радиусов поворота на 180° минимальный внутренний радиус 14 футов 5 дюймов (4,39 м) и минимальный внешний радиус 24 фута-25 футов 6 дюймов (7,31-7,77 м) должны быть обеспечены по всему периметру. повернуть.

Траектория поворота пассажирского транспортного средства на 180° измеряет минимально возможный радиус поворота для использования при проектировании мест для разворотов или разворотов на улицах, автостоянках, съездах или в зонах обслуживания. На поворотных дорожках можно использовать либо бордюр-к-бордюру или измерения от стены до стены в зависимости от того, рассчитывается ли радиус поворота на основе внешней шины или внешнего переднего свеса.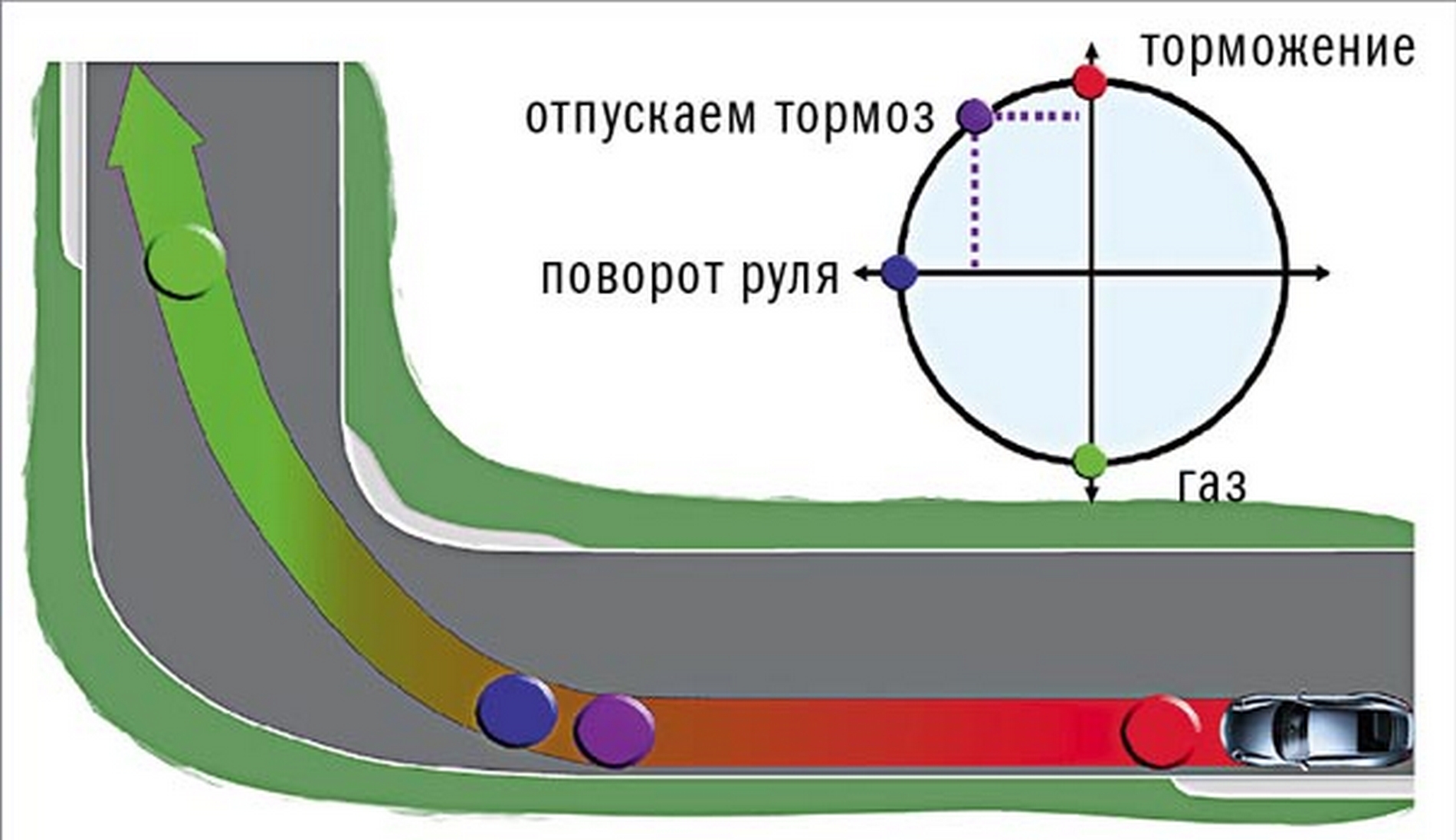 По возможности следует предусмотреть дополнительные зазоры для размещения автомобилей разных размеров и способностей водителей.

При измерении внутреннего и внешнего радиусов поворота на 180° минимальный внутренний радиус 14 футов 5 дюймов (4,39 м) и минимальный внешний радиус 24 фута — 25 футов 6 дюймов (7,31 — 7,77 м) должны быть обеспечены на всем протяжении поворота. повернуть.

Какой минимальный внутренний радиус поворота требуется для пассажирского транспортного средства, совершающего поворот на 180°?

Минимальный внутренний радиус поворота 14 футов 5 дюймов | Для пассажирского транспортного средства, совершающего разворот на 180°, должно быть предусмотрено 4,39 м.

Какой минимальный внешний радиус поворота требуется для пассажирского транспортного средства, совершающего поворот на 180°?

Внешний радиус поворота, необходимый для пассажирского транспортного средства, совершающего поворот на 180°, должен составлять не менее 24’-25’6” | 7,31-7,77 м с учетом круговой траектории, проделанной передним свесом автомобиля. По возможности следует предусмотреть дополнительное пространство.

Насколько велик типичный пассажирский автомобиль?

Средний легковой автомобиль среднего размера, обычно седан, имеет общую длину 15 футов 10 дюймов | 4,83 м и шириной 6 футов | 1,83 м.

Обновление до ProRenew Pro

*В разработке*

Высота:

Ширина:

Глубина:

Длина:

Вес:

Внешний радиус: 24’-25’6” | 7,31–7,77 м
Внутренний радиус: 14 футов 5 дюймов | 4,39 м

Колесная база автомобиля: 11’ | 3,35 м
Длина автомобиля: 19’ | 5,79 м
Ширина автомобиля: 7’ | 2,13 м

Свойства

Чертежи включают:
Траектория поворота легкового автомобиля 180° в плане

Похожие коллекции

Похожие теги

Поделиться

Text by

Брайан

Обновлено

8 апреля 2020 г.

2D Загрузки

Для загрузки этого элемента в формате 2D перейдите на членство в Dimensions Pro. Доступно в форматах DWG (CAD, Imperial и Metric), SVG, JPG

Для загрузки этого элемента в 2D продлите членство в Dimensions Pro. Доступно в форматах DWG (CAD, Imperial и Metric), SVG, JPG. Доступно в форматах 3DM (Rhino), OBJ (NURB), SKP (Sketchup) 

Для загрузки этого элемента в формате 3D продлите членство в Dimensions Pro. Доступно в форматах 3DM (Rhino), OBJ (NURB), SKP (Sketchup) 

Обновление до Dimensions ProRenew Dimensions Pro

Блокировщик рекламы

Наслаждаетесь бесплатными рисунками? Мы тоже!
Реклама помогает финансировать нашу работу.
Поддержите проект, отключив
или добавив блокировщик рекламы в белый список при просмотре Dimensions.Guide. Спасибо!

Траектория поворота пассажира — 90° Размеры и чертежи

Компоновки

>

Траектории поворота транспортных средств

Траектория поворота пассажирского транспортного средства на 90° измеряет минимально возможный радиус поворота, необходимый при проектировании парковки, погрузки и высадки. от пространств.

При измерении внутреннего и внешнего радиусов поворота на 90° необходимо обеспечить минимальный внутренний радиус 11 футов 6 дюймов (3,5 м) и минимальный внешний радиус 19 футов 2 дюйма (5,85 м). Несмотря на то, что для поворота требуется ширина всего 7 футов 6 дюймов (2,3 м), по возможности необходимо предусмотреть дополнительные зазоры, чтобы вместить большее разнообразие размеров автомобилей и способностей водителей.

Траектория поворота пассажирского транспортного средства на 90° измеряет минимально возможный радиус поворота, необходимый при проектировании парковочных, погрузочных и высадочных мест.

При измерении внутреннего и внешнего радиусов поворота на 90° необходимо обеспечить минимальный внутренний радиус 11 футов 6 дюймов (3,5 м) и минимальный внешний радиус 19 футов 2 дюйма (5,85 м). Несмотря на то, что для поворота требуется ширина всего 7 футов 6 дюймов (2,3 м), по возможности необходимо предусмотреть дополнительные зазоры, чтобы вместить большее разнообразие размеров автомобилей и способностей водителей.

Каков минимальный внутренний радиус поворота, необходимый для поворота на 90°?

Минимальный внутренний радиус поворота 11 футов 6 дюймов | 3,5 м должно быть предусмотрено для пассажирского транспортного средства, делающего 90° поворот.

Какова минимальная ширина пути для пассажирского транспортного средства, совершающего поворот на 90°?

Минимальная ширина пути поворота на 90° для легкового автомобиля составляет 7 футов 6 дюймов | 2,3 м исходя из переднего и заднего свесов типичного автомобиля.

Каков размер компактного автомобиля?

Под компактными автомобилями обычно понимаются автомобили с колесной базой менее 9 футов 2 дюймов (110 дюймов) | 2,8 м. Вместо измерения колесной базы сегодня термин компактный автомобиль относится к автомобилям с индексом внутреннего объема от 100 до 109.фут3 | 2,8-3,1 м3.

Обновление до ProRenew Pro

*В разработке*

Высота:

Ширина:

Глубина:

Длина:

Вес:

Внешний радиус: 19’2” | 5,85 м
Внутренний радиус: 11’6” | 3,5 м
Ширина прохода: 7 футов 6 дюймов | не менее 2,3 м

Колесная база автомобиля: 8’10” | 2,7 м
Длина автомобиля: 15 футов 6 дюймов | 4,74 м
Ширина автомобиля: 5 футов 9 дюймов | 1,76 м

Свойства

Чертежи включают:
Пассажирский автомобиль, поворот на 90° План пути

Связанные коллекции

Связанные теги

Поделиться

Текст

Брайан 9000 3

Обновлено

8 апреля 2020 г.