Коэффициент сопротивления сферы: что, как, примеры

В этой статье будет обсуждаться «коэффициент лобового сопротивления сферы», а также объясняться подробные факты, связанные с коэффициентом лобового сопротивления сферы. Коэффициент аэродинамического сопротивления сферы является очень важным фактором для материи.

Коэффициент аэродинамического сопротивления сферы получают как отношение площади поверхности сферы аналогичного объема для материи тела к площади поверхности материи тела. Коэффициент аэродинамического сопротивления сферы — это физический параметр, который сильно зависит от формы и размера материи.

Чему равен коэффициент сопротивления шара?Изображение – коэффициент лобового сопротивления сферы как функция числа Рейнольдса; Кредит изображения — Wikimedia Commons

Коэффициент сопротивления сферы зависит от геометрии вещества и вязкости жидкого вещества, через которое может течь вещество.

Коэффициент аэродинамического сопротивления сферы получается из-за того, что любое вещество в форме шара движется в движении через жидкое вещество, сталкивающееся с физическим параметром сопротивления. Суммарная сила приложена в том же направлении, в котором сила напряжения сдвига и давление действовали на плоскость материи.

Как рассчитать коэффициент сопротивления шара?

Давление сопротивления можно рассчитать коэффициент для вещества в форме шара используя эту формулу,

Где,

c_d = Коэффициент давления сопротивления для вещества в форме сферы

F_d = сила сопротивления для вещества в форме сферы, выраженная в ньютонах

A = Площадь формы в плане для вещества в форме сферы, выраженная в квадратных метрах.

ρ = плотность вещества в форме сферы, выраженная в килограммах на кубический метр.

v = Вязкость вещества в форме шара, выраженная в метрах в секунду.

Используя уравнение (1), задав значения плотности массы, скорости потока, силы сопротивления и площади, можно получить значение коэффициента сопротивления шара.

Для сферической материи площадь можно рассчитать как A = π r² ……..уравнение (2)

Уравнение (2) применимо для площади поверхности. Поскольку формула площади поверхности такова, A = 4 πr²

Формула коэффициента сопротивления сферы:

Формула коэффициента аэродинамического сопротивления приведена ниже,

Где,

F_d = сила сопротивления, выраженная в ньютонах

c_d = Коэффициент лобового сопротивления

ρ = плотность жидкого вещества, выраженная в килограммах на кубический метр.

 v = скорость потока жидкого вещества, выраженная в метрах в секунду

A = контрольная площадь для вещества определенной формы тела, выраженная в квадратных метрах.

Сопротивление давления для коэффициента материи формы сферы зависит от некоторых несколько фактов такие как размер и форма, означают геометрию тела сферы и вязкость жидкого вещества, через которое может течь вещество формы сферы.

Коэффициент лобового сопротивления сферы в зависимости от числа Рейнольдса:

Коэффициент лобового сопротивления сферы уменьшается с увеличением числа Рейнольдса, а коэффициент лобового сопротивления становится почти постоянным (C_D = 0.4) для числа Рейнольдса между 10³ и 2 × 10⁵. По мере увеличения числа Рейнольдса (Re > 2×10⁵) пограничный слой перед сферой утончается и начинает переходить в турбулентный.

Изображение – коэффициент лобового сопротивления сферы в зависимости от числа Рейнольдса;
Кредит изображения — Википедия

Когда система спроектирована так, что поток движется через жидкое вещество, это сопротивление времени лучше всего подходит для измерения системы или расчета сопротивления с помощью моделирования. Коэффициент сопротивления часто бывает полезен для возврата данных для конкретной аналитической модели.

Единственная проблема, возникающая при этом процессе, заключается в том, что одна модель не подходит для вывода всех типов течения в жидком веществе в переходной области и для обоих режимов.

Вместо конкретной практики используются измерения и смоделированные данные для расчета моделей в каждом режиме потока, а затем отслеживание пересечения моделей для расчета области перехода.

Теперь мы собираемся обсудить примеры и C_f выражение учитывается как для сопротивления давления, так и для сопротивления поверхностного трения.

• Ламинарный пример
• Бурный пример

Ламинарный пример: —

Коэффициент аэродинамического сопротивления сферы по сравнению с Рейнольдсом число для ламинарного потока можно записать как,

Коэффициент лобового сопротивления сферы в зависимости от числа Рейнольдса для ламинарный поток уравнение прекрасно сочетается с широким диапазоном чисел Рейнольдса в замкнутой системе геометрий. Коэффициент аэродинамического сопротивления сферы по сравнению с числом Рейнольдса для уравнения ламинарного потока не подходит для низкого числа Рейнольдса сопротивления, которое может быть меньше 36, особенно для несжимаемого или очень близкого к несжимаемому потоку.

В несжимаемом или очень близком к несжимаемому потоке мы можем наблюдать, что коэффициент сопротивления близок к линейной функции скорости.

Бурный пример: —

Коэффициент лобового сопротивления сферы в зависимости от числа Рейнольдса для турбулентности можно записать как

Коэффициент лобового сопротивления сферы в зависимости от числа Рейнольдса для турбулентный поток уравнение прекрасно сочетается с одним простым диапазоном чисел Рейнольдса в замкнутой системе геометрий.

Коэффициент силы сопротивления сферы:

Наиболее изучен случай коэффициента силы сопротивления для вещества тела в форме шара.

Когда тело в форме сферы в твердом состоянии взаимодействует с жидкостью, коэффициент силы сопротивления времени создается на твердом веществе в форме сферы. Коэффициент силы сопротивления сферической материи не создается никаким типом силового поля.

Часто задаваемые вопросы: —

Вопрос: —

Напишите о коэффициенте сопротивления трения кожи.

Решение: —. Коэффициент трения кожи – это физический параметр, представляющий собой безразмерное напряжение сдвига кожи. В основном он безразмерен из-за динамического давления, оказываемого на вещество набегающим потоком.

Формула коэффициента сопротивления трения кожи:

Где,

C_f = коэффициент трения кожи

T_w= Напряжение сдвига кожи, приложенное к плоскости поверхности тела

v_∞ = Скорость свободного потока для скорости тела

ρ_∞ = Скорость свободного потока для плотности тела

1/2р_∞ v²_∞ ≡ д_∞ = Динамическое давление свободного потока для тела материи

Связь с числом Рейнольдса и коэффициентом сопротивления трения кожи косвенно пропорциональна друг другу. Означает, что если число Рейнольдса увеличивается, коэффициент сопротивления трения кожи уменьшается, а если число Рейнольдса уменьшается, коэффициент сопротивления трения кожи увеличивается. +[/latex]

Где,

y = представляет расстояние от стены

u = скорость движущейся жидкости, заданная как y

K₁ = Карман Константа

Значение постоянной Кармана ниже 0.41, а постоянная Кармана является значением для переходного пограничного слоя и турбулентного пограничного слоя.

K₂= постоянная Ван Драйста

K₃= Параметр давления

р = давление

x = координата вдоль поверхности, где формируются пограничные слои

Турбулентный поток:-

Вопрос: —

Рива каждый день ездит на машине из Калькутты в Дургапур. Когда Рива ведет свою машину, в это время скорость машины составляет около 90 километров в час, а коэффициент лобового сопротивления равен 0.35. Площадь поперечного сечения автомобиля составляет 6 квадратных метров.

Теперь определите величину силы сопротивления.

Решение: — Данные данные,

Скорость автомобиля = 90 километров в час.

Коэффициент аэродинамического сопротивления автомобиля = 0.35.

Площадь поперечного сечения автомобиля = 6 кв.

Плотность жидкости автомобиля = 1.2 килограмма на кубический метр.

Все мы знаем, что скорость воздуха составляет 1.2 килограмма на кубический метр.

Теперь, применив формулу силы сопротивления,

Где,

D = сила сопротивления давления

C_d= Коэффициент сопротивления давлению

ρ = плотность

 v = скорость

 A = контрольная площадь

Д = 0.35*1.2*8100*6/2*3600

D = 2.8 Ньютона

Рива каждый день ездит на машине из Калькутты в Дургапур. Когда Рива ведет свою машину, в это время скорость машины составляет около 90 километров в час, а коэффициент лобового сопротивления равен 0.35. Площадь поперечного сечения автомобиля составляет 6 квадратных метров.

Величина силы сопротивления 2.8 ньютона

Вопрос: —

Самолет ежедневно летает из Мумбаи в Катакану. Когда самолет движется в это время, скорость самолета составляет около 750 километров в час, а коэффициент лобового сопротивления в это время равен 0. 30. Площадь поперечного сечения автомобиля составляет 115 квадратных метров.

Теперь определите величину силы сопротивления для самолета.

Решение: — Данные данные,

Скорость самолета = 750 километров в час.

Коэффициент аэродинамического сопротивления самолета = 0.30

Площадь поперечного сечения самолета = 115 квадратных метров.

Плотность жидкости самолета = 1.2 килограмма на кубический метр.

Все мы знаем, что скорость воздуха составляет 1.2 килограмма на кубический метр.

Теперь, применив формулу силы сопротивления,

Д = С_d * р * А/2

Где,

D = сила сопротивления давления

C_d = Коэффициент сопротивления давлению

ρ = плотность

 v = скорость

 A = контрольная площадь

D = 3234 Ньютона

Самолет ежедневно летает из Мумбаи в Катакану. Когда самолет движется в это время, скорость самолета составляет около 750 километров в час, а коэффициент лобового сопротивления в это время равен 0. 30. Площадь поперечного сечения автомобиля составляет 115 квадратных метров.

Сила лобового сопротивления самолета составляет 3234 ньютона.

Вопрос: —

Какая связь между сопротивлением и числом Рейнольдса?

Решение: — Связь между сопротивлением и числом Рейнольдса прямо пропорциональна друг другу. Это означает, что если сопротивление увеличивается, число Рейнольдса также увеличивается, а если сопротивление уменьшается, число Рейнольдса также уменьшается.

При увеличении числа Рейнольдса силы вязкости уменьшаются по отношению к внутренним силам, так что точка отрыва перемещается вверх по направлению к экватору.

Как рассчитать коэффициент лобового сопротивления: несколько сущностей и фактов

Сопротивление является одним из основных объектов, описанных в гидродинамике, который используется для объяснения движения твердого тела и жидкости. Сила сопротивления рассматривается как противодействующая сила в воздушной среде, пропорциональная движению тела над жидкостью.

Коэффициент сопротивления — это безразмерная величина, определяющая сопротивление, оказываемое объекту в жидкой среде, такой как воздух и вода. Коэффициент аэродинамического сопротивления зависит от формы, угла наклона и скорости потока в аэродинамике. Включая все эти условия, давайте узнаем, как рассчитать коэффициент сопротивления через этот пост.

Как рассчитать коэффициент сопротивления без учета силы сопротивления?

Коэффициенты сопротивления обычно описываются с использованием силы сопротивления. Коэффициенты сопротивления всегда зависят от площади поверхности и плотность жидкости, над которой находится объект двигается. Предположим, мы не знаем о силе сопротивления, действующей на объект, тогда как рассчитать коэффициент сопротивления?

предполагать тело движется в воздухе; на него действует сила, противодействующая движению тела. Поскольку тело находится в движении, оно имеет определенную скорость. Мы можем рассчитать коэффициент сопротивления, используя законы движения Ньютона, не используя силу сопротивления, используя конечную скорость.

Кредиты изображения: Изображение предоставлено Марселькесслер из Pixabay 

Суммарная сила, действующая на тело над жидкостью, определяется выражением

F=мг–F_D

Где F_D сила сопротивления;

от Второй закон движения Ньютона, результирующая сила равна F = ma

Следовательно, сила сопротивления может быть приравнена к чистой силе как

ма=мг–F_D

Но ма=0; поэтому F_D= мг

Предположим, что тело имеет плотность ρ, площадь поперечного сечения A и скорость тела v. Сила сопротивления, противодействующая движению, определяется как

F_D=1/2 ρ С_DV^2A

Где F_D сила сопротивления, C_D это коэффициент лобового сопротивления.

Но сила сопротивления равна весу тела в жидкости. Следовательно, приведенное выше уравнение можно изменить как

мг= 1/2 ρ С_DV^2A

Переставляя члены, мы получаем коэффициент лобового сопротивления как

C_D= 2мг/ρv^2A

Как рассчитать коэффициент аэродинамического сопротивления цилиндра?

Силу сопротивления цилиндра можно определить, разложив площадь цилиндра.

Рассмотрим цилиндрическое тело, плавающее в жидкости. Тело испытывает некоторое сопротивление, которое возражает против движения цилиндра.

Коэффициент аэродинамического сопротивления цилиндра

Коэффициент лобового сопротивления обычно определяется по формуле

CD = 2F_D/ ρв^2A

Где; ρ — плотность цилиндра, FD — сила сопротивления, v — скорость цилиндра, движущегося в жидкости, A — площадь цилиндра.

Площадь цилиндра определяется выражением

А=2πр+2πр²

А=2πr(ч+г)

Подставив значение площади цилиндра в приведенное выше уравнение коэффициента лобового сопротивления, получим

C_D= 2F_D/ ρв^2A(2 πr(h+r))

C_D= ρv²(πr(ч+r)

Как рассчитать коэффициент сопротивления шара?

Коэффициент сопротивления сферы включает в себя тот же процесс, что и коэффициент сопротивления цилиндра. Вычислив площадь сферы, можно найти сферу с коэффициентом лобового сопротивления как

Площадь сферы определяется уравнением

А = 4πr²

Коэффициент аэродинамического сопротивления определяется выражением

C_D= 2F_D/ρv^2A

Подставляя площадь сферы в приведенное выше уравнение, мы получаем

C_D= 2F_D/ρv²(4 πr²)

C_D= Ф_D/ρv²(2πr²)

C_D= Ф_D/2ρv²(πr²)

Как рассчитать коэффициент аэродинамического сопротивления парашюта?

Сила сопротивления в парашюте действует противоположно сила гравитации; следовательно, парашютист замедляется при падении с парашюта.

Когда парашютист ныряет с парашютом, его скорость определяется гравитационным притяжением. При раскрытии парашюта будет увеличиваться площадь поверхности, а значит будет больше воздуха и скорость автоматически замедляется из-за сопротивление воздуха.

Свободно падающий парашют с описанием расчета коэффициента лобового сопротивления.

Сначала рассмотрите свободное падение парашюта; скорость водолаза считается a=-g, так как из-за сопротивления воздуха парашют медленно движется вверх. Но результирующая сила действует вниз, что намного больше, чем сила сопротивления.

Величина сила сопротивления из-за конечной скорости дан кем-то

|F_D|=С_D v

Где компакт-диск коэффициент трения, v — конечная скорость.

Суммарная действующая сила определяется выражением

∑F=F_D–мг=0

F_D= мг

C_D v_{терминал} = мг

C_D=мг/об._{терминал}

Как рассчитать коэффициент лобового сопротивления в cfd?

Для точной оценки коэффициента сопротивления широко используется вычислительная гидродинамика (CFD). Существует различное программное обеспечение, которое поможет вам рассчитать коэффициент аэродинамического сопротивления, используя предоставленные вам данные.

Тяжелые объекты, такие как транспортные средства, проектируются с помощью аэродинамики с использованием анализа CFD. Пример коэффициент трения Расчет с использованием моделирования Autodesk показан ниже:

Для получения точных результатов следуйте приведенным ниже методам.

• Для расчета необходимо использовать большую воздушную область, чтобы избежать искусственного ускорения из-за воздуха.
• Необходимо создать мелкую сетку объекта.
• Запустите расчет для нескольких итераций, чтобы получить точный результат.
• Всегда используйте площадь поперечного сечения объекта, которая уже определена.

Когда вы открываете программное обеспечение, необходимо выполнить следующие шаги

• Выберите соответствующий инструмент стены
• Внешняя поверхность объекта должна быть выбрана
• Появится флажок, затем выберите Ньютон и нажмите «Рассчитать для вывода».
• Выберите «всего FX»; направление движения объекта, то поставить формулу.

C_D=2F_D/ρv^2A

Как рассчитать коэффициент лобового сопротивления по числу Рейнольдса?

Течение объекта в жидкости, тормозящее сопротивление, рассчитывается по эмпирической формуле с использованием числа Рейнольдса.

Число Рейнольдса для объекта плотности D и площадь поперечного сечения влияют на коэффициент лобового сопротивления. Коэффициент аэродинамического сопротивления уменьшается по мере Число Рейнольдса увеличивается.

Число Рейнольдса определяется как

Re={ρvD/µ}

Где ρ — плотность объекта, D — диаметр, μ — вязкость, v — скорость.

Стокс дал формулу для силы сопротивления как функции некоторого постоянного числа как

F_D=6πμRv

Для большего значения Re, C_D уменьшается по мере того, как скорость изменяется в терминах квадратного значения. 2/µD}, называемое числом Бежана

Как найти нулевой коэффициент подъемной силы?

Безразмерный параметр, характеризующий силу сопротивления при нулевой подъемной силе самолета с учетом его размеров, скорости и высоты, называется коэффициентом сопротивления при нулевой подъемной силе.

Как правило, коэффициент сопротивления при нулевой подъемной силе отражает паразитное сопротивление, описывающее обтекаемость самолета.

Математически коэффициент сопротивления при нулевой подъемной силе определяется как

C_{D, 0} = C_D-С_{D, I}

C_D — коэффициент лобового сопротивления, а C_{Д, я} — коэффициент индуктивного сопротивления.

Полное сопротивление находится по формуле.

C_D={550ηP/(1/2)ρ₀Σс (1.47 В)³

Где η — КПД тяги, а P — мощность двигателя, ρ₀ — плотность воздуха на уровне моря, σ — плотность атмосферы, s — площадь крыла, v — скорость.

Упрощая вышеприведенное уравнение, получаем

C_D= 1.456 * 10⁵(η P/Σsv³)

Индуцированное сопротивление определяется выражением

C_D,_i= {С_L²/ π ARɛ}

Где C_L — коэффициент подъемной силы, AR — удлинение, ε — эффективность.

Подставляя значение коэффициента подъемной силы

C_D,_i={4.822*10⁴/ARɛΣ^2v4}

Подставляя и вычисляя, получаем коэффициент сопротивления при нулевой подъемной силе

Как найти минимальный коэффициент лобового сопротивления?

Симметричный обтекаемый аэродинамический профиль обеспечивает минимальный коэффициент лобового сопротивления.

Минимальное сопротивление можно определить как

C_D=C_D0+кС_L²

Где C_D0 сопротивление профиля и C_L — подъемное сопротивление, а k — коэффициент подъемной силы.

Для минимального коэффициента лобового сопротивления

dC_DdC_L=0

Учитывая, что самолет находится в прямолинейном и горизонтальном полете, минимальное сопротивление должно иметь максимальное аэродинамическое качество, т. е.

{d²C_L/Округ Колумбия_D²}<0

Разделив первое уравнение на C_L,

Мы получаем

C_LC_D=C_D/C_L+кС_L

Решенные проблемы

Найдите коэффициент лобового сопротивления лодки, плавающей на воде плотностью 1.2 кг/м.³ а площадь поперечного сечения 7м² и движется со скоростью 23 м/с и массой лодки 66 кг.

Решение:

Дано – плотность ρ=1.2 кг/м³

Площадь поперечного сечения A=7м²

Масса лодки m=66кг.

Скорость лодки v=23м/с

Ускорение свободного падения g = 9.8 м/с.²

Коэффициент лобового сопротивления определяется выражением

C_D={2мг/ρv²A}

C_D={2(66*9. 8)}{1.2*23²*7}

C_D={1293.6/4443.6}

C_D= 0.291

В жидкости движется тело, площадь увлажнения которого равна 3 м, а площадь фронта 33 м. Число Рейнольдса длины пути равно 0.19, а число Бежана — 0.96. Вычислите коэффициент сопротивления данного тела.

Решение:

Коэффициент аэродинамического сопротивления C_D для заданного числа Рейнольдса определяется выражением

C_D= 2 {А_w/A_f}{Be/ReL²}

C_D=2{3/36}{0.96/0.19²}

C_D= 4.43.

Сферический предмет радиусом 2 м брошен в воздух, сила сопротивления которого равна 123 Н, а плотность равна 1.34 кг/м.³, а скорость объекта в воздухе 34 м/с. Как рассчитать коэффициент аэродинамического сопротивления по предоставленным данным?

Решение:

Дано – радиус объекта r=2м

Сила сопротивления, действующая на объект F_D= 123N

Скорость объекта v=34 м/с

Плотность ρ=1. 34 кг/м³

Площадь сферы A=4πr²

A = 50.24 м²

Коэффициент аэродинамического сопротивления определяется выражением

C_D={2F_D/ ρ v²A}

C_D={2(123)/1.34*34²*50.24}

C_D= 3.16 × 10^-3

Уравнение сопротивления

Перетаскивание зависит от плотность воздуха, квадрат скорости, вязкость и сжимаемость воздуха, размер и форма тело и склонность тела к поток. В целом зависимость от формы тела, наклона, воздуха вязкость и сжимаемость очень сложны. Один из способов справиться со сложными зависимостями — охарактеризовать зависимость от одной переменной. Для перетаскивания эта переменная называется коэффициент аэродинамического сопротивления, обозначенный 92 Для данного воздуха условиях, форме и наклоне объекта, мы должны определить значение для Cd для определения сопротивления. Определение стоимости коэффициент лобового сопротивления сложнее, чем определение коэффициент подъемной силы из-за многократного источники сопротивления. Приведенный выше коэффициент лобового сопротивления включает форму компоненты сопротивления, сопротивления поверхностного трения и волнового сопротивления. Коэффициенты аэродинамического сопротивления почти всегда определяется опытным путем с помощью аэродинамическая труба. Обратите внимание, что площадь (A), заданная в уравнении сопротивления, представлена ​​как опорная область . Перетаскивание напрямую зависит от размера тела. Поскольку мы имеем дело с аэродинамическими сил зависимость может быть охарактеризована некоторой площадью. Но какой район выбираем? Если мы думаем, что сопротивление вызвано трения между воздухом и телом, логичным выбором было бы общая площадь поверхности тела. Если мы думаем о перетаскивании как о сопротивление потоку, более логичным выбором будет лобовое участок тела, перпендикулярный направлению потока. А также наконец, если мы хотим сравнить с коэффициентом подъемной силы, мы должны используйте ту же площадь крыла, которая использовалась для получения коэффициента подъемной силы. Поскольку Коэффициент лобового сопротивления обычно определяют экспериментально путем измерения перетащите и область, а затем выполните деление, чтобы получить коэффициент, мы можем использовать любая область которую можно легко измерено. Если мы выберем площадь крыла, а не поперечное сечение площадь, вычисленный коэффициент будет иметь другое значение. Но сопротивление одинаково, а коэффициенты связаны отношением области. На практике коэффициенты аэродинамического сопротивления сообщаются на основе широкий выбор площадей объектов. В отчете инженер-испытатель должен укажите используемую площадь; при использовании данных читателю, возможно, придется преобразовать коэффициент лобового сопротивления, используя соотношение площадей. В приведенном выше уравнении плотность обозначается как греческая буква «ро». Мы не используем «d» для плотности так как «d» часто используется указать расстояние. Сочетание термины «плотность, умноженная на квадрат скорости, деленный на два» называется динамическое давление и появляется у Бернулли уравнение давления. Экскурсии с гидом Ракетная аэродинамика: Вязкостная аэродинамика: Деятельность: Связанные сайты: Rocket Index Rocket Home Руководство для начинающих Home

5.2 Силы сопротивления – College Physics

Глава 5 Дополнительные применения законов Ньютона: трение, сопротивление и упругость

Резюме

• Выразите математически силу сопротивления.
• Обсудите применение силы сопротивления.
• Задайте конечную скорость.
• Определить конечную скорость при заданной массе.

 

Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (будь то газ или жидкость). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. Чем быстрее вы двигаете рукой, тем труднее двигаться. Вы чувствуете меньшую силу сопротивления, когда наклоняете руку так, чтобы только сторона проходила через воздух — вы уменьшили площадь своей руки, обращенную в направлении движения. Как и трение, сила сопротивления всегда противодействует движению объекта. В отличие от простого трения, сила сопротивления пропорциональна некоторой функции скорости объекта в этой жидкости. Эта функциональность сложна и зависит от формы объекта, его размера, его скорости и жидкости, в которой он находится. Для большинства крупных объектов, таких как велосипедисты, автомобили и бейсбольные мячи, движущихся не слишком медленно, величина силы сопротивления [ латекс] {F_{\text{D}}}[/латекс] пропорциональна квадрату скорости объекта.

2}}.[/latex] Принимая во внимание другие факторы, это отношение становится равным 9.2},[/latex], где [latex]{b}[/latex] — константа, эквивалентная [latex]{0,5C\rho{A}}.[/latex] Мы установили показатель степени для этих уравнений равным 2. потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим через несколько страниц гидродинамики, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени равен 1,

.

СИЛА СОПРОТИВЛЕНИЯ

Установлено, что сила сопротивления [латекс]{F_{\text{D}}}[/латекс] пропорциональна квадрату скорости объекта. Математически 92,}[/latex]

, где [latex]{C}[/latex] — коэффициент сопротивления, [latex] {A}[/latex] — площадь объекта, обращенная к жидкости, а [latex]{ \rho}[/latex] — плотность жидкости.

 

Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время своих гонок. (См. рис. 1). «Аэродинамическая» форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.

Рисунок 1. От гоночных автомобилей до гонщиков бобслея аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости. Они имеют форму пули с коническими плавниками. (кредит: армия США, Wikimedia Commons)

Значение коэффициента аэродинамического сопротивления, [латекс]{C},[/латекс] определяется опытным путем, обычно с использованием аэродинамической трубы. (См. рис. 2).

Рис. 2. Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)

Коэффициент лобового сопротивления может зависеть от скорости, но мы будем считать, что здесь он является константой. В таблице 2 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На скоростях шоссе более 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). По этой причине в течение 19Во время нефтяного кризиса 70-х годов в США максимальная скорость на шоссе была установлена ​​​​на уровне около 90 км / ч (55 миль / ч).

[латекс]\текст{Объект}[/латекс]	[латекс]\текст{С}[/латекс]
Аэродинамический профиль	0,05
Тойота Камри	0,28
Форд Фокус	0,32
Хонда Сивик	0,36
Феррари Тестаросса	0,37
Пикап Dodge Ram	0,43
Сфера	0,45
Внедорожник Hummer h3	0,64
Парашютист (ногами вперед)	0,70
Велосипед	0,90
Парашютист (горизонтальный)	1,0
Круглая плоская пластина	1,12
Таблица 2. Значения коэффициента сопротивления Типичные значения коэффициента сопротивления [латекс]{C}[/латекс].

В мире спорта ведутся серьезные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (см. рис. 3). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила.

Рисунок 3. Костюмы для тела , такие как этот костюм-гонщик LZR, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньшее сопротивление. (Фото: НАСА/Кэти Барнсторфф)

Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении воздействия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорение отсутствует, как указано во втором законе Ньютона.

В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своего конечная скорость ([латекс]{вт}[/латекс]). Поскольку [латекс]{F_{\text{D}}}[/латекс] пропорционален скорости, более тяжелый парашютист должен двигаться быстрее, чтобы [латекс]{F_{\текст{D}}}[/латекс] был равен его вес. Давайте посмотрим, как это работает более количественно.

На предельной скорости,

[латекс] {F _ {\ text {net}} = мг-F _ {\ text {D}} = ma = 0.} [/ латекс]

Таким образом,

[латекс] {мг = F _ {\ текст {D}}.} [/латекс]

Используя уравнение для силы сопротивления, мы имеем

92)}}}[/латекс]

[латекс]{=98\текст{ м/с}}[/латекс]

[латекс]{=350\текст{км/ч}}.[/латекс]

Это означает, что парашютист массой 75 кг достигает максимальной конечной скорости около 350 км/ч, путешествуя в положении согнувшись (головой вперед), сводя к минимуму площадь и сопротивление. В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. 2}[/латекс] в зависимости от массы. Какая из этих зависимостей более линейна? Какой вывод вы можете сделать из этих графиков? 92)}}}[/latex]

[latex]{=44\text{ м/с}}.[/latex]

Обсуждение

Этот результат согласуется со значением для [latex]{v_ {\text{t}}}[/latex], упомянутый ранее. 75-килограммовый парашютист, идущий ногами вперед, имел [латекс]{v=98\text{ м/с}}.[/латекс] Он весил меньше, но имел меньшую лобную площадь и, следовательно, меньшее сопротивление воздуха.

Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, но белка достигает.

Следующая интересная цитата о размере животных и конечной скорости взята из эссе 1928 года британского биолога Дж. Б.С. Холдейна под названием «О том, чтобы быть подходящего размера».

Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз превышает движущую силу.

Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Это отношение задается законом Стокса , который гласит, что

[латекс] {F _ {\ text {s}} = 6 \ pi {r} \ eta {v}}, [/ латекс]

, где [латекс]{r}[/латекс] — радиус объекта, [латекс]{\эта}[/латекс] — вязкость жидкости, а [латекс]{v}[/латекс] — скорость объекта.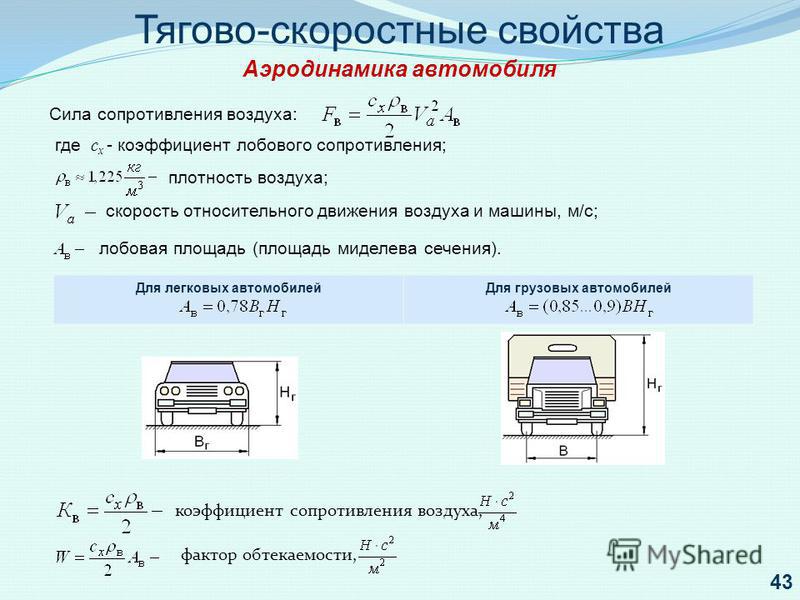

ЗАКОН СТОКА

[латекс] {F_{\text{s}}=6\pi{r}\eta{v}},[/latex]

, где [латекс]{r}[/латекс] радиус объекта, [latex]{\eta}[/latex] — вязкость жидкости, а [latex]{v}[/latex] — скорость объекта.

Хорошими примерами этого закона являются микроорганизмы, пыльца и частицы пыли. Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером примерно [латекс]{1\:\mu}[/латекс] ) может быть примерно [латекс]{2\:\мю\текст{/с}}.[/латекс] Чтобы двигаться со С большей скоростью многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие маленькими двигателями, встроенными в клетку. Отложения в озере могут двигаться с большей конечной скоростью (около [latex]{5\:\mu\text{/s}}[/latex] ), поэтому может пройти несколько дней, прежде чем они достигнут дна озера после отложения. на поверхности.

Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, формируя обтекаемый рисунок (см. рис. 4). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию 9.0089 .

Рисунок 4. Гуси летят V-образным строем во время своих длительных миграционных путешествий. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (Фото: Julo, Wikimedia Commons)

ЭКСПЕРИМЕНТ ГАЛИЛЕЯ

Говорят, что Галилей сбросил с Пизанской башни два объекта разной массы. Он измерил, сколько времени потребовалось каждому, чтобы достичь земли. Поскольку секундомеры были недоступны, как, по-вашему, он измерял время их падения? Если бы объекты были одного размера, но разной массы, что, по вашему мнению, он должен был бы наблюдать? Был бы этот результат другим, если бы это было сделано на Луне?

ИССЛЕДОВАНИЯ PHET: МАССЫ И ПРУЖИНЫ

Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины.

Рис. 5. Массы и пружины

• Силы сопротивления, действующие на объект, движущийся в жидкости, противодействуют движению. Для более крупных объектов (таких как бейсбольный мяч), движущихся со скоростью [латекс]{v}[/латекс] в воздухе, сила сопротивления определяется выражением 92},[/латекс]

  , где [латекс]{C}[/латекс] — коэффициент сопротивления (типичные значения приведены в таблице 2), [латекс] {А}[/латекс] — площадь объекта, обращенная к жидкости, а [латекс] {\rho}[/latex] — плотность жидкости.