Лобовое сопротивление (аэродинамика) | это… Что такое Лобовое сопротивление (аэродинамика)?

Четыре силы, действующие на самолёт

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивления складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Поток и форма препятствия	Профильное сопротивление	Сопротивление обшивки
	0%	100%
	~10%	~90%
	~90%	~10%
	100%	0%

Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота). Чёрный объект не испытывает никакого сопротивления и движется по параболе, на голубой объект действует Закон Стокса, на зеленый объект — закон вязкости Ньютона

Содержание 1 Сопротивление при нулевой подъёмной силе 2 Индуктивное сопротивление 3 Суммарное сопротивление 4 См. также 5 Ссылки

Сопротивление при нулевой подъёмной силе

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления.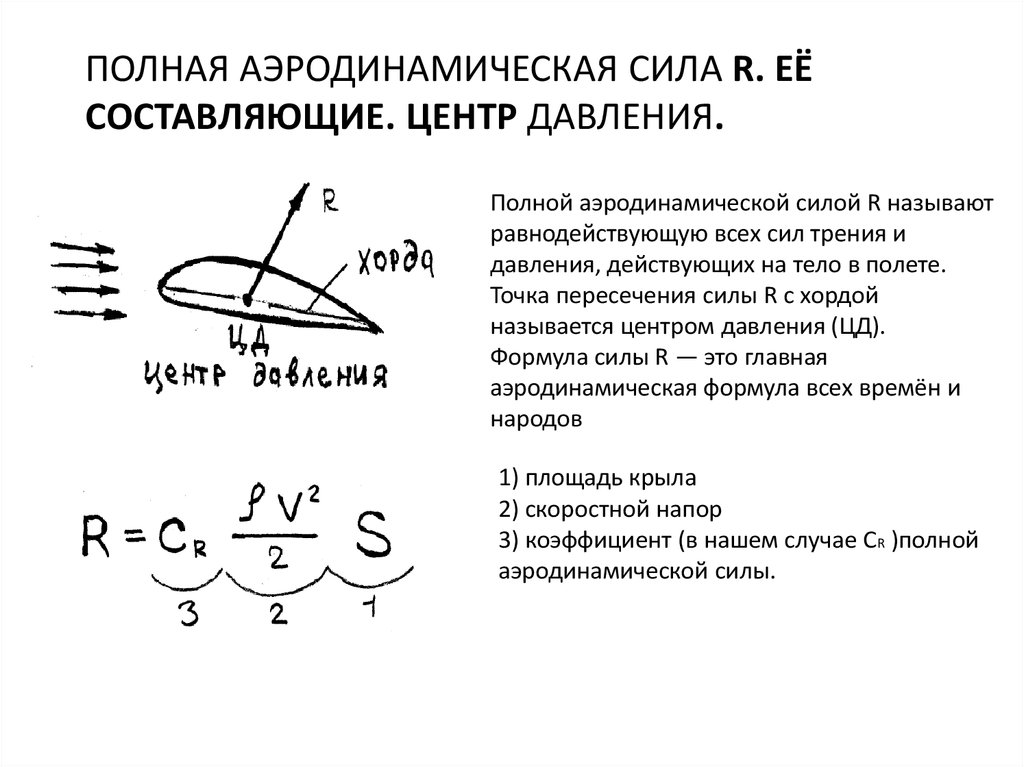

Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

C_x0 — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

• в простейшем случае (шар) — площадь поперечного сечения;
• для крыльев и оперения — площадь крыла/оперения в плане;
• для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
• для продолговатых тел вращения ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V^2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости.

Индуктивное сопротивление

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение во-первых сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления.

На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы, но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху. При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ, плотности среды ρ и квадрату скорости V:

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

X = X₀ + X_i

Так как сопротивление при нулевой подъёмной силе X₀ пропорционально квадрату скорости, а индуктивное 

X_i — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости, X₀ растёт, а X_i — падает, и график зависимости суммарного сопротивления X от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых X₀ и X_i, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно-пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит и расход топлива) становится минимальной — это скорость

наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

См. также

• Эффект Бартини

Ссылки

• Аэродинамическое сопротивление — статья из Большой советской энциклопедии
• Аэродинамическое сопротивление — статья из Физической энциклопедии
• Юрьев Б. Н. Экспериментальная аэродинамика. Часть II Индуктивное сопротивление, НКОП СССР, 1938, 275 с.

Силы, действующие на самолёт

Подъёмная сила • Вес • Тяга • Лобовое сопротивление

 

Коэффициент аэродинамического сопротивления во Flow simulation 2016

Вступление.

Добрый день, дорогие читатели. В данном посте я хочу рассказать, как посредствам внутреннего анализа во Flow simulation выполнить внешний анализ детали или конструкции на определения коэффициента аэродинамического сопротивления и результирующей силы. Так же рассмотреть создание локальной сетки и задание целей ‘цель-выражение’ для упрощения и автоматизации расчетов. Приведу основные понятия по коэффициенту аэродинамического сопротивления.

Все эти сведения помогут быстро и грамотно спроектировать бедующее изделия и в дальнейшем распечатать его для практического использования.

Матчасть.

Коэффициент аэродинамического сопротивления (далее КАС) определяется экспериментально при испытаниях в аэродинамической трубе или испытаниях при движении накатом. Определение КАС приходит с формулой 1

формула 1

КАС разных форм колеблется в широком диапазоне. Рисунок 1 показывает эти коэффициенты для ряда форм. В каждом случае предполагается, что воздух, набегающий на тело, не имеет боковой компоненты (то есть движется прямо вдоль продольной оси транспортного средства). Обратите внимание, что простая плоская пластина имеет коэффициент аэродинамического сопротивления 1.95. Этот коэффициент означает, что сила лобового сопротивления в 1.95 раза больше, чем динамическое давление, действующее на площадь пластины. Крайне большое сопротивление, создаваемое пластиной, связано с тем, что воздух, растекающийся вокруг пластины, создаёт область отрыва гораздо большую, чем сама пластина.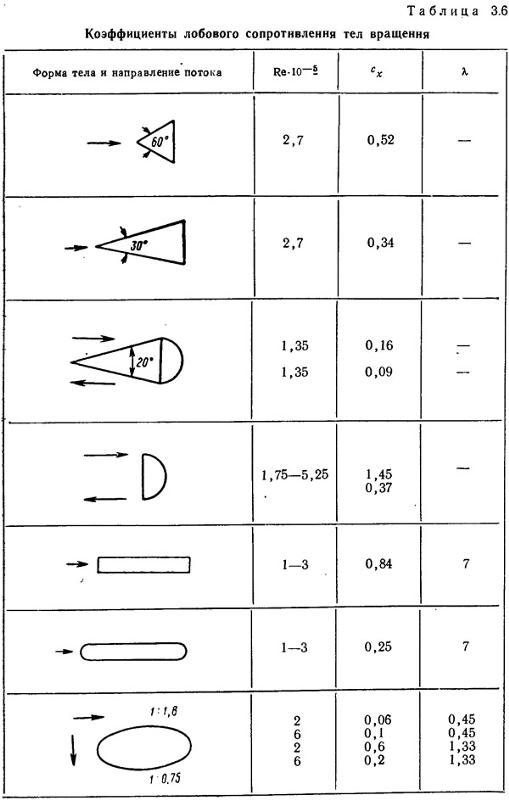

Рисунок 1.

В жизни в дополнение к составляющей ветра, вытекающей из скорости движения автомобиля, учитывают скрость находящего ветра на автомобиль. И того для определения скорости потока верно следующее утверждение V=Vавто+Vветра.

Если находящий ветер является попутным то скорость вычитается.

Коэффициент аэродинамического сопротивления нужен для определения аэродинамического сопротивления, но в данной статье будет рассматриваться только сам коэффициент.

Исходные данные.

Расчет выполнялся в Solidworks 2016, модуль Flow simulation (далее FS). В качестве исходных данных были взяты следующие параметры: скорость вытекающая из скорости движения автомобиля V=40 м/с, температура окружающей среды плюс 20 градусов Цельсия, плотность воздуха 1,204 кг/м3. Геометрическая модель автомобиля представлена упрощенно (см. рисунок 2).

Рисунок 2.

Шаги задания начальных и граничных условий во Flow simulation.

Процесс добавления модуля FS и общий принцип формирования задания на расчет описан в этой статье, я же опишу характерные особенности для внешнего анализа посредствам внутреннего.

1.На первом шаге добавляем модель в рабочее пространство.

Рисунок 2.

2. Далее моделируем аэродинамическую камеру прямоугольного сечения. Главная особенность при моделирование это отсутствие торцов, иначе мы не сможем задать граничные условия. Модель автомобиля должна находится в центре. Ширина трубы должна соответствовать 1,5* ширины модели в обе стороны, длина трубы 1,5*длины модели, от задней части модели и 2*длины автомобиля от бампера, высота трубы 1,5*высоты машины от плоскости на которой стоит машина.

Рисунок 3.

3. Входим в модуль FS. Задаём граничные условия на первой грани входной поток.

Рисунок 4.

Выбираем тип: расход/скорость->скорость на входе. Задаём нашу скорость. Выбираем параллельную грань к передней части авто. Нажимаем галочку.

Рисунок 5.

Задаём граничное условие на выходе. Выбираем тип: давление, всё оставляем по умолчанию. Жмём галку.

Итак, граничные условия заданы переходим к заданию на расчёт.

4. Нажимаем на мастер проекта и следуем инструкции по рисункам ниже.

Рисунок 6.

Рисунок 7.

Рисунок 8.

Рисунок 9.

Рисунок 10.

Рисунок 11.

В пункте завершение оставляем всё без изменений. Нажимаем завершить.

5. На этом шаге займёмся управлением и созданием локальной сетки. Нажимаем на дереве элементов FS на пункт: сетка, правой кнопкой мыши и выбираем: добавить локальную сетку.

Рисунок 12.

Рисунок 13.

Здесь можно указать параметры и область локальной сетки, для сложных моделей так же задаётся угол кривизны и минимальный размер элемента. Минимальный размер задаётся в графе ‘закрытие узкие щели’. Данная функция существенно сокращает время расчета и увеличивает точность полученных данных. В зависимости от того, насколько точно вы хотите получить результаты, выставляется параметр дробление сетки. Для внутреннего анализа вполне подходят стандартные настройки. Далее будет показана визуализация сетки на поверхности.

6.Перед тем как запустить расчет нужно задать цели расчета. Цели задаются в дереве FS цели. В начале задаём глобальные цели, выбираем силы по каждой компоненте.

Рисунок 14.

После нам нужно задать ‘цели-выражения’. Для этого щелкаем правой кнопкой мыши в дереве FS на цели и выбираем ‘цель выражение’. Для начала зададим уравнения для результирующей силы .

Рисунок 15.

Что бы компанента по силе использовалась в выражение нужно щёлкнуть на неё левой кнопкой мыши , ссылка на компоненту появится в формуле. Здесь вводим формулу 2. Нажимаем на галку.

Формула 2.

Создаём вторую ‘цель-выражение’, записываем туда формулу 1.

Рисунок 16.

КАС расчтывается для лобового стекла. В данной модели лобовое стекло это наклонная грань, грань наклонена на 155 градусов, поэтому сила по X умножается на sin(155*(пи/180)). Нужно помнить, что расчет ведётся по системе си и соответственно площадь наклонной грани должна измеряться в метрах квадратных.

7. Теперь можно приступить к расчету, запускаем расчет.

Рисунок 17.

При запуске расчета программа предоставляет выбор на чем производить расчет, мы можем выбрать количество ядер участвующие в расчете и рабочие станции.

Рисунок 18.

Так как задача не сложная расчет проходит меньше чем за минуту, поэтому мы нажмём на паузу после его запуска.

Рисунок 19.

Теперь нажимаем на кнопку ‘вставить график’, выбираем наши цели выражения.

Рисунок 20.

На графике будут показаны значения для наших выражений для каждой итерации.

Для наблюдения происходящего процесса во время расчета можно использовать ‘предварительный просмотр’. При включении предварительного просмотра время нашего расчета увеличивается, а смысла от него мало, поэтому я не советую включать данную опцию, но покажу как это выглядит.

Рисунок 21.

Рисунок 22.

То что эпюра перевёрнута нет ни чего страшного, это зависит от ориентации модели.

Расчёт заканчивается когда все цели сошлись.

Рисунок 23.

Результаты должны загрузиться автоматически, если этого не произошло догрузите вручную: инструменты->FS->результаты->загрузить из файла

8. После расчета можно посмотреть сетку на модели.

Рисунок 24.

Рисунок 25.

Выбираем грани где хотим видеть сетку.

Рисунок 26.

Такая сетка нам подходим, одна ячейка не больше самого маленького элемента в модели.

9. Теперь мы можем визуализировать полученные результаты.

Рисунок 27.

Рисунок 28.

Рисунок 29.

Мы можем наглядно увидеть и оценить правильность результатов. Под правильностью я подразумеваю, что бы они соответствовали действительным физическим процессам.

10. На красивых картинках дело не заканчивается. Для нас важно знать числовые параметры и уметь их извлекать из расчета. Ниже рассмотрено как результаты импортировать в экс ель.

Рисунок 30.

Рисунок 31.

Рисунок 32.

Эти данные можно использовать для проведение исследования зависимости угла наклона лобового стекла и величины КАС. Все результаты расчета во FS можно импортировать в другие расчетные комплексы и использовать уже в качестве входных данных, расчетов на прочность и т.д.

На этом можно закончить статью, если будут пожелания рассмотреть какой либо еще анализ или по глубже капнуть в аэродинамику, обязательно исполню.

Модель для скачивания P.S. занимаюсь расчетами на прочность.

Сил сопротивления | Физика

Цели обучения

К концу этого раздела вы сможете:

• Выразить математически силу сопротивления.
• Обсудите применение силы сопротивления.
• Определить конечную скорость.
• Определить конечную скорость данной массы.

Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. Чем быстрее вы двигаете рукой, тем труднее двигаться. 2\\[/latex], где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости. (Напомним, что плотность — это масса на единицу объема.) Это уравнение также можно записать в более обобщенном виде: . Мы установили показатель степени n для этих уравнений равным 2, потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим через несколько страниц гидродинамики, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени 92\\[/latex],

, где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости.

Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время своих гонок. (См. рис. 1). «Аэродинамическая» форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.

Рис. 1. От гоночных автомобилей до бобслеистов аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости. Они имеют форму пули с коническими плавниками. (кредит: армия США, Wikimedia Commons)

Значение коэффициента аэродинамического сопротивления, C , определяется опытным путем, обычно с использованием аэродинамической трубы. (См. рис. 2).

Рис. 2. Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)

Коэффициент лобового сопротивления может зависеть от скорости, но мы будем считать, что здесь он является константой. В таблице 1 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На скоростях шоссе более 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). По этой причине в течение 19Во время нефтяного кризиса 70-х годов в США максимальная скорость на шоссе была установлена ​​​​на уровне около 90 км / ч (55 миль / ч).

Таблица 1. Значения коэффициента лобового сопротивления Типичные значения коэффициента лобового сопротивления C .
ОБЪЕКТ	С
Аэродинамический профиль	0,05
Тойота Камри	0,28
Форд Фокус	0,32
Хонда Сивик	0,36
Феррари Тестаросса	0,37
Пикап Dodge Ram	0,43
Сфера	0,45
Внедорожник Hummer h3	0,64
Парашютист (ноги вперед)	0,70
Велосипед	0,90
Парашютист (горизонтальный)	1,0
Круглая плоская пластина	1,12

Рисунок 3. Боди, такие как этот LZR Racer Suit, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньшее сопротивление. (Фото: НАСА/Кэти Барнсторфф)

В мире спорта ведутся серьезные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (см. рис. 3). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила.

Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении воздействия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорение отсутствует, как указано во втором законе Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своего 9{2}\right)}}\\ & =& \text{98 м/с}\\ & =& \text{350 км/ч}\text{.}\end{массив}\\[/latex]

Это означает, что парашютист массой 75 кг достигает максимальной конечной скорости около 350 км/ч, путешествуя в положении согнувшись (головой вперед), сводя к минимуму площадь и сопротивление. В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.

Возьми домой эксперимент

В этом интересном занятии исследуется влияние веса на конечную скорость. Соберите вместе несколько вложенных фильтров для кофе. Оставив их в исходной форме, измерьте время, за которое один, два, три, четыре и пять вложенных фильтров упадут на пол с одинаковой высоты (примерно 2 м). (Обратите внимание, что из-за того, что фильтры вложены друг в друга, сопротивление постоянно, а изменяется только масса.) Они довольно быстро достигают конечной скорости, поэтому найдите эту скорость как функцию массы. Постройте конечную скорость против против массы. Также постройте v ² в зависимости от массы. Какая из этих зависимостей более линейна? Какой вывод вы можете сделать из этих графиков?

Пример 1. A Конечная скорость

Найдите конечную скорость парашютиста массой 85 кг, падающего с распростертыми крыльями. 2\\[/latex].

Таким образом, конечная скорость v _t может быть записана как [латекс]v_{\text{t}}\sqrt{\frac{2mg}{\rho{CA}}}\\[/latex].

Решение

Все величины известны, кроме площади проекции человека. Это взрослый (82 кг) падающий распростертый орел. Мы можем оценить фронтальную площадь как A = (2 м)(0,35 м) = 0,70 м ² .

Используя наше уравнение для v , мы находим, что

[латекс]\begin{array}{lll}{v}_{\text{t}}& =& \sqrt{\frac{2\left( \текст{85}\текст{кг}\справа)\слева(9{2}\right)}}\\ & =& \text{44 м/с.}\end{массив}\\[/latex]

Обсуждение

Этот результат согласуется со значением для v _т упомянутый ранее. Парашютист весом 75 кг, идущий ногами вперед, имел v = 98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха.

Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, но белка достигает.

Следующая интересная цитата о размерах животных и конечной скорости взята из эссе 1928 года британского биолога Дж.Б.С. Холдейна под названием «О том, чтобы быть подходящего размера».

Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз превышает движущую силу.

Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Это соотношение определяется законом Стокса , который гласит, что F ​​ _s = 6 πrηv , где r — радиус объекта, η — вязкость жидкости — скорость объекта.

Закон Стоукса

F ​​ _S = 6 πrηV , где R является радиусом объекта, η является вязкостью гриппа, а V — это Velocity объекта.

Рис. 4. Гуси летят V-образным строем во время длительных миграционных перемещений. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (кредит: Julo, Wikimedia Commons)

Хорошими примерами этого закона являются микроорганизмы, пыльца и частицы пыли. Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) может составлять около 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку. Отложения в озере могут двигаться с большей конечной скоростью (около 5 мкм/с), поэтому может потребоваться несколько дней, чтобы достичь дна озера после отложения на поверхности.

Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, формируя обтекаемый рисунок (см.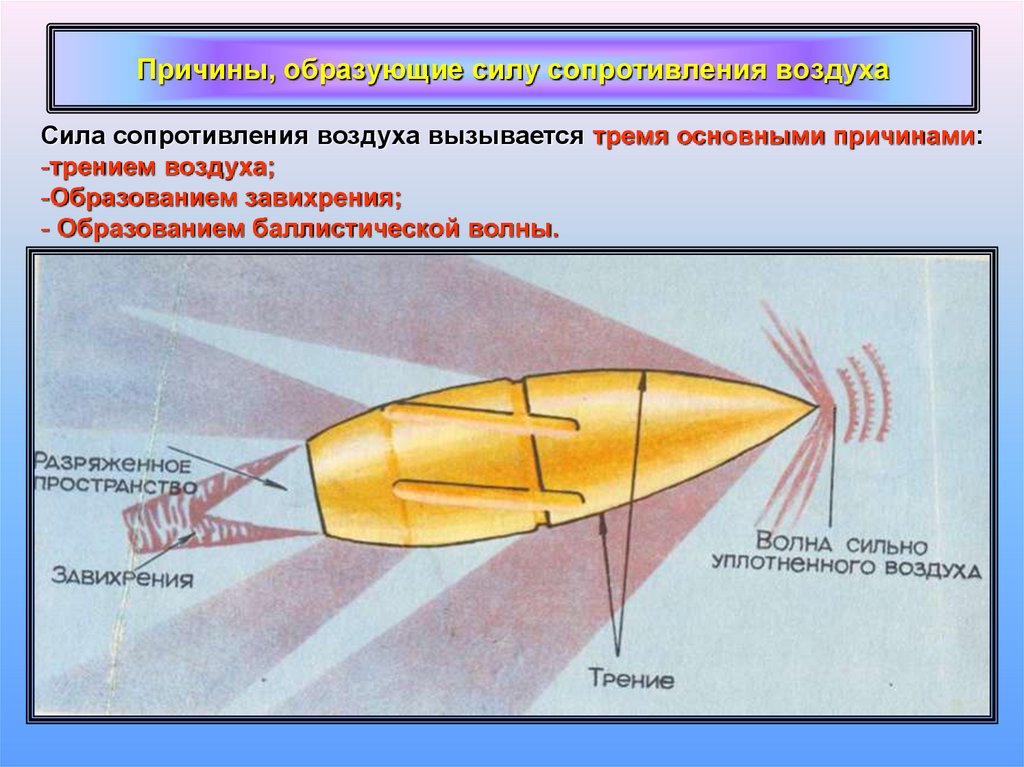 рис. 4). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию.

Эксперимент Галилея

Говорят, что Галилей сбросил с Пизанской башни два объекта разной массы. Он измерил, сколько времени потребовалось каждому, чтобы достичь земли. Поскольку секундомеры были недоступны, как, по-вашему, он измерял время их падения? Если бы объекты были одного размера, но разной массы, что, по вашему мнению, он должен был бы наблюдать? Был бы этот результат другим, если бы это было сделано на Луне?

PhET Исследования: массы и пружины

Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины. 9{2}\\[/latex], где C  – коэффициент сопротивления (типичные значения приведены в таблице 1), A  – площадь объекта, обращенная к жидкости, а [латекс]\rho\\[ /латекс] — плотность жидкости.

Для небольших объектов (например, бактерий), движущихся в более плотной среде (например, в воде), сила сопротивления определяется законом Стокса, [латекс] {F} _ {\ text {s}} = 6 \ pi \ eta{rv}\\[/latex], где r  – радиус объекта,  η  – вязкость жидкости, а  v  – скорость объекта.

Концептуальные вопросы

1. Спортсмены, такие как пловцы и велосипедисты, на соревнованиях носят комбинезоны. Сформулируйте список плюсов и минусов таких костюмов.
2. Для силы сопротивления, испытываемой движущимся объектом в жидкости, использовались два выражения. Один зависел от скорости, а другой был пропорционален квадрату скорости. К каким видам движения каждое из этих выражений будет более применимо, чем другое?
3. Во время движения автомобилей масло и бензин вытекают на дорожное покрытие. Если идет легкий дождь, как это влияет на управляемость автомобиля? Имеет ли значение сильный дождь?
4. Почему белка может прыгнуть с ветки дерева на землю и убежать невредимой, а человек при таком падении может сломать кость?

Задачи и упражнения

1. Конечная скорость человека, падающего в воздухе, зависит от веса и площади тела человека, обращенного к жидкости. Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м ² .
2. Парашютист весом 60 кг и 90 кг прыгают с самолета на высоте 6000 м, оба падают в положении «согнувшись». Сделайте некоторое предположение об их лобовых площадях и рассчитайте их конечные скорости. Сколько времени потребуется каждому парашютисту, чтобы достичь земли (при условии, что время достижения конечной скорости мало)? Предположим, что все значения имеют точность до трех значащих цифр.
3. Белка массой 560 г с площадью поверхности 930 см ² падает с 5-метрового дерева на землю. Оцените его конечную скорость. (Используйте коэффициент аэродинамического сопротивления для горизонтального парашютиста.) Какова будет скорость человека массой 56 кг, который упадет на землю, при условии отсутствия сопротивления на таком коротком расстоянии?
4. Чтобы поддерживать постоянную скорость, сила, создаваемая двигателем автомобиля, должна равняться силе сопротивления плюс сила трения о дорогу (сопротивление качению). (a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь лобового сопротивления равна 0,70 м ² ) (b) Какова величина силы лобового сопротивления автомобиля Hummer h3 при скорости 70 и 100 км/ч? (Площадь сопротивления составляет 2,44 м ² ) Предположим, что все значения точны до трех значащих цифр.
5. Во сколько раз увеличивается сила сопротивления автомобиля при движении от 65 до 110 км/ч?
6. Рассчитайте скорость, с которой сферическая капля дождя падает с высоты 5,00 км (a) в отсутствие сопротивления воздуха (b) с сопротивлением воздуха. Примем размер капли поперек 4 мм, плотность 1,00 × 10 ³ кг/м ³ и площадь поверхности π r ² .
7. Используя закон Стокса, убедитесь, что единицами измерения вязкости являются килограммы на метр в секунду.
8. Найдите конечную скорость сферической бактерии (диаметром 2,00 мкм), падающей в воду. Сначала вам нужно отметить, что сила сопротивления равна весу при конечной скорости. Примем плотность бактерии равной 1,10 × 10 ³ кг/м ³ .
9. Закон Стокса описывает осаждение частиц в жидкостях и может использоваться для измерения вязкости. Частицы в жидкостях быстро достигают предельной скорости. Можно измерить время, за которое частица падает на определенное расстояние, а затем использовать закон Стокса для расчета вязкости жидкости. Предположим, что стальной шарикоподшипник (плотность 7,8 × 10 ³ кг/м ³ , диаметр 3,0 мм) брошен в емкость с моторным маслом. Падение с высоты 0,60 м занимает 12 с. Рассчитайте вязкость масла. 9{2}\\[/latex], где C  – коэффициент сопротивления, A  – площадь объекта, обращенного к жидкости, а [latex]\rho[/latex] – плотность жидкости

   Закон Стокса: [латекс]{F}_{s}=6\pi{r}\eta{v}\\[/latex] , где r — радиус объекта, η — вязкость жидкости, а  v  – скорость объекта

   Избранные решения задач и упражнений

   1. 115 м/с; 414 км/ч

   9{2}}{\text{m}\cdot \text{m/s}}=\frac{\text{kg}}{\text{m}\cdot \text{s}}\\[/latex]

   9. 0,76 кг/м·с

   Формула силы сопротивления — GeeksforGeeks

   Сила, действующая на твердое тело, движущееся относительно жидкости в результате движения жидкости, известна как сила сопротивления. Например, перетащите движущийся корабль или перетащите летящий самолет. В результате сила сопротивления представляет собой сопротивление, создаваемое телом, движущимся через жидкость, такую ​​как вода или воздух. Эта сила сопротивления противостоит скорости набегающего потока. В результате это скорость тела к жидкости. В этой статье мы рассмотрим концепцию и формулу силы сопротивления на примерах. Давайте посмотрим на идею.

   Что такое сила сопротивления?

   Сила сопротивления (D) — это сила, противодействующая движению тела в жидкости.

   Сила сопротивления жидкости называется силой сопротивления. Эта сила противодействует движению погруженного в жидкость тела. Таким образом, сила сопротивления определяется как сила, противодействующая движению тела в жидкости. При движении тела в жидкообразной среде возникает аэродинамическое сопротивление. Когда жидкость представляет собой воду, это также гидродинамическое сопротивление. Он имеет естественную склонность действовать в направлении, противоположном скорости потока. Сопротивление воздуха часто ограничивает максимальную скорость, с которой может двигаться падающее тело. Сопротивление воздуха — хороший пример силы сопротивления, то есть силы, которую объекты ощущают при движении через жидкость.

   Сила сопротивления, как и кинетическое трение, представляет собой реактивную силу, возникающую только при движении объекта и направленную в направлении, противоположном движению объекта в жидкости. Сопротивление формы и сопротивление кожи — два типа этой силы. Сопротивление формы — это сопротивление жидкости перемещению движущегося объекта. В результате сопротивление формы сравнимо с силой, создаваемой сопротивлением твердых тел деформации. Жидкость, скользящая по поверхности движущегося объекта, вызывает поверхностное сопротивление, которое по существу представляет собой механическую силу трения.

   Формула силы сопротивления 

   Сила сопротивления рассчитывается по следующей формуле:

   D = (C _d × ρ × V ² × A) / 2

   5, где, Д – сила сопротивления (Н),

10. C _d – коэффициент сопротивления,
11. ρ – плотность среды (кг/м ³ ),
12. V – скорость тела (м/с ), а
13. A — площадь поперечного сечения (м ² ).

Примеры вопросов

Вопрос 1: Что такое перетаскивание?

Ответ :

Сопротивление — это сила, с которой поток жидкости действует на объект, движущийся в его направлении, или сила, с которой объект движется в жидкости. Движущиеся транспортные средства, корабли, висячие мосты, градирни и другие конструкции должны оценивать размер конструкции и то, как ее можно уменьшить. Силы сопротивления традиционно представляются коэффициентом сопротивления, который определяется независимо от формы тела.

Коэффициент аэродинамического сопротивления пропорционален числу Рейнольдса, как показывает размерный анализ; точное соотношение должно быть определено экспериментально, но его можно использовать для аппроксимации сил сопротивления, испытываемых другими телами в других жидкостях при других скоростях. Идея динамического подобия используется инженерами, когда они используют эффекты структуры модели для прогнозирования поведения других структур.

Вопрос 2: Автомобиль движется со скоростью 83 км/ч и имеет коэффициент аэродинамического сопротивления 0,30. Определить силу сопротивления, если площадь поперечного сечения равна 12 кв.

Ответ:

Учитывая, что,

В = 83 км/ч = 83 × 5/18 м/с = 23,05 м/с,

C _D = 0,30, A = 12 м ² ,

ρ = 1,2 кг/м ³

Поскольку,

D = (C _d × ρ × V ² × A) / 2 × A) / 2

9004 05 ² × 12) / 2

= 2295,21 / 2

= 1147,60 N

Вопрос 3: При коэффициенте лобового сопротивления 0,25 самолет движется со скоростью 610 км/ч. Рассчитайте силу сопротивления, если площадь поперечного сечения самолета 70 м ² .

Ответ:

Учитывая, что

V = 610 км/ч = 610 × 5/18 м/сек = 169,44 м/сек,

р = 1,2 кг/м ³ ,

A=70 м ²

Так как,

D = (C _d × ρ × V ² × A) / 2

= 1,025 169,44 ² × 70) / 2

= 602908,11 / 2

= 301454,05 N

Вопрос 4: При коэффициенте лобового сопротивления 0,14 велосипед движется со средней скоростью 83 км в час. Рассчитайте силу сопротивления для площади поперечного сечения 5 м ² .

Ответ:

Учитывая, что

V = 83 км/ч = 83 × 5/18 м/сек = 23,05 м/сек,

C _{d2 04 А = 5 м ² ,}

ρ = 1,2 кг/м ³

Так как,

D = (C _d × ρ × V ² × А) / 2

= (0,14 × 1,2 × 23,05 ² × 5) / 2

= 446,292 / 2

= 223,145

9 N

04 Вопрос 5: Что такое коэффициент аэродинамического сопротивления движущегося объекта в воде, который испытывает силу сопротивления 520 Н? Площадь сечения 3 м ² , скорость 20 м/с.