Расчет рулевого управления грузового автомобиля ЗИЛ-131
БНТУ, Автомобили, по дисциплине “Проектирование систем управления автомобилей”, Тема “Рулевое управление грузового автомобиля”, Минск 2014
На основании расчетов и уже существующих конструкций было спроектировано рулевое управление автомобиля. Определены типы, параметры и размеры агрегатов и узлов входящих в состав рулевого управления. Определена его конструкция. Выполнены расчеты на прочность деталей рулевого привода и рулевого механизма. Проведен анализ кинематики рулевого привода по условиям недопущения заклинивания рулевой трапеции и обеспечению заданных углов поворота управляемых колес. Осуществлен гидравлический расчет гидроусилителя рулевого управления. Разработка велась на основании рулевого управления применяемого на автомобиле ЗИЛ-131.
СОДЕРЖАНИЕ
Введение
1 Обзор схем и конструкций рулевых управлений грузовых автомобилей
1.
1 Рулевые механизмы
1.2 Рулевой привод
1.3 Усилители рулевого управления
2 Описание работы, регулировок и технических характеристик проектируемого узла
3 Кинематический расчет рулевого управления
4 Силовой расчет рулевого управления
5 Гидравлический расчет рулевого управления
6 Прочностные расчеты элементов рулевого управления
6.1 Прочностной расчет зацепления поршень-рейка с сектором в рулевом механизме
6.2 Прочностной расчет рулевой сошки
6.3 Прочностной расчет продольной рулевой тяги
6.4 Прочностной расчет поперечной рулевой тяги
7 Заключение
Состав: Рулевой механизм ЗИЛ-131 СБ, СП, ПЗ
Софт: AutoCAD 2012
Файлы:
Готово\КР — копия — копия.
docx
Готово\рулевой механизм зил 131.bak
Готово\рулевой механизм зил 131.dwg
Готово\Содержание.docx
Готово\Спецификация 1+2стр.doc
Готово
Чтобы скачать чертеж, 3D модель или проект, Вы должны зарегистрироваться и принять участие в жизни сайта. Посмотрите, как тут скачивать файлы.
Рейтинг: 500
Софт: КОМПАС-3D 16
Состав: Механизм рулевой (ВО), 3-D рулевого механизма (ВО), Анимация работы рулевого механизма (ВО), Привод рулевой (ВО), Механизм тормозной (ВО), Коробка передач (ВО), Главная передача (СБ), Спецификация, Шестерня (чертеж), Технологическая схема (главная передача), Тяговый расчет (3-D графиками), Схема кинематическая (трансмиссии), ПЗ
Модернизация рулевого управления, коробки передач, главной передачи и тормозного механизма легкового автомобиля класса 2
Автомобили. Проектирование и расчет рулевых управлений: Учебно-методическое пособие
А.
А.
Енаев
Автомобили.
Проектирование и расчет
рулевых управлений
Учебно-методическое пособие
СОДЕРЖАНИЕ
|
1. ОБЩИЕ РЕКОМЕНДАЦИИ ПО ПРОЕКТИРОВАНИЮ РУЛЕВЫХ УПРАВЛЕНИЙ……………………………………. 2. НАЗНАЧЕНИЕ, ТРЕБОВАНИЯ И КЛАССИФИКАЦИЯ… 3. ВЫБОР СПОСОБА ПОВОРОТА АВТОМОБИЛЕЙ……… 4. ВЫБОР СХЕМЫ РУЛЕВОГО УПРАВЛЕНИЯ……………. 5. РУЛЕВЫЕ МЕХАНИЗМЫ………………………………….. 5.1. Назначение, требования, классификация……………… 5.2. Оценочные параметры рулевого механизма………….. 5.3. Выбор типа рулевого механизма………………………. 5.4. Материалы, используемые для изготовления рулевых механизмов…………………………………………………… 6. РУЛЕВЫЕ ПРИВОДЫ………………………………………. 6.1.
Назначение, требования, классификация……………. 6.2. Оценочные параметры рулевого привода…………….. 6.3. Выбор типа рулевого привода…………………………. 6.4. Материалы, используемые для изготовления рулевых приводов……………………………………………………… 7. УСИЛИТЕЛИ РУЛЕВОГО УПРАВЛЕНИЯ……………….. 7.1. Назначение, требования, классификация……………… 7.2. Оценочные параметры усилителя рулевого управления……………………………………………………………. 7.3. Выбор схемы компоновки усилителей………………… 7.4. Насосы усилителей……………………………………… 7.5. Материалы, используемые для изготовления усилителей насосов…………………………………………………… 8. РАСЧЕТ РУЛЕВОГО УПРАВЛЕНИЯ……………………… 8.1. Кинематический расчет рулевого привода……………. 8.2. Передаточное число рулевого управления……………. 9. СИЛОВОЙ РАСЧЕТ РУЛЕВОГО УПРАВЛЕНИЯ………… 9.1. Усилие на рулевом колесе……………………………… 9.2. Усилие, развиваемое цилиндром усилителя………….. 9.3. Усилие
на колесах при торможении…………………. 9.4. Усилия на поперечной и продольной тягах…………… 10. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ УСИЛИТЕЛЯ…………… 11. ПРОЧНОСТНОЙ РАСЧЕТ РУЛЕВОГО УПРАВЛЕНИЯ.. 11.1. Расчет рулевых механизмов…………………………… 11.2. Расчеты рулевых приводов…………………………… СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ……………… |
5 5 7 10 12 12 12 16 18 18 18 19 20 22 22 22 24 25 28 29 29 29 35 36 37 38 39 40 41 42 43 46 48 |
..
..1.
ОБЩИЕ РЕКОМЕНДАЦИИ ПО ПРОЕКТИРОВАНИЮ И РАСЧЕТУ
РУЛЕВЫХ УПРАВЛЕНИЙ
Проектирование и расчет рулевых управлений является одной из составных частей курсового проекта по дисциплине «Автомобили».
На первом этапе курсового проектирования необходимо выполнить тяговый расчет и исследовать эксплуатационные свойства автомобиля, используя методические указания «Автомобили. Общие положения. Тяговый расчет» и затем приступить, в соответствии с заданием, к проектированию и расчету агрегата или системы шасси автомобиля.
При проектировании и расчете рулевых управлений необходимо подобрать рекомендуемую литературу, внимательно ознакомиться с данным пособием. Последовательность работы по проектированию и расчету рулевых управлений такова:
1. Выбрать способ поворота автомобиля, схему рулевого управления, тип рулевого механизма, схему компоновки усилителя (если он необходим).
2.
Выполнить кинематический расчет, силовой расчет, гидравлический расчет
усилителя (если в рулевом управлении предусматривается установка усилителя).
3. Выбрать размеры деталей и выполнить прочностной расчет.
В настоящем учебно-методическом пособии подробно изложено, как выполнить все эти виды работ.
2. НАЗНАЧЕНИЕ, ТРЕБОВАНИЯ И КЛАССИФИКАЦИЯ
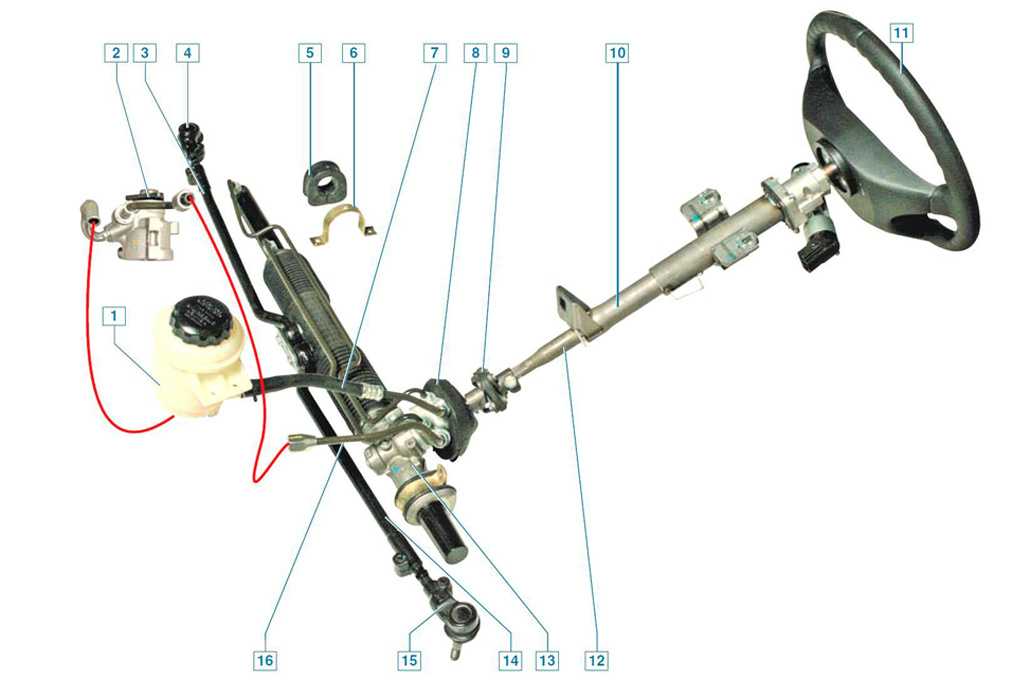
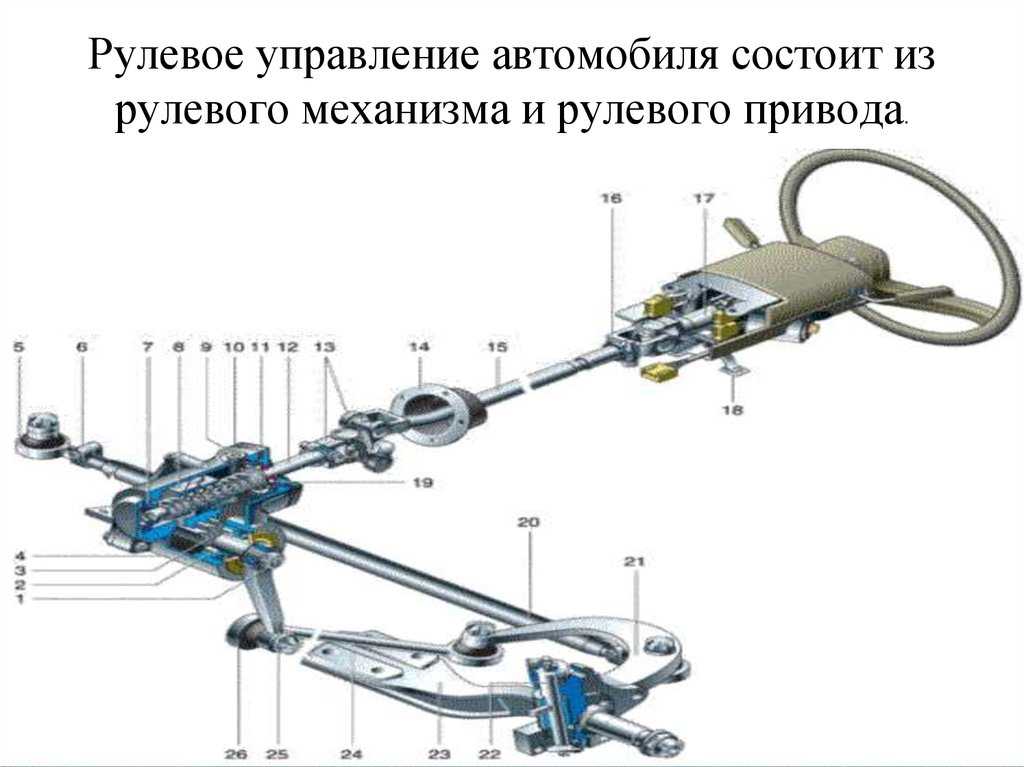
Рулевое управление – это совокупность устройств, служащих для поворота управляемых колес автомобиля при воздействии водителя на рулевое колесо и состоящее из рулевого механизма и привода (рис. 1).
Рулевой механизм – это часть рулевого управления от рулевого колеса до рулевой сошки, а рулевой привод включает детали от рулевой сошки до поворотной цапфы.
Рис. 1. Схема рулевого управления:
1 – рулевое колесо; 2 – рулевой вал; 3 – рулевая колонка; 4 – редуктор; 5 – рулевая сошка; 6 – продольная рулевая тяга; 7 – поворотная цапфа; 8 – рычаг поворотной цапфы; 9 – боковой рычаг; 10 – поперечная тяга
К рулевому управлению предъявляются следующие требования:
1) обеспечение высокой маневренности автотранспортных средств, при которой возможны крутые и быстрые повороты на сравнительно ограниченных площадях;
2) легкость управления, оцениваемая величиной усилия, прикладываемого к
рулевому колесу.
Для легковых автомобилей без усилителя при движении это усилие составляет 50…100 Н, а с усилителем – 10…20 Н. Для грузовых автомобилей усилие на рулевом колесе регламентируется: 250…500 Н – для рулевого управления без усилителя; 120 Н – для рулевого управления с усилителем;
3) качение управляемых колес с минимальным боковым уводом и скольжением при повороте автомобиля;
4) точность следящего действия, в первую очередь кинематического, при котором любому заданному положению рулевого колеса будет соответствовать вполне определенная заранее рассчитанная кривизна поворота;
Техническое объяснение: геометрия рулевого управления Ackermann
Геометрия рулевого управления — один из многих инструментов, находящихся в распоряжении конструктора гоночных автомобилей, чтобы гарантировать, что автомобиль извлекает максимальную производительность из всех четырех шин. В этой статье с техническими пояснениями мы расскажем о происхождении и назначении так называемой геометрии рулевого управления Аккермана, а также о том, как ее вариации могут повлиять на характеристики шин во всем диапазоне эксплуатации автомобиля.
Определение Ackermann Steering
Рассмотрим маневр на повороте на низкой скорости, когда все шины находятся в чистом состоянии качения, а транспортное средство не скользит. По мере движения автомобиля по криволинейной траектории все четыре шины следуют уникальным траекториям вокруг общего центра поворота, обозначенного синими дугами на рис. 1.
Рис. 1: Упрощенное изображение конфигурации рулевого управления AckermannРазличные радиусы кривизны означают, что во избежание скольжения геометрия рулевого управления должна направлять внутреннее переднее колесо на больший угол, чем внешнее переднее колесо. Ackermann Steering относится к геометрической конфигурации, которая позволяет поворачивать оба передних колеса под соответствующим углом, чтобы избежать скольжения шин.
Для заданных радиуса поворота R, колесной базы L и ширины колеи T инженеры рассчитывают требуемые передние углы поворота (δ_(f,in) и δ_(f,out)) по следующим выражениям:
Разница в угле поворота передних колес как функция входного угла поворота называется динамическим схождением.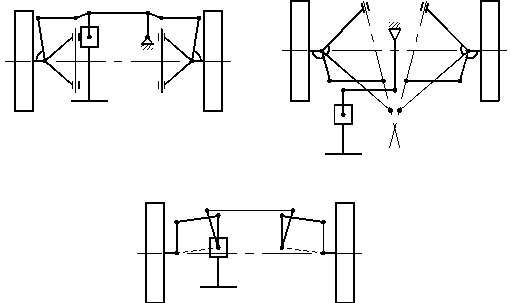
Если размеры транспортного средства известны, можно построить кривую желаемого изменения схождения для всего диапазона ожидаемых радиусов поворота, например, в примере на рис. 2.
Включая углы увода
Транспортному средству, движущемуся по криволинейному пути на скорости, требуется центростремительная сила, обеспечиваемая боковой силой шин, чтобы сохранить траекторию. Центростремительная сила возникает, когда шина принимает угол увода, о котором вы можете узнать больше в этой предыдущей статье с техническими пояснениями .
Последующая разница между направлением шины и ориентацией пятна контакта смещает центр поворота автомобиля вперед, как показано на рис.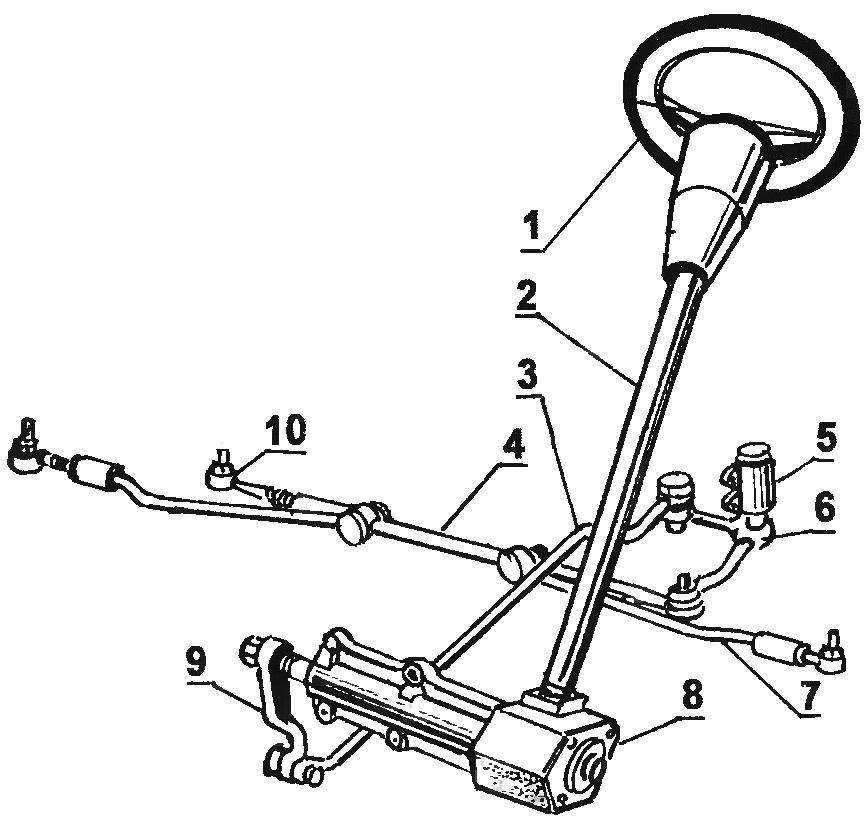
3.
Если шина имеет угол скольжения, присутствующая составляющая скорости поперечного скольжения больше нуля.
По этой причине цель состоит в том, чтобы точно настроить условия скольжения каждой шины, чтобы оптимизировать общую производительность, а не пытаться полностью избежать проскальзывания шины.
Ключом к раскрытию этих характеристик является понимание взаимосвязи между вертикальной нагрузкой и допустимой поперечной нагрузкой в шинах.
На рис. 4 показано соотношение поперечной силы и угла скольжения для шины Indy Lights в диапазоне вертикальных нагрузок.
Рисунок 4: Кривые зависимости поперечной силы от угла скольжения для Cooper Tyres Indy Lights 2017 Передняя шина Чем выше вертикальная нагрузка на шину, тем большую пиковую боковую силу она может создавать. При более высоких вертикальных нагрузках пиковая боковая сила возникает при более высоком угле скольжения.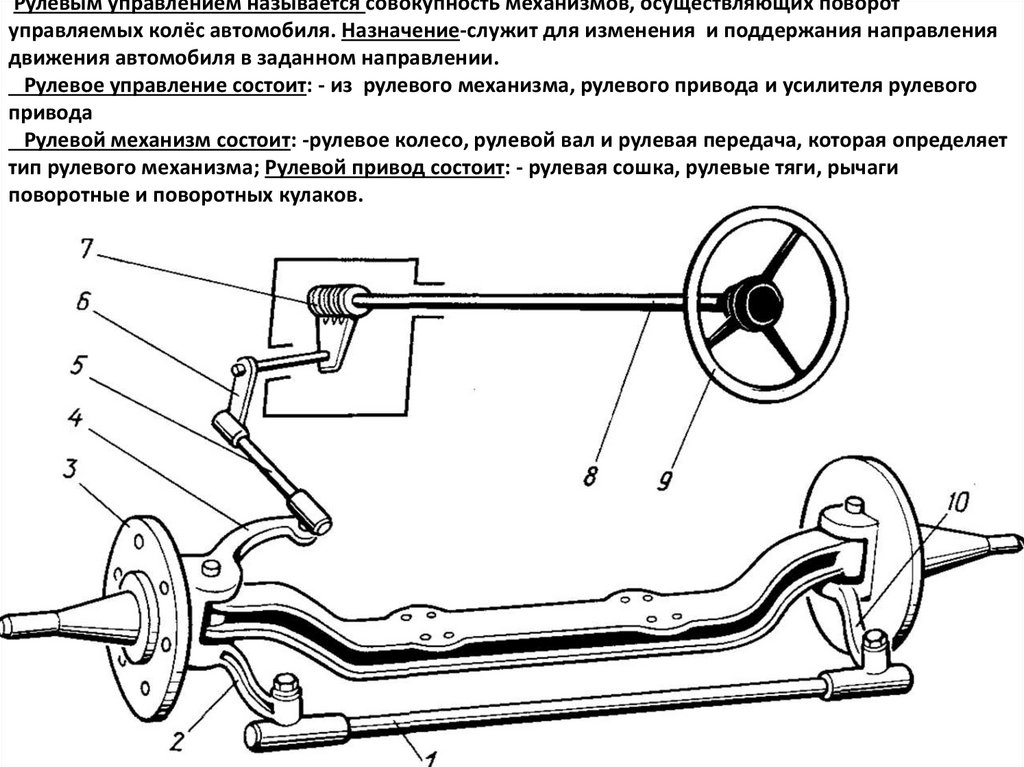
Эта тенденция ожидаема, но не обязательно присутствует во всех шинах и может зависеть от состава или конструкции.
Связь между вертикальной нагрузкой и пиковым углом скольжения известна как линия пиков. Характеристика линии пиков имеет важное значение из-за начала передачи поперечной нагрузки во время маневра в повороте, когда вертикальная нагрузка передается от внутренних шин к внешним шинам.
Крайне важно убедиться, что обе шины работают с максимальным углом увода одновременно, чтобы максимизировать производительность. В случае шины Indy Lights это означает, что более нагруженная внешняя шина должна иметь больший угол скольжения, чем внутренняя шина. Этого можно добиться, управляя внешней шиной больше, чем внутренней, при заданном усилии рулевого колеса.
Результат полностью противоположен Акермановскому рулевому управлению и известен как обратный Акерману или антиаккермановский. Многие гоночные автомобили, оснащенные системой Anti-Ackermann, работают в пиковых условиях эксплуатации отдельных шин.
Designing for Ackermann
Уровень Аккермана в геометрии рулевого управления автомобиля представлен в процентах, где 100% Аккермана означает, что разница в угле поворота между внутренней и внешней шиной соответствует геометрическому центру поворота на низкой скорости.
Большинство гоночных автомобилей не работают на 100% по Акерману или на 100% по Анти-Акерману. Вместо этого они настраивают свое решение где-то посередине, чтобы соответствовать их конкретным целям проектирования и ожидаемым условиям эксплуатации.
При выборе геометрии рулевого управления для гоночного автомобиля конструктор должен учитывать несколько важных моментов. Конструкторы должны понимать профиль скорости и характеристики трассы, по которой машина будет участвовать в гонках.
Чем медленнее и теснее трасса, тем важнее становится нанять Аккермана для помощи в прохождении шпилек и других крутых поворотов, где геометрия доминирует над всем остальным. В то время как автомобиль Формулы-1, проходящий поворот радиусом 200 м, может значительно выиграть от Anti-Ackermann, аналогичная установка серьезно помешает автомобилю Formula Student пройти поворот радиусом 5 м.
шпилька.
Пример использования Anti-Ackermann на автомобиле Red Bull F1 показан на рисунке 5.
Рисунок 5: Пример использования Anti-Ackermann на автомобиле Red Bull F1 (источник: apexspeed.com)Дизайнеры должны использовать автомобиль и характеристики гусеницы для прогнозирования вертикальных нагрузок на все четыре шины на протяжении круга. Фундаментальные факторы могут включать вес, высоту дорожного просвета, распределение поперечной нагрузки и уровни прижимной силы, а сложность анализа может зависеть от доступной информации.
Точная аппроксимация вертикальных нагрузок на всех поворотах может быть объединена с информацией о линии пиков, извлеченной из анализа данных шин, чтобы понять пиковые углы скольжения для обеих передних шин на каждом повороте. Конструкторы могут использовать эту информацию для построения целевой кривой динамического схождения, как показано на рис. 2.
Во многих случаях компоновочные и кинематические ограничения могут сделать невозможным создание геометрии рулевого управления, которая может соответствовать этой целевой кривой для всех углов гусеницы.
Разработчику придется решить, где они готовы пойти на компромисс в производительности.
Наконец, важно помнить, что Ackermann — не единственный способ регулировки угла скольжения отдельных шин. Ударное рулевое управление может быть реализовано кинематически, чтобы вызвать дополнительный угол поворота за счет хода подвески, что инженеры могут использовать, когда автомобиль заходит в поворот.
Кроме того, ни один из компонентов подвески не является абсолютно жестким, и податливость звеньев может повлиять на угол поворота шин в повороте. Предположим, что эти факторы хорошо изучены и интегрированы в систему подвески.
В этом случае это может помочь устранить описанные выше компромиссы, но если их игнорировать или неправильно понимать, это может привести к непредсказуемому поведению на поворотах и снижению производительности.
геометрия — Как найти конечный угол автомобиля после руления?
Сначала создайте функцию, описывающую угол поворота рулевого колеса как функцию времени.
В данном случае, похоже,
$$\тета(т) = \begin{случаи}
\frac{15\text{°}}{1\;\text{s}} t, & 0\;\text{s} \le t \lt 2\;\text{s} \\
30\text{°}, & 2\;\text{s} \le t \lt T + 2\;\text{s} \\
\frac{15\text{°}}{1\;\text{s}} (T + 4\;\text{s} — t), & T + 2\;\text{s} \le t \ ле Т + 4\;\text{s} \\
\end{case} \tag{1}\label{NA1}$$
где и $T$ — продолжительность удержания угла поворота руля на уровне $30\text{°}$. Обратите внимание, что $\text{°}$ и $\text{s}$ не являются переменными, а обозначают угловые и временные единицы (градусы и секунды) соответственно. Затем постройте функцию $\dot{\varphi}(t)$, описывающую скорость поворота автомобиля как функцию времени при заданном угле поворота $\theta(t)$ и скорости автомобиля $v $.
Если расстояние между осями $L = 4\;\text{m}$, радиус поворота равен $r(\theta)$,
$$r(\theta) = \frac{L}{\tan(\theta)}$$
При радиусе поворота $r(\theta)$, если автомобиль движется со скоростью $v$ в течение времени $t$, он проходит $v t$ по периметру круга поворота и, таким образом, поворачивает на $\phi(\theta , v, t)$,
$$\phi(\theta, v, t) = \frac{v t}{2 \pi r(\theta)} 360\text{°} = \frac{v t \tan(\theta)}{2 \pi L} 360\text{°}$$
Таким образом, мгновенная скорость поворота автомобиля равна
$$\dot{\varphi}(t) = \frac{d \phi(\theta, v, t)}{d t} = \frac{v \; 360\text{°}}{2 \pi L} \tan\left(\theta(t)\right) \tag{2}\label{NA2}$$ 92} \приблизительно \frac{v}{L} 31,48015\text{°s} \tag{3.
Если $v = 10\;\text{м/с}$ и $L = 4\;\text{m}$ , тогда $$\varphi(T) \приблизительно 157,401\текст{°} + 82,6993\текст{°} \; T$$
В обмене комментариями OP указывает, что неясно, как $\eqref{NA2}$ дает $\eqref{NA3.1}$. Давайте расширим это, надеюсь, таким образом, что это поможет другим, работающим над аналогичными проблемами. Хотя для вывода формул требуется немного математических вычислений, я покажу, как использовать бесплатный SageMath с открытым исходным кодом, чтобы сделать математическое фу за вас.
Во-первых, нам нужна мгновенная скорость поворота $\dot{\varphi}(t)$. Оказывается, что $\eqref{NA2}$ является правильной формой для автомобиля с изменяющимся углом поворота руля $\theta(t)$, даже если скорость автомобиля $v(t)$ меняется, пока расстояние между осями $ L$ постоянна.
2$ (так что $a(0) = 0$, $a( 5) = 5$ и $a(10) = 0$), вы можете вычислить $v(t)$ в Sagemath следующим образом: 93$.
Аналогично для угла поворота $\theta(t)$. Я называю это theta = var('theta') в SageMath, но решать вам, конечно.
Обратите внимание, что в большинстве систем компьютерной алгебры и языков программирования используются радианы, а не градусы. 360° соответствует $2\pi$ радианам. Чтобы преобразовать $x$ градусов в радианы, используйте $x \pi / 180$. Чтобы перевести $y$ радиан в градусы, используйте $180 y/\pi$. Это причина для *pi/180 в tan() ниже.
Чтобы превратить $\eqref{NA5}$ в изменение угла поворота рулевого колеса, нам нужно проинтегрировать мгновенное изменение направления автомобиля $\dot{\varphi}(t)$ за время $t$. Предположим, что наши функции действительны с момента времени от $t = t_0$ до $t = t_1$, и изменение направления автомобиля за это время равно $\varphi_\Delta$:
$$\varphi_\Delta = \int_{t_0}^{t_1} \dot{\varphi}(t) d t \tag{6}\label{NA6}$$
Чтобы вычислить это, нам нужен исчисление или кто-то или что-то, кто сделает это за нас.
{N-1} \dot{\varphi }\left(t_0 + \frac{2 i + 1}{2 N} t_1 \right)$$
То есть мы суммируем $N$ слагаемых, каждое слагаемое равно $\dot{\varphi}$ в середине интервала, а затем умножаем сумму на ширину каждого интервала. Шаг по времени, размер каждого временного интервала, равен $\frac{t_1 — t_0}{N}$. Чем больше $N$, тем меньше временной шаг и тем точнее результат (поскольку «ступенчатая кривая», которую мы на самом деле интегрируем, лучше соответствует фактической кривой $\dot{\varphi}(t)$).
(Если вы сэмплируете кривую в начале каждого интервала, в $\dot{\varphi}(t_0 + \frac{i}{N} t_1)$, ответ такой же хороший; это просто не «средняя точка » по существу, но начальное значение на каждом интервале. «Кривая шага» смещена на половину шага по времени раньше, вот и все.)
Так как мы знаем скорость автомобиля $v$ и угол поворота руля $\ theta$ (относительно текущего направления автомобиля, поэтому $\theta = 0$ — вперед, $\theta > 0$ — поворот влево/против часовой стрелки, а $\theta < 0$ — поворот вправо/по часовой стрелке), мы знаем $\ точка {\ varphi} (t) $, а также.