11Июн

Коэффициент сопротивления воздуха таблица: Коэффициент сопротивления некоторых тел

11 Июн 2023 alexxlab Комментировать

Коэффициент сопротивления некоторых тел

Плоская пластина, установленная под углом 90° к потоку …………………..1,28

Парашютист, падающий плашмя, с разведенными в стороны ногами и руками…………………………………………………………………………..0,35

Парашютист, падающий в группировке, под углом 45° к горизонту ………0,2

Двухоболочковая парашютная система ……………………………………………….1.2

Парашют круглой формы при вертикальном снижении…………………………0,9

Зная лобовое сопротивление тела, легко подсчитать сопротивление, испытываемое телом при падении или куполом парашюта при парашютировании.

Снижение парашютиста

Скорость падения парашютиста зависит от времени падения, плотности воздушной среды, площади падающего тела и коэффициента его лобового сопротивления. На скорость падения масса падающего тела влияет незначительно.

Ввиду того, что спортивные и тренировочные прыжки с парашютом выполняются из самолетов, летящих на небольших скоростях, влияние

54

начальной горизонтальной скорости на вертикальную скорость падения при расчетах не учитывается.

Если начальная вертикальная скорость равна нулю, то расстояние, пройденное телом до тех пор, пока скорость невелика, будет зависеть только от одной величины — ускорения силы тяжести g и пройденный путь можно определить по формуле

,

где t — время падения, с.

С нарастанием скорости вступает в силу целый ряд других факторов.

На падающее в воздушной среде тело действуют две силы: сила тяжести G, всегда направленная вниз, и сила сопротивления воздуха Q, направленная в сторону, противоположную направлению перемещения тела. Если отсутствует горизонтальная составляющая скорости, то сила сопротивления воздуха направлена против силы тяжести (рис.

39).

Скорость падения будет возрастать до того момента, пока силы G и Q не уравновесятся:

Это состояние называется установившимся падением, а соответствующая ему скорость — предельной (критической) или равновесной скоростью.

Критическая (равновесная) скорость определяется по формуле

Эта скорость при Сх парашютиста 0,3 будет равна 42 м/с, а при Сх

парашютиста 0,15 — 58 м/с.

Поскольку плотность воздуха с высотой меняется, то и

скорость падения будет постоянно меняться.

Расстояние, проходимое парашютистом за время падения с высоты 1500—2000 м в зависимости от положения тела, показано в табл. 2.

С увеличением массы парашютиста увеличивается и скорость его падения. При этом, однако, надо учитывать, что увеличение массы парашютиста всегда связано с увеличением миделя тела, а следовательно, и с увеличением сопротивления воздуха, что в среднем приводит к незначительному увеличению скорости. Ориентировочно можно считать, что изменение массы парашютиста на 10 кг вызывает изменение скорости при установившемся падении на 2%, что у поверхности земли составит

55

разницу в 1 м/с

Рис. 39. Противодействие сил при падении парашютиста.

Нагрузки при раскрытии парашюта. При введении парашюта в действие происходит снижение приобретенной при падении скорости. Из механики известно, что всякое изменение скорости в единицу времени по величине или направлению называется ускорением.

Если, например, скорость в начале движения была V1, а через время t стала V2, то среднее ускорение определяют по формуле

,

где а — ускорение;

V1 — скорость в начале движения; V2— скорость в конце движения;

t— время, за которое произошло изменение скорости.

56

Таблица 2

Время падения, с

Положение тела

Устойчивое вниз головой

Неустойчивое

Устойчивое плашмя

Расстояние, пройденное телом, м

1

4,9

4,9

4,9

2

19,5

19,5

19,5

3

44

43,8

43,5

4

76

75

73,5

5

114

110

105

6

160

150

140

7

210

193

178

8

262

240

218

9

318

287

255

10

375

335

300

11

430

380

342

12

488

430

384

13

546

480

426

14

601

530

468

15

660

580

510

16

718

630

552

17

776

680

594

18

834

730

636

19

892

780

678

20

950

830

720

21

1008

880

762

22

1066

930

804

23

1124

980

846

24

1182

1030

888

25

1240

1080

930

26

1298

1130

972

27

1356

1180

1014

28

1414

1230

1056

29

1470

1280

1098

30

1530

1330

1140

Зная скорость в начале и конце движения, например, при раскрытии парашюта, а также время, за которое происходит его полное раскрытие, можно определить величину среднего ускорения.

Если принять скорость падения VI, равной 50 м/с, скорость после раскрытия парашюта V2, равной 5 м/с, и время t, за которое произошло полное раскрытие парашюта, равным 2 с, то получим

57

Знак минус указывает на замедление (торможение) скорости падения.

Зная, что ускорение при свободном падении равно 9,8 м/с, определим, во сколько раз увеличилось ускорение, т.е. какова величина перегрузки:

Имея данные о перегрузке, легко определить и нагрузку F, действующую на тело в момент раскрытия парашюта. Ее вычисляют по формуле

F = mgn.

При массе парашютиста 70 кг получим

F = 70 • 9,81 • 2,3 = 1579,4H(161/kгс).

Это значит, что, парашютист в момент раскрытия парашюта как бы «прибавляет» в массе на величину, пропорциональную перегрузке. Такие перегрузки человек переносит легко, тем более что они возникают не мгновенно, а достигают максимальной величины через 2 с, за которые происходит изменение скорости.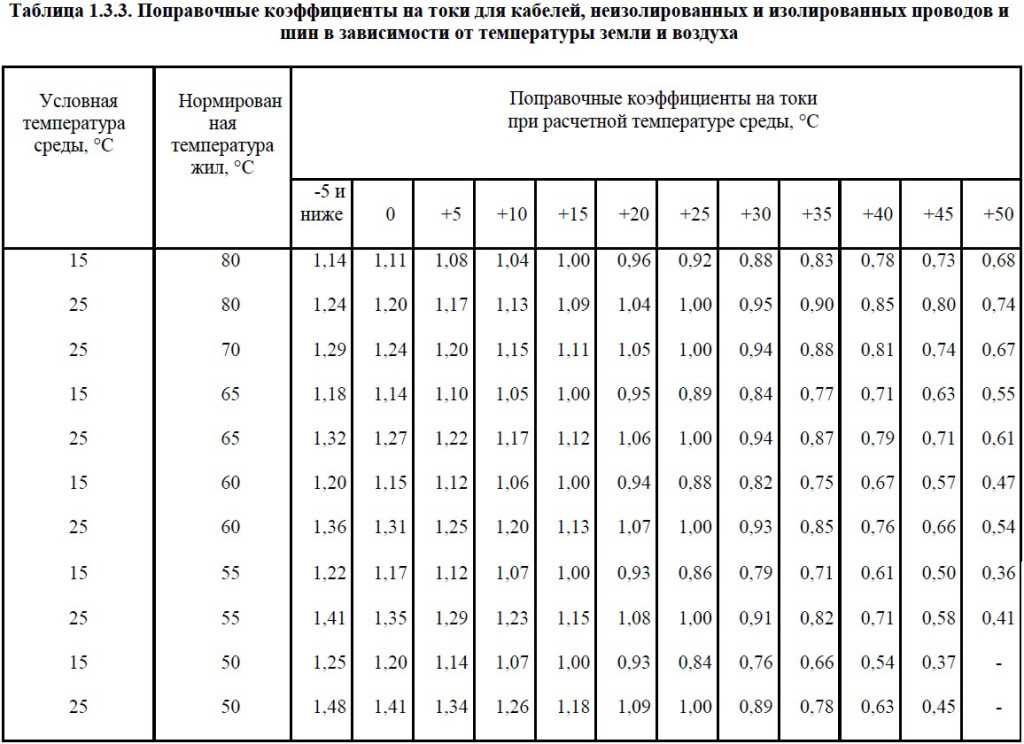

Скорость снижения с раскрытым парашютом. При установившейся скорости снижения с парашютом, не имеющим собственной горизонтальной скорости, сила сопротивления купола Q находится в равновесии с силой тяжести G. Силы в этом случае располагаются, как это указано на (рис. 39). Когда равновесие достигнуто, т. е. G=Q, тогда

.

Если то

Отсюда скорость снижения у земли для парашютной системы будет

Если принять силу тяжести системы G=90 кгс, коэффициент лобового сопротивления Сх=0,9, а площадь купола парашюта S=55 м , то получим

,

что соответствует снижению с куполом парашюта УТ-15. Современные спортивные парашюты имеют собственную горизонтальную скорость. Это дает им возможность перемещаться при снижении не только вместе с воздушной массой по отношению к земле, но и относительно воздушной массы в том или ином направлении. Собственная горизонтальная скорость возникает у купола за счет реактивного эффекта, получаемого при выходе воздуха через отверстия в куполе.

Из аэродинамики известно, что в результате перемещения тела в воздушной среде, силе, действующей на тело по оси перемещения, противодействует сила сопротивления воздуха. При условии равенства этих сил движение по оси перемещения будет равномерным. При увеличении одной из сил возникает дополнительная сила, направленная перпендикулярно линии движения. В аэродинамике эта сила называется подъемной и обозначается буквой Y.

Рис. 40. Схема разложения сил при парашютировании с планирующим куполом:

G — общий полетный вес системы «парашютист + парашют»; Q — сила лобового сопротивления; Y -подъемная сила; W — скорость парашютирования;

R — результирующая сила.

Сила эта невелика и поднять купол вверх, как например при полете самолета, она не может, но оказывает существенное влияние на скорость снижения при прыжках с парашютом, имеющим собственную горизонтальную скорость перемещения, и с ней необходимо считаться.

Рассмотрим схему разложения сил при снижении с таким куполом (рис. 40). С появлением у парашютной системы собственной горизонтальной скорости возникает, как указывалось выше, подъемная сила Y, величина которой зависит от силы сопротивления системы, действующей в направлении движения. Указанные на (рис. 40) силы Q и Y равны между собой и определяются по формуле

в которой коэффициент Сх и площадь S берутся по миделю площади системы в проекции на плоскость снижения.

Рассмотрим, как влияет подъемная сила на парашютирование с различными горизонтальными скоростями.

59

Без горизонтальной скорости, как мы определили выше, система при G = 90 кгс будет снижаться со скоростью 5,4 м/с.

Для определения силы, действующей на парашютную систему, перемещающуюся в горизонтальном направлении (парашют УТ-15 в штилевую погоду), необходимо подсчитать значения Y и Q и найти их результирующую r qy , так как именно эта результирующая противодействует силе тяжести G. Для определения истинной скорости снижения парашютной системы возьмем следующие данные: Vrop=5 м/с (купол УТ-15 при снижении м штилевую погоду), Сх купола = 1,2, a S = 35 м2. Определим по этим данным Ql.

кгс

Если Q = Y, то и Y=54 кгс.

Как известно, результирующая двух перпендикулярных сил равна

кгс

Следовательно, парашютная система будет как бы «легче» на эту величину. Подставляя полученное значение в формулу скорости снижения, определим истинную скорость снижения системы

м/с

При еще большем значении Q (если купол парашюта развернуть, например, против ветра, дующего со скоростью 8 м/с) эффект подъемной силы будет более значительным — вертикальная скорость снижения составит всего 3—3,5 м/с. 5. Для числа Рейнольдса справедлива следующая формула:

где D — диаметр цилиндра, U — скорость потока, p — плотность, m— динамическая вязкость.

Коэффициент сопротивления цилиндра определяется следующим образом:

‍

где FD — сила сопротивления, D диаметр цилиндра, L — длина цилиндра.

Цель данного моделирования — определить коэффициент сопротивления цилиндра с помощью FloEFD и сравнить полученное значение с экспериментальным.

‍

Открытие модели

Скопируйте папку B2 — Drag Coefficient в свою рабочую директорию и убедитесь, что с файлов снят атрибут «только для чтения», так как FloEFD будет сохранять в них входные данные. Кликните Кнопка приложения > Открыть. В диалоговом окне Открыть файл перейдите к сборке Cylinder 0.01m.asm, расположенной в папке B2— Drag Coefficient\cylinder 0.01m, и кликните Открыть.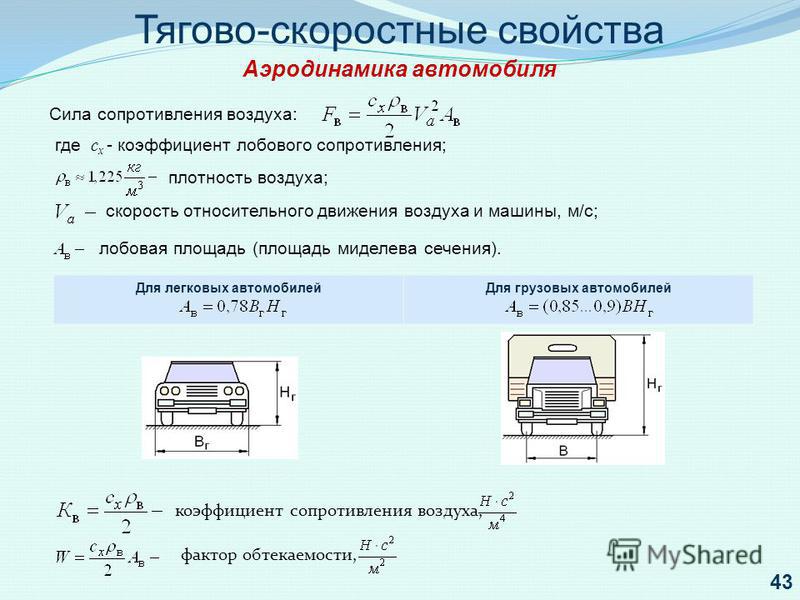

‍

Вы можете пропустить создание проекта и запустить на расчет готовый проект FloEFD, созданный в соответствии с этим примером. Для этого Вам необходимо открыть сборку Cylinder 0.01m.asm, расположенную в папке B2 —Drag Coefficient\cylinder 0.01m\Ready To Run, или сборку Cylinder 0.01m.asm, расположенную в папке B2 — Drag Coefficient\cylinder 1m\Ready To Run, и запустить на расчет нужные проекты.

‍

Рассматриваемая в данном примере задача является внешней задачей FloEFD.

‍

‍

‍Внешняя задача — это задача обтекания каких-либо тел (самолетов, автомобилей, зданий и т.д). В таких задачах границами расчетной области являются внешние границы — плоскости расчетной сетки, параллельные координатным плоскостям и полностью лежащие в области текучей среды. Внешние границы могут пересекать стенки модели. FloEFD позволяет также решать задачи, в которых одновременно присутствует как внешнее, так и внутреннее течение (например, обтекание здания потоком воздуха и воздухообмен внутри него). В этом случае следует задавать Внешний тип течения.

‍

Сначала необходимо создать проект FloEFD.

1. Кликните Flow Analysis > Проект > Мастер проекта. Мастер проекта поможет Вам пошагово создать новый проект FloEFD. В первом случае примем число Рейнольдса равным 1.

2. В диалоговом окне Имя проекта введите имя нового проекта: Re 1. Кликните Далее.

‍

‍

3. В диалоговом окне Система единиц измерения необходимо выбрать систему единиц, которая будет использоваться как для входных, так и для выходных данных (результатов). В данном проекте удобно использовать заданную по умолчанию Международную систему единиц SI. Кликните Далее.

‍

‍

4. В диалоговом окне Тип задачи выберите Внешняя. Также здесь можно указать физические модели, которые будут включены в проект. В данном случае физические модели задавать не будем.

‍

‍

Чтобы пренебречь отдельными замкнутыми областями внутри тела, следует включить опцию Исключить внутреннее пространство. Однако в рассматриваемом цилиндре такие области отсутствуют. Базовая ось глобальной системы координат (X, Y или Z) используется для того, чтобы данные можно было задать в виде таблиц или формул в цилиндрической системе координат с указанной осью вращения.

При числе Рейнольдса Re < 40 обтекание цилиндра является стационарным, при Re > 40 — нестационарным. В рассматриваемом случае при Re=1 задача считается стационарной.

‍

Кликните Далее.

5. В данной задаче исследуется течение воды, поэтому в качестве текучей среды из списка Жидкости выберите Water. Кликните Далее.

‍

‍

6. Тепловое условие, задаваемое в диалоговом окне Условия на стенках по умолчанию, будет относиться ко всем стенкам модели, контактирующим с текучей средой. 5) в диалоговом окне Начальные и внешние условия необходимо задать параметры невозмущенного потока. Таким образом будут определены начальные условия внутри Расчетной области и условия на границах Расчетной области. Внешними условиями являются термодинамические параметры (статическое давление и температура), скорость и параметры турбулентности. В данном проекте используем термодинамические параметры, заданные по умолчанию (давление 101325 Pa и температура 293,2 K). Необходимо только задать скорость входящего потока (в данном случае X-компоненту) в соответствии с числом Рейнольдса:

‍

Чтобы задать скорость потока в этом случае, необходимо открыть диалоговое окно Зависимость.

7. Кликните в поле Скорость в направлении X. Кнопка Зависимость станет активной.

8. Нажмите кнопку Зависимость. Появится диалоговое окно Зависимость.

‍

‍

В диалоговом окне Зависимость данные можно задавать различными способами: в виде констант, формул или функций от x, y, z, q, ф, радиуса r и времени t (только для нестационарных задач). Радиусом r является расстояние от какой-либо точки до Базовой оси, выбранной в соответствии с системой координат (в Мастере проекта и в диалоговом окне Общие настройки это Глобальная система координат). Q и ф — полярный и азимутальный углы сферической системы координат. Таким образом, с помощью координат r, q, и ф данные можно задавать как в цилиндрической, так и в сферической системах.

‍

9. Из списка Тип зависимости выберите Задание формулой.

10. В поле Формула введите выражение для скорости потока при определенном числе Рейнольдса: 1*(0.0010115/0.01/998.19). Здесь: 1 – число Рейнольдса (Re) 0.0010115 (Pa*s) — динамическая вязкость (m) при заданной температуре 293.2 K 0.01 (m) — диаметр цилиндра (D) 998.19 (kg/m3)- плотность воды () при заданной температуре 293.2 K.

‍

‍

11. Кликните OK. Вы вернетесь в диалоговое окно Начальные и внешние условия. В большинстве случаев сложно заранее оценить интенсивность турбулентности течения. Поэтому рекомендуется использовать параметры турбулентности, заданные по умолчанию. Для внешних задач интенсивность турбулентности по умолчанию задана равной 0.1%, для внутренних — 2%. Как правило, эти значения являются подходящими. В данном проекте примем значение 0.1%. Кликните Завершить.

‍

‍

Чтобы уменьшить процессорное время и необходимую для расчета память, решим двумерную задачу (без учета трехмерных эффектов).

‍

Задание 2D моделирования

1. В дереве анализа FloEFD раскройте группу Входные данные.

2. Правой кнопкой мыши кликните по элементу Расчетная область и из контекстного меню выберите Изменить.

3. В группе Тип нажмите кнопку 2D и выберите плоскость XY плоскость (т. к. ось цилиндра — Z).

4. В группе Размеры и условия для границ Расчетной области Z min и Z max автоматически будет задано условие Симметрия.

‍

‍

Границы Z min и Z max устанавливаются автоматически в зависимости от размеров модели. Таким образом, длина цилиндра L, необходимая для расчета коэффициента сопротивления (CD), равна L = Z max-Z min = 0.002 m.

‍

В большинстве случаев, для того, чтобы исследовать обтекание тела и определить, как на этот процесс влияют конструктивные изменения, рекомендуется использовать Расчетную область, сгенерированную FloEFD автоматически. Однако в данном случае результаты, полученные с помощью FloEFD, будут сравниваться с точными экспериментальными данными. Границы Расчетной области расположены близко к цилиндру, из-за чего могут возникать возмущения входящего потока. Это может повлиять на получаемые результаты. Поэтому границы расчетной области необходимо установить на более отдаленном расстоянии от цилиндра. Увеличение размеров Расчетной области позволит снизить требуемые для расчета ресурсы компьютера.

‍

5. В группе Размеры и условия задайте координаты X и Y границ Расчетной области так, как показано на рисунке справа.

6. Кликните OK .

‍

‍

Так как входящий поток направлен вдоль оси X, коэффициент сопротивления цилиндра рассчитывается, исходя из X-компоненты силы сопротивления.

X-компонента силы сопротивления может быть рассчитана с помощью соответствующей цели FloEFD. В данном примере в качестве Глобальной цели необходимо задать параметр Сила (X). Это гарантирует, что расчет не завершится до тех пор, пока не будет достигнута полная сходимость цели по параметру Сила (X) во всей расчетной.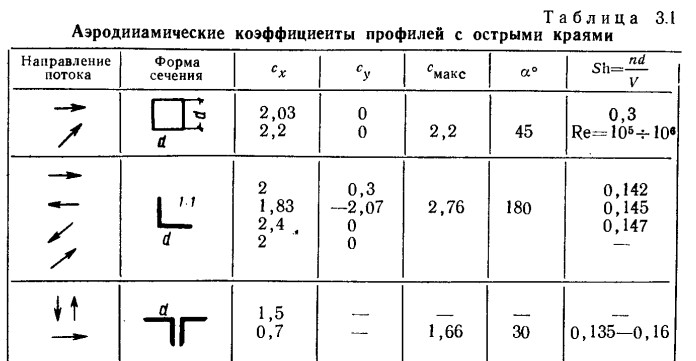

‍

Задание глобальной цели

1. Кликните Flow Analysis > Добавить > глобальные цели.

2. В таблице Параметр поставьте галочку напротив параметра Сила (X).

3. Не снимайте галочку Исп. для сход., чтобы эта цель использовалась для контроля сходимости.

‍

‍

При выборе x, y, z-компонент силы (или момента) Вы можете выбрать Координатную систему, в которой будут рассчитываться эти цели. В данной задаче удобно использовать заданную по умолчанию Глобальную систему координат.

‍

4. Кликните OK . В дереве анализа FloEFD появится элемент ГЦ Сила (X) 1.

‍

Задание цели-выражения

Когда расчет завершится, Вы сможете вручную рассчитать коэффициент сопротивления цилиндра исходя из полученного значения силы. Если же Вы зададите Цель-выражение, это значение будет автоматически рассчитано FloEFD. 5 будет использоваться модель Cylinder 0.01m.asm.

‍

Задание настроек глобальной сетки

1. В дереве анализа FloEFD дважды кликните правой кнопкой мыши по элементу Cетка > Глобальная сетка.

2. По умолчанию выбран Автоматический режим.

3. В группе Настройки задайте Уровень начальной сетки равным 5 и оставьте заданные по умолчанию Минимальный зазор и Коэффициент разбега до границ расчетной области.

4. Кликните OK.

‍

‍

Задание настроек локальной сетки

Для того, чтобы подробно разрешить локальную область вблизи цилиндра, зададим настройки Локальной сетки.

1. Кликните правой кнопкой мыши по элементу Сетка и из контекстного меню выберите Добавить локальную сетку.

2. В графической области выберите боковую поверхность цилиндра.

Поставьте галочку Равноудаленное дробление и в этой группе задайте Число оболочек = 1, Максимальный уровень равноудаленного дробления = 1 и Отступ 1 = 0.004 m.

‍

‍

Адаптирование сетки в процессе расчета

Уровень начальной сетки был задан равным 5, но этого значения недостаточно для точного разрешения вихревой дорожки позади цилиндра. Для того, чтобы улучшить качество решения в этой области, следует произвести адаптирование сетки в процессе расчета.

1. Кликните Flow Analysis > Опции управления расчетом.

2. Перейдите на вкладку Адаптация сетки.

3. В группе Глобальная область выберите уровень = 1.

4. Раскройте группу Настройки адаптации сетки и убедитесь, что в качестве Стратегии адаптации сетки выбрано Таблично.

‍

‍

5. Перед тем, как отредактировать таблицу адаптаций сетки, убедитесь, что в качестве Единиц измерения выбраны Продувки. Затем нажмите кнопку в поле Таблица адаптаций сетки.

6. В появившемся окне кликните Добавить строку. Появится пустая строка.

7. Введите в эту строку значение 2. Это означает, что дробление сетки в процессе расчета произойдет, когда число продувок достигнет 2.

8. Кликните OK. Перейдите на вкладку Завершение.

9. Убедитесь, что в группе Условия завершения включено условие Адаптации сетки.

10. Выключите условие Продувки.

11. Кликните OK.

‍

‍

Клонирование проекта

1. В дереве анализа FloEFD правой кнопкой мыши кликните по элементу Re 1 и из контекстного меню выберите Клонировать проект.

2. В поле Имя проекта введите Re 1000.

‍

‍

3. Кликните OK. Будет создан новый проект FloEFD с прикрепленными к нему данными FloEFD.

‍

‍

Так как новый проект является копией FloEFD проекта Re 1, необходимо изменить только значение скорости течения в соответствии в с числом Рейнольдса 1000. Чтобы изменить данные, определенные в Мастере проекта, воспользуйтесь диалоговым окном Общие настройки. Настройки Единиц измерения и настройки разрешения геометрии не требуют изменений.

‍

В окне Общие настройки представлены текущие настройки проекта. Здесь Вы можете внести изменения в соответствии с требованиями проекта. Таким образом можно менять настройки, заданные в Мастере проекта, или проект, созданный с помощью Шаблона FloEFD.

‍

Изменение настроек проекта

1. Кликните Flow Analysis > Общие настройки. Появится диалоговое окно Общие настройки.

2. Как уже было сказано ранее, при Re > 40 обтекание цилиндра является нестационарным. Поэтому в проекте необходимо включить опцию Нестационарность.

3. В Навигаторе кликните по вкладке Начальные и внешние условия.

‍

‍

4. Кликните в поле Скорость в направлении X и нажмите кнопку Зависимость

‍

‍

5. В поле Формула введите формулу с новым числом Рейнольдса: 1e3*(0.0010115/0.01/998.19).

6. Кликните OK, чтобы вернуться в диалоговое окно Общие настройки.

7. Кликните OK, чтобы сохранить изменения и выйти из диалогового окна Общие настройки.

‍

‍

Изменение цели-выражение

1. В группе Цели кликните правой кнопкой мыши по элементу Коэффициент сопротивления и из контекстного меню выберите. 5, необходимо увеличить диаметр цилиндра до 1 м.

Если необходимо создать подобный проект для одной и той же модели, предпочтительнее использовать клонирование проекта. Для того, чтобы общие настройки проекта применить к другой модели, следует воспользоваться Шаблоном FloEFD.

‍

Шаблон включает в себя основные настройки проекта, которые могут служить основой для нового проекта. Это тип задачи, физические модели, текучие среды, материалы, начальные и внешние параметры течения, тепловое условие на стенке, настройки разрешения геометрии, а также система единиц измерения. Обратите внимание, что Граничные условия, Вентиляторы, Начальные условия, Цели и другие элементы, доступные из группы Flow Analysis > Добавить, в шаблоне не хранятся. По умолчанию доступен только шаблон Internal Water, но Вы также можете создать свои собственные шаблоны.

‍

Создание шаблона

1. Кликните Flow Analysis > Проект > Создать шаблон. Появится диалоговое окно Создать шаблон.

2. В поле Имя шаблона введите Сопротивление цилиндра.

3. Кликните Сохранить. Будет создан новый шаблон FloEFD.

‍

‍

‍

Все шаблоны сохраняются в виде файлов .fwp в директории <install_dir>/Template. Вы можете с легкостью можете применить шаблон к любым ранее созданным моделям.

‍

4. Сохраните модель.

Теперь на основе шаблона Сопротивление цилиндра необходимо создать новый проект.

‍

Создание проекта на основе шаблона

Откройте файл Cylinder 1m.asm, расположенный в папке cylinder 1m.

1. Кликните Flow Analysis > Проект > Новый. Появится диалоговое окно Новый FloEFD проект.

2. В поле Имя конфигурации введите Re 1e5.

3. Из Списка шаблонов выберите Сопротивление цилиндра.

4. Кликните OK.

‍

‍

Новый проект содержит такие же настройки, как и проект Re 1000, поставленный в модели cylinder001m. Другими являются только Разрешение геометрии и размеры Расчетной области, который рассчитываются FloEFD, исходя из геометрических размеров модели. Обратите внимание, что настройки 2D моделирования и Глобальная цель сохранились. Поэтому Вы можете изменить эти настройки в соответствии с новой геометрией модели.

1. Кликните Flow Analysis > Расчетная область и измените размеры расчетной области, как показано на рисунке.

2. Кликните OK.

3. Откройте диалоговое окно Общие настройки, кликните по вкладке Начальные и внешние условия, затем кликните в поле Скорость в направлении X и нажмите кнопку Зависимость. 2)*(2*998.19*1).

‍

‍

8. В качестве Размерности выберите Безразмерный.

9. В поле Имя цели введите Коэффициент сопротивления.

10. Кликните OK .

11. Откройте диалоговое окно Настройки локальной сетки.

12. В группе Равноудаленное дробление установите Отступ 1 = 0.4 m.

Теперь Вы можете рассчитать проекты, поставленные в двух различных конфигурациях.

‍

Запуск серии расчетов

FloEFD позволяет автоматически рассчитать серию проектов, открытых в ткущей сессии.

1. Кликните Flow Analysis > Расчет > Серия расчетов.

2. Поставьте галочку Расчет в поле Все проекты. Таким образом, Расчет будет выбран для всех проектов (Re 1, Re 1000, Re 1e5). Также в поле Все проекты поставьте галочку Закрыть монитор. Когда поставлена галочка Закрыть монитор, после окончания расчета FloEFD автоматически закрывает Окно монитора.‍

3. Кликните Запустить.

‍

‍

Получение результатов

После того, как все расчеты завершатся, перейдите в модель cylinder 0.01m и активируйте проект Re 1000 в дереве проектов FloEFD. Чтобы получить значение Коэффициента сопротивления, создайте Цель:

1. В дереве анализа FloEFD правой кнопкой мыши кликните по элементу Результаты и из контекстного меню выберите Загрузить.

2. В дереве анализа FloEFD в группе Результаты кликните правой кнопкой мыши по элементу Цели и из контекстного меню выберите Добавить. Появится диалоговое окно Цель.

3. Выберите Все.

‍

‍

4. Кликните OK . Будет создан документ Excel Цели1. Перейдите в этот документ, чтобы получить нужное значение. Активируйте проект Re 1 и загрузите результаты.

‍

‍

5. Переключитесь в модель cylinder 1m, активируйте проект Re 1e5, загрузите результаты и выведите значения всех целей.

‍

‍

Для сравнения результатов, полученных с помощью FloEFD, с экспериментальной кривой, предпочтительнее выбирать средние значения коэффициента сопротивления. Как в стационарной, так и в нестационарной задаче для средних значений цели менее заметны отклонения.

Результаты сравнения представлены на рисунке ниже.

‍

Таблицы коэффициентов трения на воздухе и в вакууме

03.01.2022 Трибонет

Эскиз Леонардо да Винчи

Содержание

Таблицы коэффициентов трения для твердых смазочных материалов, металлов, пластмасс и антифрикционных материалов

Таблицы коэффициентов трения для различных пар материалов в атмосфере и вакууме приведены ниже. Данные были собраны из различных источников [1,2,3]. См. определение коэффициента трения.

Комбинация материалов Коэффициент трения в воздухе Коэффициент трения в вакууме
Fe-Fe 0,3 1,9
Fe-Mg 1 0,6
Fe-Cd 1,5 0,4
Fe-Pb 0,9 0,4
Нержавеющая сталь — Нержавеющая сталь 0,5 2,9
Нержавеющая сталь – Cu – 0,3
Нержавеющая сталь-алюминий 0,4 0,3
Нержавеющая сталь-Mo – 0,8
Нержавеющая сталь-Ni – 0,8
Нержавеющая сталь-тефлон – 0,2
Нержавеющая сталь-Si – 0,2
Нержавеющая сталь-Ge – 0,2
Нержавеющая сталь-стекло – 0,5
Хромистая сталь – Хромистая сталь 0,5 0,5
Медь-медь 0,5-1,0 4,8-21,0
Медно-никелевый 0,6 1,5-2,0
Аль-Аль 0,8 1,6-2,2
Ал-Ни – 2,4
Al-Cu – 1,5
Ал-Аг – 2,2
Латунь-Латунь 0,4 0,7
Ni-Ni – 4,9
Ag-Ag – 3,9
хром-хром 0,6 3
Золото-Золото 0,6 4,5
Цинк-цинк 1 3
Zr-Zr – 1,5
Хромистая сталь – MoS2 (вакуумное напыление) – 0,06
Хромистая сталь – MoS2 (нанесение трением) – 0,06
Cu-MoS2 0,2 0,07
Латунь-сталь 0,35 –
Шина – Асфальт 0,72 –
Шина – Трава 0,35 –
Алмаз – Алмаз 0,1 –
Стекло – Стекло 0,9-1,0 –
Графит – Сталь 0,1 –
Графит – Графит 0,1 0,5-0,8
Лед — Лед 0,02-0,09 –
Лед – Сталь 0,03 –
Дерево – Дерево >0,2 –
Политетрафторэтилен – политетрафторэтилен 0,04 –

Таблица коэффициентов трения стали

Коэффициент трения дерева, кожи и камня

Таблица коэффициентов трения скольжения для выбранных керамических материалов (комнатная температура на воздухе)

Коэффициент трения льда

В зависимости от давления, температуры и условий образования лед может принимать любую из по меньшей мере восьми аллотропных форм — наибольшее число для любого известного вещества. Эти изменения влияют на поведение коэффициента трения об лед, как показано на рисунке ниже. Рис. 1. Коэффициент трения нержавеющей стали и льда по поликристаллическому льду в зависимости от температуры, [3].

Таблица коэффициентов трения для материалов в режиме фреттинга

При фреттинге коэффициенты трения для одних и тех же пар материалов различаются из-за изменений в механизмах трения. Эти таблицы включают некоторые данные для часто используемых материалов.

Таблица коэффициентов трения в режиме фреттинга в зависимости от влажности

Трибонет

Администрация проекта