Определение коэффициента лобового сопротивления самолета.
Коэффициент лобового сопротивления компоновки самолета, симметричного относительно плоскости X0Z () при углах атакидля самолета с крылом малого удлинения,для самолета с крылом большого удлинения, определяется как сумма коэффициентов лобового сопротивления при нулевой подъемной силе -и индуктивного сопротивления: .
Коэффициент рассчитывается по формуле:
— коэффициенты лобового сопротивления с учетом интерференции фюзеляжа с крылом, горизонтальным и вертикальным оперениями;
-коэффициент, учитывающий дополнительное сопротивление, обусловленное технологическими неровностями поверхности (стыковочные узлы, люки, царапины) , = 0.003 …0.004 ;
К – поправочный коэффициент, уточняющий формулу на неучтенные факторы,
К =1.05 …1.1.
— коэффициент индуктивного сопротивления самолета,
где А – коэффициент отвала поляры,
—
коэффициент подъемной силы самолета.
Определение коэффициента лобового сопротивления фюзеляжа при нулевой подъемной силе.
Коэффициент лобового сопротивления фюзеляжа самолета при нулевой подъемной силе отличается от соответствующего коэффициента изолированного фюзеляжаувеличением донного сопротивления в диапазоне чисел Маха, что учитывается при расчете коэффициента донного сопротивления фюзеляжа
Расчет коэффициента лобового сопротивления изолированного фюзеляжа при нулевой подъемной силе выполняется по соотношению:
где — коэффициент лобового сопротивления трения,
— коэффициент лобового сопротивления давления.
Коэффициент лобового сопротивления трения определяется по формуле:
где — коэффициент сопротивления трения плоской пластины в несжимаемом потоке для полностью турбулентного пограничного слоя,
— число Рейнольдса, рассчитанное по длине фюзеляжа ,
— коэффициент, учитывающий влияние сжимаемости (снимается с графика),
— коэффициент формы, учитывающий отличие фюзеляжа от плоской пластины (снимается с графика),
— площадь омываемой поверхности фюзеляжа (боковой, без площади поверхности донного среза),
—
кинематический коэффициент вязкости,
определяемый по таблице стандартной
атмосферы в зависимости от высоты
полета.
| |
К | 1,05 |
xt | 0,5 |
Fф | 64,45919807 |
Sбокнос | 9,124755862 |
Sбокцил | 47,10346945 |
Sбоккорм | 8,230972752 |
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
2Cf | 0,003 | 0,0024 | 0,0023 | 0,0022 | 0,0021 | |
ημ | 0,98 | 0,96 | 0,95 | 0,9 | 0,82 | 0,8 |
ηλ | 1,08 |
|
|
|
|
|
Cxa0фтр | 0,052861174 | 0,043152 | 0,04099438 | 0,037218582 | 0,032435904 | 0,030206 |
Коэффициент сопротивления давления определяется по формуле:
где
— соответственно коэффициенты сопротивления
носовой и кормовой частей, донного
сопротивления.
Коэффициент сопротивления носовой частиопределяется по графикам в зависимости от числа Маха и.
Коэффициент сопротивления кормовой части фюзеляжа форма обводов кормовой части), определяется по графику Коэффициент сопротивления донного среза при неработающем двигателе определяется для всех значений числаМ по формуле:
,
где – площадь донного среза,- диаметр донного среза,– коэффициент донного давления.
При М< 0.8 ,
— коэффициент, учитывающий влияние удлинения и сужения кормовой части, — коэффициент трения плоской пластины, определяемый по числу.
При М>0.8 определяется по графикам в зависимости от числа Маха, коэффициенттакже снимается по графикам.
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
√(M-1)/λнос | 0,428668942 | 0,3826636 | 0,321501706 | 0,669259171 | 0,801966157 | ё |
(Cханос)при ϕ=1 | 0 | 0 | 0 | 0,104798949 | 0,074651306 | 0,068909 |
Cхакорм | 0,045 | 0,045 | 0,06 | 0,075 | 0,065 | 0,051 |
Коэффициент сопротивления донного среза фюзеляжа:
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
1-ηкорм | 0,21853068 |
|
|
|
|
|
Kη | 0,18 | 0,18 | 0,18 | 0,42 | 0,5 | 0,55 |
Cр дон | -0,3233 | -0,3542 | -0,3615 | -0,28 | -0,27 | -0,2 |
Cxдон | 0,026020793 | 0,0285044 | 0,029092131 | 0,052573439 | 0,060352163 | 0,049176 |
Cxaфдавл | 0,07102079 | 0,073504 | 0,08909213 | 0,23237239 | 0,20000347 |
Cxa0ф | 0,123881967 | 0,1166563 | 0,13008651 | 0,26959097 | 0,232439373 | 0,199291 |
Расчет
коэффициента лобового сопротивления
несущей поверхности (крыла, ГО, ВО) при
нулевой подъемной силе.
Коэффициент лобового сопротивления изолированной несущей поверхности при нулевой подъемной силе определяется по формуле:
где — коэффициент профильного сопротивления, состоящий из сопротивления трения и сопротивления давления, обусловленного перераспределением давления из-за влияния вязкости;- коэффициент волнового сопротивления, обусловленный потерями полного давления (потерями энергии) в скачках уплотнения и перераспределением давления на сверхзвуковых скоростях.
Коэффициент профильного сопротивления:
(4.13)
где — коэффициент, учитывающий долю несущей поверхности= 2.
— коэффициент, учитывающий влияние на профильное сопротивление толщины профиля снимается с графика ,
— коэффициент, учитывающий влияние числа Маха берется с графика.
Коэффициент
трения плоской пластины
(верхняя
и нижняя поверхность) определяется по
графику .
Число Рейнольдса для рассматриваемой несущей поверхности ,- средняя аэродинамическая хорда консольной части несущей поверхности (крыла, ГО, ВО). Как и в случае расчета коэффициента сопротивления трения фюзеляжа, для несущей поверхности принимаем пограничный слой турбулентным. Некоторое завышение коэффициента сопротивления допускается, что определяет запас тяги двигателя.
Крыло
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,00125 | 0,0012 | 0,00115 | 0,0011 | 0,00105 |
Cхар | 0,00304584 | 0,0025382 | 0,002436672 | 0,002335144 | 0,002233616 | 0,002132 |
Вертикальное оперение
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,0015 | 0,0015 | 0,0011 | 0,001 | 0,001 |
Cхар | 0,003046 | 0,00304584 | 0,00304584 | 0,002233616 | 0,002031 | 0,002031 |
Горизонтальное оперение
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,0015 | 0,0015 | 0,0011 | 0,001 | 0,001 |
Cхар | 0,003046 | 0,003046 | 0,003046 | 0,002234 | 0,002031 | 0,002031 |
Коэффициент волнового сопротивления несущей поверхности определяется по соотношению
где
— коэффициент волнового сопротивления
несущей поверхности с ромбовидным
профилем. Зависимостипредставлены на графиках и позволяют
определить коэффициент.
Зависимостипредставлены на графиках и позволяют
определить коэффициент.
Коэффициенты, учитывающие влияние на волновое сопротивление формы профиля крыла бесконечного размаха –К,(так как форма профиля — синусоидальная), конечного размаха крыла — снимается с графика и зависит от .
Для ориентировочной оценки коэффициента волнового сопротивления крыла сложной формы в плане исходное крыло разбивают на 2 вспомогательных простых крыла с постоянной стреловидностью по передней кромкеи площадью в плане. Коэффициент волнового сопротивления рассчитывается по формуле
где — коэффициент волнового сопротивленияn-го вспомогательного простого крыла,
K -коэффициент, учитывающий влияние интерференции на волновое сопротивление крыла. В приближенных расчетах можно принять K = 1.15…1.2.
Коэффициент волнового сопротивления крыла:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,0297216 | 0,02575872 | 0,024343 |
Cxaвл | 0,0297216 | 0,033057024 | 0,025804 |
Коэффициент волнового сопротивления ВО:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,022722812 | 0,016896 | 0,013983 |
Cxaвл | 0,022874297 | 0,021402 | 0,018644 |
Коэффициент волнового сопротивления ГО:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,022723 | 0,016896 | 0,013983 |
Cxaвл | 0,022874 | 0,021402 | 0,018644 |
Сха0 | 0,01704802 | 0,01583 | 0,01726748 | 0,03278182 | 0,02846074 | 0,02463 |
Определение коэффициента индуктивного сопротивления самолета
Коэффициент индуктивного сопротивления самолета определяется соотношением
где А — коэффициент отвала поляры первого рода,
—
коэффициент подъемной силы самолета.
В пределах линейной зависимости коэффициент,
где — производная коэффициента подъемной силы по углу атаки.
Тогда ,
где при заданном значении произведение.
Отвал поляры при отсутствии подсасывающей силы для всех чисел Маха определяется:
, где
| 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
А | 0,39808507 | 0,3763637 | 0,362863317 | 0,469079925 | 0,435848765 | 0,487484 |
Kmax | 6,069390174 | 6,4776973 | 6,316608962 | 4,032088346 | 4,489303768 | 4,562783 |
| M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
α | Сxai |
|
|
|
|
|
|
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
2 |
| 0,003060827 | 0,00323748 | 0,00335793 | 0,002598 | 0,002796 | 0,0025 |
4 |
| 0,012243309 | 0,012949918 | 0,013431721 | 0,01039 | 0,011182 | 0,009998 |
6 |
| 0,027547446 | 0,029137316 | 0,030221371 | 0,023378 | 0,025161 | 0,022496 |
8 |
| 0,048973238 | 0,051799673 | 0,053726883 | 0,041561 | 0,04473 | 0,039992 |
Поверочный расчет аэродинамических характеристик самолета: Учебное пособие, страница 11
Коэффициент лобового сопротивления трения определяется по формуле:
(4. 5)
5)
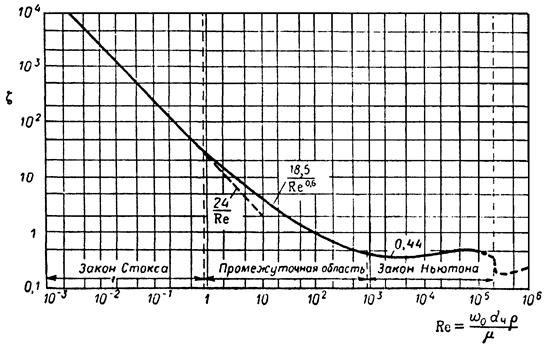
где — коэффициент сопротивления трения плоской пластины в несжимаемом потоке для полностью турбулентного пограничного слоя (рис 4.1),
— число Рейнольдса, рассчитанное по длине фюзеляжа ,
Рис 4.1 Зависимость удвоенного коэффициента трения плоской пластинки от числа Rе и в несжимаемом потоке, — относительная координата точки перехода л.п.с в т.п.с.
Рис 4.2 Зависимость коэффициента трения плоской пластинки от числа М¥
— коэффициент, учитывающий влияние сжимаемости (рис 4.2),
— коэффициент формы, учитывающий отличие фюзеляжа от плоской пластины (рис 4.3), — площадь омываемой поверхности фюзеляжа (боковой, без площади поверхности донного среза),
— кинематический коэффициент вязкости,
определяемый по таблице стандартной атмосферы в зависимости от высоты полета.
Рис 4.3
Коэффициент сопротивления давления определяется по формуле:
где — соответственно коэффициенты сопротивления давления носовой и кормовой частей, донного сопротивления.
Коэффициент сопротивления давления заостренной носовой части определяется по графикам рис. 4.4 а,б для конической и оживальной (в частности параболической) носовых частей. Если носовая часть затуплена, то необходимо учесть сопротивление от затупления. На рис 4.5 а,б приведены примеры конической (а) и оживальной (б) носовых частей, где r – радиус сферического затупления носовой части.
Коэффициент сопротивления конической носовой части с затуплением (рис. 4.5а) рассчитывается по соотношению: (4.7)
где — коэффициент сопротивления исходной, без затупления , конической носовой части (рис. 4.4а)
Рис. 4.4а. График для расчета конической носовой части
Рис. 4.4б. График для расчета носовой части с
параболической образующей
4.4б. График для расчета носовой части с
параболической образующей
Коэффициент сопротивления оживальной (параболической) носовой части с затуплением (рис 4.5б) определяется по соотношению:
(4.8)
где — коэффициент сопротивления исходной, без затупления , оживальной носовой части (рис. 4.4б), , — дополнительный коэффициент сопротивления сферического затупления, определяемый по графику рис. 4.6
Рис 4.5а Рис 4.5б
Рис 4.6
Фюзеляж с воздухозаборником двигателя, рассчитанным на дозвуковые и малые
сверхзвуковые скорости, представляет собой простой диффузор без центрального
конуса. На больших сверхзвуковых скоростях применяют воздухозаборник с
центральным телом. Такой воздухозаборник характеризуют следующие геометрические
параметры: угол полураствора центрального конуса и вынос
конуса относительно обечайки диффузора,
изменяющийся в зависимости от числа Маха набегающего потока (рис. 4.7а).
4.7а).
В общем случае, коэффициент сопротивления носовой части фюзеляжа, выполненной в виде тела вращения с центральным воздухозаборником, представляется в виде:
(4.9)
где площадь входного сечения воздухозаборника,
— площадь миделевого сечения фюзеляжа,
— коэффициент лобового сопротивления носовой части с протоком при j = 1 (рис 4.7б, 4.8) ,
j — коэффициент расхода воздуха,
— коэффициент добавочного сопротивления воздухозаборника, возникающий при j < 1, (рис. 4.10)
— коэффициент подсасывающей силы воздухозаборника, которая теоретически полностью реализуется при определенном закруглении кромок воздухозаборника и криволинейных обводов носовой части фюзеляжа.
Сверхзвуковые самолеты имеют острые кромки воздухозаборника. В этом случае подсасывающая сила на его кромках практически не реализуется.
Современные воздухозаборники проектируются таким образом, что при всех
расчетных режимах работы двигателя j = 1 (рис. 4.7а). Тогда соотношение (4.9) принимает
вид: (4.10)
4.7а). Тогда соотношение (4.9) принимает
вид: (4.10)
Зависимость коэффициента , представлены на графиках рис 4.7б, 4.8.
Между 1900 и 1905 годами братья Райт спроектировали и построили три планеры без двигателя и три самолета с двигателем. При проектировании каждого самолета братья старались максимизировать отношение подъемной силы к лобовому сопротивлению, потому что высокий поднимать и низкий тащить дает лучший самолет производительность. Как они предсказали подъемную силу и сопротивление своей конструкции? Братья Райт были велосипедными механиками и дизайнерами.
и у них было хорошее практическое знание математики и естественных наук. Они знали о
законы Ньютона
движения и о
силы
и
крутящие моменты.
Они написали Смитсоновскому институту, когда начинали свое предприятие в 1899 году. Величина сопротивления, создаваемого объектом, зависит от ряда факторов, включая характеристики воздуха, скорость между объектом и воздух, поверхность над которым циркулирует воздух, форма тела, и склонность тела к потоку, называемая также угол атаки. К тому времени, когда Райты начали свои исследования, было установлено, что
сопротивление зависит от
квадрат скорости
и варьируется линейно с площадью поверхности объекта.
Ранние аэродинамики характеризовали зависимость от свойств воздуха
коэффициентом давления, называемым
коэффициент Смитона, представляющий
сила давления (сопротивления) на плоскую пластину площадью один фут, движущуюся со скоростью одна миля в час через
воздух. где D — сопротивление, k — коэффициент Смитона, V — скорость, A — площадь крыла, cd — коэффициент лобового сопротивления.
Это уравнение несколько отличается от современного
уравнение сопротивления
используется сегодня. Современное уравнение использует
динамическое давление
движущегося воздуха для зависимости от давления, в то время как это уравнение использует
коэффициент Смитона. Современные коэффициенты сопротивления связывают силу сопротивления, действующую на объект, с
сила, создаваемая динамическим давлением, умножается на площадь, а 1900-е
коэффициенты сопротивления связывают силу сопротивления с сопротивлением плоской пластины равной площади.
Для современного уравнения сопротивления коэффициент сопротивления плоской пластины
при движении перпендикулярно потоку 1,28; для уравнения сопротивления 1900-х годов,
коэффициент сопротивления для этой задачи
равно 1,0. Уравнение 1900-х годов предполагает, что вы знаете перпендикулярную силу давления на
подвижная плоская пластина (коэффициент Смитона). Потому что
погрешностей измерения в то время, было много цитируемых значений для
коэффициент в диапазоне от 0,0027 до 0,005. Лилиенталь использовал значение 0,005.
в проектировании и испытании его крыльев.
Когда Райты начали проектировать 1900 самолетов,
они использовали значения коэффициента лобового сопротивления, основанные на работе Лилиенталя.
поэтому они тоже использовали значение 0,005.
Во время кайта и планера
экспериментах 1900 и 1901 годов братья измерили производительность
своего самолета. Ни один из самолетов не показал себя так, как предполагалось.
уравнениями подъемной силы и сопротивления. Самолет 1901 года
был разработан, чтобы поднимать себя (100 фунтов) и пилота (150 фунтов).
при запуске воздушного змея при скорости ветра 15 миль в час и угле атаки 5 градусов.
Но в полете он едва мог подняться при скорости ветра 15 миль в час. Братья также начали сомневаться в точности подъемной силы Лилиенталя.
коэффициенты.
Так что осенью 1901 года они решили определить собственные ценности
для коэффициента лобового сопротивления с помощью
аэродинамическая труба.
Братья построили умный
баланс
непосредственно измерить отношение лобового сопротивления своих моделей к
подъем модели. Они построили еще один
баланс
для определения подъема.
Мы разработали
интерактивный симулятор туннеля
так что вы можете дублировать их результаты в аэродинамической трубе.
в
процесс
испытав множество моделей аэродинамических профилей, братья обнаружили важность
крыла
форма
на коэффициент лобового сопротивления.
Они определили, что данные Лилиенталя были правильными для геометрии крыла.
которые он использовал, но данные не могли быть применены к крылу с очень
разная геометрия. Вы можете просмотреть короткий фильм из «Орвилла и Уилбура Райт», обсуждающих силу сопротивления и как это повлияло на полет их самолетов. Файл фильма может сохранять на свой компьютер и просматривать как подкаст на проигрывателе подкастов. Навигация..
|
Эффекты формы при перетаскивании
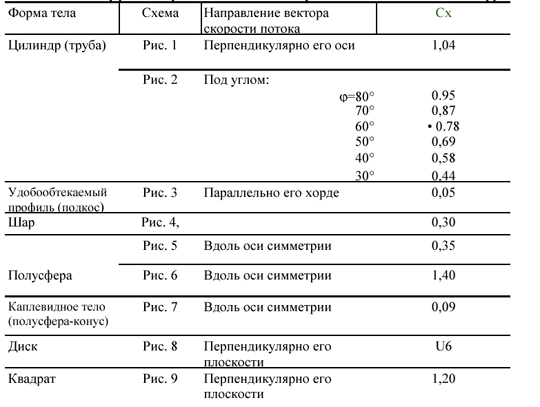
Эффекты формы при перетаскивании Коэффициент аэродинамического сопротивления — это число, которое
аэродинамики используют для моделирования всех сложных зависимостей
перетаскивание по наклону формы,
и некоторые условия течения. Коэффициент лобового сопротивления (Cd) равен лобовому сопротивлению (D), деленному на
количество: плотность (r), умноженная на контрольную площадь (A), умноженная на половину
скорость (V) в квадрате.
Этот слайд показывает
некоторые типичные значения коэффициента лобового сопротивления для различных форм.
Показанные здесь значения были определены экспериментально путем размещения
моделей в аэродинамической трубе и измерения
величина сопротивления и туннельные условия скорости и плотности.
уравнение сопротивления
затем использовался для получения коэффициента. Прогнозируемая фронтальная
площадь каждого объекта использовалась в качестве эталонной площади.
Плоская пластина имеет Cd = 1,28, клиновидная призма с клином обращена
вниз по течению имеет Cd = 1,14, сфера имеет Cd, который варьируется от 0,07 до 0,5,
пуля Cd = 0,295, а типичный аэродинамический профиль Cd = 0,045.
Коэффициент лобового сопротивления (Cd) равен лобовому сопротивлению (D), деленному на
количество: плотность (r), умноженная на контрольную площадь (A), умноженная на половину
скорость (V) в квадрате.
Этот слайд показывает
некоторые типичные значения коэффициента лобового сопротивления для различных форм.
Показанные здесь значения были определены экспериментально путем размещения
моделей в аэродинамической трубе и измерения
величина сопротивления и туннельные условия скорости и плотности.
уравнение сопротивления
затем использовался для получения коэффициента. Прогнозируемая фронтальная
площадь каждого объекта использовалась в качестве эталонной площади.
Плоская пластина имеет Cd = 1,28, клиновидная призма с клином обращена
вниз по течению имеет Cd = 1,14, сфера имеет Cd, который варьируется от 0,07 до 0,5,
пуля Cd = 0,295, а типичный аэродинамический профиль Cd = 0,045.
Мы можем изучить влияние формы на сопротивление, сравнив значения
коэффициента сопротивления для любых двух объектов, пока одна и та же ссылка
используется площадь, а число Маха и число Рейнольдса совпадают. Все коэффициенты лобового сопротивления на этом слайде были получены на низкой скорости.
(дозвуковые) аэродинамические трубы и при аналогичных числах Рейнольдса, за исключением случаев, когда
отмеченный. Быстрое сравнение показывает, что плоская пластина дает самые высокие
сопротивление, а обтекаемый симметричный аэродинамический профиль обеспечивает наименьшее сопротивление на
коэффициент почти 30! Форма очень сильно влияет на количество
произведено сопротивление. Коэффициент аэродинамического сопротивления для сферы дан с
диапазон значений, потому что сопротивление сферы сильно зависит от
Число Рейнольдса. (Поток мимо сферы или цилиндра проходит через
число переходов со скоростью. На очень низкой скорости стабильно
с подветренной стороны образуется пара вихрей. Как скорость
возрастает, вихри становятся неустойчивыми и попеременно сбрасываются
вниз по течению. При еще большем увеличении скорости
пограничный слой
переходы к хаотическому турбулентному течению с вихрями множества различных
чешуя сбрасывается турбулентным следом от тела.
Все коэффициенты лобового сопротивления на этом слайде были получены на низкой скорости.
(дозвуковые) аэродинамические трубы и при аналогичных числах Рейнольдса, за исключением случаев, когда
отмеченный. Быстрое сравнение показывает, что плоская пластина дает самые высокие
сопротивление, а обтекаемый симметричный аэродинамический профиль обеспечивает наименьшее сопротивление на
коэффициент почти 30! Форма очень сильно влияет на количество
произведено сопротивление. Коэффициент аэродинамического сопротивления для сферы дан с
диапазон значений, потому что сопротивление сферы сильно зависит от
Число Рейнольдса. (Поток мимо сферы или цилиндра проходит через
число переходов со скоростью. На очень низкой скорости стабильно
с подветренной стороны образуется пара вихрей. Как скорость
возрастает, вихри становятся неустойчивыми и попеременно сбрасываются
вниз по течению. При еще большем увеличении скорости
пограничный слой
переходы к хаотическому турбулентному течению с вихрями множества различных
чешуя сбрасывается турбулентным следом от тела.

 и получил технические документы, описывающие авиационную
теории дня. Имелись математические уравнения, которые могли
использовать для прогнозирования количества
поднимать
и перетащите
который будет генерировать объект.
уравнение сопротивления показано на этом слайде.
и получил технические документы, описывающие авиационную
теории дня. Имелись математические уравнения, которые могли
использовать для прогнозирования количества
поднимать
и перетащите
который будет генерировать объект.
уравнение сопротивления показано на этом слайде.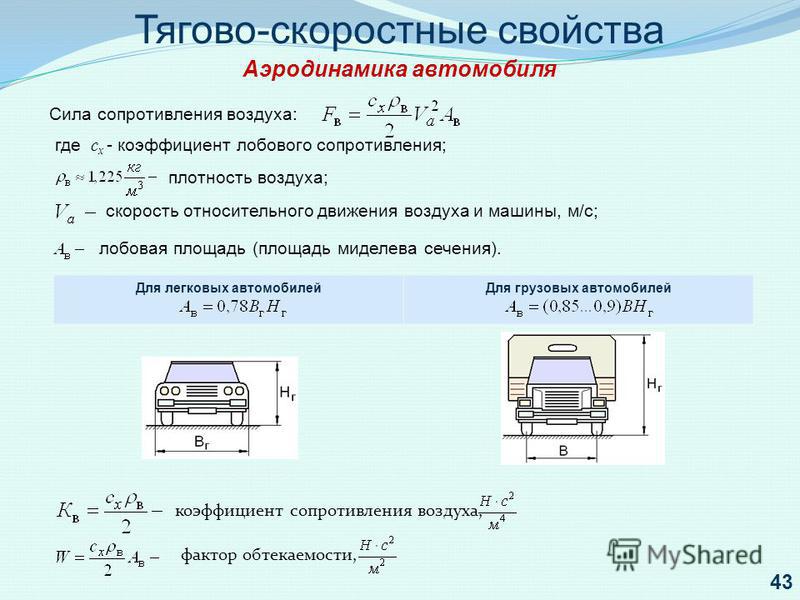 Они считали, что любой объект, движущийся по воздуху, преобразует некоторые
часть силы давления в сопротивление, и они представляли эту часть
коэффициент сопротивления. Полученное уравнение имеет вид:
92 * А * кд
Они считали, что любой объект, движущийся по воздуху, преобразует некоторые
часть силы давления в сопротивление, и они представляли эту часть
коэффициент сопротивления. Полученное уравнение имеет вид:
92 * А * кд
 гораздо больший угол атаки.
Поэтому братья начали сомневаться в значении коэффициента Смитона 0,005 и
они определили, что значение 0,0033 более точно соответствует их данным.
Современное принятое значение составляет 0,00326.
гораздо больший угол атаки.
Поэтому братья начали сомневаться в значении коэффициента Смитона 0,005 и
они определили, что значение 0,0033 более точно соответствует их данным.
Современное принятое значение составляет 0,00326. Крылья Лилиенталя имели довольно короткий размах и эллиптическую форму.
форма в плане, в то время как братья использовали длинную, тонкую, прямоугольную форму в плане.
Братья протестировали более пятидесяти различных
модели
определить
как подъемная сила и лобовое сопротивление зависят от различных параметров конструкции
и они использовали эти данные для разработки своих 1902 самолета
используя уравнение сопротивления, показанное на слайде, со своими собственными коэффициентами сопротивления.
Братья определили требования к мощности для самолета 1903 года.
на основе их данных о перетаскивании.
Крылья Лилиенталя имели довольно короткий размах и эллиптическую форму.
форма в плане, в то время как братья использовали длинную, тонкую, прямоугольную форму в плане.
Братья протестировали более пятидесяти различных
модели
определить
как подъемная сила и лобовое сопротивление зависят от различных параметров конструкции
и они использовали эти данные для разработки своих 1902 самолета
используя уравнение сопротивления, показанное на слайде, со своими собственными коэффициентами сопротивления.
Братья определили требования к мощности для самолета 1903 года.
на основе их данных о перетаскивании.