8 Расчет крутящих моментов на валах

8.1 Расчет крутящего момента на валу электродвигателя

Для определения крутящего момента на валу электродвигателя привода главного движения используется номинальная мощность и номинальная частота вращения:

где – мощность электродвигателя, кВт:

–номинальная частота вращения электродвигателя, мин^-1:

.

.

8.2 Расчет крутящего момента на валах привода

Крутящий момент на валах привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до соответствующего вала;

–расчетная частота вращения соответствующего вала, принимается по графику частот, мин^-1.

8.3 Расчет крутящего момента на первом валу привода

Крутящий момент на первом валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 1-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин^-1: = 2850 мин^-1.

КПД участка привода до первого вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

8.4 Расчет крутящего момента на втором валу привода

Крутящий момент на втором валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 2-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин

-1: = 630 мин^-1.

КПД участка привода до второго вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

— КПД зацепления зубчатых колес; .

8. 5 Расчет крутящего момента на третьем валу привода

Крутящий момент на третьем валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 3-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин^-1: = 160 мин

-1.

КПД участка привода до третьего вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

— КПД зацепления зубчатых колес; .

8.6 Расчет крутящего момента на четвертом валу привода

Крутящий момент на четвертом валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 4-го вала;

–расчетная частота вращения на 4-ом валу, определяется по формуле:

где – минимальная частота вращения четвертого вала, мин^-1:

мин^-1;

–максимальная частота вращения четвертого вала, мин^-1:

мин^-1.

КПД участка привода до четвертого вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

–КПД зацепления зубчатых колес; .

Крутящий момент на шпинделе рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до шпинделя;

–расчетная частота вращения шпинделя, определяется по формуле:

где – минимальная частота вращения четвертого вала, мин^-1:

мин^-1;

–диапазон регулирования частот вращения шпинделя:

КПД участка привода до шпинделя рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

–КПД зацепления зубчатых колес; .

9 Проектный расчет передач

9.1 Расчет цилиндрической прямозубой постоянной передачиz₁–z₂

9.1.1 Исходные данные

1. Расчетный крутящий момент на первом валу привода, H·м:

Т₁ = 13 Н·м;

2. Число зубьев шестерни: z₁ = 18;

3. Число зубьев колеса: z₂ = 83;

4. Передаточное число передачи: u₁ = 4,76.

9.1.2 Выбор материала и термической обработки зубчатых

колес

В качестве материала для зубчатых колес передачи выбираем сталь 40Х, которая отвечает необходимым техническим и эксплуатационным требованиям. В качестве термической обработки выбираем объемную закалку, позволяющую получить твердость зубьев 40..50HRC_э.

9.1.3 Проектный расчет постоянной прямозубой зубчатой передачи на контактную выносливость

Диаметр начальной окружности шестерни рассчитывается по формуле:

где вспомогательный коэффициент: для прямозубых передач

— расчётный крутящий момент на первом валу, Н·м: Т₁=13 Н·м;

коэффициент нагрузки для шестерни, равный 1,3. .1,5: принимаем

— передаточное число:

отношение рабочей ширины венца передачи к начальному диаметру шестерни:

допускаемое контактное напряжение, МПа.

Допускаемое контактное напряжение для прямозубых передач рассчитывается по формуле:

где базовый предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений, МПа;

МПа;

S_H – коэффициент безопасности: S_H = 1,1.

Коэффициент отношения рабочей ширины венца передачи к начальному диаметру шестерни может приниматься в пределах

или определяется по формуле:

отношение рабочей ширины венца передачи к модулю: принимаем

число зубьев шестерни: z₁ = 18.

что находится в допустимых пределах .

Таким образом, диаметр начальной окружности шестерни равен:

Модуль постоянной прямозубой передачи определяется из условия расчета на контактную выносливость зубьев по рассчитанному значению диаметра начальной окружности шестерни по формуле:

где диаметр начальной окружности шестерни, мм:d_w1 = 38,75 мм;

число зубьев шестерни: z₁ = 18.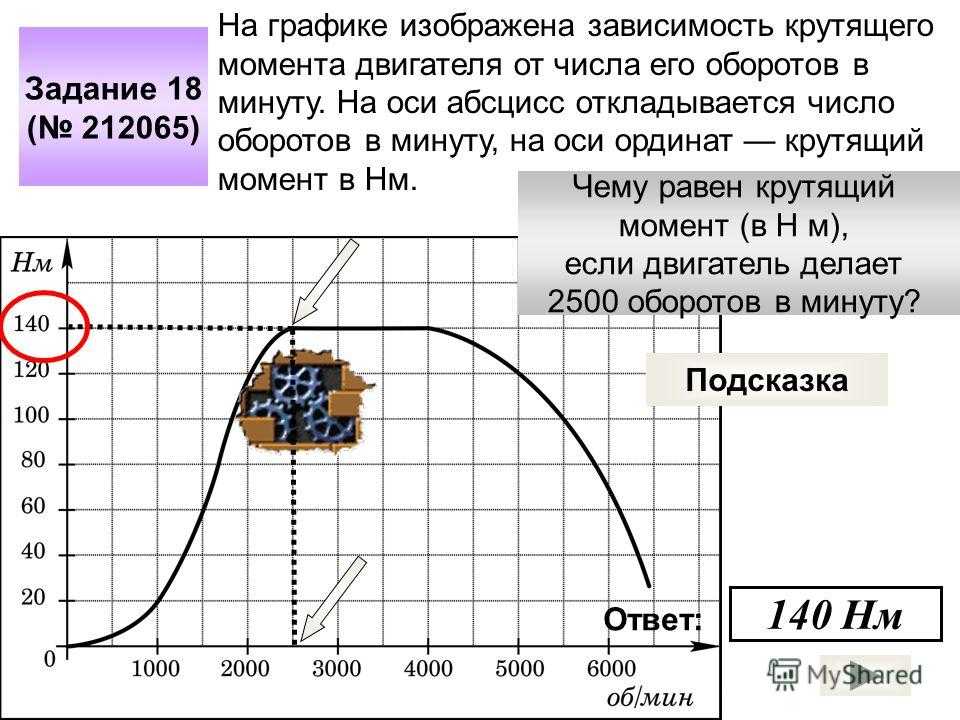

Как определить крутящий момент в балке

При расчете сборных или монолитных железобетонных балок (ригелей) всегда нужно внимательно относиться к крутящему моменту. Очень часто расчет на кручение требует увеличить сечение или армирование балки. Сечение балки при кручении эффективней увеличивать в ширину (увеличение балки по высоте дает малый эффект), оптимально при кручении уходить от прямоугольного сечения к квадратному.

В каких ситуациях в балке возникает крутящий момент?

1) Если на балку опирается перекрытие только с одной стороны – оно своим весом пытается крутить балку в сторону пролета перекрытия.

2) Если на балку опирается перекрытие с двух сторон, но пролет этих перекрытий разный – тогда нагрузка от перекрытия с большим пролетом перевешивает в свою сторону и крутит балку.

3) Если на балку опирается перекрытие равных пролетов, но нагрузки на этих перекрытиях отличаются (разное назначение помещений, наличие оборудования на перекрытии и т. п.) – тогда балка также прокручивается в сторону большей нагрузки.

4) Если вдоль балки действует вертикальная нагрузка (например, от веса перегородки), сбитая в сторону от оси балки.

Рассмотрим определение крутящего момента на примерах.

Пример 1. Монолитное балочное перекрытие. Необходимо определить крутящий момент в крайней балке. Суммарная нагрузка от веса монолитного перекрытия и всех нагрузок на нем равна: qн = 675 кг/м² (нормативная) и qр =775 кг/м² (расчетная).

Расчет ведется на 1 погонный метр балки.

В монолитном перекрытии связь перекрытия с балками жесткая. При такой схеме расчетный пролет перекрытия равен пролету плиты в свету между балками L₀ = 2,8 м, а нагрузка от плиты на балку передается в месте примыкания балки к перекрытию.

Найдем нагрузку на 1 п.м балки от половины пролета плиты 2,8/2 = 1,4 м:

Рн = 675∙1,4 = 945 кг/м;

Рр = 775∙1,4 = 1085 кг/м.

Крутящий момент в балке рассчитывается умножением вертикальной нагрузки на эксцентриситет – расстояние от оси приложения этой нагрузки до оси, проходящей через центр тяжести балки. В нашем случае эксцентриситет равен половине ширины балки, т.е. 100 мм = 0,1 м.

Итак, определяем крутящий момент в балке (на 1 п.м балки):

Мн = 945∙0,1 = 94,5 кг∙м/м;

Мр = 1085∙0,1 = 108,5 кг∙м/м.

Пример 2. Сборное перекрытие опирается на балку с двух сторон. С одной стороны пролет перекрытия 6 м и есть пригруз в виде перегородки, опирающейся параллельно балке; с другой стороны пролет перекрытия 3,6 м. Нагрузка от перегородки  0,65 т/м, расстояние от оси балки до перегородки 1,5 м. Нагрузка от собственного веса перекрытия 0,3 т/м². Нагрузка на перекрытии: постоянная 0,1 т/м²; временная 0,3 т/м². Ширина балки 0,3 м. Глубина опирания плит перекрытия на балку 0,14 м.

Расчет ведется на 1 п.м балки.

Определим расчетный пролет каждого перекрытия и найдем точку приложения нагрузки от перекрытия на балку.

Плита опирается на балку на 140 мм. Нагрузка от плиты на этой площади распределена не равномерно, а по треугольнику. Максимально плита давит со стороны пролета (с края балки), а к краю плиты нагрузка сходит к нулю. Чтобы привести эту распределенную нагрузку к сосредоточенной, нужно принять ось приложения этой сосредоточенной нагрузки – в центре тяжести треугольника, на расстоянии 1/3 от края балки. У нас получается, что расстояние от края балки до сосредоточенной нагрузки 140/3 = 47 мм, а расстояние от этой нагрузки до оси, проходящей через центр тяжести балки 150 – 47 = 103 мм. Расстояние между сосредоточенными нагрузками равно расчетному пролету плиты L₀, который для наших плит будет равен:

— для плиты 6 м: L₀ = 6000 – 2∙103 = 5794 мм;

— для плиты 3,6 м: L₀ = 3600 – 2∙103 = 3394 мм.

Построим эпюры поперечных сил для наших плит.

Равномерно-распределенная нагрузка на 1 погонный метр плиты равна:

— нормативная qн = 1∙(0,3 + 0,1 + 0,3) = 0,7 т/м;

— расчетная qр = 1∙(1,1∙0,3 + 1,1∙0,1 + 1,2∙0,3) = 0,8 т/м.

Сосредоточенная нагрузка от перегородки на плите Nн = 0,65 т/м (нормативная) и Nр = 1,1∙0,65 = 0,72 т/м (расчетная) находится на расстоянии 1500 мм от оси балки и на расстоянии 1500 – 103 = 1397 мм от принятой нами точки опоры плиты, через которую проходит ось передачи вертикальной нагрузки на балку.

Схема для нормативных нагрузок будет следующая (так как плиты опираются шарнирно, то каждую из них нужно посчитать по отдельной схеме):

Левая плита разбита на два участка: 1-2 и 2-3, правая плита представляет собой один участок 4-5.

В правой плите мы сразу можем найти значения поперечной силы:

Q = 0,5∙qL₀ = 0,5∙0,65∙3,394 = 1,1 т.

Построим эпюру для правой плиты:

Значение поперечной силы на опоре (в точке 4) равно искомой нагрузке, которую плита передает на балку: Р₄= 1,1 т (направлена вниз).

Теперь разберемся с эпюрой для левой плиты. Так как помимо распределенной нагрузки у нас есть сосредоточенная сила, у нас будет несколько больше операций.

Для удобства расчета левой плиты заменим равномерно распределенную нагрузку q равнодействующей силой N:

N_1-2 = 0.65∙4,397 = 2,86 т;

N_2-3 = 0,65∙1,397 = 0,91 т.

Зная, что в шарнирно-опирающейся плите моменты на опоре равны нулю, составим уравнение равновесия, чтобы найти реакции на опоре.

ΣМ₁ = 0:

2,86∙2,199 + 0,65∙4,397 + 0,91∙5,096 – R₃∙5,794 = 0, откуда найдем реакцию:

R₃ = -13.78/5,794 = 2,38 т.

ΣМ₃ = 0:

0,91∙0,698 + 0,65∙1,397 + 2,86∙3,595 – R₁∙5,794 = 0, откуда найдем реакцию:

R₁ = 11,82/5,794 = 2,04 т.

Строить эпюру поперечных сил в плите для определения крутящего момента в балке нам не нужно, т.к. найденная нами реакция на опоре R₃ равна максимальной поперечной силе и равна нагрузке, передаваемой плитой на балку: Р₃= 2,38 т (направлена вниз).

Теперь у нас есть все исходные данные для определения крутящего момента.

Определим нормативный крутящий момент путем умножения сил на плечо. Принимаем силу, вращающую балку против часовой стрелки со знаком «+», а по часовой – со знаком «-«:

Мн = 2,38∙0,103 – 1,1∙0,103 = 0,13 т∙м/м – нормативный крутящий момент, приходящийся на 1 п.м балки.

Расчетный крутящий момент находится точно так же.

Пример 3. Вдоль балки расположена перегородка, которая сбита относительно оси балки на 150 мм. Перекрытие опирается на балку с двух сторон, пролеты перекрытия и нагрузки – одинаковые. Толщина перегородки 0,12 м, материал кирпич (1,8 т/м³), высота 3 м.

Расчет ведем на 1 погонный метр балки.

Определим вертикальную нагрузку от перегородки:

0,12∙3∙1,8 = 0,65 т/м – нормативная нагрузка;

1,1∙0,65 = 0,72 т/м – расчетная нагрузка.

Определим крутящий момент в балке путем умножения силы на плечо:

Мн = 0,65∙0,15 = 0,1 т∙м/м;

Мр = 0,72∙0,15 = 0,11 т∙м/м.

Как рассчитать крутящий момент для затяжки болтов

Вы должны знать, как рассчитать крутящий момент для затяжки болтов, чтобы убедиться, что ваше приложение работает исправно и безопасно. Ошибки в расчете крутящего момента могут привести к дорогостоящему отказу, включая затраты времени и хлопот на замену сломанного оборудования.

Что такое крутящий момент?

Крутящий момент – это сила кручения, измеряющая силу, умноженную на расстояние. Это приложение силы, действующей на радиальном расстоянии, для создания натяжения в резьбовых соединениях. Когда гайка и болт затягиваются, резьба преобразует приложенный крутящий момент в натяжение, которое преобразуется в усилие зажима. В Соединенных Штатах он измеряется в футо-фунтах, и мы указали размеры каждого из наших продуктов на их странице продукта.

Почему важен момент затяжки болтов?

Вы должны убедиться, что ваше приложение имеет соответствующий крутящий момент и натяжение, чтобы избежать срезания болтов (раздвижения) и растяжения (растягивания). После того, как гайка накручена на болт, дополнительный крутящий момент заставляет гайку поворачиваться и растягивать болт. Когда болт растягивается, он становится прочной пружиной, которая сжимает компоненты вместе. Компоненты не будут разорваны, если растягивающая нагрузка не превысит зажимную нагрузку. При сдвигающих нагрузках повышенное трение предотвращает относительное движение компонентов, предотвращая разрушение материала.

Определение подходящей величины крутящего момента зависит от свойств металла болта и назначения болта. По сути, вам нужно убедиться, что у вас есть подходящие материалы для вашего приложения. Использование неправильных материалов или неправильный расчет крутящего момента может быть потенциально опасным. Недостаточно затянутый болт деформируется и не сможет обеспечить необходимое прижимное усилие, а перетянутый болт сломается.

Как рассчитать крутящий момент

Чтобы определить расчетное значение крутящего момента, используйте стандартную формулу крутящего момента:

T = DFK

Эта формула выражает зависимость между нагрузкой на болт и приложенным крутящим моментом. «D» представляет диаметр болта, «F» — осевое усилие болта, а «K» представляет «k-фактор» или «коэффициент гайки», который зависит от использования или отсутствия смазки. Коэффициент k для соединения без смазки составляет 0,2. Соединения без смазки обычно называют «сухими», а процесс затяжки соединения известен как «сухая затяжка». К-фактор смазываемого соединения обычно составляет от 0,15 до 0,18.

Несмазываемое или сухое соединение имеет большее трение между компонентами, что требует приложения большего крутящего момента для достижения того же прогиба/хода, что и в смазываемом соединении. Эти факторы лучше всего определяются после большого количества экспериментов посредством всестороннего тестирования.

Пример расчета крутящего момента болта

В этом примере наш K будет равен 0,2 для соединения без смазки. Диаметр нашего болта будет 0,5 дюйма, а осевое усилие болта будет 11 175 фунтов:

T = 0,2 x 0,5 x 11 175

T = 1 117,5 дюймово-фунтов.

Затем преобразуйте в футо-фунты путем деления на 12:

T = 1117,5 / 12

T = 93,125 футо-фунтов

Наше значение T в этом уравнении равно примерно 93 футо-фунтам.

Использование динамометрического ключа для расчета крутящего момента

Динамометрические ключи — это точные инструменты, которые позволят вам измерять и применять нужный крутящий момент для получения необходимых результатов. Динамометрические ключи рассчитывают величину крутящего момента в аналоговом или цифровом формате. При расчете крутящего момента всегда помните, что динамометрические ключи не обладают идеальной точностью. Если вы предпочитаете, свяжитесь с нами по поводу оптимального крутящего момента для различных комбинаций диаметра болта, типа резьбы и марки или класса.

Как проверить расчет крутящего момента

После расчета крутящего момента обязательно дважды проверьте правильность расчета, чтобы обеспечить безопасность и надлежащее функционирование вашего оборудования. Небольшая ошибка может привести к большому расхождению в вашей окончательной цифре. Чтобы проверить правильность расчета крутящего момента, используйте следующие три проверенных метода:

Проверка первого движения

После того, как вы затянули крепежный элемент, с помощью ключа для проверки крутящего момента медленно прилагайте усилие в направлении затяжки, пока не заметите первое движение крепежного элемента. . Показание является надежным показателем первоначально приложенного крутящего момента. Это наиболее надежный показатель крутящего момента после затяжки.

Тест на ослабление

Это то же самое, что и первый метод, только в обратном направлении. Момент, когда вы почувствуете первое ослабляющее движение, создаст хорошие показания на вашем ревизионном ключе.

Тест на маркировку

Отметьте поверхность крепежного элемента после затяжки болта или гайки и продолжайте эту метку до поверхности, к которой он крепится. Теперь ослабьте застежку, подождите немного и снова затяните, пока отметки, которые вы только что сделали, не совместятся. Крутящий момент, необходимый для достижения этой точки, является хорошей ссылкой на исходный используемый крутящий момент.

Вопросы?

Если у вас есть вопросы о том, как рассчитать момент затяжки болтов для вашего приложения, заполните контактную форму внизу этой страницы или позвоните нам по телефону 440.721.8350.

Как рассчитать чистый крутящий момент

Обновлено 28 декабря 2020 г.

Автор: Липи Гупта

Представьте себе: вам нужно выкрутить болт из деревянной доски. Вы находите ключ нужного размера и закрепляете его на болте. Для того, чтобы начать ослаблять гаечный ключ, вам нужно держать ручку и тянуть или толкать в направлении, которое перпендикулярно ручке ключа. Нажатие в направлении ключа не приведет к крутящему моменту болта, и он не ослабнет.

Крутящий момент — это влияние, вычисляемое из сил, которые вызывают вращательное движение или вызывают вращение вокруг оси.

Общие физики крутящего момента

Формула для определения крутящего момента, τ IS

\ TAU = R \ Times F

, где R — это широкое подразделение. и F — сила. Помните, r , τ , и F — все векторные величины, поэтому операция представляет собой не скалярное умножение, а векторное перекрестное произведение. n_i r_i F_i sin(\theta)

Как и в кинематике, если сумма крутящих моментов равна 0, то объект находится в равновесии вращения, то есть не ускоряется и не замедляется.

Словарь по физике крутящего момента

Уравнение крутящего момента содержит важную информацию о том, как создается крутящий момент и как рассчитать чистый крутящий момент. Понимание терминов в уравнении поможет вам выполнить общий расчет полезного крутящего момента.

Во-первых, ось вращения — это точка, вокруг которой будет происходить вращение. В примере с крутящим моментом ключа ось вращения проходила через центр болта, поскольку ключ будет вращаться вокруг болта. Для качелей осью вращения является середина скамьи, где находится точка опоры, а дети на концах качелей прикладывают крутящий момент.

Далее расстояние между осью вращения и приложенной силой называется плечом рычага. Определение плеча рычага может оказаться сложной задачей, потому что это векторная величина, поэтому потенциально может быть много возможных плеч рычага, но только одно правильное.

Наконец, линия действия представляет собой воображаемую линию, которую можно провести от приложенной силы, чтобы определить плечо рычага.

Пример расчета крутящего момента

Лучший способ приступить к решению большинства физических задач — нарисовать картину ситуации. Иногда это изображение описывается как диаграмма свободного тела (FBD), где объект, на который действуют силы, нарисован, а силы нарисованы в виде стрелок с указанием их направления и величины. Другая важная информация, которую нужно добавить в FBD, — это оси координат и ось вращения.

Для расчета полезного крутящего момента крайне важна точная диаграмма свободного тела.

Шаг 1: Начертите FBD и включите оси координат. Обозначьте ось вращения.

Шаг 2: Изобразите все силы, действующие на тело, используя предоставленную информацию, чтобы точно расположить силы относительно оси вращения.

Шаг 3: Чтобы определить плечо рычага (которое, вероятно, указано в задаче), продлите линию действия силы так, чтобы плечо рычага можно было провести через ось вращения и перпендикулярно силе.