ПДД – Перевозка грузов

08.04.2014

23.1. Масса перевозимого груза и распределение нагрузки по осям не должны превышать величин, установленных предприятием-изготовителем для данного транспортного средства.

23.2. Перед началом и во время движения водитель обязан контролировать размещение, крепление и состояние груза во избежание его падения, создания помех для движения.

23.3. Перевозка груза допускается при условии, что он:

не ограничивает водителю обзор;
не затрудняет управление и не нарушает устойчивость транспортного средства;
не закрывает внешние световые приборы и световозвращатели, регистрационные и опознавательные знаки, а также не препятствует восприятию сигналов, подаваемых рукой;
не оздает шум, не пылит, не загрязняет дорогу и окружающую среду.

Если состояние и размещение груза не удовлетворяют указанным требованиям, водитель обязан принять меры к устранению нарушений перечисленных правил перевозки либо прекратить дальнейшее движение.

Номер закрыт велосипедом или грузом

23.4. Груз, выступающий за габариты транспортного средства спереди и сзади более чем на 1 м или сбоку более чем на 0,4 м от внешнего края габаритного огня, должен быть обозначен опознавательными знаками «Крупногабаритный груз», а в темное время суток и в условиях недостаточной видимости, кроме того, спереди — фонарем или световозвращателем белого цвета, сзади — фонарем или световозвращателем красного цвета.

23.5. Перевозка тяжеловесных и опасных грузов, движение транспортного средства, габаритные параметры которого с грузом или без него превышают по ширине 2,55 м (2,6 м — для рефрижераторов и изотермических кузовов), по высоте 4 м от поверхности проезжей части, по длине (включая один прицеп) 20 м, либо движение транспортного средства с грузом, выступающим за заднюю точку габарита транспортного средства более чем на 2 м, а также движение автопоездов с двумя и более прицепами осуществляются в соответствии со специальными правилами.

Международные автомобильные перевозки осуществляются в соответствии с требованиями к транспортным средствам и правилами перевозки, установленными международными договорами Российской Федерации.

Перейти к следующему разделу ПДД:

• Общие положения
• Общие обязанности водителей
• Применение специальных сигналов
• Обязанности пешеходов
• Обязанности пассажиров
• Сигналы светофора и регулировщика
• Применение аварийной сигнализации и знака аварийной остановки
• Начало движения, маневрирование
• Расположение транспортных средств на проезжей части
• Скорость движения
• Обгон, опережение, встречный разъезд
• Остановка и стоянка
• Проезд перекрестков
• Пешеходные переходы и места остановок маршрутных транспортных средств
• Движение через железнодорожные пути
• Движение по автомагистралям
• Движение в жилых зонах
• Приоритет маршрутных транспортных средств
• Пользование внешними световыми приборами и звуковыми сигналами
• Буксировка механических транспортных средств
• Учебная езда
• Перевозка людей
• Перевозка грузов
• Дополнительные требования к движению велосипедистов и водителей мопедов
• Дополнительные требования к движению гужевых повозок, а также к прогону животных
• Приложение 1 Дорожные знаки (по ГОСТу Р 52289-2004 и ГОСТу Р 52290-2004)
• Приложение 2 Дорожная разметка и её характеристики
• Основные положения по допуски транспортных средств к эксплуатации и обязанности должностных лиц по обеспечению безопасности дорожного движения
• Приложение Перечень неисправностей и условий, при которых запрещается эксплуатация транспортных средств

Длина Ширина Высота Определения и Примеры

Введение

Длина, ширина и высота – это три измерения материи.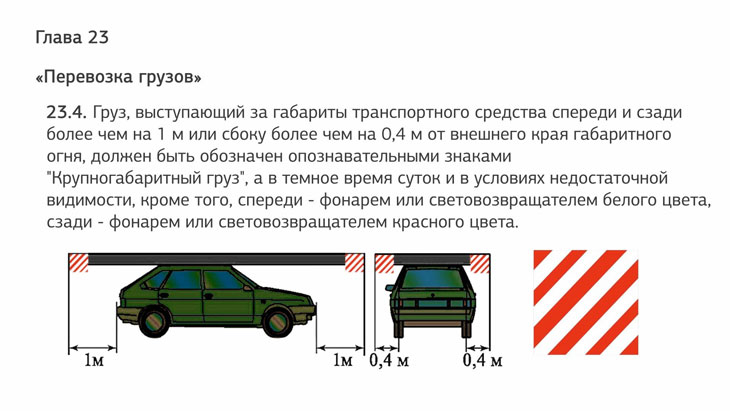 Но что именно означают эти термины? И как мы можем использовать их в повседневной жизни? В этом сообщении блога мы рассмотрим определения длины, ширины и высоты. Мы также приведем примеры того, как использовать эти измерения в реальных сценариях. К концу этого поста вы должны лучше понять, что влечет за собой каждое измерение и как применить его в своей жизни.

Что такое Длина Ширина Высота?

Длина, ширина и высота — это три измерения объекта. Они измеряются в таких единицах, как дюймы или сантиметры.

Длина — это расстояние от одного конца объекта до другого. Это самое длинное измерение.

Ширина — это расстояние от одной стороны объекта до другой. Это самое короткое измерение.

Высота — это расстояние от верха объекта до низа.

Длина против ширины

Когда дело доходит до описания размера объекта, длина, ширина и высота являются тремя наиболее часто используемыми мерами. Длина — это мера длины объекта от одного конца до другого, а ширина — это мера ширины объекта из стороны в сторону. Высота — это мера высоты объекта сверху вниз.

С точки зрения математики, длина — это всегда самая длинная сторона объекта, а ширина и высота — это два других измерения, которые завершают трехмерную форму. Когда даны все три меры, это называется анализом размерностей. Например, коробку можно описать как 10 сантиметров в длину, 5 сантиметров в ширину и 2 сантиметра в высоту.

Важно отметить, что когда мы говорим о длине чего-либо, мы имеем в виду его самое длинное измерение. Например, лист бумаги может иметь длину 8,5 дюймов, но его ширина будет намного меньше — всего 11 дюймов. То же самое касается высоты — здание может быть высотой в сотни футов, но его длина и ширина будут намного больше, чем просто его высота.

Длина x Ширина x Высота

Когда вы видите размеры объекта, указанные как «длина x ширина x высота», это относится к измерению этого объекта в трехмерном пространстве. Длина всегда самая длинная сторона, ширина всегда средняя сторона, а высота всегда самая короткая сторона. Вы можете думать об этом так: если бы вы разрезали прямоугольную коробку по швам, длина была бы открытой стороной, ширина была бы плоской стороной, которая была разрезана, а высота была бы толщиной коробка.

Вот несколько примеров того, как найти размеры обычных объектов:

Стандартный лист бумаги имеет длину 8,5 дюймов и ширину 11 дюймов. Чтобы найти его высоту, нам нужно знать его толщину. Допустим, лист бумаги имеет толщину 0,1 дюйма. Это означает, что его размеры составляют 8,5 дюйма x 11 дюймов x 0,1 дюйма.

Кредитная карта имеет длину 3,370 дюйма и ширину 2,125 дюйма. Его высоту можно оценить по толщине, которая обычно составляет около 0,030 дюйма. Таким образом, размеры кредитной карты составляют 3,370 дюйма x 2,125 дюйма x 0,030 дюйма 9.0007

Длина Ширина Высота коробки

Когда дело доходит до измерения длины, ширины и высоты коробки, это можно сделать несколькими способами. Во-первых, вы можете использовать линейку или измерительную ленту, чтобы измерить размеры снаружи коробки. Это наиболее распространенный способ измерения размера коробки.

Другой способ измерить длину, ширину и высоту коробки — использовать процесс, называемый обклеиванием лентой. Здесь вы берете кусок ленты и отмечаете каждую сторону коробки в ее самой длинной точке, а затем измеряете расстояние между двумя отметками с помощью линейки или рулетки.

Последний способ измерить длину, ширину и высоту коробки — использовать объем. Это делается путем умножения длины на ширину и на высоту (Д х Ш х В). Это даст вам общий объем коробки в кубических дюймах или кубических сантиметрах.

Теперь, когда вы знаете, как измерить длину, ширину и высоту коробки, давайте рассмотрим несколько примеров:

Пример 1. Прямоугольная коробка в форме призмы размером 5 дюймов в длину, 4 дюйма в ширину и 3 дюйма в высоту общий объем 60 кубических дюймов (5 х 4 х 3 = 60).

Пример 2. Коробка в форме куба со сторонами 6 дюймов имеет общий объем 216 кубических дюймов (6 x 6 x 6 = 216).

Заключение

Мы надеемся, что эта статья об определениях и примерах длины, ширины и высоты оказалась для вас полезной. Помните, что при работе с объектами в реальном мире важно учитывать тот факт, что они часто не имеют идеальной геометрической формы. Однако понимание основных концепций этих трех измерений является отличной отправной точкой для всех, кто хочет больше узнать о геометрии и пространственных отношениях.

Длина Ширина Высота – Формула, Примеры

длина, ширина и высота – это размеры геометрической фигуры, которые показывают длину, ширину и высоту фигуры. В то время как длина — самая длинная сторона фигуры, ширина — более короткая сторона, а высота — вертикальный размер фигуры. Давайте узнаем больше о длине, ширине, высоте фигур.

1.	Что такое Длина Ширина Высота?
2.	Длина против ширины
3.	Длина Ширина Высота коробки
4.	Часто задаваемые вопросы о длине, ширине, высоте

Что такое Длина Ширина Высота?

Длина, ширина и высота — это инструменты, которые используются для определения размеров объекта. Когда мы говорим о двухмерных фигурах (2D-фигурах), мы используем длину и ширину, тогда как, когда мы ссылаемся на трехмерные фигуры (3D-фигуры), мы используем высоту вместе с длиной и шириной. Давайте теперь разберемся с тремя терминами.

• Длина: длина используется для измерения расстояния между двумя точками. Длина — это самое длинное измерение фигуры, и она показывает, насколько длинна данный объект или фигура. Он выражается в линейных единицах, таких как метры, сантиметры, дюймы и так далее.
• Ширина: Ширина — это более короткое расстояние объекта или фигуры, и она показывает, насколько широка данная фигура. Ширина также выражается в линейных единицах, таких как метры, сантиметры, дюймы и т.
  д.
• Высота или глубина: высота объекта относится к его глубине или третьему вертикальному измерению объекта и показывает, насколько высок или глубок объект. Высота или глубина объекта выражается в линейных единицах, таких как метры, сантиметры, дюймы и т. д.

Следует отметить, что длина, ширина, высота и глубина — это слова, которые являются производными от слов длинный, широкий, высокий и глубокий соответственно. Следовательно, они выражают размеры объекта. Обратите внимание на рисунок, приведенный ниже, чтобы увидеть длину, ширину и высоту прямоугольного параллелепипеда.

Длина против ширины

Разница между длиной и шириной фигуры заключается в том, что длина обозначает более длинную сторону, а ширина обозначает более короткую сторону фигуры.

Длина показывает длину фигуры, а ширина показывает, насколько она широка или широка. Ширину также называют широтой. Например, если две стороны прямоугольника равны 8 см и 3 см, мы можем легко определить, что длина прямоугольника равна 8 см, а ширина прямоугольника равна 3 см. Обратите внимание на прямоугольник, приведенный ниже, чтобы увидеть разницу между длиной и шириной фигуры.

Длина x Ширина x Высота

Длина, ширина и высота обычно используются вместе, чтобы найти объем геометрической фигуры, такой как прямоугольная призма, также известная как параллелепипед. Когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем. Это означает, что длина x ширина x высота = объем прямоугольного параллелепипеда. Другими словами, вместимость или объем кубоида или любой прямоугольной коробки можно измерить, если мы умножим эти три измерения вместе. Давайте разберемся в этом на примере.

Пример: Найдите объем прямоугольного параллелепипеда, если его длина 8 единиц, ширина 4 единицы, а высота 3 единицы.

Решение: Объем прямоугольного параллелепипеда можно рассчитать по формуле

Объем параллелепипеда = длина x ширина x высота

³

Длина Ширина Высота коробки

Длину, ширину и высоту коробки легко определить, потому что мы знаем, что длина — это самая длинная сторона, ширина — это более короткая сторона, а высота — вертикальный размер коробки. Обратите внимание на приведенный ниже рисунок, на котором показаны длина, ширина и высота ящика.

Эти размеры всегда выражаются в том порядке, в котором сначала идет длина, затем ширина и затем высота. Это означает, что если размеры коробки должны быть измерены, они выражаются в порядке длины, ширины и высоты. Например, 15 дюймов × 10 дюймов × 3 дюйма означает, что 15 дюймов — это длина коробки, 10 дюймов — ширина коробки и 3 дюйма — высота коробки.

☛Статьи по теме

• Измерение
• Преобразование длины
• Измерение длины

 

1. Пример 1: Найдите объем прямоугольного параллелепипеда, используя заданные длину, ширину и высоту: длина = 9 единиц, ширина = 5 единиц, высота = 4 единицы

   Решение: Формула, используемая для нахождения объема кубоида,

   Объем кубоида = Длина x Ширина x Высота

   После подстановки данных получаем, Объем кубоида = 9 × 5 × 4 = 180 единиц ³

   Следовательно, объем прямоугольного параллелепипеда равен 180 единицам ³

2. Пример 2: Найдите длину прямоугольного параллелепипеда, если его объем 196 кубических единиц, ширина 4 единицы, а высота 7 единиц.

   Решение:

   Формула, которая используется для определения объема прямоугольного параллелепипеда: , высота = 7, длина = ?

   После подстановки данных получаем 196 = длина × 4 × 7 ^.

   После решения этого уравнения мы получаем длину как, длина = 196/28 = 7 единиц.

   Следовательно, длина прямоугольного параллелепипеда равна 7 единицам.

3. Пример 3: Укажите истинное или ложное значение.

   а.) Длина показывает ширину фигуры.

   b.) Ширина также называется широтой.

   в.) Когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем.

   Решение:

   а) Неверно, длина показывает, насколько длинна фигура.

   б.) Правда, ширину называют еще широтой.

   в.) Правда, когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по длине ширине высоте

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о длине, ширине, высоте

Что такое Длина Ширина Высота?

Длина, ширина, высота, и глубина — это слова, образованные от прилагательных длинный, широкий, высокий и глубокий соответственно. Следовательно, они выражают размеры объекта. В то время как длина показывает длину данного объекта, ширина показывает, насколько он широк, а высота показывает, насколько он высок. Все они выражаются в линейных единицах, таких как сантиметры, метры, дюймы и так далее.

Какая формула для длины, ширины и высоты?

Когда длина, ширина и высота прямоугольного параллелепипеда перемножаются, получается объем прямоугольного параллелепипеда. Формула объема прямоугольного параллелепипеда: объем прямоугольного параллелепипеда = длина × ширина × высота.

В чем разница между длиной, шириной, высотой?

Длина, ширина, высота объекта — это различные размеры, выраженные в линейных единицах. В то время как длина — это самая длинная сторона фигуры, ширина — это более короткая сторона, а высота — это вертикальный размер или глубина фигуры.

Каков порядок длины, ширины, высоты?

Когда записываются размеры геометрической фигуры, они записываются в том порядке, в котором сначала идет длина, затем ширина и затем высота. Например, если необходимо выразить размеры прямоугольного параллелепипеда, его запишут как длина × ширина × высота, то есть 7 × 4 × 3, где 7 представляет длину, 4 — ширину, а 3 — высоту. кубоид.

Как рассчитать кубический метр по длине, ширине и высоте?

Кубический метр — это единица измерения объема прямоугольного параллелепипеда. Поэтому, чтобы найти объем прямоугольного параллелепипеда в кубических метрах, нужно перемножить длину, ширину и высоту. Следует отметить, что все длины, ширины и высоты должны иметь одни и те же единицы измерения (метры), чтобы объем выражался в кубических метрах. Например, если длина прямоугольного параллелепипеда 10 м, ширина 6 м, а высота 3 м, найдем его объем в кубических метрах. Объем кубоида = длина × ширина × высота. После подстановки значений получаем, Объем прямоугольного параллелепипеда = 10 × 6 × 3 = 180 кубических метров.

Какова длина, ширина и высота прямоугольного параллелепипеда?

Длина прямоугольного параллелепипеда равна наибольшей стороне, когда параллелепипед расположен горизонтально. Ширина — это более короткая сторона прямоугольного параллелепипеда. Высота — это вертикальный размер прямоугольного параллелепипеда.

Как найти длину, ширину и высоту, если задан объем?

Формула, которая используется для нахождения объема прямоугольного параллелепипеда: Объем прямоугольного параллелепипеда = длина × ширина × высота. Следовательно, если какое-либо одно измерение отсутствует, его можно рассчитать с помощью этой формулы, заменив другие заданные значения. Например, найдем высоту прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 144 кубических см, длина = 12 см, ширина = 2 см.