В форме уравнения кинетическая энергия твердого тела представлена ​​как половина массы тела, умноженная на квадрат его скорости, плюс половина момента инерции массы, умноженная на квадрат угловой скорости. Если мы хотим определить изменение кинетической энергии, мы просто возьмем конечную кинетическую энергию минус начальную кинетическую энергию. 92 \right) \]

Потенциальная энергия, в отличие от кинетической энергии, на самом деле вовсе не энергия. Вместо этого он представляет собой работу, которую данная сила потенциально может совершить между двумя моментами времени. Потенциальная энергия может проявляться во многих формах, но две из них, которые мы обсудим здесь, — это гравитационная потенциальная энергия и упругая потенциальная энергия. Они представляют собой работу, которую совершат сила тяжести и сила пружины соответственно. Мы часто используем эти термины потенциальной энергии вместо работы силы тяжести или пружин соответственно. При включении этих терминов потенциальной энергии важно также не включать работу силы тяжести или силы пружины.

Изменение гравитационной потенциальной энергии для любой системы представлено массой тела, умноженной на значение \(г\) (9,81 м/с ² или 32,2 фута/с ² на поверхности земли), умноженное на изменение высоты по вертикали между начальным положением и конечным положением. В форме уравнения это выглядит следующим образом. \[ \Delta PE = m * g * \Delta h \]

В отличие от работы и кинетической энергии, вращательной версии гравитационной потенциальной энергии не существует, так что это в точности то же самое, что мы имели для частиц.

Чтобы определить изменение упругой потенциальной энергии, нам придется идентифицировать любые линейные пружины (как мы это делали для частиц), а также любые пружины кручения и пружинные константы для каждой из этих пружин.

Чтобы найти изменение упругой потенциальной энергии, нам нужно знать жесткость любой пружины в задаче (представленной \(k\), в единицах силы на расстояние для линейных пружин или момента на угол закручивания для торсионных пружин ), а также расстояние или угол, на который пружина была растянута выше или ниже ее естественного положения покоя. Это отличие от положения покоя представлено расстоянием \(x\) для линейных пружин или углом \(\theta\) для торсионных пружин. Как только мы получим эти значения, упругую потенциальную энергию можно рассчитать, умножив половину жесткости на квадрат расстояния \(x\) или угол \(\theta\) в квадрате. Чтобы найти изменение упругой потенциальной энергии, мы просто берем конечную упругую потенциальную энергию минус начальную упругую потенциальную энергию. 92 \]

Возвращаясь к нашему первоначальному уравнению сохранения энергии, мы просто подставляем соответствующие члены с каждой стороны (работа слева и энергии справа) и уравновешиваем две части, чтобы найти любые неизвестные. Члены, которые не существуют или не меняются (например, упругая потенциальная энергия в задаче без пружин или \(\Delta KE\) в задаче, в которой скорость тела не изменяется) могут быть установлены равными нулю. . Опять же, есть только одно уравнение, поэтому мы можем решить только для одного неизвестного, если мы не дополним уравнение сохранения энергии другими уравнениями отношений.

Пример \(\PageIndex{1}\)

Проигрыватель проигрывателя пластинок состоит из диска диаметром 12 дюймов и весом 5 фунтов. Двигатель разгоняет поворотный стол из состояния покоя до рабочей скорости 33,33 об/мин за один оборот. Какую работу совершает двигатель? Какой средний крутящий момент развивает двигатель?

Решение

Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Маджидом Чацазом. Источник YouTube: https://youtu.be/UPHgU-o80Q0.

Пример \(\PageIndex{2}\)

Показанная ниже система используется для пассивного замедления опускания ворот. Ворота можно представить как плоскую пластину по краю массой 25 кг и высотой 2 метра. Предположим, что пружина не растянута, как показано на диаграмме.

• Какой была бы угловая скорость ворот без пружины?
• Если мы хотим уменьшить угловую скорость на дне до 25% от ее первоначального значения, какой должна быть жесткость пружины?

Решение

Видео \(\PageIndex{3}\): Рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Маджидом Чацазом. Источник YouTube: https://youtu.be/HCAC0tNR18w.

Пример \(\PageIndex{3}\)

Сферический шар массой 5 ​​кг и радиусом 0,05 метра помещается на пандус, как показано ниже. Если мяч катится без проскальзывания, какова скорость мяча в нижней части пандуса?

Решение

Видео \(\PageIndex{4}\): Рабочее решение примера проблемы \(\PageIndex{3}\), предоставленное доктором Маджидом Чацазом. Источник YouTube: https://youtu.be/p2pvQ0kCWIU.

Пример \(\PageIndex{4}\)

16-килограммовый полуцилиндр помещают на твердую плоскую поверхность, как показано ниже, и отпускают из состояния покоя. Какова будет максимальная угловая скорость при раскачивании взад-вперед?

Решение

Видео \(\PageIndex{5}\): Рабочее решение примера проблемы \(\PageIndex{4}\), предоставленное доктором Маджидом Чацазом. Источник на YouTube: https://youtu.be/HpRtDQjoEBA.

Пример \(\PageIndex{5}\)

Механизм состоит из двух трехкилограммовых колес, соединенных с двухкилограммовым стержнем, как показано ниже. Основываясь на размерах на диаграмме, какова минимальная необходимая начальная скорость для колес, чтобы гарантировать, что механизм сделает полный оборот за один оборот без раскачивания назад?

Раствор

Видео \(\PageIndex{6}\): Рабочее решение примера проблемы \(\PageIndex{5}\), предоставленное доктором Маджидом Чацазом. Источник YouTube: https://youtu.be/8cjQ1S6yOTc.

Эта страница под названием 13.1: Сохранение энергии для твердых тел распространяется в соответствии с лицензией CC BY-SA 4. 0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джейкоб Мур и авторы

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. энергетический метод
   2. источник@http://mechanicsmap. psu.edu

Внутренняя энергия: определение, формула и изменение

Сегодня суббота, и у вас есть билеты, чтобы пойти на футбольный стадион, чтобы посмотреть матч вашей любимой команды (вы можете заменить футбол на любой вид спорта, не волнуйтесь). Но вы читали много статей на StudySmarter и теперь работаете физиком на полную ставку. Итак, как только вы садитесь со своим напитком и закусками, вы смотрите на своего любимого игрока и представляете его просто как частицу. И когда вы отводите взгляд, все футбольное поле уже не поле, а пространство, заполненное физическими частицами. Конечно, вы хотите получить удовольствие от матча, но сначала у вас возникает вопрос, и вам нужно на него ответить. Обладает ли система реальных частиц полной кинетической энергией, как и игроки на поле?

Помните, что система в физике — это любая часть Вселенной, которую мы хотим изучить.

Ответ на этот вопрос – да. Точно так же, как игроки на футбольном поле, частицы в системе движутся. Частицы внутри этой системы обладают определенной кинетической энергией из-за температуры системы: частицы обычно движутся быстрее, когда температура системы выше. Кроме того, частицы могут иметь и потенциальную энергию, например, за счет взаимного притяжения между частицами (например, если они являются электрическими диполями).

Определение внутренней энергии

Внутренняя энергия системы – это энергия, содержащаяся внутри. Это сумма всех микроскопических кинетических и потенциальных энергий частиц в системе, если бы система находилась в состоянии покоя, а не в макроскопическом энергетическом потенциале.

Важно понимать, что эта внутренняя энергия не имеет прямого отношения к внешней энергии системы. Это означает, что если система движется и обладает кинетической энергией, то внутренняя энергия системы не включает эту энергию, возникающую в результате общего движения системы. Точно так же, если мы поместим всю систему на высоте над землей, эта макроскопическая потенциальная энергия не повлияет на внутреннюю энергию системы. Система может быть совершенно неподвижной и не иметь кажущейся энергии, пока ее внутренняя энергия изменяется, но, с другой стороны, система может двигаться, в то время как ее внутренняя энергия постоянна.

Если мы нагреем воду, макроскопическая энергия системы не увеличится, поскольку вода не движется. Однако мы знаем, что что-то происходит, потому что температура воды повышается. По мере повышения температуры воды частицы воды начинают двигаться все быстрее и быстрее, что приводит к увеличению их общей кинетической энергии. Таким образом, внутренняя энергия воды увеличивается по мере нагревания воды. При этом внешняя кинетическая энергия остается равной нулю.

В общем случае изменение внутренней энергии системы вызывает либо изменение температуры, либо изменение состояния.

Внутренняя энергия — экстенсивное свойство: свойство системы, которое зависит от того, как система оценивает свой размер или массу. Его значение можно описать как сумму значений более мелких подразделений системы.

Для реальных систем нас обычно интересует (и, следовательно, вычисляется) изменение внутренней энергии во время процесса, такого как повышение температуры.

Внутренняя энергия в термодинамике

В физике энергия передается в результате изменения температуры, приложения сил и т. д. Разделом, изучающим это, является термодинамика .

Термодинамика — это раздел физики, изучающий взаимосвязь между теплом, работой и другими видами передачи энергии.

Теперь представьте себе любую систему (и на этот раз это не обязательно должен быть футбольный стадион). Помните, что система в термодинамике — это любая часть Вселенной, которую мы хотим изучить, то есть это может быть человеческое тело, определенное количество жидкости, растение или что-то еще, что вы можете себе представить.

Термодинамическая система с границей, адаптированная из изображения Krauss CC BY-SA 4. 0

Частицы с микроскопическими энергиями находятся внутри системы, и сумма всех этих микроскопических энергий составляет то, что мы называем внутренней энергией.

Это приводит нас к изучению того, что происходит с внутренней энергией, когда часть энергии передается системе. В нашем случае мы сосредоточимся на том, что происходит, когда температура увеличивается. Для этого в систему должна быть передана энергия , , поэтому либо система должна быть нагрета, либо в системе должна быть выполнена работа.

Тепло — это энергия, передаваемая в систему или из системы за счет разницы температур с окружающей средой.

Тепло, добавленное к системе или отведенное от нее, не следует путать с температурой системы.

Теплопередача вызывает изменение внутренней энергии системы. Точно так же приложение работы к системе увеличивает внутреннюю энергию системы.

Теплообмен между двумя системами при разных температурах, адаптировано из изображения BlyumJ CC BY-SA 4. 0

Изменение внутренней энергии системы может изменить либо потенциальную энергию частиц, либо кинетическую энергию частиц. Если потенциальная энергия изменяется, мы говорим об изменении состояния. Если кинетическая энергия изменяется, мы говорим об изменении температуры.

Температура системы является мерой полной кинетической энергии в системе. Когда тепло поступает в систему и не происходит изменения состояния, внутренняя энергия увеличивается, а, следовательно, увеличивается и общая кинетическая энергия. Это означает, что температура повышается.

Изменения внутренней энергии

Как указывалось ранее, изменение внутренней энергии системы вызывает либо изменение температуры, либо изменение состояния. Мы рассмотрим изменения температуры в следующем разделе, а здесь сосредоточимся на изменениях состояния.

Как вы знаете, мы обычно различаем три состояния вещества: газ, жидкость и твердое тело . Если температура системы повышается или понижается до определенной точки, которая зависит от вещества, с которым мы работаем, может произойти переход из одного состояния в другое. При этом изменении состояния температура остается постоянной, но внутренняя энергия системы все же изменяется.

Во-первых, внутренняя энергия системы может увеличиться, в результате приложения некоторого количества тепла или работы. Это три различных изменения состояния, связанные с увеличением внутренней энергии:

• Твердое тело будет плавиться , образуя жидкость.
• Жидкость будет испаряться, превращаясь в газ.
• Если у нас есть твердое тело и оно сразу превращается в газ при увеличении внутренней энергии, мы говорим о сублимации .

В противном случае мы можем уменьшить внутреннюю энергию вещества, когда система начинает отдавать теплоту наружу или совершает работу в окружающей среде:

• Газ будет конденсироваться, получать жидкость.
• Жидкость замерзнет, ​​ превратится в твердое тело.
• Если вещество переходит из газообразного состояния в твердое, минуя свое жидкое состояние, говорят об отложении .

Повышая и понижая температуру, мы можем изменить состояние материи, адаптировано из изображения Enos CC BY-SA 4.0

Вы можете узнать больше об изменениях состояния здесь, в StudySmarter.

Уравнение изменения внутренней энергии

В большинстве случаев изменение внутренней энергии вызывает изменение температуры. При этом меняется только полная кинетическая энергия частиц, а полная потенциальная энергия остается неизменной.

тепловая энергия системы представляет собой сумму всех микроскопических кинетических энергий частиц в системе, если бы система находилась в состоянии покоя.

Короче говоря, тепловую энергию можно рассматривать как кинетическую часть внутренней энергии. Когда во время процесса не происходит изменения состояния, изменение внутренней энергии совпадает с изменением тепловой энергии системы.

Уравнение, связывающее изменение тепловой энергии и изменение температуры системы, имеет вид

.

В символах это уравнение принимает вид

,

, где

• — изменение тепловой энергии системы. Стандартной единицей является джоуля.
• — масса системы. Стандартной единицей является килограмма .
• называется удельной теплоемкостью . Определяется как количество энергии, необходимое для повышения температуры единицы массы определенного вещества на одну единицу температуры. Каждое вещество имеет свою постоянную удельную теплоемкость: это такая же характеристика, как плотность и цвет. Стандартная единица измерения j oule/(килограмм x кельвин) ,. Это всегда положительно.
• — изменение температуры системы. Если конечная температура меньше начальной температуры, значение будет отрицательным. Стандартной единицей измерения является кельвина , .

Как видите, если масса вещества не меняется в процессе (поэтому имеет постоянную величину), то температура системы увеличилась бы, если бы мы увеличили ее тепловую энергию. При определенном энерговкладе изменение температуры зависит от массы системы и удельной теплоемкости материала, из которого состоит система. Для двух систем с двумя разными веществами с одинаковой массой, одинаково изменяющими тепловую энергию обеих систем, изменение температуры будет различным. Это связано с тем, что два вещества будут иметь разные значения удельной теплоемкости.

Внутренняя энергия системы также может быть изменена с помощью работы .

В термодинамике обычно говорят о расширении и сжатии. Когда объем системы увеличивается, мы говорим о расширении, а когда он уменьшается, мы говорим о сжатии.

Примеры а) расширения и б) сжатия системы, адаптированные из образа MikeRun CC BY-SA 4.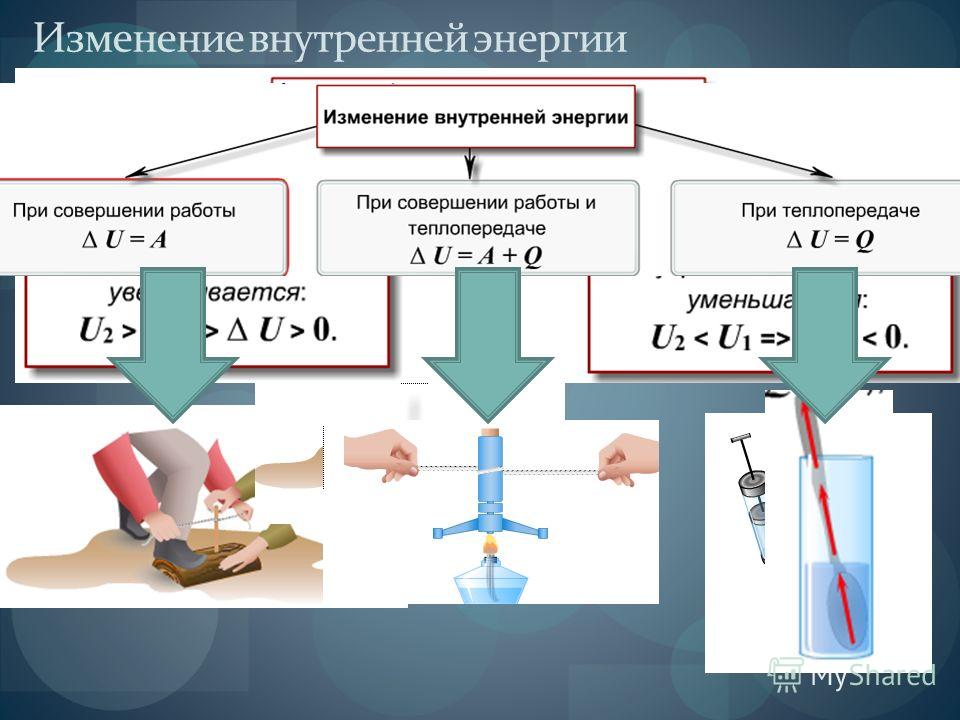 0

Работа над системой приведет к ее сжатию. Какая работа необходима для сжатия системы на определенный объем, определяется давлением в системе по следующей формуле:

,

, где

• — работа, выполненная в системе.
• — давление в системе. Стандартной единицей давления является паскаля.
• разница в объеме системы, вызванная выполняемой работой. Эта разница отрицательна, если система сжата. Стандартной единицей является кубических метра .

Если мы работаем над системой, то из формулы мы видим, что разница в объеме отрицательна, значит, у нас действительно есть сжатие. Точно так же, если система работает в своей среде, она будет расширяться.

Примеры внутренней энергии

Теперь, когда мы поняли, что такое тепловая энергия и внутренняя энергия, давайте проведем некоторые расчеты, связывающие изменения тепловой энергии с изменениями температуры. Если нет изменений состояния, изменение тепловой энергии равно изменению внутренней энергии.

Вопрос

Представьте, что у вас есть масса воды. Если температуру этой массы воды увеличить от до, какое количество тепловой энергии прибавилось к воде? Удельная теплоемкость воды.

Решение

Нам просто нужно применить уравнение изменения тепловой энергии:

.

Заметим, что разница температур есть. Если мы подставим данные значения в уравнение, то получим следующий результат:

.

Мы заключаем, что тепловая энергия была добавлена ​​к воде для того, чтобы ее температура была повышена, как указано в вопросе. Мы не знаем, как эта энергия была добавлена! Это могло быть теплопередачей или работой.

Вопрос

Представьте, что у нас есть вещество, и мы хотим выяснить, что это за материал. Мы решили, что можем измерить его удельную теплоемкость, а затем посмотреть, какой материал обладает этой удельной теплоемкостью. Нагреваем материал, увеличивая внутреннюю энергию на . Мы не видим изменения состояния и измеряем изменение температуры. Какова удельная теплоемкость этого материала? Какой материал у нас есть?

Раствор

Не было никакого изменения состояния, поэтому изменение внутренней энергии является изменением тепловой энергии. Снова нам нужно использовать уравнение изменения тепловой энергии, но на этот раз нам нужно выделить удельную теплоемкость следующим образом:

.

Теперь мы можем подставить значения в уравнение:

.

Удельная теплоемкость. Если мы посмотрим на таблицу удельной теплоемкости, то обнаружим, что у железа есть эта удельная теплоемкость, поэтому, скорее всего, у нас есть железо.

Внутренняя энергия — основные выводы

• Термодинамика — это раздел физики, изучающий взаимосвязь между теплотой, работой и другими видами передачи энергии.
• Термодинамическая система является ограниченной частью Вселенной.