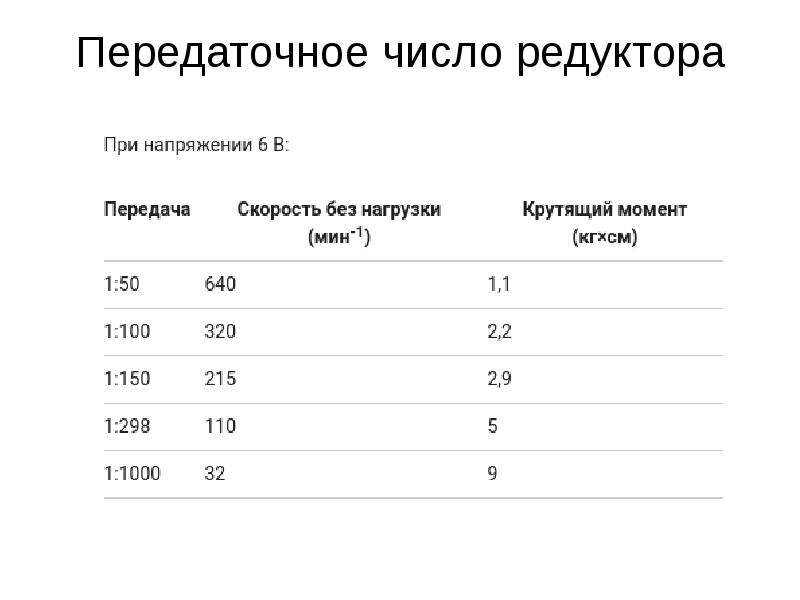
Передаточное число редуктора

Передаточное отношение — это соотношение угловых скоростей или крутящих моментов валов (в зависимости от строения механизма).
Передачи применяются для того, чтобы передать вращающий момент от электродвигателя к исполнительному устройству. Почему это необходимо? Дело в том, что сам мотор обычно не может передать требуемый вращающий момент, кроме того, частота вращения вала электродвигателя оказывается слишком велика, поэтому её надо понизить. Для этого и сконструированы понижающие передачи, редукторы. Таким образом удаётся изменить сразу и частоту вращения вала, и крутящий момент.

Передачи с крутящим моментом

Механизм передачи крутящего момента — редуктор — имеет входной и выходной валы.
Существует два способа передачи вращающего момента: жёсткий (момент передается жесткими звеньями, например, шестернями) и фрикционный (момент передается силами трения, работающих на поверхностях вала, например, ременная передача). Также есть возможность совмещать эти способы передачи.
Характеристика зубчатой передачи редуктора
Зубчатая передача редуктора – это механизм, состоящих из отдельных звеньев для передачи мощности через вращение зубчатых колёс. Такую зубчатую передачу используют в механических редукторах для преобразования движения.
Зубчатые редукторы очень часто задействуют в машиностроении. Именно их выбирают благодаря большому количеству преимуществ: высокому КПД, долгому сроку службы механизма, маленьким габаритам, постоянству передаточного отношения, простой и надёжной конструкции.
Также у этих редукторов есть и недостатки. К ним относят шум при больших скоростях и большие размеры редукторов, если передаточные отношения велики. Тем не менее, плюсов их использования гораздо больше, чем минусов, что и определяет итоговую востребованность.

Многоступенчатые редукторы

Как известно, современные электродвигатели выдают частоту ведущего вала примерно в районе полутора тысячи (1500) оборотов в минуту. А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству?
Здесь на помощь как раз и придут многоступенчатые редукторы. Наличие нескольких ступеней позволяет сделать компактное устройство, значительно снижающее частоту вращения вала.

Как правильно рассчитать передаточное число

Передаточное число многоступенчатого редуктора вычисляется как произведение передаточных чисел каждой ступени. Пример. В редукторе четыре зубчатые пары, передаточные отношения каждой из которых тоже равны 4. Общее передаточное число тогда будет равно 4х4х4х4 = 256.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается. Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.

Расчёт без учета сопротивления

Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.

Важно! При этом надо смотреть, меняется ли направление вращения шестеренки. Если меняется, то передаточное отношение принимается со знаком минус, если не меняется, то плюс. Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.

Если в передаче участвует так называемая паразитка, то она в расчете передаточного отношения не участвует, так как ее задача лишь менять направление движения.
Также при расчете передаточных отношений можно использовать наружный диаметр шестерни. Иногда это удобно, если посчитать число зубьев затруднительно. Важно: зубчатая передача жесткая, здесь нет проскальзывания, как в ременной передаче, поэтому передаточное число всегда можно рассчитать с абсолютной точностью.
Если в редукторе применен червячный редуктор, то его передаточное отношение определяется как отношение числа зубьев ведущего колеса к числу заходов (витков) червяка. Чаще всего у червяка один заход, поэтому ясно: передаточное отношение червячной пары огромно, а вращающий момент может повышаться в десятки раз.

КПД зубчатой передачи

Преимуществами данной передачи считаются:

1. Большая и неограниченная мощность.
2. Небольшая масса и габариты.
3. Большой коэффициент полезного действия (приблизительно 0,95-0,99).
4. Надёжны, но нуждаются в большой точности изготовления.

КПД определяется как отношение реально полученной энергии к потребленной. Чем выше КПД механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Учёные всего мира постоянно ведут борьбу именно за сокращение непроизводительных потерь. Чтобы обеспечить хорошую работу машины с большим КПД, можно использовать масла с различными свойствами при больших изменениях температуры среды. При экспериментах с различными видами масла совместно с допустимой нагрузочной способности зубчатых передач на рабочих поверхностях зубьев не обнаружили развитие процесса разрушения, что обеспечивает отличные технико-экономические показатели машины.

Важно! КПД зубчатой передачи сильно зависит от точности изготовления зубчатых колес. В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей.

Постоянное и переменное передаточное отношение редуктора

Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом — их полезность уже проверена временем.

8.4: Передаточное отношение

Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза.

В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.

Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.

Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.

Пример 8.1

В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.

Длина на выходе / Длина на входе = 8 / 2 = 4

Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду.

В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.

Пример 8.2

В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?

Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:

Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м

Далее, необходимо рассчитать равнодействующую силу на выходе:

Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон

Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!

Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.

Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.

Пример 8.3

Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.

Пример 8.4

В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).

Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.

Из примеров 8.1 — 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.

Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.

Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67

 

Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5

Глядя на пример, представленный выше…

Предельный перегрузочный момент второго вала может быть рассчитан по формуле:

Выходной момент = Входной момент х Передаточное число

Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м

Свободная скорость второго вала может быть рассчитана по формуле:

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин

Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.

Для второго примера расчеты могут быть произведены тем же способом.

Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2

Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин

Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.

 

Простое объяснение передаточного числа | Наука

Обновлено 25 апреля 2017 г.

Автор Grahame Turner

То, как шестерни взаимодействуют друг с другом, важно знать всем, кто планирует максимально использовать их. У большинства современных автомобилей передаточные числа рассчитываются с помощью компьютеров, но у велосипедов и механических домашних проектов их нет.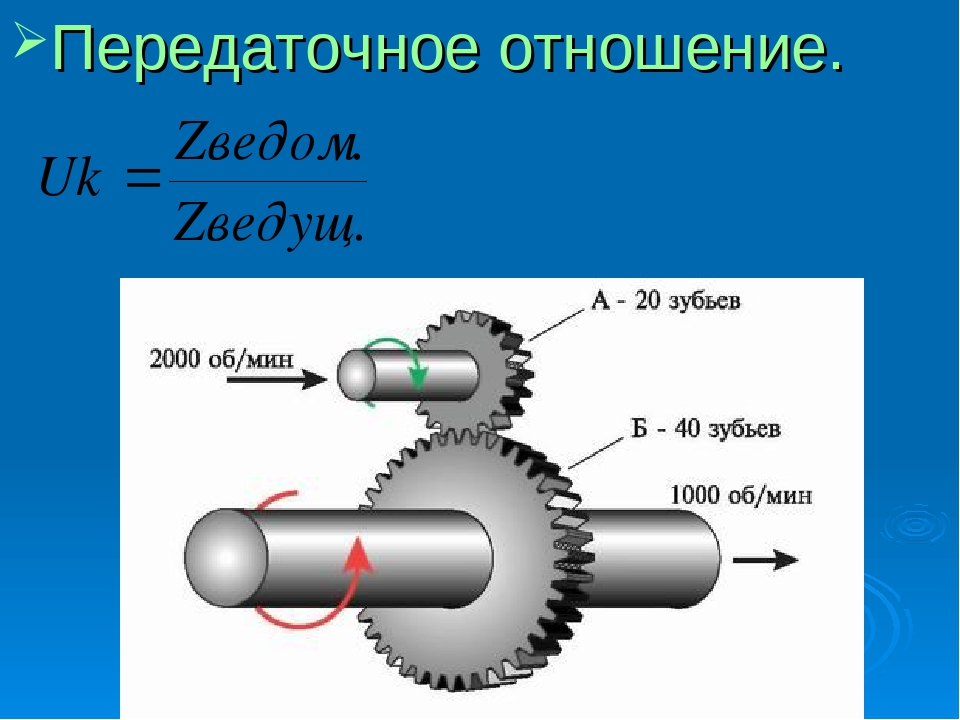 Если вас озадачивают передаточные числа, вам будет полезно узнать, что такое передаточное число и как оно влияет на другие части вашего механического устройства.

Передаточное отношение

Если несколько шестерен входят в зацепление, количество зубьев на них образует важное передаточное число: передаточное число. Когда несколько шестерен входят в зацепление, они образуют так называемую зубчатую цепь. Передаточное отношение рассчитывается только для первой передачи, ведущей шестерни, которая подключена к источнику питания, и последней передачи в цепи. Если вы подсчитаете количество зубьев на первой шестерне и на шестерне X (последней) и установите их в соотношении (1: X), это и будет передаточное число. Если число можно уменьшить, то следует его уменьшить, например, соотношение 100 зубов:40 зубов сокращается до 5:2.

Скорость и передаточное число

Передаточное отношение необходимо для расчета скорости, которую будет производить данная зубчатая цепь. Когда у вас есть эта информация, у вас есть половина информации, необходимой для расчета скорости. Уравнение: Скорость (Шестерня 1) * Зубья (Шестерня 1) = Скорость (Шестерня X) * Зубья (Шестерня X). Таким образом, если у вас есть скорость, с которой двигатель передает шестерни, вы можете очень легко рассчитать скорость шестерни X.

Шкивы

••• шестерни и складной инструмент изображение Раду Развана из Fotolia.com

На велосипеде используется немного другая система: вместо пары шестерен, сцепленных напрямую, они соединены цепью шкивов, но передаточное число сохраняется. Например, на горном велосипеде к педалям прикреплены концентрические шестерни, а к ведущему колесу — еще несколько шестерен. Отношение зубьев колесной шестерни к зубьям педальной шестерни по-прежнему будет формировать соотношение — и если вы крутите педали с заданной скоростью на велосипеде, изменение этого передаточного числа изменит скорость, с которой вы едете.

Промежуточные шестерни

••• механические шестерни и шестерни image by patrimonio designs from Fotolia. com

В зубчатой ​​цепи, когда несколько шестерен находятся в середине, со средними шестернями происходит нечто довольно интересное. Возможно, вы заметили, что в предыдущих расчетах важны только первая и последняя передачи. Это потому, что промежуточные передачи не влияют на скорость — они будут двигаться так быстро или медленно, как им нужно. Однако они изменят направление: если число передач нечетное, первая и последняя будут вращаться в одном направлении.

Преимущества

Преимущество знания передаточного числа заключается в том, что вы можете использовать его для получения механических преимуществ. Существует компромисс между скоростью и крутящим моментом, то есть мощностью вращения. Когда передаточное число 1:1, величина крутящего момента одинакова, и скорость одинакова. Однако, как только вы увеличите передаточное число (например, 1:4), вы уменьшите крутящий момент, но значительно увеличите скорость. Если вы измените соотношение (скажем, 4:1), вы уменьшите скорость, но увеличите крутящий момент.

Передаточное отношение — VEX ROBOTICS COMPETITION

A Передаточное число Изменение — это один из самых простых способов изменить механическое преимущество в механизме или системе для достижения желаемой скорости и/или крутящего момента. Использование шестерен разного размера, сцепленных вместе в зубчатой ​​передаче, может изменить скорость или крутящий момент, обеспечиваемый двигателем.

Зависимости скорости/крутящего момента обратны друг другу, т. е. противоположны. Когда вы увеличиваете скорость, вы уменьшаете крутящий момент. Когда вы увеличиваете крутящий момент, вы уменьшаете скорость. Крутящий момент можно рассматривать как мощность, обеспечиваемую крутящим моментом на приводном валу.

Передаточное отношение можно рассчитать математически, подсчитав количество зубьев на шестерне. Вот веб-сайт WikiHow

, который поможет вам в этом.

Когда большая шестерня соединена с двигателем, а меньшая шестерня приводится в действие, скорость увеличивается. Это работает, потому что меньшая шестерня вращается быстрее, чем большая шестерня, поскольку у нее меньше зубьев. Когда вы увеличиваете скорость, используя этот тип передаточного числа, вы жертвуете крутящим моментом. Когда две шестерни сцеплены вместе, они вращаются в противоположных направлениях.

Когда меньшая шестерня подключена к двигателю и приводится в действие большая шестерня, скорость уменьшается. Это работает, потому что большая шестерня вращается медленнее, чем меньшая, поскольку у нее больше зубьев. Много раз вам потребуется замедлить механизмы, чтобы увеличить крутящий момент в системе передач. Когда две шестерни сцеплены вместе, они вращаются в противоположных направлениях.

Когда две шестерни одинакового размера входят в зацепление, скорость или крутящий момент не изменяются. Ведомая шестерня имеет тот же крутящий момент или скорость, что и ведущая шестерня двигателя. Одной из причин, по которой вы можете захотеть это сделать, является передача движения шестерни в другую часть робота.

Иногда между двумя шестернями используется шестерня. Эта шестерня называется промежуточной шестерней. Причина, по которой вы хотели бы добавить промежуточную шестерню, состоит в том, чтобы изменить направление ведомой шестерни. Когда между двумя шестернями используется одна промежуточная шестерня, ведущая и ведомая шестерни вращаются в одном направлении. Не имеет значения размер промежуточной шестерни, важны только размеры ведущей и ведомой шестерен при рассмотрении передаточных чисел для скорости и крутящего момента.

Иногда для передачи движения другой части робота используется несколько промежуточных шестерен.