Пружины подвески и их цветовая маркировка
Один из часто задаваемых вопросов менеджерам интернет магазина: «какие пружины лучше поставить», «что значит желтая метка?». В эти вопросы постараюсь внести небольшую ясность и может быть поле для размышлений.
Для начала разберемся что из себя представляет пружина подвески, на первый взгляд на что может влиять такой простой элемент как пружина. Многие люди вовсе не обращают внимание на износ данного элемента, но это не удивительно ведь она не требует какой-либо настройки никаких рем. комплектов и спец. ухода. Но мало кто понимает, что пружины не все одинаковые и различие их не только в жесткости. Пружин подвески существует 5 видов, но так далеко в строение пружин и их возможности мы заходить не будем, рассмотрим самые распространенные варианты пружин, стандартные, те что устанавливаются на автомобили ВАЗ, ЗАЗ, ГАЗ, АЗЛК.
На некоторые модели ВАЗ устанавливаются пружины так называемые «бочкообразные», для увеличения сопротивления качению.
Также устанавливались, но намного реже, пружины с переменным шагом витка которые обеспечивали оптимальную устойчивость с малыми нагрузками, таких как боковой крен, резкое торможение, ускорение. И пропорционально увеличивалась жесткость, что исключало пробои подвески и сохраняло комфорт движения по неровностям.
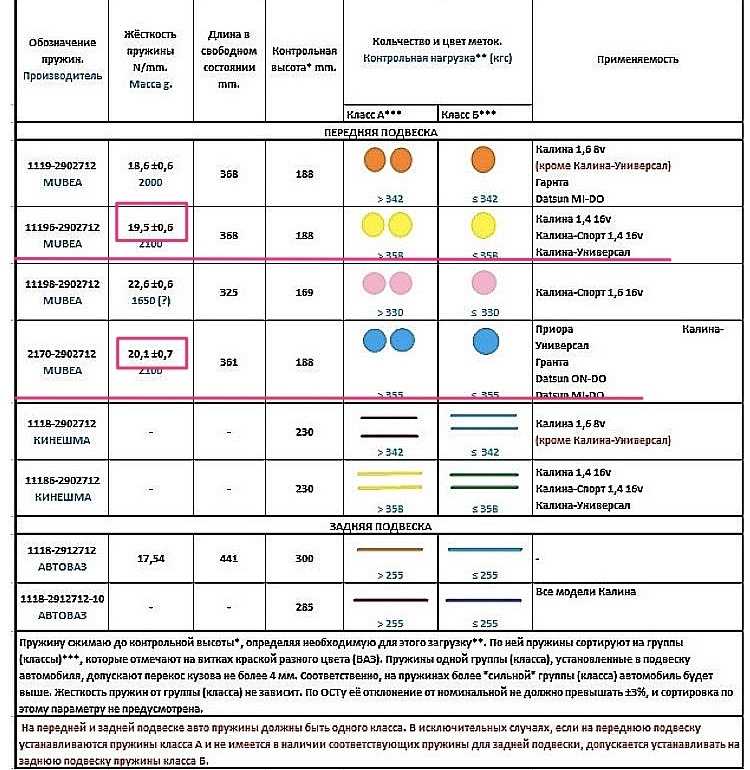
Стандартные пружины которые устанавливались на автомобили ВАЗ, ЗАЗ, ГАЗ, АЗЛК является оптимальным вариантом для установки, подробно рассмотрим именно их. Изготовление пружин достаточно сложный процесс, по этапно его можно разделить на: нагрев и накручивание прута из прокатной пружинной стали, с которой шлифованием или токарной обработкой сняли обезуглероженный слой затем они проходят закалку в масле, следующий этап холодная осадка, затем наноситься защитный слой (при этом задние и передние пружины могут покрываться разными защитными смесями) ну и конечный этап это ОТК после которого и присваиваться класс жесткости (плюсовое поле допуска по нагрузке относиться к, классу «A» (обычно желтая метка), с минусовым – к «Б» (зеленая метка)).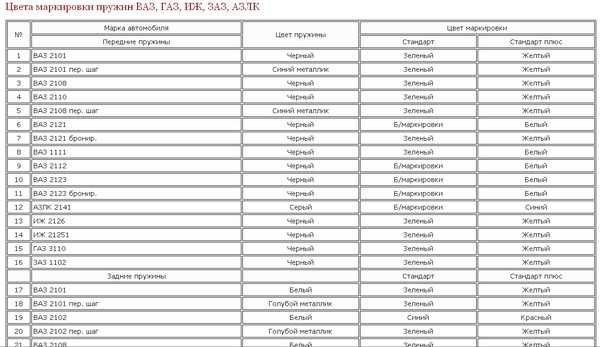
При этом на пружину наносить цветовое обозначение соответствующего класса. Стандартная цветовая маркировка ВАЗ, ЗАЗ, ГАЗ, АЗЛК для передних пружин на черной пружине зеленая или желтая метка, которые соотвецтвуют классу жесткости. На задних пружин используется ненамного иная маркировка: на белой пружине ставиться те же метки зеленая и желтая, но для пружин с увеличенной длиной таких как 2102, 2104 используется маркировка синим и коричневым(красным).
В полнее законный вопрос «а какие же пружины лучше?» в зависимости в каких условиях эксплуатируется автомобиль. Например если вы часто ездите с максимальной нагрузкой то лучше установить пружины класса «А», также для таких условий АвтоВАЗ выпускает пружины предназначены в основном для задней оси (2102, 2104, 2111), отличают которые от стандартных пружин другая длина, некоторые водители устанавливают увеличенные проставки пружины для того чтобы увеличить дорожный просвет, но стоит понимать что управляемости и комфорта она не добавит (уменьшает ход отбоя и увеличивает ход сжатия амортизатора).
Если пружина села, то проставками ее не спасти, потому что это уменьшит расстояние до межвиткового смыкания. Такая же бесполезная операция вставлять между витков резиновые прокладки, они так же не спасут положение. Самое главное при установки пружин поставить пружины одного класса на ось, допускается установка разных классов на оси например класс «Б» на заднюю ось, а на переднюю «А», но на оборот никак нельзя.
Пружины задней подвески АСОМИ Comfort PRO для ВАЗ 2110-12
Характеристики
Вес: 5.75 кг.
Цена: Нет в наличии
Наличие: Нет
Мы в соц. сетях:
Пружины подвесок воспринимают и передают вертикальные нагрузки от колес к кузову автомобиля, снижают динамический уровень нагрузок при движении автомобиля по неровностям дороги и обеспечивают необходимую плавность хода автомобиля.
Пружины ТМ АСОМИ имеют цилиндрическую конструкцию с переменным значением шага навивки рабочих витков. Посадочные параметры опорных витков соответствуют пружинам, применяемым в подвеске переднеприводных автомобилей ВАЗ.
В отличие от «серийных пружин», устанавливаемых в подвеску производителем автомобиля, пружины ТМ АСОМИ отличаются конструктивно, изменяя свою жесткость с увеличением полезной нагрузки – этим качественно меняются параметры подрессоривания автомобиля.
Обеспечивается это тем, что для частичных нагрузок задействованы все рабочие витки пружины, а при дальнейшем нагружении количество рабочих витков уменьшается (соприкасаясь с опорными). Кроме этого, для разгруженного состояния высота задних пружин уменьшена на 8 мм. В результате, при частичных нагрузках автомобиль имеет меньшую высоту и достаточно «мягкую» подвеску. При полной и близкой к ней нагрузкам имеет высоту, аналогичную серийным пружинам, но при этом более жесткую подвеску, обеспечивающую лучшую устойчивость и управляемость автомобиля и большую энергоемкость.
Это хорошо видно по характеристикам упругости пружин, представленным на рис. 1.
Ри. 1. График характеристик упругости серийных пружин и пружин ТМ АСОМИ.
При малых деформациях их жесткость близка к серийным пружинам. При деформации более 100 мм жесткость пружин прогрессивно возрастает и превышает начальную жесткость на 25…30%.
Исходным условием создания прогрессивных пружин ТМ АСОМИ было обеспечение технологией изготовления более высоких свойств материала после закалки и отпуска. В результате пружины ТМ АСОМИ изготовлены из качественного проката и подвергнуты специальной термомеханической обработке. Упрочнение материала, полученное в результате данной технологии, позволяет работать пружине при повышенных напряжениях. Изменение шага витков подобрано таким образом, что осадки не происходит даже при полном сжатии пружины. Пружины ТМ АСОМИ имеют специальное защитное покрытие на основе эпоксидного порошка, наиболее стойкое к ударам и повреждению, что обеспечивает длительный срок эксплуатации пружин.
Как и серийные, пружины ТМ АСОМИ делятся на классы А и Б по статической нагрузке. Маркировка производится полосой краски:
- желтая — класс А
- зеленая — класс Б
Порядок установки пружин ТМ АСОМИ аналогичен серийным пружинам.
Таким образом, пружины ТМ АСОМИ имеет следующие преимущества:
- улучшают устойчивость и управляемость автомобиля
- повышают энергоемкость подвески
- обеспечивают лучшую плавность хода при малых нагрузках, и повышают жесткость по мере увеличения полезной нагрузки, уменьшая изменение собственной частоты колебаний кузова
- улучшают аэродинамику автомобиля при частичной нагрузке
- обеспечивают высокую долговечность за счет специальной термомеханической обработки и высокопрочного порошкового покрытия.
Пружины подвески А110.2912.712-10 предназначены для применения в задней подвеске автомобилей семейства LADA 110, 111, 112 и их модификаций, LADA 21106, 21123, 21128, выпускаемых мелкими сериями, а также в подвеске автомобилей семейств LADA Priora, LADA Kalina, LADA Granta.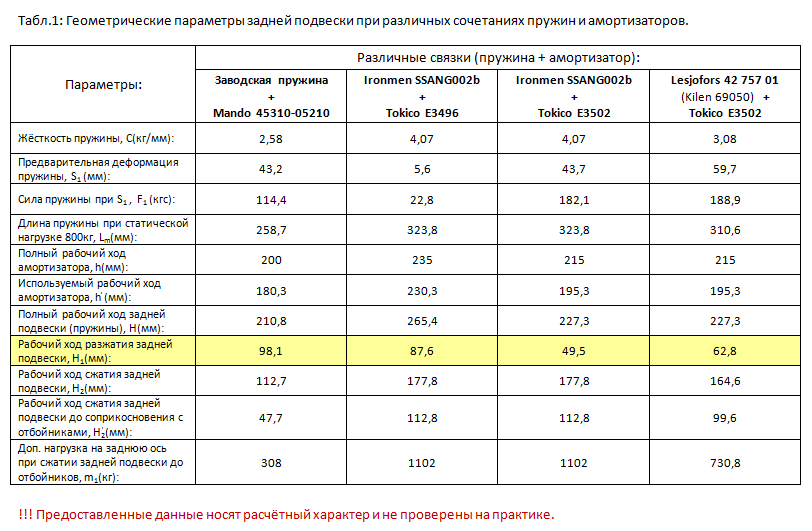
Допускается применение для подвесок автомобилей семейства LADA Samara.
Заказ обратного звонка
Пружины сжатия: на что следует обратить внимание при проектировании пружин
Примечания к конструкции
(1) Характеристики пружин сжатия
Рис. 2 Форма конца пружины сжатия
(3) Боковая жесткость пружин сжатия
Постоянство пружины в вертикальном и горизонтальном направлениях
Если центральная линия витка ориентирована вертикально, а направление, перпендикулярное ей, по горизонтали жесткость пружины в вертикальном направлении определяется выражением (1).
В этом случае жесткость пружины в горизонтальном направлении называется поперечной жесткостью и может быть получена с помощью выражения (2).
Жесткость пружины в вертикальном направлении
Жесткость пружины в горизонтальном направлении
ky=выражение (1)=P/δs
kx：поперечная жесткость
hs：высота пружины при вертикальной нагрузке P=h0-δs
C : коэффициент, определяемый аспектным отношением и (вертикальный прогиб / свободная высота)
Как видно из выражения (1), если форма пружины известна, значение ky можно определить однозначно. С другой стороны, необходимо помнить, что боковая жесткость зависит от вертикального отклонения пружины.
В любом случае, если требуются kx и ky, их можно рассчитать путем деления прогиба пружины, вызванного наклонной нагрузкой в произвольном направлении, на вертикальную и горизонтальную составляющие.
Рис.4
Может ли пружина сжатия также действовать на моменты?
Пружина сжатия также может воздействовать на моменты.
Это свойство используется в рессорах подвески легковых автомобилей, где пружины встроены в рычажные механизмы, как показано на рис.5. Здесь к пружине приложен момент помимо вертикальной и горизонтальной нагрузок. На рис.6 показано состояние, когда пружина сжатия сжата на высоту h опорными пластинами, наклоненными на углы φ1 и φ2.
А момент М1(6) и М2(7)
Q = выражение (4)
q = выражение (5)
Момент M1 = выражение (6)
Момент M2 = выражение (7)
(4) О пульсации пружин сжатия
Когда на пружину воздействуют синусоидальные вынужденные колебания, помпаж формирует стационарную волну.
Когда соотношение между частотой f внешней силы и собственной частотой f1
пружины удовлетворяет уравнению (a), возникает явление резонанса, называемое помпажем.
Здесь первая собственная частота f1 определяется следующим уравнением.
(b)
На практике синусоидальные вынужденные колебания возникают редко. Как правило, вынужденное смещение y задается как функция времени.
Когда скорость вращения распределительного вала ω постоянна, как в клапанных пружинах современных двигателей, кривая подъема клапана y(t) представлена рядом Фурье, как показано ниже.
Когда пружина находится в первичном резонансном состоянии с волновым сознаком n-го порядка (nωt + φn), максимальное пульсирующее напряжение τs, создаваемое в пружине, является тем же напряжением τs (t), которое возникает, когда пружина статически сжимается только до y(t). Это напряжение определяется следующим уравнением. (d)
Здесь b – коэффициент демпфирования. Это зависит от сложных факторов и не может быть определено безоговорочно, но обычно используется значение от (b) до (d).
Рис.7. Изменение напряжения из-за помпажа
На рис. 7 показана диаграмма напряжения пружины клапана при возникновении помпажа.
τ1 на рисунке – напряжение, вызванное начальным сжатием пружины в закрытом положении клапана. Минимальное значение напряжения τmin и максимальное значение напряжения τ2 в это время можно рассчитать по уравнениям (e) и (f) соответственно.
(e)(f)
Диапазон изменения напряжения τr определяется уравнением (g).
(ж)
Пример резонансной кривой, полученной при испытании на колебания пружины клапана, показан на рис.8. Эта кривая представляет собой зависимость амплитуды колебаний центральной катушки пружины клапана от скорости вращения распределительного вала. Пики на рисунке представляют собой резонансные колебания, возникающие, когда собственная частота пружины клапана совпадает с верхней гармоникой кривой подъема клапана. Высоты пиков непостоянны, поскольку непостоянны амплитуды гармоник cn.
Например, поскольку пик #10, соответствующий 10-й верхней гармонике, возникает при частоте вращения распределительного вала 1200, собственная частота испытанной пружины клапана составляет 10×(1200/60)=200 имп/с=12000 имп/мин.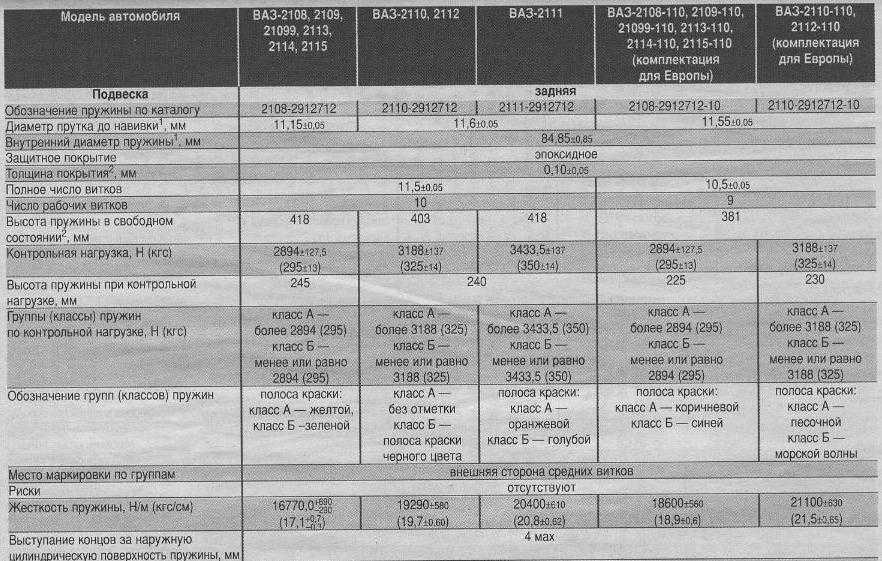
Для предотвращения помпажа можно рассмотреть следующие методы.
Рис. 8. Пример кривой резонанса пружин клапана
Как правило, трудно предотвратить резонанс пружины на всех гармониках кривой подъема клапана в диапазоне изменения частоты вращения двигателя.
Однако, как можно предположить из рис.8, поскольку амплитуда верхних гармоник уменьшается с увеличением порядка гармоники, неизбежно уменьшается и резонансное колебание. Поэтому, если собственную частоту пружины сделать максимально возможной, чтобы резонанс возникал только на высших гармониках, это может значительно снизить эффект помпажа. Однако следует соблюдать осторожность, поскольку высокая собственная частота имеет тенденцию увеличивать напряжение из-за начального сжатия.
Изменение формы кулачков
Например, если установить низшую собственную частоту клапанной пружины для двигателей с частотой вращения в диапазоне 2000-3000 об/мин 500 гц, то она будет резонировать на 10-15 гармониках.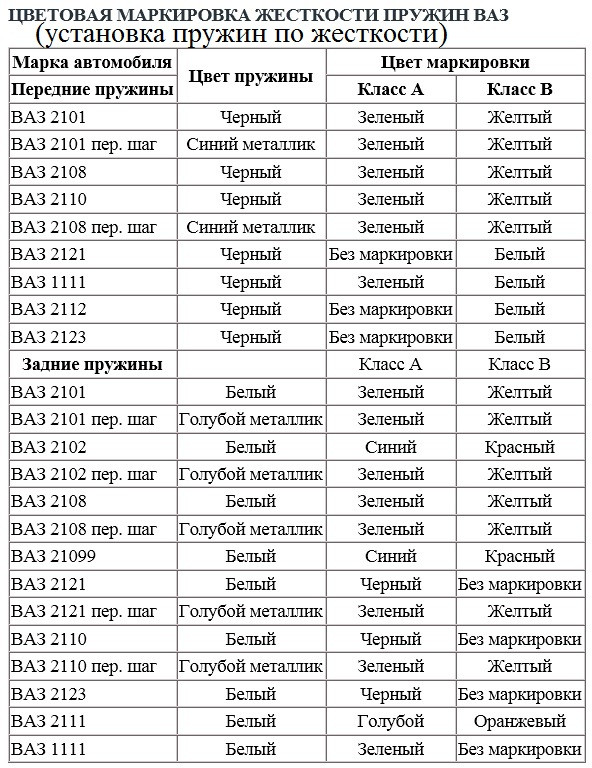
Поэтому достаточно сконструировать кулачки так, чтобы амплитуда этих гармоник была небольшой.
Используйте пружины с нелинейными характеристиками
Поскольку собственная частота нелинейных винтовых пружин сжатия зависит от прогиба, это может предотвратить явление резонанса на высших гармониках.
(5) Радиальная нагрузка (боковая нагрузка)
В цилиндрических пружинах сжатия, если сила сжатия приложена к двум параллельным концам пружин, диаметр пружины изменяется в соответствии с приложенным давлением, вызывая смещение оси вертикальной нагрузки немного не по центру. Этот эффект вызывает радиальную нагрузку (поперечную нагрузку) пружин сжатия.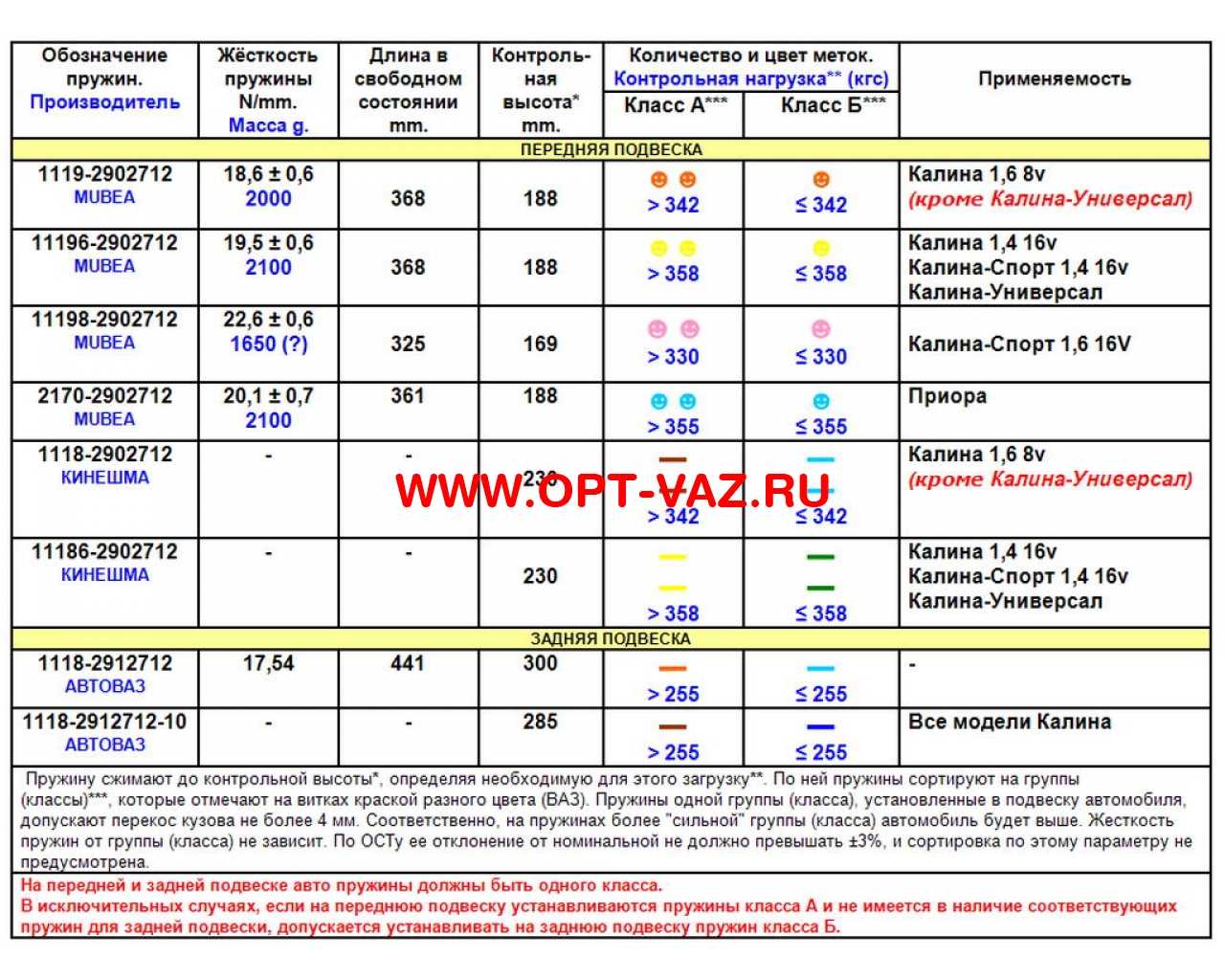
(6) Прочие соображения
а. Индекс пружины
Когда индекс пружины становится маленьким, локальное напряжение становится чрезмерным, а когда индекс пружины становится большим или малым, работоспособность пружины становится проблемой. Поэтому индекс пружины предпочтительно выбирать в диапазоне от 4 до 15 для горячедеформированных пружин и от 4 до 22 для холоднодеформированных пружин.
б.
Соотношение сторон
Соотношение сторон (соотношение высоты в свободном состоянии и среднего диаметра рулона：
) устанавливается равным 0,8 или более, чтобы закрепить несколько активных рулонов, и с учетом коробления обычно предпочтительно выбирать в диапазоне 0,8 к 4.
в. Количество активных витков
Если количество активных витков меньше 3, характеристики пружины будут нестабильными, поэтому предпочтительно установить количество активных витков на 3 или более.
д. Шаг
Если шаг превышает 0,5 D, то диаметр витка обычно изменяется при увеличении прогиба (нагрузки). Следовательно, необходимо скорректировать прогиб и напряжение кручения, полученные из базовой формулы, поэтому 0,5 D или меньше считается подходящим шагом.
Шаг обычно оценивается по следующей приблизительной формуле.
Учебное пособие по линейным и нелинейным пружинам
Справочные материалы
Введение
В этом учебном пособии представлен основной обзор линейных и нелинейных пружин и связанных с ними уравнений для силы, жесткости и потенциальной энергии.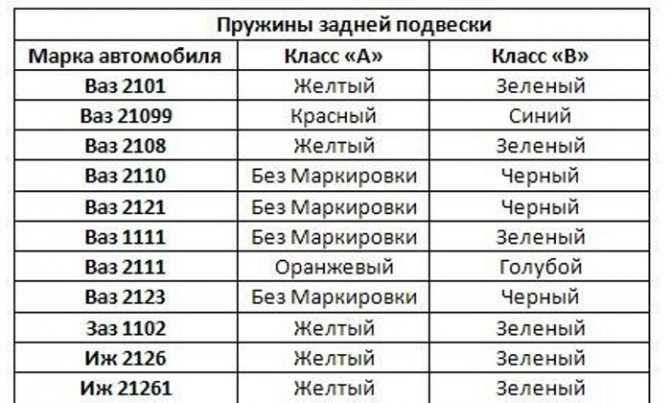
Вам понадобятся базовые знания исчисления (интегралы и производные), чтобы понять раздел о нелинейных пружинах.
Определения
Линейная пружина имеет линейную зависимость между силой и смещением, что означает, что сила и смещение прямо пропорциональны друг другу. График, показывающий зависимость силы от смещения для линейной пружины, всегда будет прямой линией с постоянным наклоном.
Нелинейная пружина имеет нелинейную зависимость между силой и смещением. График, показывающий зависимость силы от смещения для нелинейной пружины, будет сложнее, чем прямая линия с изменяющимся наклоном.
Краткий обзор уравнений
Кредиты
Автор: Ben Finio, Ph.D., Science Buddies
Линейные пружины
Если вы когда-либо слышали о пружинах на уроках физики или где-либо еще, этот символ может быть вам знаком:
Символ на рис. 1 выше выглядит как типичная «свернутая» металлическая пружина (см. рис. 2). В реальной жизни пружины бывают всех форм и размеров.
Однако другие объекты, такие как резиновые ленты, также могут действовать как пружины.
Наряду с символом на рисунке 1 вы могли видеть это уравнение:
Уравнение 1: [Пожалуйста, включите JavaScript для просмотра уравнения]
Это уравнение моделирует базовую физику пружины — оно описывает, как пружина проявляет силу, когда вы нажимаете или тянете ее. Сила ( F ) (в ньютонах) пропорциональна смещению ( x ) (в метрах) пружины — и сила рассчитывается путем умножения смещения на постоянную пружины ( k ) (в ньютонах/метр). Вы также можете услышать константу пружины, называемую
Уравнение 2: [Пожалуйста, включите JavaScript для просмотра уравнения]
(где x — текущая длина пружины, а x 0 — длина пружины в нейтральном положении)
или:
Уравнение 3: [Пожалуйста, включите JavaScript для просмотра уравнения]
(где Δx — разница между текущей длиной пружины и ее нейтральной длиной).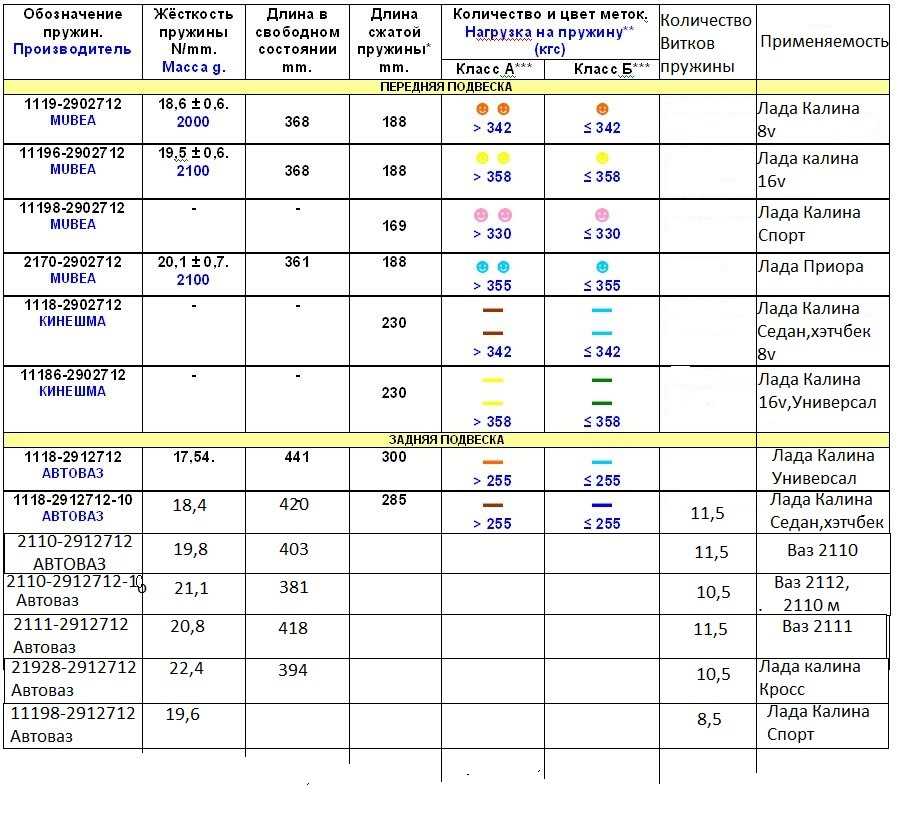
Уравнения 1, 2 и 3 означают одно и то же — вам просто нужно следить за тем, как вы определяете x .
Если мы возьмем уравнение 1 и используем его для построения кривой зависимости силы от смещения для пружины (возьмем k = 100 Н/м), мы получим график на рисунке 3 ниже. Обратите внимание, что кривая зависимости усилия от смещения представляет собой прямую линию, поэтому мы называем это линейной пружиной 9.0157 . Также обратите внимание, что мы можем изменить уравнение 1:
уравнение 4: [Пожалуйста, включите JavaScript для просмотра уравнения]
Перестановка в уравнении 4 говорит нам о том, что k — это наклон линии на рис. состоит в том, чтобы подвесить грузы к пружине и измерить ее смещение с помощью линейки), и полученная кривая выглядит линейной, вы можете использовать уравнение 4 для расчета жесткости пружины. Если полученная кривая равна
Вы также можете быть знакомы с уравнением для потенциальной энергии (или PE ), хранящейся в пружине:
Уравнение 5: [Пожалуйста, включите JavaScript для просмотра уравнения]
, где опять же, в зависимости от метода выражения переменной x , это также может быть записано как:
Уравнение 6: [Пожалуйста, включите JavaScript для просмотра уравнения]
или:
Уравнение 7: [Пожалуйста, включите JavaScript для просмотра уравнения]
Но откуда взялось это уравнение? Мы покажем вам, как прийти к уравнению 5 двумя способами — с исчислением и без него.
Без вычислений
Для линейных пружин можно рассчитать потенциальную энергию без вычислений. Для этого нам понадобится другое обычное физическое уравнение:
Уравнение 8: [Пожалуйста, включите JavaScript для просмотра уравнения]
Это уравнение говорит, что работа (или Вт ) (в джоулях), совершаемая силой (или F ), равна произведению этой силы на расстояние ( d ), над которыми он действует.
Это также означает, что вы можете рассчитать полную проделанную работу и, следовательно, потенциальную энергию, рассчитав площадь 90 156 под кривой сила-перемещение 90 157 — именно это мы имеем на рис. 3! Мы знаем, что площадь под кривой силы-перемещения для линейной пружины всегда будет прямоугольным треугольником, а площадь прямоугольного треугольника равна:
Уравнение 9: [Пожалуйста, включите JavaScript для просмотра уравнения]
Итак, для линейной пружины имеем:
Уравнение 10: [Пожалуйста, включите JavaScript для просмотра уравнения]
и вот оно! Вот как вы пришли к уравнению 5. Рисунок 4 ниже помогает проиллюстрировать, как вы вычисляете площадь.
С исчислением
Если вы знакомы с исчислением, то вы, вероятно, понимаете, что все, что мы сделали в предыдущем разделе, — это взяли частный случай интеграла — в данном случае площадь треугольника.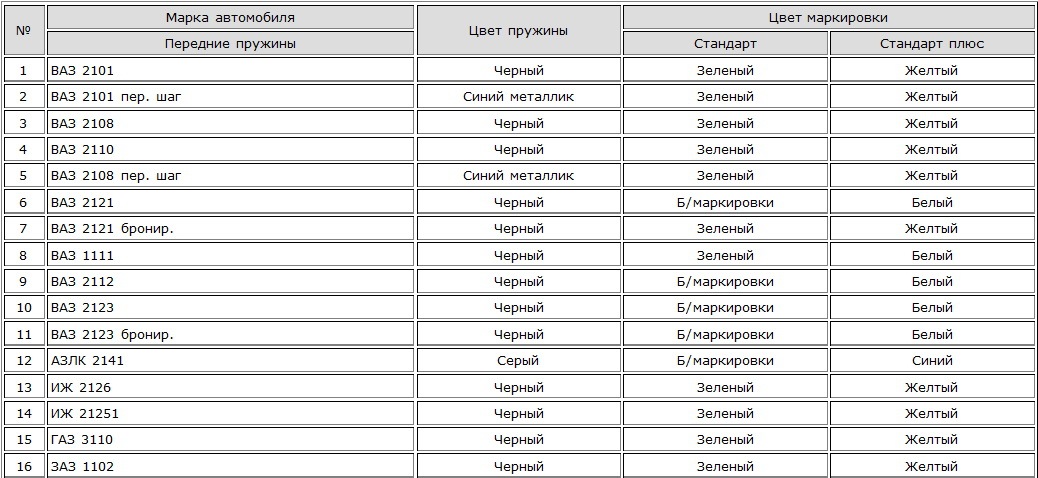
В более общем смысле мы хотим интегрировать уравнение 8, чтобы получить накопленную потенциальную энергию (это будет полезно в разделе о нелинейных пружинах). Значит, работа переменной силы F(u) на расстоянии x равно:
Уравнение 11: [Пожалуйста, включите JavaScript для просмотра уравнения]
, где u — это фиктивная переменная, которую мы вставили для расстояния (помните, что использование одной и той же переменной как для пределов интеграла, так и внутри интеграла считается плохой математической формой — это может вызвать у вас проблемы с вашим учителем математики !). Если мы подставим уравнение 1 сверху в уравнение 11 и заменим W с PE (это можно сделать, так как при отсутствии потерь на трение работа, необходимая для растяжения пружины, будет в точности равна результирующей потенциальной энергии, запасенной в пружине), определяем, что:
Уравнение 12: 90 157
[Пожалуйста, включите JavaScript для просмотра уравнения]
и снова мы пришли к уравнению 5!
Нелинейные пружины
В предыдущем разделе речь шла о линейных пружинах, которые следуют простому набору уравнений и ведут себя «хорошо».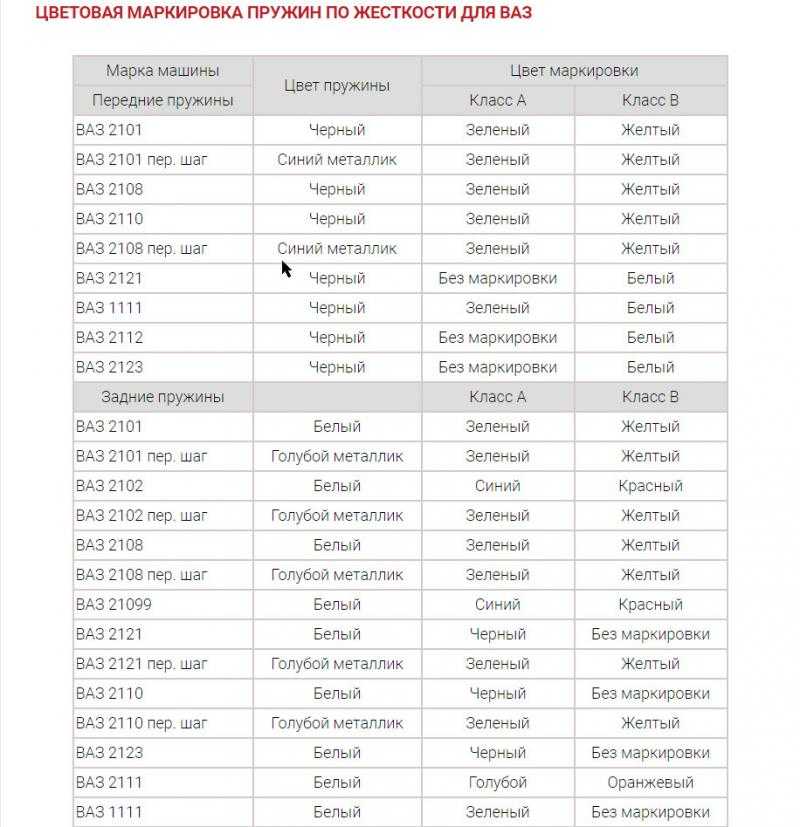
Однако в реальной жизни пружины могут вести себя не так. Например, на рисунке 5 показана кривая сила-перемещение, которую мы измерили для
резинка в проекте Science Buddies,
Время запуска: физика движения снаряда катапульты.
Вы видите проблему? Это не прямая линия. Это означает, что резинка не подчиняется уравнению 1 (в разделе «Линейные пружины», где F=kx ) для силы как функции смещения — и, следовательно, оно не будет следовать уравнению 5 (в разделе «Линейные пружины», где PE=1/2 k x² ) для потенциальной энергии. Резинка ведет себя как нелинейная пружина . Мы можем использовать инструмент подбора кривой, чтобы найти уравнение для линии. В этом случае уравнение для данных на Рисунке 5:
Уравнение 13: [Пожалуйста, включите JavaScript для просмотра уравнения]
Как и в разделе «Линейные пружины», F — сила в ньютонах, а x — смещение пружины от нейтрального положения в метрах.
Значения 33,55 и 0,4871 характерны для резиновой ленты из нашего проекта катапульты, поэтому мы можем написать более общую форму этого уравнения с двумя константами, a и p , где a — коэффициент, а p — показатель степени:
Уравнение 14: [Пожалуйста, включите JavaScript для просмотра уравнения]
Этот тип уравнения называется степенным законом , потому что переменная x возведена в степень p . Значения a и p будут разными для разных резинок. Однако, , вы не можете всегда предполагать, что нелинейная пружина будет подчиняться степенному закону! Так случилось и в эксперименте с катапультой — существуют другие потенциальные уравнения для кривой зависимости силы от смещения, такие как экспоненциальная , полином или логарифм . У нас нет места для объяснения этих различных типов кривых здесь — дело в том, что вы всегда должны проводить эксперимент, чтобы создать кривую зависимости усилия от смещения для вашей пружины, а затем выяснять, какой тип кривой лучше всего соответствует данным.
Теперь обратите внимание, чем вышеприведенное уравнение 14 отличается от уравнения 1 в разделе «Линейные пружины». Поскольку у нас есть нелинейная пружина, наклон кривой сила-смещение не является постоянным. определение k как «наклон кривой силы-перемещения» по-прежнему верно, но теперь это значение может измениться. В общем, вы можете взять производную кривой сила-перемещение в любой точке, чтобы найти жесткость (мы больше не называем ее «пружинной константой», потому что на самом деле она не является константой):
Уравнение 15 : [Пожалуйста, включите JavaScript для просмотра уравнения]
Для резинки в нашем проекте мы собираемся округлить показатель степени p до ½. Затем мы можем подставить уравнение 13 в уравнение 15, и мы придем к нашему уравнению для жесткости резиновой ленты:
Уравнение 16: [Пожалуйста, включите JavaScript для просмотра уравнения]
На рис.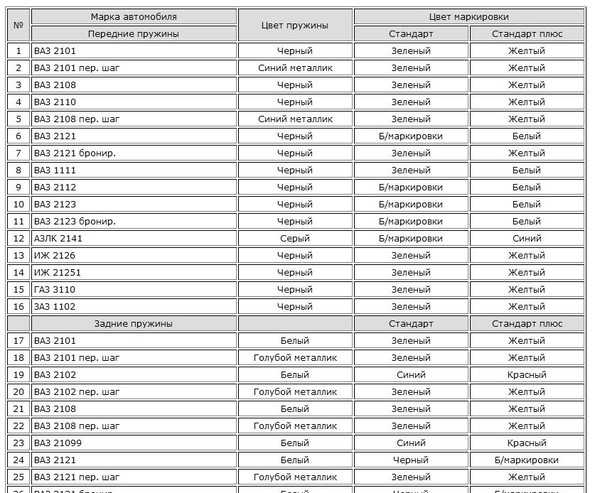
6 показана кривая зависимости жесткости от смещения для этой конкретной резиновой ленты. Обратите внимание, как по мере того, как резинка растягивается сильнее, жесткость уменьшается, а не остается постоянной. Это означает, что резинка на самом деле получает слабее по мере растяжки.
Мы также хотим рассчитать потенциальную энергию этой нелинейной пружины. Мы можем использовать общее уравнение:
Уравнение 17: [Пожалуйста, включите JavaScript для просмотра уравнения]
Помните, что PE — это потенциальная энергия, а u — это фиктивная переменная, которую мы используем для перемещения, поскольку мы уже используем x 9.0185 для предела интеграла. В случае нашей резинки это оценивается как:
Уравнение 18: [Пожалуйста, включите JavaScript для просмотра уравнения]
Обратите внимание, что это сильно отличается от уравнения 5 (из раздела «Линейные пружины»).