Технические характеристики Toyota RAV4 XA50 (2019-2020)
В октябре 2019 года на российском рынке стартовали продажи пятого поколения кроссовера Toyota RAV4. Модель в кузове XA50, как оказалось, довольно сильно отличается от предыдущей версии XA40 не только в плане дизайна и комплектации, но и в технической части. Во-первых, новинка построена на новой платформе TNGA K, которая позволила увеличить жесткость силового каркаса, снизить центр тяжести и оптимизировать распределение массы по осям. Во-вторых, автомобиль 5-го поколения оснащается принципиально новыми силовыми агрегатами из семейства Dynamic Force. В-третьих, у новой модели РАВ4 нет полноприводных модификаций с механической коробкой и нет дизельных версий.
Toyota RAV4 2.0 149 л.с.
Базовым двигателем для нового Рафика стал 2.0-литровый бензиновый атмосферник с заводским индексом M20A-FKS. Он относится к новой линейке Dynamic Force Engines, включающей передовые моторы Тойота с высоким термическим КПД 40%. Четырехцилиндровый агрегат получил алюминиевый блок с вплавленными гильзами, газораспределительный механизм DVVT-iE с изменением фаз на впуске (VVT-iE) и выпуске (VVT-i), систему комбинированного впрыска топлива (распределенный впрыск сочетается с непосредственным).
Конструктивные особенности мотора – лазерная насечка на юбках поршней для лучшего удержания масла, близкое расположение каналов для ОЖ и масла (ускоряется прогрев), гидрокомпенсаторы и роликовые толкатели в клапанных группах, цепной привод ГРМ с гидронатяжителем. Двигатель работает по циклу Миллера, геометрическая степень сжатия 13.0:1.
Двигатель 2.0 M20A-FKS
Кроссовер с 2.0-литровым мотором M20A-FKS, выдающим 149 л.с. и 206 Нм, оснащается либо 6-ступенчатой МКПП, либо вариатором. Во втором случае привод может быть как передним, так и полным. У вариатора первая и задняя передачи механические.
Toyota RAV4 2.5 199 л.с.
Двигатель A25A-FKS объемом 2.5 литра конструктивно мало чем отличается от «младшего» агрегата M20A-FKS. Максимальная мощность силовой установки составляет 199 л.с. (при 6600 об/мин), крутящий момент достигает 243 Нм (в диапазоне 4000-5000 об/мин). В связке с мотором работает новый 8-ступенчатый «автомат», привод у такой модификации исключительно полный.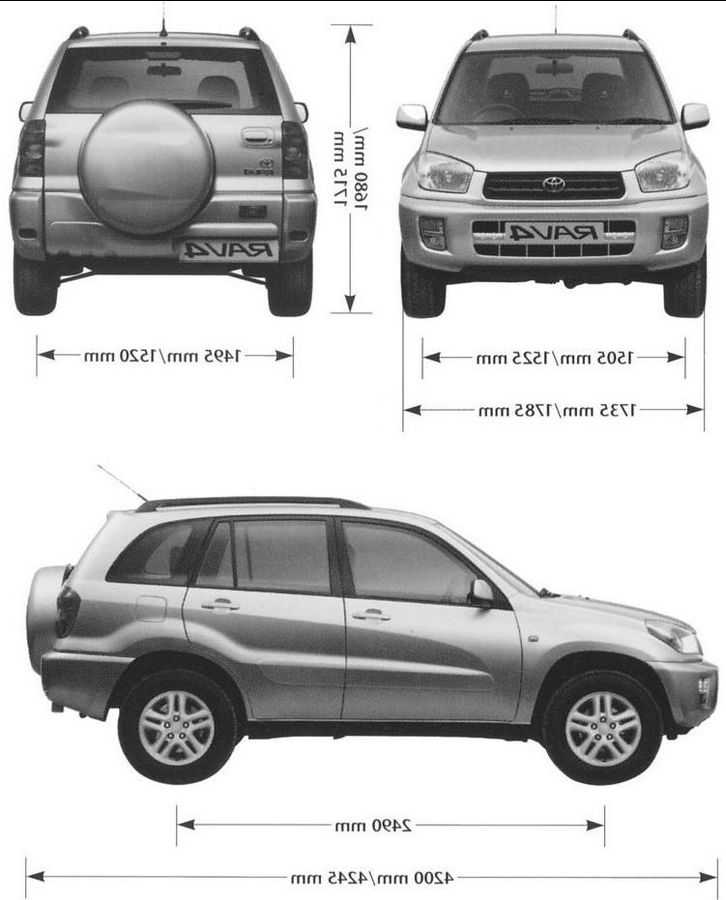
Двигатель 2.5 A25A-FKS
Dynamic Torque Vectoring AWD
Схема полного привода нового Тойота РАВ 4 в дорогих комплектациях Престиж и Престиж Safety принципиально отличается от классической конфигурации Dynamic Torque Control AWD. Здесь нет ни межосевой муфты, ни заднего дифференциала. Изначально кроссовер является переднеприводным, а назад тяга направляется с помощью раздаточной коробки, карданного вала и редуктора с двумя электромеханическими многодисковыми муфтами (у каждого колеса своя). С обеих сторон кардана установлены кулачковые муфты с электромагнитами – при их размыкании передача потока мощности на заднюю ось прекращается, сам вал перестает крутиться.
Распределением момента в трансмиссии Dynamic Torque Vectoring заведует специальный блок управления, расположенной в кормовой части автомобиля. Он учитывает множество параметров, в том числе, положение рулевого колеса, частоту вращения колес, угловое ускорение, положение педали тормоза, выбранную передачу.
На основании полученных данных ЭБУ дозирует тягу на задних колесах, причем передаваемое усилие определяется исключительно силой тока на электромагнитах.
За изменение режима работы новой системы полного привода Тойота РАВ 4 ХА50 отвечает трехпозиционный переключатель Multi-Terrain Select. Он позволяет выбирать между настройками Normal (Нормальный), Mud & Sand (Грязь и песок) и Rock & Dirt (Камни и грунт). Два последних режима активируются на скоростях до 40 и 25 км/ч соответственно.
Полные технические характеристики Тойота РАВ 4 (кузов ХА50)
Четыре измерения
Четыре измерения| ГЭС 0410 | Эйнштейн для всех | |
Назад на страницу основного курса
Джон
Д. Нортон
Кафедра истории и философии науки
Университет Питтсбурга
- Одномерный интервал
- Двумерный квадрат
- Трехмерный куб
- Четырехмерный куб: тессеракт
- Стереовидение
- Сводная таблица
- Вместительный вызов
- Запутанный вызов
- Использование цветов для визуализации дополнительного измерения
- Что вы должны знать
Мы уже видели, что нет ничего страшного
таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время.
Моя текущая цель — показать вам, что в
все таинственное в четырех измерениях пространства-времени. Для этого я брошу
временная часть полностью. Я просто рассмотрю четырехмерный
пространство; то есть пространство точно такое же, как наше трехмерное пространство, но с
одно дополнительное измерение. Каково это?
Без всяких усилий я могу визуализировать трехмерное -мерное пространство — и вы тоже можете. Что бы это
быть как жить в трехмерном кубе? Чтобы его попросили визуализировать
это как просят дышать или моргать.
| Могу ли я представить, каково было бы жить в четырехмерный аналог куба, четырехмерный куб или «тессеракт»? Я не могу представить это с таким же легким непосредственность. Сомневаюсь, что и вы сможете. Но это только о единственное, что мы не можем сделать. В противном случае мы можем определить все свойства тессеракта и то, что это будет нравится жить в одном. Для этого существует множество техник. я покажет вам один ниже. Он включает в себя продвижение через последовательность измерений, экстраполируя естественные выводы в каждом шагнуть в четвертое измерение. Как только вы видели, как это делается для особого случая тессеракта у вас не будет проблем применяя его к другим случаям. |
Дверь в четвертое измерение открывается.
Одномерный интервал
Одномерным аналогом куба является интервал. это
формируется путем взятия безразмерной точки и ее перетаскивания на определенное расстояние.
Это расстояние может быть 2 дюйма или 3 фута или что-то еще. Давайте позвоним
расстояние «Л».
Интервал имеет длину L. Он ограничен двумя точками как его грани — две точки на обоих концах интервала.
Двумерный квадрат
Двумерным аналогом куба является квадрат. это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.
Квадрат имеет площадь L 2 . Он ограничен гранями
на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре.
их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.
Итак, у нас есть 2 измерения x 2 грани в каждой = 4 грани.
грани вместе образуют периметр длиной 4xL.
Трехмерный куб
Чтобы сформировать куб, мы берем квадрат и перетаскиваем его на расстояние L в третьем измерении.
Объем куба L 3 . Он ограничен гранями на 6 сторон. Грани представляют собой квадраты площадью L 2 . Мы знаем, что есть 6 из них, так как его трехмерные оси должны быть закрыты с обоих концов лица.
Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами. На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.
Четырехмерный куб: тессеракт
Пока я надеюсь, что вы нашли наши конструкции полностью
безупречный.
Следующий шаг в четыре измерения можно сделать одинаково
механически. Мы просто систематически повторяем каждый шаг выше. Единственный
разница в том, что на этот раз мы не можем легко сформировать ментальную картину
что мы строим. Но мы можем знать все его свойства!
Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его
расстояние L в четвертом измерении . Мы не можем точно представить
как это выглядит, но это примерно так:
Тессеракт имеет объем L 4 . Он ограничен
грани с 8 сторон. Грани представляют собой кубы объема L 3 . Мы знаем
их 8, так как его четыре оси должны быть ограничены
любой конец гранями — две кубические грани на ось. Еще раз, мы не можем
визуализируйте все четыре из этих закрытых измерений. Мы можем в лучшем случае визуализировать
три направления перпендикулярны друг другу. Затем мы каким-то образом добавим в
четвертый (красный):
Итак, у нас есть 4 измерения по 2 грани в каждой = 8 граней.
Есть несколько способов сделать рисунок, который
соответствует взгляду на тессеракт под разными углами. Фигура
показывает два способа сделать это. Первый дает косой обзор; секунда
смотрит по одной из осей.
Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL 3 ).
Стереовидение
«Чертежи» тессеракта плохо видны.
Это потому, что они действительно должны быть трехмерными моделями в
трехмерное пространство.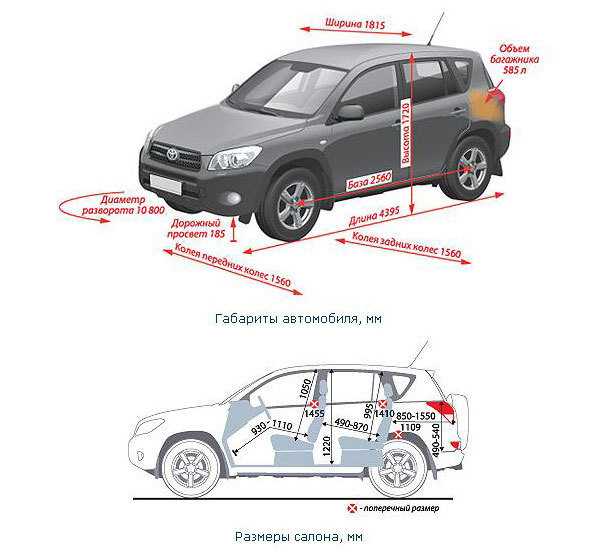
Изображения ниже представляют собой стереопары. Если вы знакомы
с тем, как их просматривать, вы увидите, что они дают вам хороший стереофонический вид
трехмерной модели. Если это новое для вас, они берут
практика, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не смотрит на
левое изображение и правый глаз смотрит на правое изображение.
Но как научиться этому? мне проще всего
начать, если я сижу далеко от экрана и смотрю вдаль
над верхней частью экрана. Я вижу два несколько размытых изображения на
край моего поля зрения. Пока я не сосредотачиваюсь на них, они начинают
дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют
вместе тем лучше. Я стараюсь усилить дрейф, насколько это возможно, пока
осторожно перемещая свой взгляд к изображениям.
Эту пару легче сплавить:
и этот немного сложнее:
Сводная таблица
Мы можем подытожить развитие свойств
tesseract следующим образом:
| Размер | Фигурка | Лицо | Том | Номер лиц | Том поверхность/периметр |
|---|---|---|---|---|---|
| 1 | интервал | точка | л | 1×2=2 | два очки |
| 2 | квадрат | интервал | л 2 | 2×2=4 | 4 л |
| 3 | куб | квадрат | л 3 | 3×2=6 | 6 л 2 |
| 4 | тессеракт | л 4 | 4×2=8 | 8 л 3 |
Вместительный вызов
Если бы вы жили в тессеракте, вы могли бы выбрать
жить на своей трехмерной поверхности, как двухмерный человек
могли бы выбрать жить в 6 квадратных комнатах, которые образуют двухмерный
поверхность куба.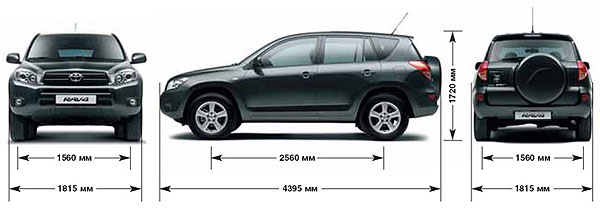
Таким образом, ваш дом будет состоять из восьми кубов, образующих поверхность.
из тессеракта. Представьте себе, что есть двери, где когда-либо две из
эти кубики встречаются. Если вы находитесь в одной из этих комнат, сколько дверей будет
Понимаете? Как бы выглядела следующая комната, если бы вы прошли через одну из
двери? Через сколько дверей нужно пройти, чтобы добраться до самой дальней
номер? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт?
Некоторые из этих вопросов непростые. Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы на тессеракт.
Запутанный вызов
Доступ к четвертому измерению делает возможным многое
иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать
стратегия обдумывания процесса в трехмерном пространстве.
затем
мы воспроизвели его в четырехмерном пространстве.
Рассмотрим монету, лежащую в рамке на столе.
Монета не может быть удалена из рамки в пределах ограничивает двумерную поверхность стола. Теперь вспомните что у нас есть доступ к третьему измерению. Монета легко удалить, просто подняв его в третье измерение, высота над столом. После этого мы можем передвигать монету по своему усмотрению в более высокую слой, а затем опуститься обратно на столешницу за пределами рамы. |
При подъеме следует обратить внимание на то, что движение
вообще не двигает монету в двух горизонтальных направлениях двух
объемное пространство. Таким образом, движение никогда не приближает его к кадру и там
нет опасности столкновения с рамой.
| Теперь повторите этот анализ для его аналог в одном более высоком измерении, мрамор запертым в трехмерном ящике. |
| |
| Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве. Мы можем разделить их, используя доступ к четвертому измерению? |
Это можно сделать точно так же
процесс подъема одного из колец в четвертое измерение. В качестве
прежде обратите внимание, что подъем не перемещает кольцо ни в одном из
три направления трехмерного пространства, удерживающие
первоначально связанные кольца. Так что движения рисков нет
столкновения перемещаемого кольца с другим. Подъем просто
поднимает перемещенное кольцо на новый трехмерный слой из четырех
размерное пространство, в котором нет ни одной части другого кольца. перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы
с удовольствием опустился обратно в исходное трехмерное пространство в
совсем другое место. |
А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке. Некоторые узлы просто кажущиеся клубки, которые могут довольно легко разойтись. Остальные настоящие и можно расстегнуть, только продев конец веревки в петлю. Так примите это за настоящий узел: тот, который не может быть развязаны любыми манипуляциями с веревкой, если мы не сможем ухватиться за заканчивается. (Представьте, если хотите, что каждый из них прикреплен к стене и нельзя удалить.)
Задача состоит в том, чтобы убедить
сами понимаете, что в четырехмерном пространстве на веревках нет настоящих узлов.
пространство. Основная помощь, которая вам понадобится, — это описанная выше манипуляция с
связанные кольца.
Для начала представьте, как бы вы использовали четвертый
измерение, чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.
Использование цветов для визуализации дополнительных размер
Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства может быть представлено различия цветов.
Вот как это работает, когда мы начинаем с двухмерного пространства и подняться в третье измерение. Объекты в оригинале два мерное пространство черное. Когда мы поднимаемся через третий измерения, они последовательно приобретают синий цвет, зеленый и красный. |
Теперь давайте применим этот цветной слой. трюк к более раннему примеру подъема монеты из рамки.
монета начинается в том же двухмерном пространстве, что и рамка. Мы поднимаем
это в третье измерение в более высокое
пространственный слой, который мы закодировали красным цветом. В этом высшем
слой, монета может свободно перемещаться влево/вправо и вперед/назад без
пересекающие рамку. Мы перемещаем его вправо, пока он не пройдет
над рамой. Затем опускаем обратно вниз снаружи. |
А теперь представьте, что мы не можем
воспринимать третье измерение напрямую. Вот как мы
представить побег монеты. Он начинается внутри кадра в
пространство кадра. Затем он поднимается из рамы в
третье измерение. В этот момент на это указывает призрачный
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. мы этого не увидим
однако перемещайтесь по кадру. Насколько нам известно, это будет
просто пройди через это.Движение монеты в этом трехмерном побеге иллюстрируется призрачным красным монета. |
Этот последний анализ монеты в
кадр является шаблоном для работы с
реальный случай шарика, заключенного в трехмерную коробку. Если
шарик движется в любом из трех известных измерений (вверх/вниз,
влево/вправо и вперед/назад), его движение пересекает стены
ящик, и он не может убежать. Итак, мы поднимаем шарик в четвертый
измерение, не меняя своего положения в трех привычных
Габаритные размеры. На рисунке это показано тем, что мрамор становится призрачным.
красный. В красном поле шарик может двигаться вверх/вниз,
слева/справа и спереди/сзади, не пересекая стенки коробки.
Затем мрамор перемещается так, что проходит над одной из стен. это
затем опустили из красного пространства обратно к исходным трем
мерное пространство коробки, но уже вне стен. |
| То же анализ относится к связанным кольцам. Одно кольцо снято из трехмерного пространства исходной установки. В этом красное пространство, кольцо может свободно двигаться, не пересекаясь с другим звенеть. Мы отодвигаем его подальше от другого кольца, а затем опускаем обратно. в исходное трехмерное пространство. Теперь он не связан с другое кольцо. |
Что следует знать
- Свойства квадратов, кубов и тессерактов.
- Как получить свойства тессеракта и других четырехмерные фигуры путем экстраполяции методов, используемых для получения свойства куба.
Авторское право Джон Д. Нортон. февраль 2001 г.;
июль 2006 г., 2 февраля 2008 г.; 6 февраля 2012 г.; 30 апреля 2014. Январь
30, 2022.
Наша Вселенная может иметь пятое измерение, которое изменит все, что мы знаем о физике. мы живем во Вселенной с четырьмя измерениями пространства-времени. Однако для повседневных целей мы представляем Вселенную в трех измерениях пространства (север-юг, восток-запад, верх-низ) и одном измерении времени (прошлое-будущее). В этом случае пятое измерение было бы дополнительным измерением пространства.
Такое измерение было независимо предложено физиками Оскаром Кляйном и Теодором Калузой в 1920-х годах. Они были вдохновлены теорией гравитации Эйнштейна, которая показала, что масса искажает четырехмерное пространство-время.
Поскольку мы не можем воспринимать эти четыре измерения, мы приписываем движение в присутствии массивного тела, такого как планета, не этой кривизне, а «силе» гравитации.
Можно ли объяснить другую известную в то время силу (электромагнитную силу) искривлением дополнительного измерения пространства?
Калуца и Кляйн обнаружили, что можно. Но поскольку электромагнитная сила была в 1040 раз сильнее гравитации, кривизна дополнительного измерения должна была быть настолько велика, чтобы оно было свернуто намного меньше атома и его было бы невозможно заметить. Когда такая частица, как электрон, путешествует в невидимом для нас пространстве, она будет вращаться по пятому измерению, как хомяк в колесе.
Больше похоже на это
Пятимерной теории Калуцы и Клейна был нанесен серьезный удар открытием еще двух фундаментальных взаимодействий, действующих в области атомного ядра: сильного и слабого ядерных взаимодействий.
Но идея о том, что дополнительные измерения объясняют силы, была возрождена спустя полвека сторонниками «теории струн», которая рассматривает фундаментальные строительные блоки Вселенной не как частицы, а как крошечные «струны» массы-энергии.
Чтобы имитировать все четыре силы, струны вибрируют в 10-мерном пространстве-времени, где шесть свернутых пространственных измерений намного меньше атома.
Теория струн породила идею о том, что наша Вселенная может быть трехмерным островом или «браной», плавающей в 10-мерном пространстве-времени. Это открыло интригующую возможность объяснить, почему гравитация так необычайно слаба по сравнению с тремя другими фундаментальными силами. Согласно этой идее, в то время как силы прикованы к бране, гравитация просачивается в шесть дополнительных пространственных измерений, чрезвычайно ослабляя свою силу на бране.
Существует способ иметь большее пятое измерение, искривленное таким образом, что мы его не видим, и это было предложено физиками Лизой Рэндалл и Раманом Сандрамом в 1999 году. Дополнительное пространственное измерение могло бы даже объяснить одна из величайших космических загадок: идентичность «темной материи», невидимого вещества, которое кажется в шесть раз тяжелее видимых звезд и галактик.