7Июл

Поворот движение по кривой самолета автомобиля велосипеда: Полет Самолета С Креном По Кругу Или Поворот По Кривой Автомобиля, Велосипеда 5 Букв

7 Июл 2023 alexxlab Комментировать

Полет Самолета С Креном По Кругу Или Поворот По Кривой Автомобиля, Велосипеда 5 Букв

Решение этого кроссворда состоит из 5 букв длиной и начинается с буквы В

Ниже вы найдете правильный ответ на Полет самолета с креном по кругу или поворот по кривой автомобиля, велосипеда 5 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Суббота, 6 Апреля 2019 Г.


ВИРАЖ

предыдущий следующий

ты знаешь ответ ?

ответ:

связанные кроссворды

  1. Вираж
    1. В вело- и мотоспорте: наклонный поворот трека 5 букв
    2. Раствор для окрашивания фотографических отпечатков 5 букв
    3. Движение автомобиля по кривой 5 букв
    4. Крутой поворот автомобиля 5 букв
    5. Место поворота 5 букв
    6. Наклонный поворот трека 5 букв

Вираж — понятие и значение

Рассмотрим что означает понятие и значение слова вираж (информация предоставлена intellect. icu).

Вираж это — 1. А) Поворот (обычно с креном), движение по кривой (автомобиля, мотоцикла, самолета и тому подобное). б) Резкое изменение направления полета (о птицах).
2. Место поворота, закругление на треке, беговой дорожке и тому подобное (обычно с наклоном внутрь). 2. Реактив, применяемый для окраски фотографий, диапозитивов и кинопленок в определенный цвет.

Вираж это — 1. Полет самолета с креном по кругу или поворот по кривой автомобиля, велосипеда. Войти в в. Крутые виражи. 2. В вело- и мотоспорте: наклонный поворот трека.

Вираж это — 1. Виража, ( французское virage — Поворот). 1. Место поворота на треке или снежной горе, где дорожка сделана наклонной (с портновское дело ). Крутой вира женский род 2. Поворот судна или аэроплана, уклонение их от пути по прямой линии ( морское дело , авиация).

ВИРАЖ

(в фотогр. деле). Особого рода раствор, в котор. погружают фотографич. пластинку прежде, чем её фиксировать.

ВИРАЖ

в фотографии жидкость для закрепления негативных изображений.

(1)

-а и -а, м.

1.

Поворот, движение по кривой (самолета, автомобиля, велосипеда и т. падеж ).

Крутой вира женский род Плоский вира женский род

.

Инженеры увидели большую птицу — она парила низко над поляной, делая странные резкие виражи. Ажаев, Далеко от Москвы.

2.

Участок дороги или спортивной дорожки с наклоном внутрь, приспособленный для криволинейного движения (автомобилей, велосипедов, мотоциклов и т. падеж ).

{Шубников} даже тренировался в езде по треку, думая взять приз на гонках, но слетел с виража, разбив колено. Федин, Первые радости.

{Франц. virage}

(2)

-а, м. Фото.

Химический раствор, в котором промывают отпечатанный снимок для придания ему определенной окраски.

{Франц. virage}


Часть речи

Имя существительное

Словоформы

виража, виражу, виражем, виражом, вираже, виражи, виражей, виражам, виражами, виражах

Синонимы wiki

фигура, повертка, раствор, поворот, поверток, реактив

Цифровое произношение

Вираж имеет soundex-В620, metaphone-«вираж», double-metaphone FRJ.

См. также

Понятие, виды. стадии Стартапов

… вложения , или оставить ее себе и получать . постянно от нее пассивный доход Гибкость старапа или виражи (pivot start-up ). Pivot (pivot , turn ) — это изменение направления стартапа с целью проверки … … методологией экономичного . стартапа Эрика Райса Как определить , когда нужно сделать вираж Проект не решает проблему пользователей Целевая аудитория , на которую вы нацелены , не … (Идея проекта, Start-up)

виражировать

ньютоновская механика — Почему наклоняющийся велосипед не падает?

Задавать вопрос

спросил

Изменено 5 лет, 3 месяца назад

Просмотрено 2к раз

$\begingroup$

Этот вопрос беспокоит меня уже некоторое время. Куда бы я ни посмотрел, все говорят о «фиктивных силах» и о том, как они, по-видимому, объясняют, что велосипед находится в равновесии. Однако, если мы просто посмотрим на простую диаграмму сил, мы увидим, что крутящие моменты вокруг определенных точек неуравновешены:

Если мы возьмем моменты вокруг, например, точки, где колесо касается земли, мы получим, что результирующий момент $amg\cos\theta$, где $a$ — некоторая длина, $m$ — масса объединенной системы водителя и велосипеда, а $\theta$ — угол между велосипедом и землей, действует так как заставить систему падать вниз в направлении центра.

Этот момент всегда будет «к центру» — независимо от положения велосипеда. Это означает, что он должен упасть. Так почему же нет? Ясно, что либо результирующего момента не должно быть, либо результирующий момент на протяжении одного круга, пройденного велосипедом, должен быть $0$, но здесь, очевидно, это не так. Что мне не хватает?

  • ньютоновская механика
  • динамика вращения
  • крутящий момент
  • центробежная сила
  • устойчивость
$\endgroup$

8

$\begingroup$

В инерционной раме крутящие моменты неуравновешены, и вращательный момент всадника вокруг точки на земле изменяется.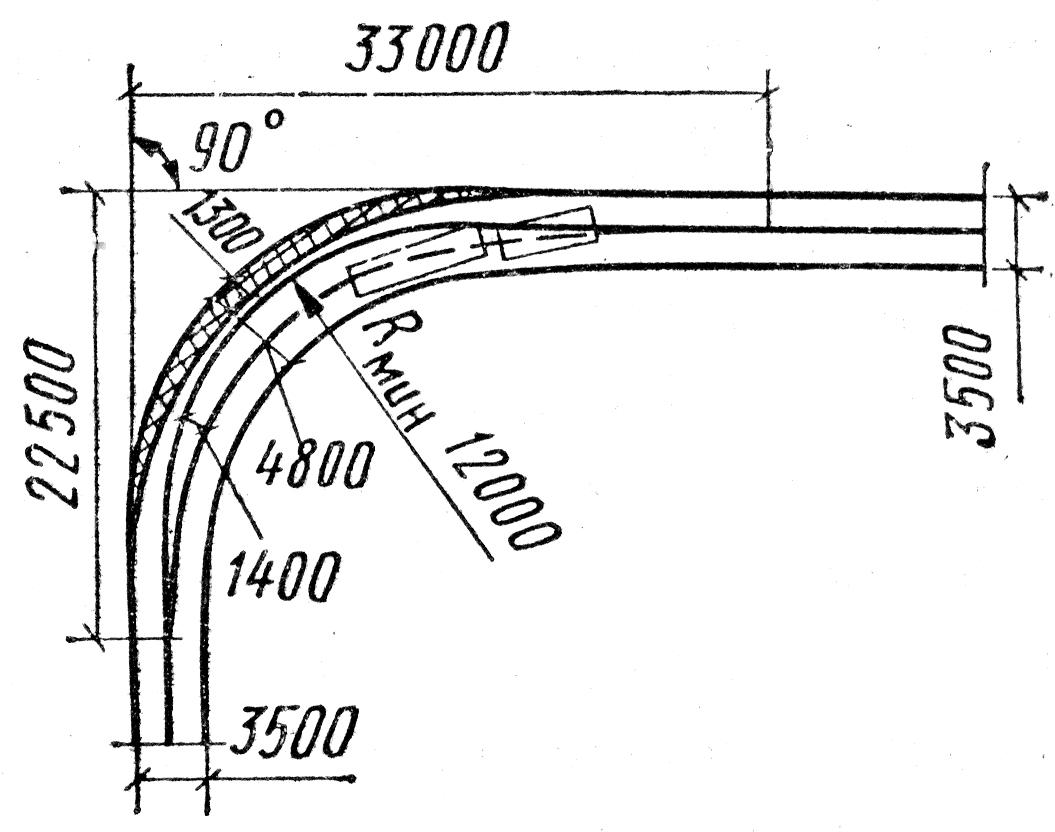

Просто это изменение не приводит к падению всадника.

Если вместо этого рассмотреть рамку, в которой всадник находится в покое, то в этой (ускоряющейся) рамке появятся фиктивные силы, противоположные ускорению.

Эти силы будут действовать через центр масс всадника и будут действовать в направлении, противоположном ускорению. Поскольку всадник ускоряется влево, справа должна действовать фиктивная сила отсчета. Это уравновешивает крутящие моменты относительно контакта шины.

$\endgroup$

2

$\begingroup$

Действительно, если бы велосипед ехал по прямой, он бы перевернулся. Это круговое движение, при котором всадник падает к центру круга, но постоянное изменение направления не позволяет велосипеду просто упасть на землю.

Представьте себе велодром, где проходят гонки на велосипедах. Когда всадник движется по кривой с креном, что произойдет, если бы кривая стала прямой, но все еще с креном? Что ж, гонщик начнет падать с берега не потому, что он толкает туда мотоцикл, а потому, что это происходит естественным образом. Его велосипед упадет из-за дисбаланса моментов, которые вы упомянули.

$\endgroup$

1

$\begingroup$

Просто потому, что, выполняя расчеты в системе отсчета самого велосипеда, вы делаете эти расчеты в ускоренной системе отсчета , и вам нужно учитывать ускорение, чтобы сбалансировать все.

Если вы производили расчеты в инерциальной системе отсчета, то в этой системе момент существует, но он уравновешивается моментом, создаваемым боковым ускорением через центр масс наружу от поворота.

$\endgroup$

$\begingroup$

Причиной того, что байкер не падает при наклоне в повороте, является центробежная сила, действующая на ЦМ байкера. Лучше всего это видно, когда байкер движется по кругу по кривой. Крутящий момент силы гравитации точно уравновешивается крутящим моментом центробежной силы, действующей на байкера. Описание вы найдете здесь.

Количественное описание: Поскольку вы, кажется, не согласны с тем, что центробежная сила объясняет проблему, я дам вам количественный вывод. 2}$$ Это показывает, что результирующий крутящий момент, действующий на байкера, действительно равен нулю для определенного угла наклона, что подтверждает опыт всех байкеров, движущихся по кривой.

$\endgroup$

8

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Ньютоновская механика — Почему трение заставляет автомобиль поворачиваться?

спросил

Изменено 9 месяцев назад

Просмотрено 13 тысяч раз

$\begingroup$ 92}{r}$, а направление ускорения – к радиусу окружности, по которой движется автомобиль. На диаграмме свободного тела автомобиля видно, что на него действуют только три силы: сила тяжести $(\vec{F_g})$, нормальная сила $(\vec{F_n})$ и трение $(\vec{ Ф_ф})$. Поскольку гравитация и нормальная сила отрицают друг друга, автомобиль не ускоряется в направлении $y$. Поскольку он находится в равномерном круговом движении, мы знаем, что он ускоряется в направлении $x$, и суммирование сил в этом направлении дает $$\vec{F_{net x}}=m\vec{a}=\vec{ F_f}$$ что означает, что центростремительное ускорение обусловлено силой трения.

Мне трудно понять, почему это интуитивно понятно. Я читал ответы других людей на этот вопрос, но не нашел ничего удовлетворительного. В частности, многие люди говорят о том, что колеса «толкают тротуар влево или вправо», и это заставляет тротуар воздействовать на колеса автомобиля в соответствии с третьим законом Ньютона, но для меня это не имеет смысла.

Другими словами, я не понимаю, почему трение должно быть направлено внутрь, к центру круга, вокруг которого вращается человек. Я ожидаю, что, поскольку колеса повернуты, это трение будет направлено в направлении, противоположном направлению движения автомобиля, чтобы автомобиль не продолжал двигаться вперед и не скользил по дороге.

  • ньютоновская механика
  • силы
  • трение
  • диаграмма свободного тела
$\endgroup$

1

$\begingroup$

Мне было весело пытаться сделать это как можно более интуитивным. Я надеюсь, что мне это удалось, не причинив большой несправедливости физике ситуации.

Когда автомобиль движется прямо, плоскость, в которой вращаются колеса, совпадает с направлением движения. Другими словами, ось вращения перпендикулярна вектору импульса $\vec{p}=m\vec{v}$ автомобиля. Таким образом, трение просто затрудняет движение автомобиля, что является одной из причин, по которой вам нужно нажать на педаль газа, чтобы поддерживать постоянную скорость. В то же время именно трение позволяет вам поддерживать постоянную скорость, потому что вращающиеся шины как бы схватиться за землю , что является интуитивной картиной трения. Шины цепляются за землю и тянут/толкают ее назад под себя, как если бы вы тащили себя по полу (если бы у него были ручки, за которые можно было бы ухватиться). Эти хватающие и тянущие/толкающие силы — вот что поддерживает вас.

Все меняется, когда крутятся колеса. Плоскость, в которой они теперь вращаются, находится под углом к ​​направлению движения. В качестве альтернативы, но эквивалентно, мы могли бы сказать, что ось вращения теперь образует угол с вектором импульса автомобиля. Чтобы увидеть, как трение затем заставляет машину поворачиваться, подумайте еще раз о том, как колеса цепляются за землю. Тот факт, что теперь они образуют угол с направлением движения, означает, что сила, которую прилагают шины, также находится под углом к ​​направлению движения, или, что то же самое, вектор импульса. 91$ Математически: $$\vec{F}=\frac{d\vec{p}}{dt}$$

$\endgroup$

2

$\begingroup$

Ключевым моментом ИМО является то, что «эффективное трение» свободно вращающегося колеса сильно различается в разных направлениях. При движении вместе с колесом эффективное трение мало, потому что колесо может вращаться. При движении перпендикулярно колесу эффективное трение — это просто высокое трение между поверхностью колеса и землей.

Если колесо параллельно направлению движения, то оно оказывает небольшую силу, замедляющую автомобиль. Если он перпендикулярен автомобилю, то он оказывает гораздо большую силу, замедляя автомобиль.

Чтобы увидеть, что происходит, когда мы поворачиваем колеса по диагонали, давайте разложим скорость автомобиля на компоненты, параллельные и перпендикулярные колесу. Оба этих компонента будут указывать по диагонали вперед. Это означает, что их соответствующие силы трения направлены по диагонали назад.

из-за более высокого эффективного трения составляющая силы трения, перпендикулярная колесу, будет намного больше, чем составляющая, параллельная колесу. Так что давайте только рассматривать это один с этого момента. если передняя часть колеса направлена ​​вправо, то перпендикулярная сила трения будет направлена ​​назад и вправо.

Разлагая эту силу обратно на машину, мы видим силу, направленную назад, и силу, направленную вправо.

Если бы автомобиль был симметричным в четырех направлениях и все колеса вращались бы в одном направлении, то автомобиль просто начал бы двигаться по диагонали, но колеса автомобиля этого не делают. поворачиваются только передние колеса, поэтому передняя часть автомобиля толкается вправо, заставляя машину поворачивать вправо.

$\endgroup$

$\begingroup$

Если мы хотим удержать тело на круговой орбите, необходима центральная сила. Если это достаточно интуитивно понятно, то когда вы поворачиваете руль, вы эффективно меняете направление движущей силы (если мы движемся с постоянной скоростью, эта сила все еще существует, хотя она уравновешивается точно с полными силами трения). не изменить направление скорости мгновенно. если вы сделаете только одно изменение угла движущей силы, потребуется конечное количество времени, чтобы приспособить транспортное средство к новому углу. Таким образом, именно Инерция дает это кажущееся скольжение. Круговая орбита немного отличается, вы продолжаете изменять направление движущей силы, теперь, поскольку инерция заставляет транспортное средство скользить все время, пока действует сила трения. Но максимальная сила трения ограничена mu * R , R = mg , Если центральная сила, необходимая для нашей предполагаемой орбиты, меньше, чем my * R, тогда транспортное средство поддерживает минимальное скольжение, но если оно недостаточно, проскальзывание и поворот происходят последовательно до тех пор, пока мы достигнем большей орбиты с более высоким радиусом кривизны, что сделает центральную силу меньше (поскольку она равна mv ^ 2/r), чтобы она могла поддерживаться mu * R ( mu — коэффициент трения) В качестве альтернативы V можно было бы сделать меньше, чтобы сила трения могла поддерживать необходимую центральную силу. Главное, нет двух сил центробежной и центростремительной, это только сбивает с толку. Дело в той центральной силе, которая нужна для конкретной орбиты и скорости. Это должно исходить из каких-то внешних средств.

P.S. Далее уточните внезапное изменение направления движения автомобиля, движущегося с постоянной скоростью. Как только мы его повернем, вы сможете определить скорость в двух направлениях. один вдоль нового направления и перпендикулярно этому направлению. Теперь перпендикулярная составляющая будет толкать транспортное средство наружу с силой трения в направлении, противоположном скольжению. Из-за этого «перпендикулярная скорость» уменьшится. Однако, если это остается прежним, постоянная скорость транспортного средства в новом направлении не увеличивается обратно до v, потому что движущей силы едва хватает для поддержания постоянной скорости, т. Е. Нет ускорения. Из-за поворота теряется кинетическая энергия. Ключевым моментом здесь является инерция.

$\endgroup$

$\begingroup$

Вот ответ, который вы искали, он интуитивно понятен и полностью удовлетворит ваше любопытство.

Начните с осмотра одного колеса машины, проходящей поворот. Он движется по криволинейной траектории и испытывает боковую силу трения. Если снять колесо с машины и покатать ее, она будет катиться только прямо. Чтобы заставить его изменить направление и двигаться по криволинейной траектории во время вращения, вы должны повернуть его вокруг вертикальной оси, применив крутящий момент вертикальной оси. Обратите внимание, что при вращении колеса вокруг вертикальной оси во время его вращения на него будет действовать боковая сила. Здесь у вас есть колесо, прилагающее силу к тротуару, и, согласно третьему закону Ньютона, тротуар прилагает силу к колесу.

Теперь у нас есть одно колесо, которое движется по криволинейной траектории и испытывает боковую силу. Вот неинтуитивная часть, но вы увидите, что это правда через некоторое время. Если бы все четыре колеса движущегося на повороте автомобиля испытывали постоянные крутящие моменты по вертикальной оси, все они двигались бы по криволинейной траектории и испытывали бы боковые силы.