Необслуживаемый аккумулятор, как вас обслужить?

Советы профессионалов Аккумуляторного дома в Санкт-Петербурге

Посмотреть подробное видео на нашем канале

Очевидно, что лишние хлопоты с автомобилем никому не интересны. По этой причине многие автомобилисты, в том числе профессионалы, ставят так называемые кислотные необслуживаемые аккумуляторы действуя по принципу «поставил и забыл».
В этой статье мы расскажем о том, какие плюсы и минусы имеет кислотный необслуживаемый аккумулятор, насколько он действительно необслуживаемый и как его правильно эксплуатировать.
Для начала давайте определим, что такое кислотный необслуживаемый аккумулятор и как он выглядит внешне.
Сразу обратите внимание на наличие пробок для доступа к электролиту. Если пробок нет, то это необслуживаемый аккумулятор.
Но это признак необязательный. Забегая вперёд, скажем, что на хороших аккумуляторах пробки есть.

Как понять, обслуживаемый перед вами аккумулятор или нет

Иногда на батарее может быть написано по-английски maintenance-free.

Иногда может быть указана технология «кальций-кальций» или Ca-Ca. Не волнуйтесь, далеко в электрохимию не полезем, достаточно запомнить название технологии «кальций-кальций».

Почему же такое устройство считается необслуживаемым, и в чём это отсутствие обслуживания проявляется?

Как следует из названия, электролит в такой батарее кислотный, в жидком состоянии. А жидкости имеют свойство испаряться. Точнее, из электролита испаряется вода.

Современные технологии позволяют создавать аккумуляторы, у которых это испарение минимально.

Поэтому долива дистиллированной воды такие батареи не требуют в течение всего срока службы.

Как вы понимаете, именно по этой причине на таких аккумуляторах может не быть пробок.

Вы будете удивлены, но всё отсутствие обслуживания сводится исключительно к тому, что владельцу не нужно контролировать уровень электролита. Тем не менее, это серьёзный плюс кислотного необслуживаемого аккумулятора.

Следующий плюс, который напрямую связан именно с технологией «кальций-кальций» — это низкий саморазряд. Что это значит для владельца?

За достаточно большой промежуток времени, например, за месяц, пока вы в отпуске и автомобилем не пользуетесь, аккумулятор практически не потеряет заряд. Если, конечно, вы его отключили — сняли с него клеммы. Тогда, вернувшись с курорта, вы сядете в машину, повернёте ключ зажигания и спокойно поедете.

Плюсы необслуживаемых аккумуляторов

Ещё один положительный момент у таких батарей – это повышенный пусковой ток. На практике это означает, что аккумулятор меньшей ёмкости сможет запустить более тяжёлый двигатель.

Итак, плюсы:
— нет никакой работы с электролитом;

— низкий саморазряд;

— повышенный пусковой ток;

А сейчас поговорим о недостатках, которые имеет кислотный необслуживаемый аккумулятор.

Минусы необслуживаемых аккумуляторов

ПЕРВЫЙ минус – эти батареи боятся глубоких разрядов.

Чем это грозит владельцу? Когда двигатель заводится не с первого раза, а приходится делать несколько попыток, вполне возможен случай, что при очередной попытке энергии аккумулятора просто не хватит на запуск. Или, когда бортовая сеть потребляет энергии больше, чем успевает произвести генератор. Такой вариант тоже может привести к глубокому разряду. А глубокий разряд – это практически выход батареи из строя, поскольку выводить из состояния глубокого разряда аккумулятор, выполненный по технологии «кальций-кальций» (вы уже запомнили это название?) очень непросто.

А теперь внимание! Сейчас для многих будет удивительное открытие: необслуживаемые аккумуляторы ТРЕБУЮТ зарядки! Да, да, это не ошибка! Необслуживаемые аккумуляторы ТРЕБУЮТ зарядки.

Если вы хотите, чтобы ваша батарея проработала долго, вам придётся РЕГУЛЯРНО контролировать степень заряда батареи, а при наличии пробок и плотность электролита.

А два раза в год – перед зимним сезоном и после него – производить штатный (нормальный) заряд батареи. Иначе аккумулятор может работать с систематическим недозарядом, что приведет к выходу его из строя.

Мы говорили о систематическом недозаряде и глубоком разряде. Подробный рассказ об этих неприятностях в нашем учебном ролике «Как продлить «жизнь» аккумулятора». Кроме того, часть информации вы можете почерпнуть из другого нашего учебного ролика «Менять или заряжать?». Текстовые варианты обоих этих роликов представлены в разделе «Блог», в материалах с теми же названиями.

Чуть ниже мы дадим чёткую инструкцию, как правильно заряжать аккумулятор «кальций-кальций».

Второй минус аккумулятора технологии «кальций-кальций»: его заряд очень непростой!

Оговоримся сразу: пока аккумулятор регулярно и полностью подзаряжается, никаких проблем нет. Но, как только состояние батареи приближается к критическому (к состоянию глубокого разряда), так начинаются те самые сложности.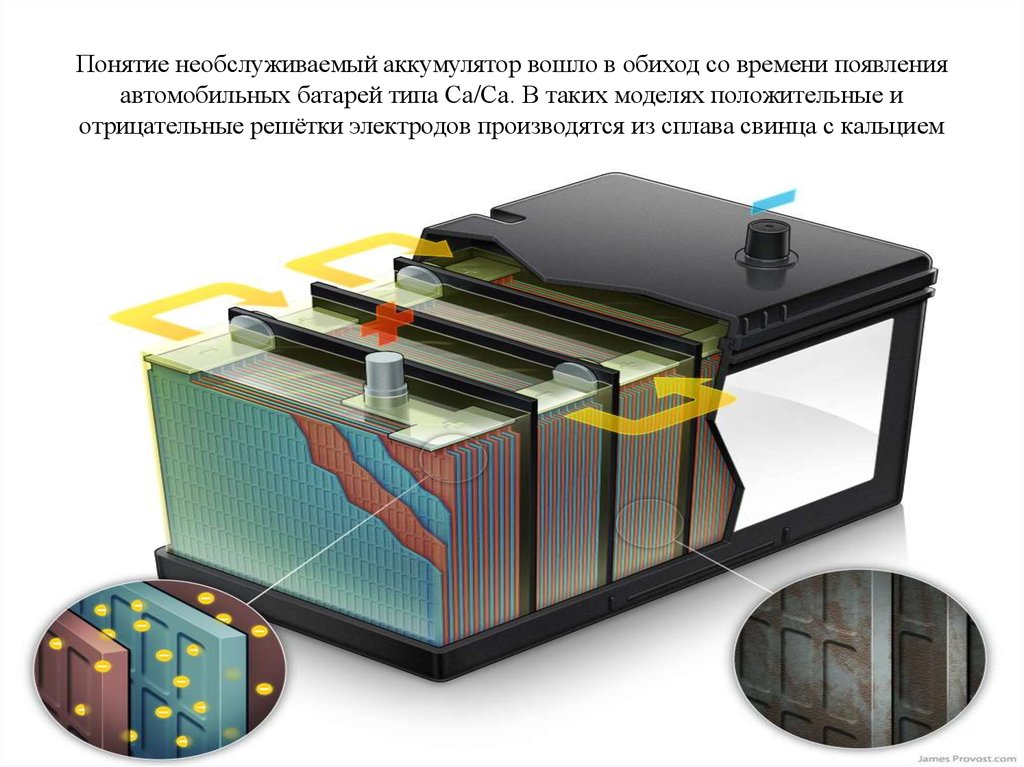 А вот обнаружить глубокий разряд заранее никак не получится – только по факту. То есть машина просто не завелась. Не слишком бодро звучит, правда?

Так вот о сложностях.
Начнем с того, что конечное напряжение заряда для этого типа батарей должно быть в пределах от 15,0V до 16,5V. Точное значение напряжения определяется лигирующими компонентами в химическом составе аккумулятора и температурой заряда.

Штатный генератор далеко не всегда сможет выдать такое напряжение – обычно его значение ограничено величиной 14,4V, а чаще и более низкой.

А это практически гарантированный недозаряд!

Да, мы уже слышим, как наиболее догадливые говорят: «Так нужно просто поднять напряжение генератора покрутив настройку реле!» Даже если это можно сделать, то панацеей такая регулировка не станет. И дальше вы поймете, почему.

Так что пока просто запомните, что вывести батарею ГЕНЕРАТОРОМ из критического состояния невозможно.

Остаётся вариант подзаряда зарядным устройством.

Зарядное устройство не просто должно выдавать напряжение выше 15-ти Вольт, оно должно уметь контролировать ток заряда, постепенно его уменьшая. Скажем прямо – такие интеллектуальные устройства – большая редкость. Так что если автоматика вашего зарядного устройства не умеет этого делать, то придется крутить настройки руками. Вот только учтите, что зарядка аккумулятора — это не пять минут, и даже не час.

МИНИМАЛЬНОЕ время вывода батареи из критического состояния — СУТКИ!

А при особо тяжёлых случаях до трёх суток! Вы готовы дежурить у аккумулятора трое суток, каждые 2-4 часа проверяя параметры заряда? Ведь процесс заряда прерывать нельзя! Теперь вы понимаете, что никакая регулировка напряжения генератора ничего не решит?

Далее мы приводим примерный график заряда аккумулятора «кальций-кальций». Точные значения величин напряжения указать невозможно, поскольку это зависит от лигирующих добавок конкретного производителя. Кроме того, скорость процесса будет зависеть от температуры. Мы приводим значения напряжений для температуры 20 градусов Цельсия.

Для простоты расчёта тока и большей наглядности будем считать, что ёмкость аккумулятора 100 Ампер-часов.

Итак, первая ступень.

Ставим ограничение конечного напряжения на значение 14,6V – 14,8V, задаём ток 7% от ёмкости. Для ёмкости 100 Ампер-часов это 7 Ампер.

Если зарядное устройство программируемое, то оно само переключит заряд на следующую ступень. Если всё делается руками, то нужно следить за вольтметром, и когда он покажет напряжение 14,6V – 14,8V, переключить зарядное устройство на вторую ступень.

Обратите внимание, что время в данном случае вторично и зависит только от степени разряда батареи. То есть единственный параметр, по которому мы можем судить об окончании первой ступени заряда, — это достижение аккумулятором заданного конечного напряжения.

Тот же принцип будет относиться и ко второй ступени.

Вторая ступень

Устанавливаем конечное напряжение 15,0V – 15,2V, ток 3% от номинала. В нашем случае 3 Ампера. И так же не обращаем внимание на время, ждём достижения указанного напряжения, если всё делаем сами. Или доверяем программе зарядного устройства.

Третья ступень

Устанавливаем конечное напряжение 15,2V – 16,0V, ток 1% от номинала. В нашем случае 1 Ампер.

А вот третья ступень должна длиться не менее 10 часов.

После этого выжидаем сутки.

Теперь нужно замерить нагрузочной вилкой напряжение без нагрузки и под нагрузкой. А для аккумуляторов с пробками ещё и измерить плотность электролита.

Для полностью заряженного аккумулятора напряжение без нагрузки должно быть не менее чем 12,8V, а под нагрузкой – не менее 10,8V.

Плотность электролита 1,27-1,28 г/см³.

Обращаем ваше внимание, что такой трёхступенчатый заряд для аккумуляторов «кальций-кальций» используется и для нормального заряда, и для вывода из глубокого разряда. Единственное различие в том, что нормальный заряд займет 10-14 часов, а вот вывод из глубокого разряда, как мы говорили, может длиться до трёх суток.

И, конечно, первым попавшимся зарядным устройством этого не сделать.

Ну, как? Вы всё ещё верите в необслуживаемость аккумулятора?

Итак, главная рекомендация для аккумулятора «кальций-кальций»:

РЕГУЛЯРНО КОНТРОЛИРУЙТЕ ЗАРЯД, НЕ ДОПУСКАЙТЕ ГЛУБОКОГО РАЗРЯДА!

Ещё раз напомним, что для более полной информации посмотрите наши видео «Как продлить «жизнь» аккумулятора» и «Менять или заряжать?».

С вами были специалисты компании Аккумуляторный дом.

Следите за нашими новыми выпусками!

Поделиться

К списку статей

Фронт-терминальный герметичный необслуживаемый аккумулятор Tesla Power 12VDC 180Ач

Свинцово-кислотный герметичный необслуживаемый аккумулятор Tesla Power с регулируемым клапаном VRLA (Valve-Regulated Lead-Acid) с внутренней рекомбинацией газа и абсорбированным электролитом (технология AGM Absorbent Glass Mat). Фронтальное исполнение.

Батареи Tesla Power предназначены для установки в 19, 23 дюймовые шкафы и стойки, также используются в других случаях, когда необходимо компактное размещение батарей.

Фронтальное расположение клемм облегчает установку и сокращает время на обслуживание и замену батарей. Хорошие характеристики при небольших токах разряда делают эти батареи лучшим выбором для телекоммуникационных систем и других ответственных нагрузок, рассчитанных на длительное время автономии.

Применение

— Системы электросвязи;
— Источники бесперебойного питания ( ИБП, UPS) переменного и постоянного тока;
— Системы аварийного питания заводов и подстанций;
— Солнечные и ветряные источники энергии;
— Производство, транспорт и распределение электроэнергии;
— Устройства автоматики на железных дорогах;
— Складское оборудование;
— Аварийное освещение;
— Медицинское оборудование.

Аккумулятор не требует обслуживания в течение всего срока службы и обеспечивает высокую безопасность во время эксплуатации. Герметичная конструкция батареи позволяет транспортировать ее любым видом транспорта.

Конструкция аккумулятора. Многослойная технология, ячеистая конструкция батареи, специальный клей, обеспечивает компактность и защиту от вибраций и ударов.

Материал корпуса. Корпус и крышка батареи изготовлены из негорючего ударопрочного пластика ABS.

Защитный клапан. Клапан выполнен пожаровзрывобезопасными.

Сепаратор. Сепаратор между положительными и отрицательными пластинами выполнен из тонкого стекловолокна. Обеспечивает низкое сопротивление при разрядах большим током.

Пластины батареи. Пластины батареи прямоугольной формы. Благодаря применению специальной структуре и особого сплава, увеличивается плотность энергии на единицу массы и объема, а также повышается срок службы батареи.

Электролит. Электролит высокой степени очистки содержит добавки, улучшающие разрядные характеристики.

Соединение пластин в блоки. Специальная форма сепаратора позволяет плотно компоновать пластины. Эластичность материала обеспечивает равномерный контакт с пластинам, тем самым обеспечивается однородность электрохимических параметров по всей площади.

Борны. Встроенные медные выводы имеют малое сопротивление и выдерживают высокий ток.

Защита от короткого замыкания. Конструкция гнезд пластин обеспечивает защиту от короткого замыкания в случае изгиба или деформации пластин, в случае горизонтального расположения батареи.

 

Уважаемые покупатели.
Обращаем Ваше внимание, что размещенная на данном сайте справочная информация о товарах не является офертой, наличие и стоимость оборудования необходимо уточнить у менеджеров ООО «LIDER TEAM», которые с удовольствием помогут Вам в выборе оборудования и оформлении на него заказа.

Производитель оставляет за собой право изменять внешний вид, технические характеристики и комплектацию без уведомления.

«Многоцелевой подход к оптимальному хранению батарей в присутствии», Реза Камьяр и Мэтью Монниг Пит

• < Предыдущий
• Далее >
•  

 

Ключ

33648

Конференция Год

2016

Ключевые слова

Хранение аккумуляторов, зарядка по требованию, многозадачность 12 Abstract

В этой статье мы предлагаем основу оптимизации для оптимального накопления энергии в виде аккумуляторов для бытовых потребителей. Наша цель — определить ценность аккумуляторных батарей для тех клиентов, чьи счета за электроэнергию состоят из платы за время использования (долл. США/кВтч, с разными ставками в пиковые и непиковые часы) и платы за потребление (долл. США/кВт). , пропорционально максимальной норме потребления за месяц). Клиенты могут иметь доступ к местному источнику электроэнергии в виде солнечной фотогальванической установки (PV). Чтобы количественно оценить выгоды от аккумуляторной батареи, мы ставим задачу оптимизации батареи, которая минимизирует ежемесячный счет за электроэнергию. pd supk-on q(k), где poff, pon,  pd — цены в непиковый период, пиковый период и спрос, а q(k) — мощность, поставляемая коммунальной компанией потребителю. Мы считаем, что эта мощность используется согласно формуле q(k) = qb(k) + qa(k) — qsolar(k), где qa — мощность, потребляемая электроприборами, qsolar — мощность, обеспечиваемая фотоэлектрическими солнечными батареями, а qb — мощность, отдаваемая или отбираемая от батареи. Мы предполагаем, что скорость энергии, запасенной в батарее, пропорциональна qb, а запасенная энергия ограничена емкостью батареи (кВтч). Кроме того, мы учитываем деградацию батареи, моделируя емкость батареи в зависимости от количества циклов зарядки/разрядки и глубины разрядки. Из-за наличия платы за спрос (supk q(k)), целевая функция нашей задачи оптимизации батареи не является разделимой во времени — свойство (временная разделимость), достаточное для того, чтобы алгоритм динамического программирования сходился к оптимальному решению. . Мы устанавливаем доказуемо сходящийся алгоритм для задачи неразделимой оптимизации в следующих двух шагах. Сначала заменим supk q(k) в целевой функции, используя следующую аппроксимацию Предположение о q(k) = q(k) для некоторого большого р. Затем мы строим многокритериальную задачу (класс задач оптимизации, включающую как минимум две целевые функции, которые должны быть минимизированы одновременно), определяемую параметризованным набором динамических программ, выраженных через функции с разделением во времени J1(q) = ˆ ˆ k q(k) J2(q) = −kâˆon q(k)p Каждая из этих параметризованных динамических программ может быть решена с использованием стандартных алгоритмов динамического программирования. Набор решений этих параметризованных задач образует фронт Парето — набор, который гарантированно содержит решение исходной задачи оптимизации батареи как p †’ ˆž. Мы применяем наш алгоритм к нескольким сценариям, описываемым диапазоном размеров батарей, уровнями солнечной генерации и нагрузками на бытовые приборы, чтобы количественно оценить экономию от батарей для широкого круга бытовых потребителей. Предлагаемый подход потенциально может быть использован для: 1) моделирования реакции потребителей на изменение цен на электроэнергию; 2) Количественно оценить преимущества хранения энергии для коммунальных предприятий.

Скачать

ЗАГРУЗКИ

С 12 декабря 2016 г.

МОНЕТЫ

 

Симметрия | Бесплатный полнотекстовый | Неразделимое линейное каноническое вейвлет-преобразование

1. Введение

Происхождение многомерного линейного канонического преобразования (LCT) восходит к началу 1970-х годов с фундаментальной работой Мошинского и Кена [1] в квантовой механике для изучения линейные отображения фазового пространства. Вскоре после своего появления в квантовой механике линейное каноническое преобразование изучалось исключительно как в теории, так и в приложениях [2,3]. Теория многомерного несепарабельного LCT, включающего общую 2n × 2n вещественную симплектическую матрицу M = (A, B: C, D) с n (2n + 1) независимыми параметрами, предлагает канонический формализм для представления нескольких физических системы в ясной и проницательной форме. Для любого f∈L2(Rn) несепарабельный LCT относительно вещественной симплектической матрицы M задается формулой [4,5]

Важность произвольных вещественных симплектических матриц, участвующих в уравнении (1), заключается в том, что правильный выбор матрицы может привить ощущение вращения и сдвига как по оси времени, так и по оси частоты, что приводит к эффективному представление чирп-подобных сигналов, которые широко распространены как в природе, так и в искусственных системах. Благодаря дополнительным степеням свободы несепарабельная ЛВТ успешно применяется в разнообразных задачах, возникающих в различных областях науки и техники, таких как гармонический анализ, гильбертовы пространства с воспроизводящим ядром, оптические системы, квантовая механика, дискретизация, обработка изображений, и так далее [6,7].

Несомненно, вейвлет-преобразования очаровали научное, инженерное и исследовательское сообщества как своей универсальной применимостью, так и ясной математической структурой [8,9]. В последние годы классическое вейвлет-преобразование было расширено и использовано в различных областях. Наиболее быстрыми из них являются дробное вейвлет-преобразование [10], линейное каноническое вейвлет-преобразование [11,12], специальное аффинное вейвлет-преобразование [13,14], кватернионное линейное каноническое вейвлет-преобразование [15] и квадратично-фазовое вейвлет-преобразование [16]. ]. К сожалению, все эти преобразования хорошо работают только при представлении точечных сингулярностей и не подходят для обработки распределенных сингулярностей, таких как кривые или ребра в многомерных сигналах [17,18,19].,20]. Интуитивная причина этой неадекватности заключается в том, что вейвлеты являются изотропными объектами, генерируемыми путем изотропного расширения материнского вейвлета, и поэтому они игнорируют геометрические свойства анализируемых структур. Таким образом, традиционный вейвлет-подход не подходит при работе с многомерными сигналами, где основной интерес заключается в эффективном захвате геометрических особенностей, таких как края и углы, возникающие из-за пространственной окклюзии между различными объектами. Таким образом, ключевая проблема в многомерном анализе сигналов состоит в том, чтобы извлечь и охарактеризовать соответствующую геометрическую информацию о появлении кривых и границ в сигналах. Впоследствии был предложен многомерный вариант стандартного вейвлет-преобразования, который служит мощным инструментом для представления непереходных многомерных сигналов в частотно-временной области. Математически многомерное вейвлет-преобразование любого f∈L2(Rn) определяется формулой [21]

где a называется параметром масштабирования, который управляет степенью сжатия или масштабирования, а b — параметром перевода, определяющим временную позицию вейвлета. Многомерное вейвлет-преобразование в уравнении (2) нашло множество применений в различных областях науки и техники, в частности, в обработке видеоизображений, медицинской визуализации, задачах сингулярного обнаружения, гидродинамике, распознавании форм и т. д. [21,22]. . В контексте многомерной теории вейвлетов свойство симметрии вейвлетов часто желательно в практических приложениях, и как таковые вейвлеты могут выявлять различные закономерности и особенности сильно нестационарных сигналов, таких как броуновские движения, закономерности на поверхности воды, фрактальные свойства поля скоростей, вычисление размерностей Реньи, показателей Херста и Гёльдера. Некоторые известные примеры симметричных вейвлетов включают биортогональные вейвлеты, вейвлеты квинконса и каринальные B-сплайны.

Принимая во внимание глубокие характеристики многомерного вейвлет-преобразования и больше степеней свободы неразделимых линейных канонических преобразований, мы глубоко мотивированы переплести эти интегральные преобразования в новое интегральное преобразование, придуманное как неразделимое линейное каноническое преобразование. вейвлет-преобразование. Новое интегральное преобразование может эффективно локализовать любой непереходный сигнал в частотно-временной плоскости с большим количеством степеней свободы. Со значительными изменениями существующего многомерного вейвлет-преобразования в уравнении (2) мы предлагаем неразделимое линейное каноническое вейвлет-преобразование любого f∈L2(Rn) относительно свободной симплектической матрицы M=A,B:C,D как

где Λа=(аа…а)Т. Помимо изучения всех фундаментальных свойств нового вейвлет-преобразования, мы выводим некоторые известные теоремы, в том числе теорему Рэлея, формулу обращения и теорему о диапазоне. В дальнейшем мы также сформулируем несколько неравенств неопределенностей, таких как неравенства Гейзенберга, логарифмические неравенства и неравенства типа Назорава для неразделимого линейного канонического вейвлет-преобразования в уравнении (3).

Остальная часть статьи структурирована следующим образом: Раздел 2 посвящен предварительным аспектам исследования и формулировке неразделимого линейного канонического вейвлет-преобразования. Раздел 3 посвящен формулировке нескольких вариантов принципов неопределенности, таких как неравенства Гейзенберга, логарифмические неравенства и неравенства типа Назорава, для предлагаемого преобразования. Наконец, в разделе 4 делается вывод.

2. Неразделимое линейное каноническое вейвлет-преобразование в L2(Rn)

В этом разделе мы сначала даем обзор неразделимого линейного канонического преобразования. Затем мы вводим понятие несепарабельного линейного канонического вейвлет-преобразования в L2(Rn), за которым следуют некоторые фундаментальные свойства предлагаемого преобразования, включая соотношение ортогональности, соотношение сохранения энергии, теорему о диапазонах и формулу обращения.

2.1. Неразделимое линейное каноническое преобразование

Для типографского удобства мы будем обозначать вещественную матрицу 2n×2n

как M = A, B: C, D, где A, B, C и D — подматрицы размера n × n с действительными элементами. Кроме того, матрица M=A,B:C,D называется свободной симплектической, если MTJM=J и detB≠0, где J=0,In:−In,0, а In обозначает n-мерную единичную матрицу. Кроме того, подматрицы, соответствующие свободной симплектической матрице M = (A, B: C, D), удовлетворяют

или эквивалентно

Транспонированные и обратные, соответствующие свободной симплектической матрице M=A,B:C,D, задаются как MT=AT,CT:BT,DT и M−1=DT,−BT:−CT,AT соответственно. Более того, у нас есть

Типичный пример свободной симплектической матрицы 4 × 4 приведен ниже.

Аддитивное свойство неразделимого LCT (уравнение (7)) очень важно для его понимания и применения и определяется выражением

Формулы Планшераля и обращения, соответствующие уравнению (7), имеют вид

соответственно, где M−1=DT,−BT:−CT,AT. Кроме того, ядро ​​в уравнении (8) удовлетворяет следующим свойствам:

(i)

KM−1(w,t)=KM(t,w)¯,

(ii)

∫RnKM(t,w)KM−1(t,z)dt=δ(z−w),

(iii)

∫RnKM(t,w)KM −1(z,w)dw=δ(z−t),

(iv)

∫RnKM(t,w)KN(t,z)dt=KMN(w,z).

Неразделимое линейное каноническое преобразование (уравнение (7)) охватывает несколько хорошо известных интегральных преобразований, включая преобразование Фурье (FT), дробное преобразование Фурье (FrFT), линейное каноническое преобразование (LCT) и преобразование Френеля. трансформы (FrT) [4]. В таблице 1 показаны некоторые частные случаи несепарабельного линейного канонического преобразования.

2.2. Неразделимое линейное каноническое вейвлет-преобразование

Вейвлеты действуют как оконные функции, радиус которых увеличивается во времени (уменьшается по частоте) при разрешении низкочастотного содержимого и уменьшается во времени (увеличивается по частоте) при разрешении высокочастотного содержимого не- переходный сигнал. Математически семейство вейвлетов ψa,b с двойным индексом генерируется ограничением параметра масштабирования a, принадлежащего R+, и параметра трансляции b, принадлежащего Rn, как [8]:

Параметр масштабирования a измеряет степень сжатия или масштабирования, тогда как параметр преобразования b определяет местоположение вейвлета. С большими модификациями семейства (уравнение (4)) мы определяем новое семейство функций ψa,bM(t) относительно свободной симплектической матрицы M=A,B:C,D как:

где

где Λа=(аа…а)Т. Сформулировав семейство анализирующих функций, мы теперь готовы ввести определение несепарабельного линейного канонического вейвлет-преобразования в L2(Rn).

Определение 2 позволяет сделать следующие комментарии:

(i) Неразделимое линейное каноническое вейвлет-преобразование может быть записано в форме скалярного произведения как

где ψa,bM(t) определяется уравнением (12).

(ii) Стоит отметить, что предлагаемое преобразование в уравнении (7) охватывает несколько существующих интегральных преобразований, таких как классическое вейвлет-преобразование, дробное вейвлет-преобразование, линейное каноническое вейвлет-преобразование и т. д. [8,9]. Соответствующие вейвлет-преобразования можно получить, выбрав подходящую симплектическую матрицу M=(A,B:C,D).

Теперь мы представляем пример для наглядной иллюстрации предлагаемого неразделимого линейного канонического вейвлет-преобразования в уравнении (14).

Неразделимые линейные канонические вейвлет-преобразования, показанные в уравнении (26) для f, соответствующие Λ=(1,1), представлены на рис. 4, рис. 5 и рис. 6.

Далее мы выведем фундаментальное соотношение между неразделимое линейное каноническое вейвлет-преобразование (уравнение (7)) и неразделимое линейное каноническое преобразование (уравнение (1)). С помощью этой формулы изучим основные свойства предлагаемого преобразования.

2.3. Основные свойства неразделимого линейного канонического вейвлет-преобразования

В этом подразделе мы изучим некоторые математические свойства предложенного неразделимого линейного канонического вейвлет-преобразования (уравнение (7)), включая теорему Рэлея, формулу обращения и диапазон теорема. В этом направлении у нас есть следующая теорема, которая собирает некоторые из основных свойств предложенного преобразования.

Далее определим условие допустимости функции ψ∈L2(Rn).

Теперь мы можем вывести соотношение ортогональности для предлагаемого преобразования, определенного в уравнении (7). Как следствие соотношения ортогональности, мы покажем, что несепарабельное вейвлет-преобразование является изометрией пространства квадратично-интегрируемых функций L2(Rn) в пространство преобразований L2(Rn×R+).

В нашей следующей теореме мы показываем, что несепарабельное линейное каноническое вейвлет-преобразование WψMf(a,b) любой функции f∈L2(Rn) обратимо в том смысле, что f может быть легко восстановлена ​​из преобразованной области L2( Rn×R+).

Наконец, мы исследуем характеристику диапазона для предлагаемого преобразования (уравнение (7)). Как следствие теоремы о диапазоне, мы покажем, что диапазон неразделимого линейного канонического вейвлета преобразуется; т. е. WψM(L2(Rn)) — гильбертово пространство с воспроизводящим ядром.

3. Принципы неопределенности для неразделимого линейного канонического вейвлет-преобразования

Принцип неопределенности лежит в основе гармонического анализа, который утверждает, что «положение и скорость частицы не могут быть точно определены одновременно» [23]. Версия этого принципа для гармонического анализа утверждает, что «нетривиальная функция не может быть должным образом локализована как во временной, так и в частотной областях одновременно» [24]. Это стандартное неравенство широко изучалось во многих областях и аспектах [25,26,27]. Принимая во внимание тот факт, что принципы теории неопределенности для неразделимого линейного канонического вейвлет-преобразования еще предстоит изучить исключительно; поэтому как теоретически, так и практически интересно разработать некоторые новые принципы неопределенности, в том числе принципы неопределенности Гейзенберга, логарифмический принцип и принцип неопределенности Назароса для неразделимого линейного канонического вейвлет-преобразования 7. 9.0011

Пример   2.

Для удобства вычислений ограничимся двумерным пространством. Из неравенства в уравнении (37) мы видим, что нижнюю границу можно соответствующим образом скорректировать, выбрав реальную свободную симплектическую матрицу M=(A,B:C,D) и анализирующую функцию ψ.

(и). Рассмотрим реальную свободную симплектическую матрицу

и двумерный вейвлет Морле ψ1(t), заданный выражением

. Тогда на основании уравнения (28) получаем

Следовательно, имеем

Принимая λ1=aπi и λ2=2a2, получаем

Реализация уравнения (41) в уравнении (30) дает

В частности, для (ω1,ω2)=(1,1), получаем

Следовательно, для любой нормированной функции f∈L2(R2) применение уравнения (42) к уравнению (37) дает нижнюю границу неравенства Гейзенберга в уравнении (37) в виде

(ii ). Рассмотрим реальную свободную симплектическую матрицу

и двумерный вейвлет DOG ψ2, заданный

Аналогично вычислениям, выполненным в (i), мы можем показать, что

(iii). Наконец, для реальной свободной симплектической матрицы

и двумерного вейвлета Maxican-hat ψ3

Константа допустимости Cψ3 и неравенство в уравнении (37) оказываются равными

Нижние границы неравенства неопределенности Гейзенберга в уравнении (37), соответствующие упомянутым выше параметрическим симплектическим матрицам и анализирующим функциям, сведены в табл. 2.

В нашей следующей теореме мы установим принцип логарифмической неопределенности для неразделимого линейного канонического вейвлет-преобразования в уравнении (14).

Принцип неопределенности Назарова измеряет локализацию нетривиальной функции f, принимая во внимание понятие носителя функции вместо дисперсии, используемой в неравенстве Гейзенберга–Паули–Вейля (38). В этом направлении справедлива следующая теорема.

4. Заключение

В настоящей статье мы ввели понятие ядра неразделимого линейного канонического вейвлет-преобразования в L2(Rn) для получения эффективного частотно-временного представления многомерных непереходных сигналов, которые имеет больше степеней свободы. Помимо изучения всех фундаментальных свойств, таких как теорема Рэлея, формула обращения и теорема о диапазоне, мы также сформулировали несколько неравенств неопределенностей для предлагаемого преобразования, содержащих неравенства Гейзенберга, логарифмическое неравенство и неравенство Назарова в несепарабельной линейной канонической области.

Авторские взносы

Написание первоначального чернового варианта, HMS; Концептуализация, методология, ФАС; Программное обеспечение и редактирование, Т.К.Г.; Методология и программное обеспечение, W.Z.L. и H.L.Q.; Финансирование приобретения и поддержка исследований, T.K.G. Все авторы прочитали и согласились с опубликованной версией рукописи.

Финансирование

Это исследование не получило внешнего финансирования.

Заявление Институционального контрольного совета

Неприменимо.

Заявление об информированном согласии

Не применимо.

Благодарности

Авторы глубоко признательны анонимным рецензентам за внимательное прочтение рукописи, указание на многие неточности и предоставление нескольких ценных предложений по улучшению первоначальной версии рукописи до современного уровня. Второй названный автор поддерживается SERB (DST), правительством Индии в рамках гранта № EMR/2016/007951.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. Мошинский М.; Кен, К. Линейные канонические преобразования и их унитарные представления. Дж. Матем. физ. 1971 , 12, 1772–1780. [Google Scholar] [CrossRef]
2. Сюй, Т.З.; Ли, Б.З. Линейное каноническое преобразование и его приложения; Science Press: Beijing, China, 2013. [Google Scholar]
3. Healy, J.J.; Кутай, Массачусетс; Озактас, HM; Шеридан, Дж.Т. Линейные канонические преобразования: теория и приложения; Springer: New York, NY, USA, 2016. [Google Scholar]
4. Чжан, З. Принцип неопределенности комплекснозначных функций в конкретных областях свободных метаплектических преобразований. Ж. Анал Фурье. заявл. 2021 , 27. [Google Scholar] [CrossRef]
5. Чжан, З. Принцип неопределенности для реальных функций в областях свободных метаплектических преобразований. Ж. Анал Фурье. заявл. 2019 , 25, 2899–2922. [Google Scholar] [CrossRef]
6. Госсон, М. Симплектическая геометрия и квантовая механика; Биркхойзер: Базель, Швейцария, 2006 г. [Google Scholar]
7. Цзин Р.; Лю, Б.; Ли, Р .; Лю, Р. N-мерный принцип неопределенности для свободного метаплектического преобразования. Математика 2020 , 8, 1685. [Google Scholar] [CrossRef]
8. «> Debnath, L.; Shah, FA Lectuer Notes on Wavelet Transforms; Birkhäuser: Boston, MA, USA, 2017. [Google Scholar]
9. Debnath, L.; Шах, Ф.А. Вейвлет-преобразования и их приложения; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
10. Dai, H.; Чжэн, З .; Ван, В. Новое дробное вейвлет-преобразование. коммун. Нелинейная наука. Число. Модел. 2017 , 44, 19–36. [Google Scholar] [CrossRef]
11. Wei, D.; Ли, Ю.М. Обобщенное вейвлет-преобразование на основе оператора свертки в области линейного канонического преобразования. Оптик 2014 , 125, 4491–4496. [Google Scholar] [CrossRef]
12. Ван, Дж.; Ван, Ю.; Ван, В .; Рен, С. Дискретное линейное каноническое вейвлет-преобразование и его приложения. EURASIP J. Adv. Сиг. Процесс. 2018 , 29, 1–18. [Google Scholar] [CrossRef][Green Version]
13. Shah, FA; Теали, А.А.; Тантари, А.Ю. Специальное аффинное вейвлет-преобразование и соответствующая формула суммирования Пуассона. Междунар. Дж. Вейвлеты Мультиразрешение. Инф. Процесс. 2021 , 19. [Google Scholar] [CrossRef]
14. Shah, FA; Тантари, А.Ю.; Заид, А.И. Специальные аффинные вейвлет-преобразования на основе свертки. Интегр. Транс. Спец.функц. 2020 , 1–21. [Google Scholar] [CrossRef]
15. Шах, Ф.А.; Теали, А.А.; Тантари, А.Ю. Линейные канонические вейвлет-преобразования в кватернионных доменах. Доп. заявл. Клиффорд Алгебр. 2021 , 31, 42. [Google Scholar] [CrossRef]
16. Shah, F.A.; Одинокий, В.З. Квадратично-фазовое вейвлет-преобразование с приложениями к обобщенным дифференциальным уравнениям. Мат. Методы Прил. науч. 2021 . принял. [Google Scholar] [CrossRef]
17. Antoine, JP; Муренци, Р.; Вандергейнст, П.; Список. Двумерные вейвлеты и их родственники; Издательство Кембриджского университета: Кембридж, Великобритания, 2004 г. [Google Scholar]
18. «> Pandey, JN; Пандей, Дж. С.; Упадхьяй, С.К.; Шривастава, Х.М. Непрерывное вейвлет-преобразование умеренных распределений Шварца в S ^‘ (R ⁿ ). Симметрия 2019 , 11, 235. [Google Scholar] [CrossRef][Green Version]
19. Шривастава, Х.М.; Шах, Ф.А.; Тантари, А.Ю. Семейство обобщенных преобразований Стоквелла на основе свертки. J. Псевдо-дифф. Опер. заявл. 2020 , 11, 1505–1536. [Google Scholar] [CrossRef]
20. Шривастава Х.М.; Сингх, А .; Рават, А .; Сингх, С. Семейство вейвлет-преобразований мексиканской шляпы, связанных с изометрией уравнения теплопроводности. Мат. Методы Прил. науч. 2021 , 44, 11340–11349. [Google Scholar] [CrossRef]
21. Али, С.Т.; Антуан, JP; Газо, Дж. П. Когерентные состояния, вейвлеты и их обобщения; Springer: New York, NY, USA, 2014. [Google Scholar]
22. Панди, Дж. Н.; Джа, Н.К.; Сингх, О.П. Непрерывное вейвлет-преобразование в n-мерном пространстве. Междунар. Дж. Вейвлеты Мультиразрешение. Инф. Процесс. 2016 , 14, 1650037. [Google Scholar] [CrossRef]
23. Folland, G.B.; Ситарам, А. Принцип неопределенности: математический обзор. Ж. Анал Фурье. заявл. 1997 , 3, 207–238. [Google Scholar] [CrossRef]
24. Cowling, M.G.; Прайс, Дж. Ф. Зависимость ширины полосы частот от концентрации времени: неравенство Гейзенберга-Паули-Вейля. СИАМ Дж. Матем. Анальный. 1994 , 15, 151–165. [Google Scholar] [CrossRef]
25. Неравенство Бекнера, У. Питта и принцип неопределенности. проц. Являюсь. Мат. соц. 1995 , 123, 1897–1905. [Google Scholar]
26. Wilczok, E. Новые принципы неопределенности для непрерывного преобразования Габора и непрерывного вейвлет-преобразования. Док. Мат. 2000 , 5, 201–226. [Google Scholar]
27. Шах, Ф.А.; Нисар, К.С.; Одинокий, WZ; Тантари, А.Ю. Принципы неопределенности для квадратично-фазовых преобразований Фурье. Мат. Методы Прил. науч. 2021 , 44, 10416–10431. [Google Scholar] [CrossRef]

Рисунок 1. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1/4.

Рисунок 1. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1/4.

Рисунок 2. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1.

Рисунок 2. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1.

Рисунок 3. ( a ) Частотное представление f, соответствующее позиции b=(0,0). ( b ) Частотное представление f, соответствующее позиции b=(1,1).

Рисунок 3. ( a ) Частотное представление f, соответствующее позиции b=(0,0). ( б ) Частотное представление f, соответствующее позиции b=(1,1).

Рисунок 4. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1/4.

Рисунок 4. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1/4.

Рисунок 5. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1.

Рисунок 5. Действительная и мнимая части неразделимого линейного канонического вейвлет-преобразования f, соответствующего фиксированному масштабу a=1.

Рисунок 6. ( a ) Частотное представление f, соответствующее позиции b=(0,0). ( b ) Частотное представление f, соответствующее позиции b=(1,1).

Рисунок 6. ( a ) Частотное представление f, соответствующее позиции b=(0,0). ( б ) Частотное представление f, соответствующее позиции b=(1,1).

Таблица 1. Некоторые частные случаи несепарабельного линейного канонического преобразования.

Таблица 1. Некоторые частные случаи несепарабельного линейного канонического преобразования.

9089..

Бесплатная симплектическая матрица M = A, B: C, D	Свободная метаплексная трансформация
• A = D = 0, B = –C = in	8	8	8
•  A=diag(a11,⋯,ann), B=diag(b11,⋯,bnn),
C=diag(c11,⋯,cnn), D=diag(d11,⋯ , DNN)	N-дивминный отдельный LCT
• A = D = DIAG (COSθ1, ⋯, COSθN),
B = –C = DIAG (SINOTIONS)	B = –C = DIAG (SINOTER)
B = –C = DIAG (SINOTRY)
B = –c = DIAG (SINOTE -мерный разделимый FrFT
•  A=D=Incosθ, B=−C=Insinθ	n-мерный неразделимый FrFT
•  A=D=In, B=diag(b11,⋯,bnn), C=0	n-мерный отделимый FrT
•  A=D=In, C=0	n-мерный безразмерный -разборный FrT

Таблица 2. Нижние оценки, связанные с неравенством Гейзенберга в уравнении (37).

Таблица 2. Нижние оценки, связанные с неравенством Гейзенберга в уравнении (37).

080909909090909 8040408

Симплектическая матрица	Константа допустимости Cψ	Lower Bound
	Cψ1=4π3π6	23π1/4
M1=A1,B1:C1,D1	Cψ2=6π111+3α21+α2	121/41+3α21+ α2
	Cψ3 = π5/221617	π321/4
	COVER = 4π3π6	COψ1 = 4π3		.