Крутящий момент двигателя постоянного тока Калькулятор

✖Постоянная двигателя постоянного тока — это постоянная величина, которую мы определяем для упрощения уравнения ЭДС машины постоянного тока.ⓘ Постоянная двигателя постоянного тока [K]			+10% -10%
✖Ток якоря двигателя постоянного тока определяется как ток якоря, развиваемый в электрическом двигателе постоянного тока из-за вращения ротора.ⓘ Двигатель постоянного тока с током якоря [Ia]		AbampereАмперАттоамперБайотсантиамперСГС ЭМБлок ЭС СГСДециамперДекаампереEMU текущегоESU текущегоExaampereФемтоамперГигаамперГилбертгектоамперкилоамперМегаампермикроамперМиллиампернаноамперПетаамперПикоамперStatampereтераамперЙоктоампереЙоттаампереZeptoampereZettaampere	+10% -10%
✖Магнитный поток (Φ) — это количество силовых линий магнитного поля, проходящих через магнитный сердечник электрического двигателя постоянного тока. ⓘ Магнитный поток [Φf]		Гаусс сантиметр²килолинЛинияКвант магнитного потокамаксвеллМегалайнМикровеберМилливеберТесла сантиметр²Тесла метр²блок полюсВольт-секундВебер	+10% -10%

✖Крутящий момент определяется как мера силы, которая заставляет ротор электрической машины вращаться вокруг оси.ⓘ Крутящий момент двигателя постоянного тока [Τ]

дина метрдина ммГрамм-сила-сантиметрграмм-сила-метрграмм-сила ммКилограмм-метрКилограмм-сила-сантиметрКилограмм-сила-метркгс ммКилоньютон-метрНьютон-сантиметрНьютон-метрНьютон Миллиметрунция силы-футУнция-сила-дюймфунт-сила футафунт силы дюйм

⎘ копия

👎

Формула

сбросить

👍

Крутящий момент двигателя постоянного тока Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. 2)*Сопротивление якоря)+Механические потери+Основные потери)/(Напряжение питания*(1-Общая электрическая эффективность)) Идти

ЭДС двигателя постоянного тока с использованием уравнения ЭДС

Наведенная противо-ЭДС = (Количество полюсов*Магнитный поток*Количество проводников*Скорость двигателя)/(60*Количество параллельных путей в машине постоянного тока) Идти

Крутящий момент якоря с учетом электрического КПД двигателя постоянного тока

Крутящий момент якоря = Двигатель постоянного тока с током якоря*Напряжение питания*Электрическая эффективность/Угловая скорость Идти

Напряжение при заданном электрическом КПД двигателя постоянного тока

Напряжение питания = Угловая скорость*Крутящий момент якоря/Двигатель постоянного тока с током якоря*Электрическая эффективность Идти

Ток якоря с учетом электрического КПД двигателя постоянного тока

Двигатель постоянного тока с током якоря = Угловая скорость*Крутящий момент якоря/Напряжение питания*Электрическая эффективность Идти

Шунтирующий ток возбуждения в двигателе постоянного тока

Шунтирующий ток возбуждения = Напряжение питания/Сопротивление шунтирующего поля Идти

Крутящий момент якоря с учетом механического КПД двигателя постоянного тока

Крутящий момент якоря = Механическая эффективность*крутящий момент Идти

Приведенный крутящий момент Механический КПД двигателя постоянного тока

крутящий момент = Крутящий момент якоря/Механическая эффективность Идти

Обратная ЭДС для условий максимальной мощности двигателя постоянного тока

Наведенная противо-ЭДС = Напряжение источника/2 Идти

Крутящий момент двигателя постоянного тока формула

крутящий момент = Постоянная двигателя постоянного тока*Двигатель постоянного тока с током якоря*Магнитный поток
Τ = K*I_a*Φ_f

Каков принцип работы двигателя постоянного тока?

Работа двигателя постоянного тока основана на том принципе, что когда проводник с током помещается в магнитное поле, на проводник действует механическая сила.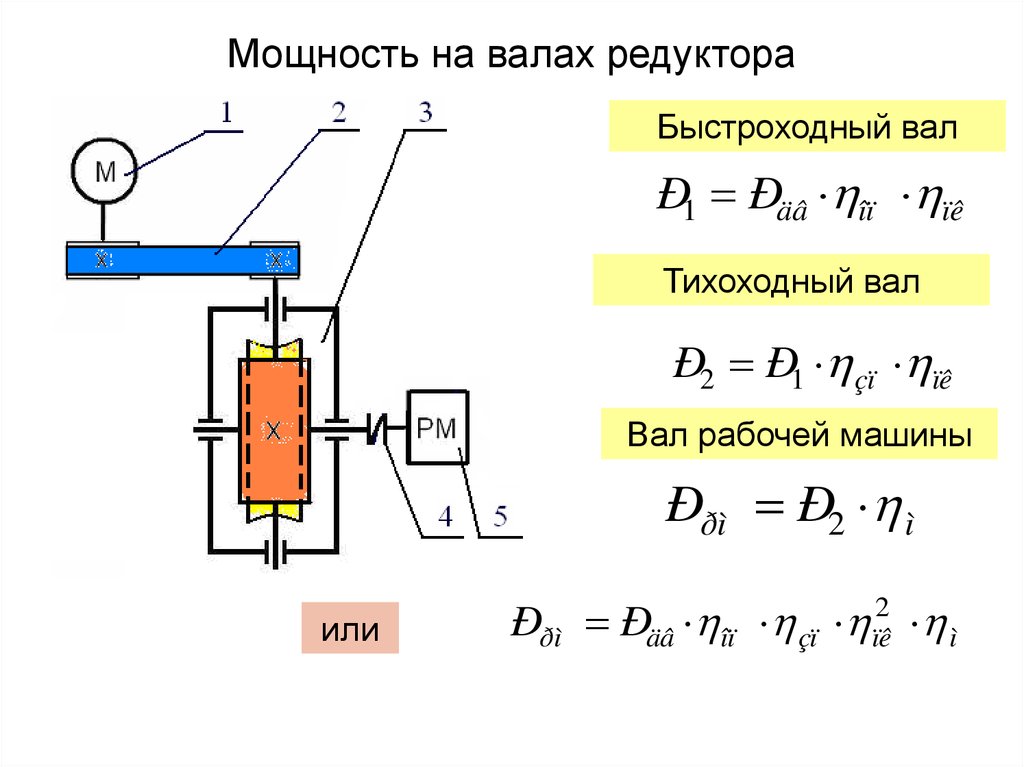

В принципе, конструктивных различий между двигателем постоянного тока и генератором постоянного тока нет.

Share

Copied!

Что такое крутящий момент

Крутящий момент двигателя является произведением силы на плечо рычага, к которому она прикладывается. Стоит напомнить, что сила измеряется в Ньютонах (Н), а плечо рычага в метрах (м). Расскажем о нем более подробно далее.

Очень многие автомобилисты не знают, что такое крутящий момент двигателя. На самом деле ответ на этот вопрос содержится еще в школьном курсе физики, но в свете того, что не все ее учили, а те, кто учил, не все поняли, а остальные просто забыли понятое, нет ничего удивительного, что этот вопрос остается открытым. Итак, что же такое крутящий момент двигателя?

Крутящий момент

Начать следует все же с физики. Крутящий момент двигателя является произведением силы на плечо рычага, к которому она прикладывается. Стоит напомнить, что сила измеряется в Ньютонах (Н), а плечо рычага в метрах (м). То есть один Нм равняется одному Ньютону (1Н), который приложен к метровому рычагу (1м).

В двигателе внутреннего сгорания сила передается от воспламеняющегося топлива поршню, от него к кривошипному механизму, а от него к коленвалу. Последний через систему трансмиссии и приводов и приводит колеса во вращение.

Разумеется, он не является постоянным и увеличивается, когда на плечо действует большая сила, и слабеет при ее уменьшении. Иными словами, когда водитель давит на «газ», то действующая на плечо сила возрастает и, соответственно, возрастает и крутящий момент.

Мощность двигателя

Крутящий момент имеет непосредственное отношение к мощности двигателя. Последняя, если говорить предельно просто, является совершенной за некоторую единицу времени работой. А поскольку работой двигателя и является тот самый крутящий момент, то мощность указывает на то, сколько раз за единицу времени двигателем был совершен крутящий момент.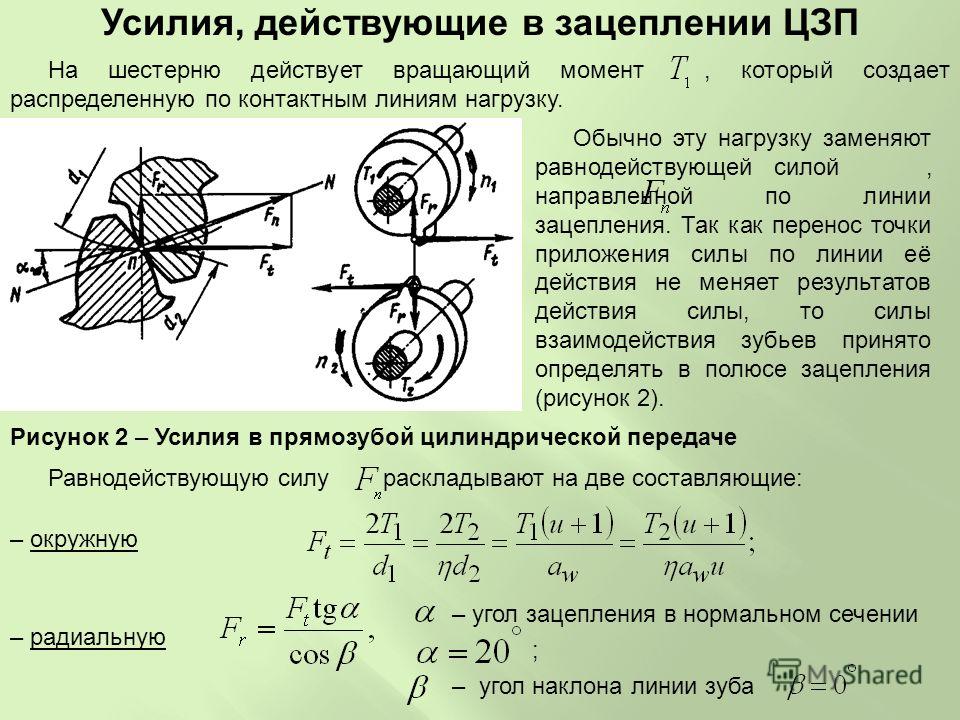

Физиками была создана формула, связывающая оба этих показателя:

Мощность (P) = момент крутящий (Мкр) * измеряемые в об./мин обороты двигателя (N)/9549.

Хотя мощность измеряется в киловаттах, в нашей стране они довольно сложны для автомобилистов, поэтому ее, как правило, измеряют в лошадиных силах (л.с.). Ничего сложного здесь нет, просто чтобы киловатты стали «лошадями», количество киловатт умножается на 1,36.

Крутящий момент и мощность

С каждым из этих компонентов вроде бы понятно, но на что влияет каждый из них? Мощность оказывает влияние на преодоление всевозможных сил, которые оказывают автомобилю противодействие. Таковыми являются силы качения колес, аэродинамические силы, и, конечно же, сила трения в трансмиссии, приводах машины, в самом двигателе и не только. И чем выше мощность двигателя, тем большее сопротивление машина в состоянии преодолеть и, соответственно, тем большую скорость разовьет.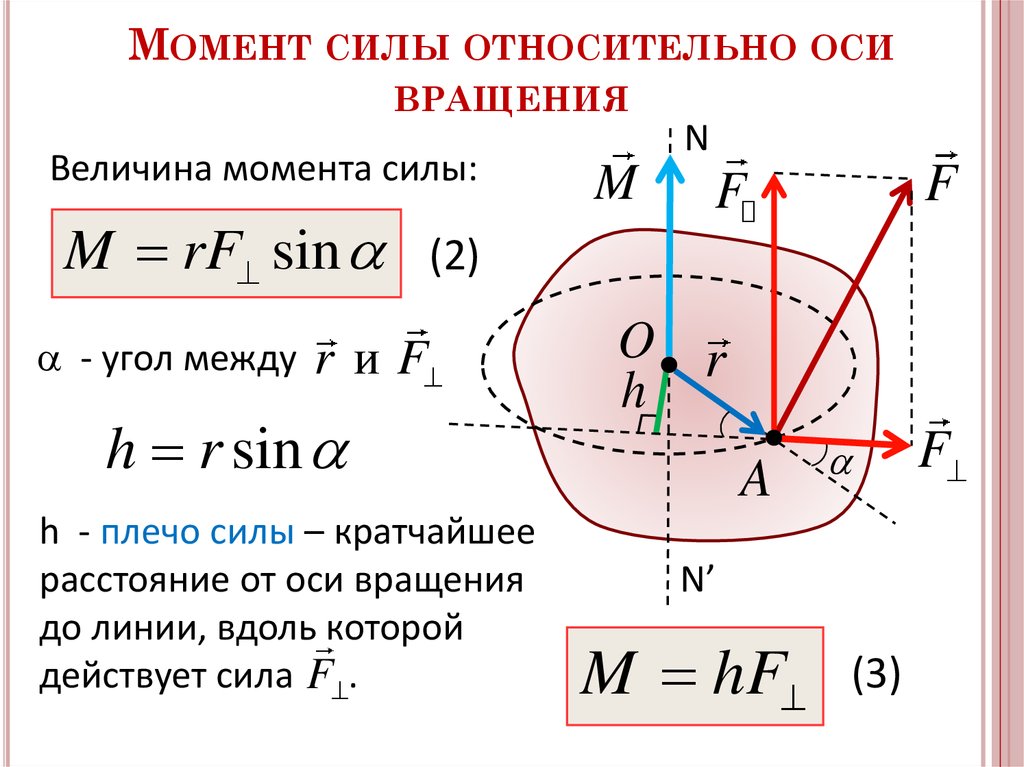 Однако мощность не является постоянной силой и сильно зависит от оборотов двигателя. Мощность на холостом ходу и на максимальных оборотах неодинакова. Поэтому многие автопроизводители указывают в технических характеристиках при каких оборотах достигается максимум мощности.

Здесь следует помнить, что максимальная мощность развивается не одномоментно, и с места машина стартует при минимальных оборотах, которые едва превышают холостой ход. Для того же чтобы мобилизировать максимум мощности необходим некоторый отрезок времени и именно здесь на сцену выходит крутящий момент. Именно он «решает» за какой временной промежуток автомобилем будет достигнута максимальная мощность. Проще говоря, динамика разгона автомобиля зависит именно от крутящего момента.

Бензиновые и дизельные двигатели

У бензиновых двигателей показатели не самые высокие. Своих почти максимальных значений бензиновый двигатель может достичь при оборотах, в среднем, 3-4 тысячи. Однако бензиновый двигатель способен быстро увеличивать мощность, и раскручиваться до семи и даже восьми тысяч оборотов. И если принять во внимание вышеприведенные формулы, то становится ясно, что при таких оборотах мощность может возрасти в несколько раз.

Что касается дизельных двигателей, то высокими оборотами они не обладают и как правило, их максимум составляет пять, а то и всего три тысячи оборотов. В этом отношении «дизель» однозначно проигрывает бензиновому двигателю. Но зато крутящий момент у дизельного двигателя в несколько раз превышает аналогичный показатель бензинового собрата и вдобавок он доступен почти с холостого хода.

Что важнее: крутящий момент или мощность?

Чтобы разобраться с этой задачей, можно привести несложный пример. Скажем, можно взять два двигателя от фирмы AUDI, один бензиновый 2.0 FSI (крутящий момент – 200 Нм, мощность – 150 л.с.), а другой дизельный (мощностью 140 л.с. и с крутящим моментом 320 Нм). После проведения тестирования в различных режимах оказывается, что дизельный двигатель мощнее бензинового двигателя в диапазоне от 1 до 4,5 тысяч оборотов. Причем мощность будет выше на 30, а то и на 40 «лошадей», что не мало.

Из этого следует, что обращать внимание исключительно на мощность не стоит, поскольку нередко менее объемный двигатель, имеющий более высокий крутящий момент, оказывается гораздо динамичнее, чем двигатель с низким крутящим моментом (пусть даже большого объема).

Подводя итоги можно сказать, что в корне неверно классифицировать автомобили ориентируясь исключительно на мощность (л.с.) двигателя. Кроме мощности необходимо учитывать еще и крутящий момент (Нм) поскольку если последний показатель будет намного выше, чем у другого автомобиля, то и двигатель у него будет значительно динамичнее.

10.7: Torque — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4032

• OpenStax
• OpenStax

Цели обучения

• Описать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
• Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
• Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент

Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.

Определение крутящего момента

До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси.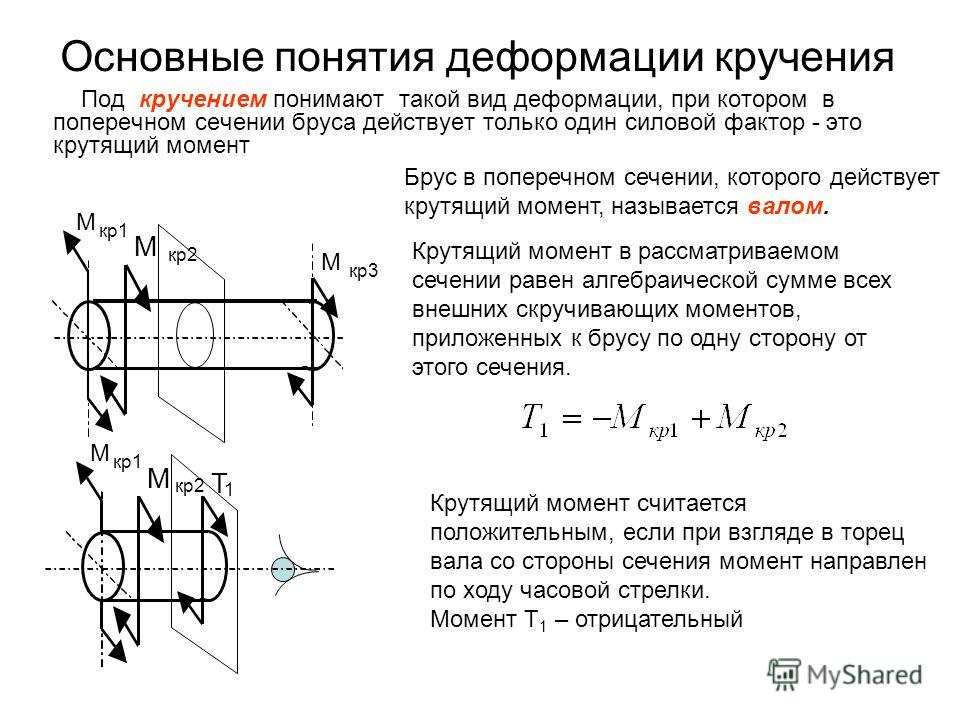 Мы называем этот вращательный аналог крутящим моментом .

В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.

Рисунок \(\PageIndex{1}\): Крутящий момент — это эффективность силы при повороте или скручивании, показанная здесь для вращения двери на петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Крутящий момент против часовой стрелки создается силой \(\vec{F}\), действующей на расстоянии r от шарниров (точки поворота). (b) Меньший крутящий момент против часовой стрелки создается, когда меньшая сила \(\vec{F}′\) действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (а), действующей на том же расстоянии, что и (а), но под углом \(\theta\), который меньше 90°.

Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.

Крутящий момент

Когда сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\) относительно точки O (рисунок \(\PageIndex{2}\)) , крутящий момент \(\vec{\tau}\) вокруг O равен

\[\vec{\tau} = \vec{r} \times \vec{F} \ldotp \label{10.22}\]

Рисунок \(\PageIndex{2}\): направление определяется по правилу правой руки.

Из определения векторного произведения крутящий момент \(\vec{\tau}\) перпендикулярен плоскости, содержащей \(\vec{r}\) и \(\vec{F}\), и имеет величина

\[|\vec{\tau}| = |\vec{r} \times \vec{F}| = rF \sin \theta,\]

, где \(\theta\) — угол между векторами \(\vec{r}\) и \(\vec{F}\). Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н • м. Величина r _\(\perp\) = rsin \(\theta\) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \(\vec{F}\), и называется Рычаг . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет

\[|\vec{\tau}| = r_{\perp} F \ldotp \label{10.23}\]

Перекрестное произведение \(\vec{r} \times \vec{F}\) также сообщает нам знак крутящего момента. На рисунке \(\PageIndex{2}\) векторное произведение \(\vec{r} \times \vec{F}\) расположено вдоль положительной оси z, что по соглашению представляет собой положительный крутящий момент. Если \(\vec{r} \times \vec{F}\) вдоль отрицательной оси z, это создает отрицательный крутящий момент.

Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на рисунке \(\PageIndex{3}\), мы увидим, как угол между радиусом \(\vec{r}\ ), а сила \(\vec{F}\) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол равен 90°, крутящий момент максимальный. Крутящий момент на рисунке \(\PageIndex{3}\) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z. Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.

Рисунок \(\PageIndex{3}\): Диск может свободно вращаться вокруг своей оси, проходящей через центр. Величина крутящего момента на диске равна rFsin \(\theta\). Когда \(\theta\) = 0°, крутящий момент равен нулю и диск не вращается. Когда \(\theta\) = 90°, крутящий момент максимален и диск вращается с максимальным угловым ускорением.

Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно указанной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:

\[\vec{\tau}_{net} = \sum_{i} |\vec{\tau}_{i}| \ldotp \label{10.24}\]

Расчет чистого крутящего момента для твердых тел на неподвижной оси

В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы вводим стратегию решения проблем.

Стратегия решения проблем: определение чистого крутящего момента

1. Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
2. Определите угол между плечом рычага \(\vec{r}\) и вектором силы.
3. Возьмите векторное произведение \(\vec{r}\) и \(\vec{F}\), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки вращения или оси.
4. Оценить величину крутящего момента с помощью r _\(\perp\) F.
5. Присвойте величине соответствующий знак, положительный или отрицательный.
6. Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.

Пример 10.14: Расчет крутящего момента

На рисунке \(\PageIndex{4}\) показаны четыре силы в определенных местах и ​​ориентациях по отношению к данной системе координат xy. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.

Рисунок \(\PageIndex{4}\): Четыре силы, создающие крутящие моменты.

Стратегия

Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение \(\vec{r}\) и вектора силы \(\vec{F}\).

Решение

Использование |\(\vec{\tau}\)| = r _\(\perp\) F = rFsin \(\theta\) для нахождения величины и \(\vec{r} = \vec{r} \times \vec{F}\) для определения знака крутящего момента.

Крутящий момент от силы 40 Н в первом квадранте определяется выражением (4)(40)sin 90° = 160 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н в третьем квадранте определяется выражением −(3)(20)sin 90° = − 60 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится на странице, поэтому оно отрицательно.

Крутящий момент от силы 30 Н в третьем квадранте определяется формулой (5)(30)sin 53° = 120 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1)(20)sin 30° = 10 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится за пределами страницы.

Таким образом, чистый крутящий момент равен \(\tau_{net} = \sum_{i} |\tau_{i}|\) = 160 − 60 + 120 + 10 = 230 Н • м.

Значение

Обратите внимание, что каждая сила, действующая против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.

Пример 10.15. Расчет крутящего момента на твердом теле

На рисунке \(\PageIndex{5}\) показано несколько сил, действующих в разных местах и ​​под разными углами на маховик. Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.

Рисунок \(\PageIndex{5}\): Три силы, действующие на маховик.

Стратегия

Мы рассчитываем каждый крутящий момент отдельно, используя перекрестное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \(\vec{F}_{1}\). Если мы посмотрим на рисунок \(\PageIndex{5}\), то увидим, что \(\vec{F}_{1}\) составляет угол 90° + 60° с радиус-вектором \(\vec{r }\). Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины: 9{о} = (-0,5\; m)(30\; N) = -15,0\; Н\; \cdotp m \ldotp\]

Когда мы оцениваем крутящий момент из-за \(\vec{F}_{3}\), мы видим, что угол, который он образует с \(\vec{r}\), равен нулю, поэтому \(\vec{r} \times \vec{F}_{3}\) = 0. Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.

Оцениваем сумму моментов:

\[\tau_{net} = \sum_{i} |\tau_{i}| = 5 — 15 = -10\; Н\; \cdotp m \ldotp\]

Значение

Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был зафиксирован на месте, \(\vec{F}_{3}\) вызвал бы перемещение маховика, а также \(\vec{F}_{1}\). Его движение было бы комбинацией поступательного движения и вращения.

Упражнение 10.6

Большое океанское судно садится на мель у береговой линии, как и Costa Concordia , и лежит под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы выровнять судно, чтобы поднять его на воду для транспортировки. Сила 5,0 x 10 ⁵ Н, действующая в точке А, должна быть приложена, чтобы выровнять судно. Каков крутящий момент в точке контакта корабля с землей (рис. \(\PageIndex{6}\))?

Рисунок \(\PageIndex{6}\): Судно садится на мель и наклоняется, что требует применения крутящего момента, чтобы вернуть судно в вертикальное положение.

---

Эта страница под названием 10.7: Torque распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. рычаг
   2. источник@https://openstax.