Кинематические схемы шестеренных дифференциалов. Работа дифференциала при движении автомобиля. Распределение моментов
Машиностроение \ Конструкция, расчет и потребительские свойства изделий
Страницы работы
17 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
Дифференциал
Механизм трансмиссии, распределяющий крутящий момент двигателя между ведущими колесами и ведущими мостами автомобиля, называется дифференциалом.
Дифференциал служит для обеспечения ведущим колесам разной скорости вращения при движении автомобиля по неровным дорогам и на поворотах.
Разная скорость вращения ведущим колесам, проходящим разный путь на поворотах и неровных дорогах, необходима для их качения без скольжения и буксования. В противном случае повысится сопротивление движению автомобиля, увеличатся расход топлива и износ шин.
В зависимости от типа и назначения автомобилей на них применяются различные типы дифференциалов (рис. ).
В противном случае повысится сопротивление движению автомобиля, увеличатся расход топлива и износ шин.
В зависимости от типа и назначения автомобилей на них применяются различные типы дифференциалов (рис. ).
Дифференциал, распределяющий крутящий момент двигателя между ведущими колесами автомобиля, называется межколесным. Дифференциал, который распределяет крутящий момент двигателя между ведущими мостами автомобиля, называется межосевым. На большинстве автомобилей применяются конические дифференциалы, симметричные и малого трения.
Симметричный дифференциал распределяет поровну крутящий момент. Его передаточное число равно единице (uд=1), т. е, полуосевые шестерни 3 и 4 (рис., а, б) имеют одинаковые диаметры и равное число зубьев. Симметричные дифференциалы применяются на автомобилях обычно в качестве межколесных и реже — межосевых, когда необходимо распределять крутящий момент поровну между ведущими мостами. Симметричные дифференциалы применяются на автомобилях обычно в качестве межколесных и реже — межосевых, когда необходимо распределять крутящий момент поровну между ведущими мостами.
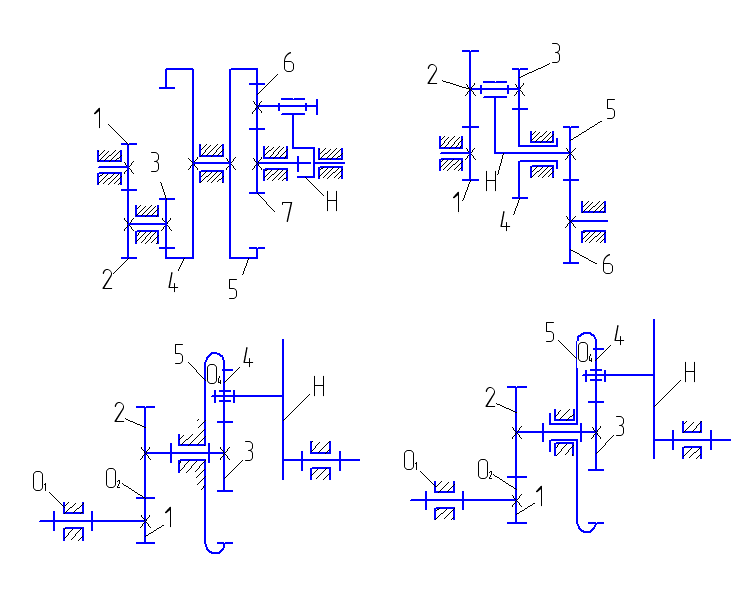
Кинематические схемы шестеренных дифференциалов а, б — симметричных; в, г — несимметричных; 1 — корпус; 2 — сателлит; 3, 4 – шестерни
Несимметричный дифференциал (рис. в,г) распределяет не поровну крутящий момент. Его передаточное число не равно единице, но постоянно (uд≠1=const), т.е. полуосевые шестерни 3 и 4 имеют неодинаковые диаметры и разное число зубьев. Несимметричные дифференциалы применяют, как правило, в качестве межосевых, когда необходимо распределять крутящий момент пропорционально нагрузкам, приходящимся на ведущие мосты.
Межколесный конический симметричный дифференциал (см., а) состоит из корпуса 1, сателлитов 2, полуосевых шестерен 3 и 4, которые соединены полуосями с ведущими колесами автомобиля. Дифференциал легкового автомобиля имеет два свободно вращающихся сателлита, установленных на оси, закрепленной в корпусе дифференциала, а у грузового автомобиля — четыре сателлита, размещенных на шипах крестовины, также закрепленной в корпусе дифференциала.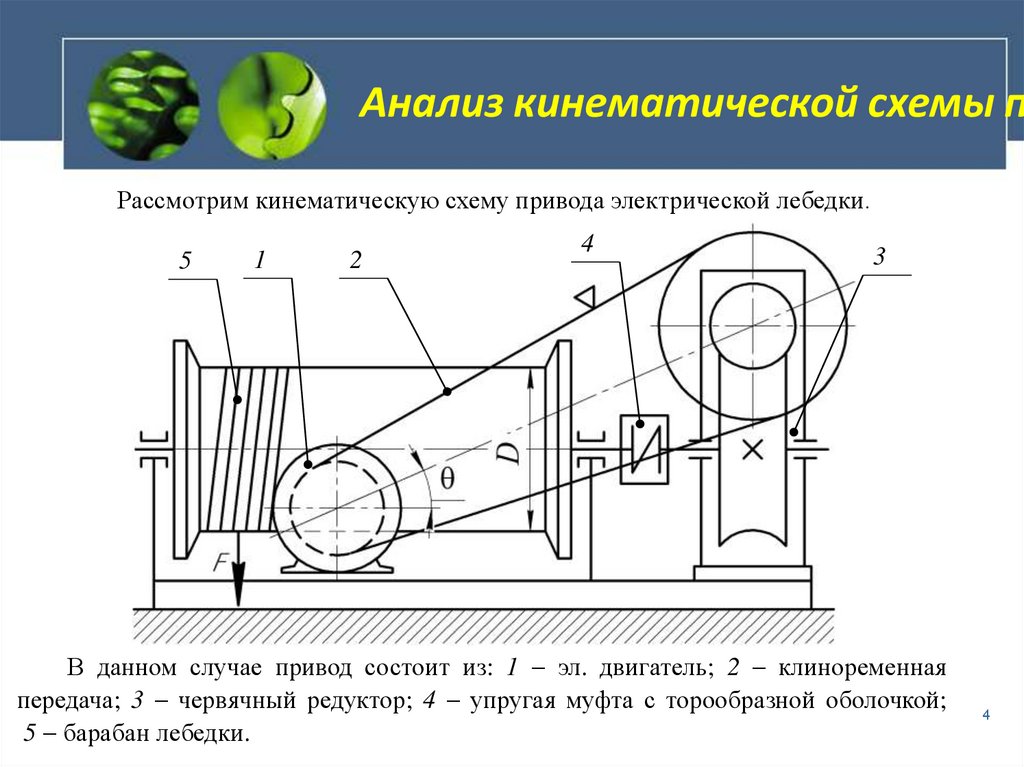
При этом корпус дифференциала, сателлиты и полуосевые шестерни вращаются как одно целое. В этом случае сателлиты 3 не вращаются вокруг своих осей, заклинивают полуосевые шестерни 4 и на оба ведущих колеса передаются одинаковые крутящие моменты.
Работа дифференциала при движении автомобиля: а — по прямой; б — на повороте; 1, 4 — шестерни; 2 — корпус; 3 — сателлит; 5 – полуось
При повороте автомобиля (рис., б) внутреннее по отношению к центру поворота колесо встречает большее
Похожие материалы
Информация о работе
Скачать файл
Кинематическая схема распределителя
Категория:
Машины для укладки асфальта
Публикация:
Кинематическая схема распределителя
Читать далее:
Устройство распределителя
Кинематическая схема распределителя
Мощность от двигателя (рис. 34) передается сцеплению двигателя. При включенном рычаге сцепления через диски сцепления мощность передается валу, на котором закреплена шестерня ходоуменьшителя. Шестерня на одном конце имеет полумуфту и может передвигаться по валу. Ходоуменьшитель состоит из двух пар шестерен. Управление ходоуменьшителем осуществляется рычагом, который передвигает шестерню с полумуфтой по валу. При включенном ходоуменьшителе шестерня соединяется с шестерней ходоуменьшителя, которая закреплена на валу. На этом же валу закреплена шестерня, которая имеет постоянное зацепление с шестерней. При отключенном ходоуменьшителе полумуфта шестерни входит в зацепление в полумуфту шестерни. Шестерня сидит на валу. На другом конце вала закреплена коническая шестерня, передающая крутящий момент на конические шестерни реверса. Управление реверсом осуществляется при помощи рычага И, который может соединять одну из цилиндрических шестерен блока конических шестерен реверса с цилиндрической шестерней, сидящей на валу. На валу жестко закреплены две шестерни к два блока шестерен, которые могут передвигаться по валу в осевом направлении.
34) передается сцеплению двигателя. При включенном рычаге сцепления через диски сцепления мощность передается валу, на котором закреплена шестерня ходоуменьшителя. Шестерня на одном конце имеет полумуфту и может передвигаться по валу. Ходоуменьшитель состоит из двух пар шестерен. Управление ходоуменьшителем осуществляется рычагом, который передвигает шестерню с полумуфтой по валу. При включенном ходоуменьшителе шестерня соединяется с шестерней ходоуменьшителя, которая закреплена на валу. На этом же валу закреплена шестерня, которая имеет постоянное зацепление с шестерней. При отключенном ходоуменьшителе полумуфта шестерни входит в зацепление в полумуфту шестерни. Шестерня сидит на валу. На другом конце вала закреплена коническая шестерня, передающая крутящий момент на конические шестерни реверса. Управление реверсом осуществляется при помощи рычага И, который может соединять одну из цилиндрических шестерен блока конических шестерен реверса с цилиндрической шестерней, сидящей на валу. На валу жестко закреплены две шестерни к два блока шестерен, которые могут передвигаться по валу в осевом направлении.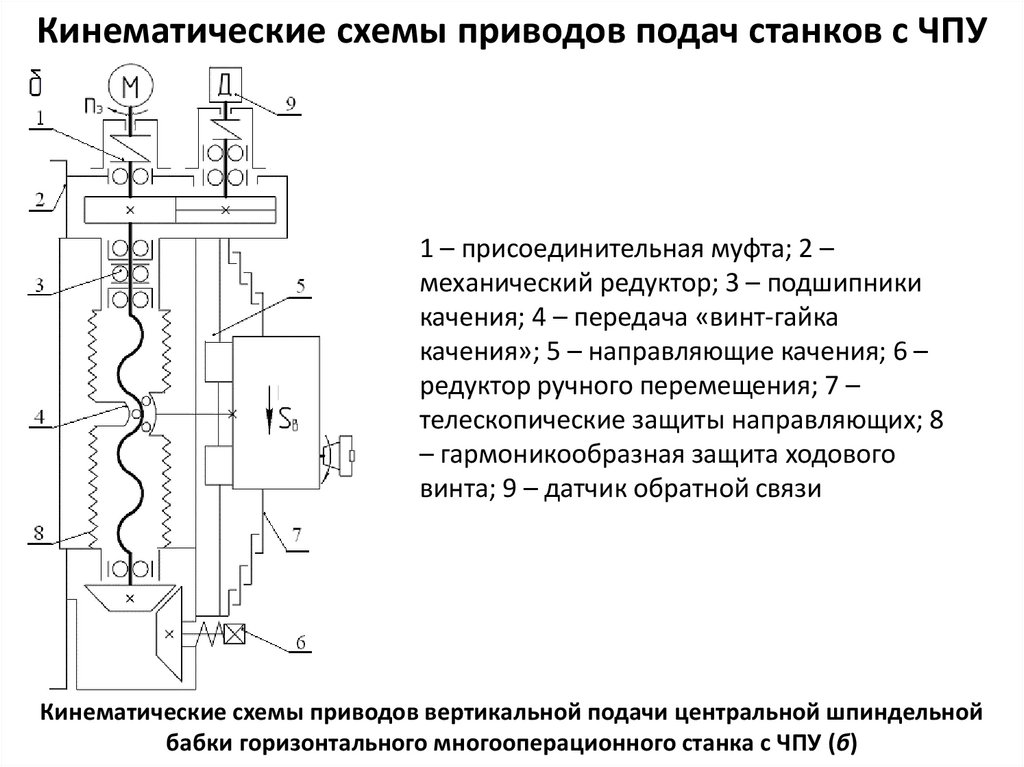
Гусеничная лента вместе с приводной звездочкой преобразует вращательное движение в поступательное. Гусеничная лента с другого конца поддерживается в натянутом состоянии ведомой звездочкой. Так передается мощность на движение правой гусенице укладчика. Аналогично после дифференциала мощность передается и левой гусенице, поэтому описание передачи мощности на левую гусеницу не приводится.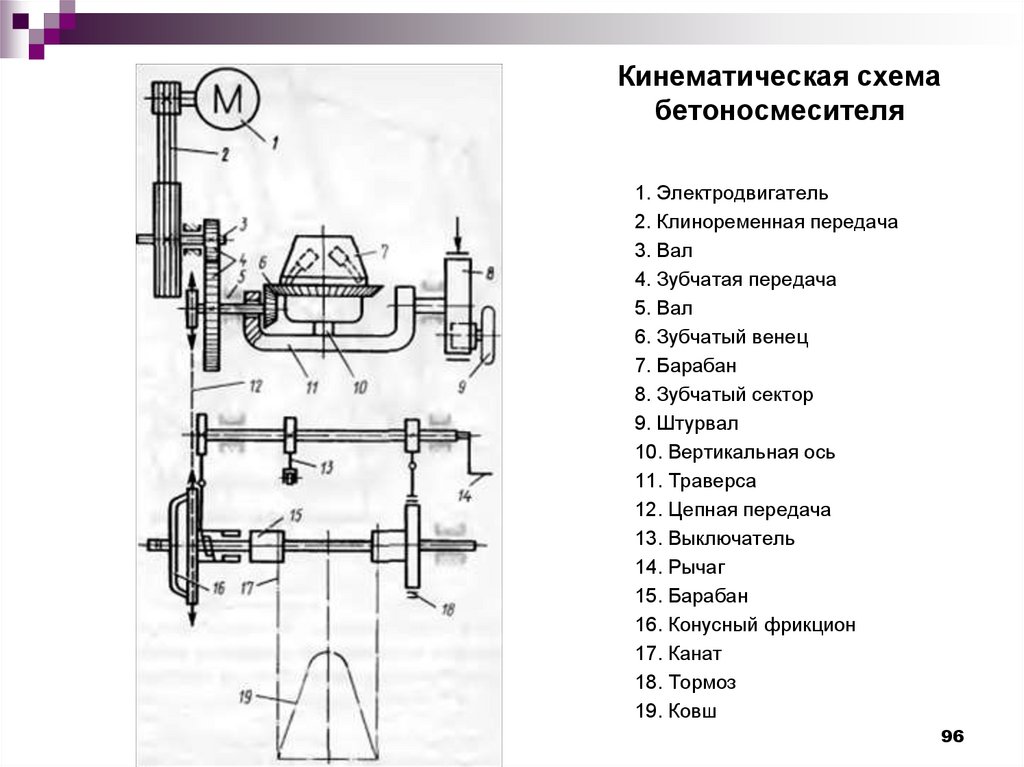
При включении II передачи мощность от вала к венцовой шестерне дифференциала передается через блок шестерни валу и далее через блок-шестерню венцовой шестерне дифференциала.
Рекламные предложения на основе ваших интересов:
Дополнительные материалы по теме:
Включением блок-шестерни с блок-шестерней получают III передачу передвижения распределителя.
Получение IV передачи распределителя осуществляется путем включения шестерни с шестерней, V —от включения блок-шестерни с шестерней, а VI — при включении блок-шестерни с шестерней.
Все указанные шесть скоростей распределителя являются рабочими.
При транспортировании распределителя включается его наивысшая скорость — 2 км/ч. Передача мощности при этом осуществляется следующим образом: рычагом управления сцепления двигателя включают муфту сцепления с задними дисками. Через эти диски мощность двигателя передается на полый вал с шестерней, которая находится в постоянном зацеплении с другой цилиндрической блок-шестерней.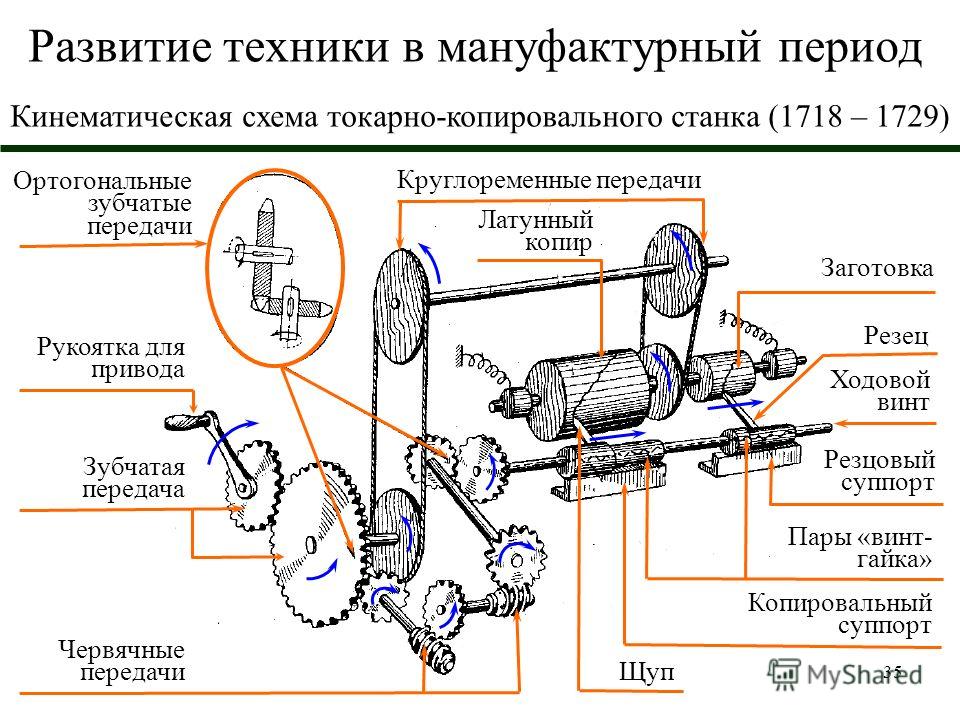
Рис. 34. Кинематическая схема асфальтоукладчика ДС-54:
1— вал гидронасоса НШ-10; 2 — двигатель; 3 — сцепление; 4 — вал; 5, 7, S, 49 — шестерни ходоуменьшителя; 6 — вал ходоуменыпителя; 9, 13, 17, 20, 24, 28, 46, 53 — вал; 10 — коническая шестерня; 11 — блок-шестерня включения V и VI передач; 12 — блок-шестерня включения II и III передач; 14 — шестерня включения IV передачи; 15 — шестерня включения I передачи; 16 — шестерня; 18, 19 — шестерни заднего хода; 21 — звездочка привода гусеничного хода; 22 — ведущая звездочка гусеничного хода; 23, 25, 27 — звездочки привода гусеничного хода; 26 — цепь привода гусеничного хода; 29, 30 — шестерни привода гусеничного хода; 31 — тормозной барабан; 32 — вал-полуось; 33 — полумуфта блокировки дифференциала; 35, 49, 57 — шестерни: 36 — дифференциал; 37 — венцовая шестерня дифференциала; 38 — сателлит; 39, 40, 56 — блок шестерни; 41 — шестерня включения VI передачи; 42 — коническая шестерня блока шестерен; 43, 58 — реверс; 44, 45 — коническая шестерня; 47 — блок-шестерня реверса; 48 — гидронасос НШ-67; 50, 51 — шестерня привода гидронасо-са; 52 — блок-шестерня привода гидронасоса; 54, 55 — конические шестерни привода гидронасоса, 59 — малая шестерня; 60 — большая шестерня; 61—диск сцепления; 62, 63 — шестерни привода гидронасоса НШ-10;
А — рычаг включения гидронасоса НО-Ю; Б — рычаг включения муфты сцепления двигателя; В — рычаг управления коробкой передач; Г — рычаг тормоза правой гусеницы; Д — рычаг включения блокировки дифференциала; Е — рычаг тормоза левой гусеницы; И — рычаг управления реверсом; К — рычаг включения гидронасоса HIII-67; Л — рычаг включения ходоуменьшителя
Кроме передачи мощности на передвижение распределителя, от дизельного двигателя отбирается часть мощности для привода двух гидронасосов НШ-10 и НШ-67.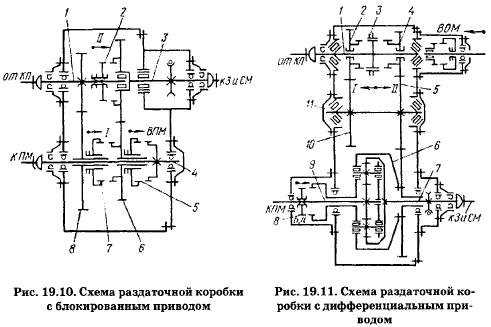 Привод гидронасоса НШ-67 осуществляется поворотом рычага К, включающим блок-шестерню с шестерней, при этом вращение блока-шестерни будет передаваться конической шестерне через вал, на котором они обе находятся.
Привод гидронасоса НШ-67 осуществляется поворотом рычага К, включающим блок-шестерню с шестерней, при этом вращение блока-шестерни будет передаваться конической шестерне через вал, на котором они обе находятся.
Коническая шестерня находится в постоянном зацеплении с конической шестерней, сидящей на валу совместно с цилиндрической шестерней. Крутящий момент с цилиндрической шестерни передается через промежуточную шестерню на шестерню, сидящую на валу гидронасоса. Гидронасос подает масло в систему под давлением для привода гидромотора рабочих органов.
Второй гидронасос НШ-10 приводится в действие от распределительной шестерни дизельного двигателя через промежуточную цилиндрическую шестерню 63 на шестерню, сидящую на шариковой муфте вала гидронасоса. Управление включением гидронасоса производится рычагом А, который включает или выключает шариковую муфту.
Гидронасос НШ-10 подает масло в гидроцилиндры подъема и опускания рамы рабочих органов, подъема и опускания боковых стенок приемного бункера, а при укладке цементобетонных смесей служит для поворота рамы рабочих органов.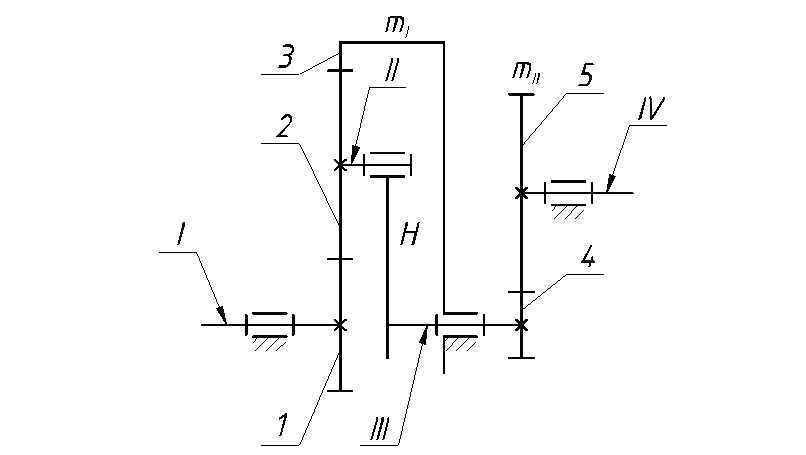
При укладке асфальтобетонных покрытий гидромотором (рис. 35) типа ПМ-5 приводится в действие генератор 3Г-105 через клиноременную передачу, состоящую из двух шкивов, закрепленных один на распределительном валу, а другой — на валу генератора. Кроме того, на распределительном валу закреплен шкив клиноременной передачи, при помощи которой мощность передается эксцентриковому валу, соединенному при помощи шатунов с трамбующим брусом. При этом трамбующий брус будет производить возвратно-поступательное движение, уплотняя асфальтобетонную смесь. При оборотах гидромотора 1380 об/мин трамбующий брус будет производить 1100 кол/мин, а генератор около 2000 об/мин.
При укладке бетонной смеси мощность от гидромотора (рис. 36) передается через кли-ноременную передачу на промежуточный вал, с которого крутящий момент второй клиноременной передачей передается на распределительный вал. С распределительного вала часть мощности через гибкие сочленения передается виброплитам, а часть через третью клиноременную передачу передается вибратору.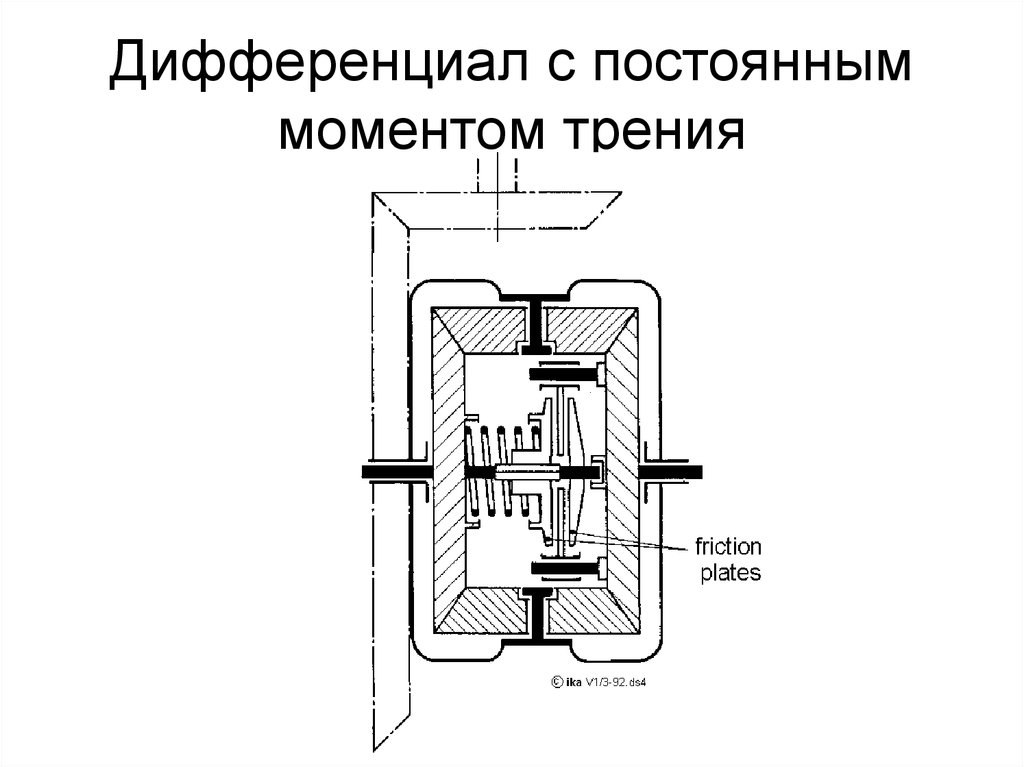
При оборотах вала гидромотора ПМ-5, равным 1380 об/мин, вибраторы имеют 3600 кол/мин.
Распределитель является самоходной машиной на гусеничном ходу. Машина имеет сменные рабочие органы, позволяющие укладывать асфальтобетонные смеси и щебень. Для укладки щебня на машине устанавливаются виброплиты, уплотняющие распределяемый щебень, а выглаживающая плита с системой подогрева заменяется опорной плитой.
При распределении цементобетонных смесей и цементогрунта на машине устанавливается специальный рабочий орган. В зависимости от вида распределяемого материала укладчик должен передвигаться по песчаному или твердому основанию. Для обеспечения необходимого тягового усилия при работе по распределению материалов укладчик имеет два комплекта сменных гусеничных лент. Для передвижения укладчика по песчаному основанию используются гусеничные ленты с башмаками высотой 60 мм.
Рис. 35. Кинематическая схема привода трамбующего бруса асфальтоукладчика
Рис. 36. Кинематическая схема привода вибраторов
36. Кинематическая схема привода вибраторов
Дифференциальная кинематика | SpringerLink
L. Sciavicco, B. Siciliano, Моделирование и управление роботами-манипуляторами (Springer Science & Business Media, London, 2000)
CrossRef МАТЕМАТИКА Google Scholar
Р. Фезерстоун, Алгоритмы динамики твердого тела (Springer, Boston, 2008)
CrossRef МАТЕМАТИКА Google Scholar
Дж. Денавит, Р. Хартенберг, Кинематическая запись для механизмов младших пар на основе матриц. Транс. КАК Я. Дж. Заявл. мех. 22 , 215–221 (1955)
MathSciNet МАТЕМАТИКА Google Scholar
Р.М. Мюррей, З. Ли, С.С. Састри, Математическое введение в роботизированные манипуляции (CRC Press, Бока-Ратон, 1994)
МАТЕМАТИКА Google Scholar
- «>
Дж. Юань, Управление манипулятором с обратной связью с использованием кватернионной обратной связи. IEEE Дж. Робот. автомат. 4 (4), 434–440 (1988)
CrossRef Google Scholar
Х. Г. Кватни, Г. Бланкеншип, Нелинейное управление и аналитическая механика: вычислительный подход (Springer, New York/Birkhauser, 2000)
CrossRef МАТЕМАТИКА Google Scholar
Г. Странг, Линейная алгебра и ее приложения , Cengage Learning, 4-е изд., 19 июля 2005 г.
Google Scholar
К. Кройц-Дельгадо, М. Лонг, Х. Сераджи, Кинематический анализ манипуляторов с 7 степенями свободы. Междунар. Дж. Робот. Рез. 11 (5), 469–481 (1992)
CrossRef Google Scholar
- «>
А. Секигучи, Ю. Атобе, К. Камета, Д. Ненчев, Ю. Цумаки, О генерации движения гуманоидного робота с помощью SC-подхода, в Ежегодная конференция Японского общества робототехники , том. 2, 2003, с. 2А27
Google Scholar
Ю. Огура, Х.-О. Лим, А. Таканиши, Генерация растянутой модели ходьбы для двуногого робота-гуманоида, в IEEE/RSJ International Conference on Intelligent Robots and Systems , 2003, стр. 352–357
. Google Scholar
Р. Куразуме, С. Танака, М. Ямасита, Т. Хасегава, К. Йонеда, Ходьба двуногого робота на прямых ногах, в 2005 Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , том. 2 (IEEE, 2005), стр. 337–343
Google Scholar
М. Морисава, С. Кадзита, К. Канеко, К. Харада, Ф.
 Канехиро, К. Фудживара, Х. Хирукава, Генерация шаблона двуногого хождения, ограниченного параметрической поверхностью, в IEEE International Conference on Robotics and Автоматика , 2005, стр. 2405–2410
Канехиро, К. Фудживара, Х. Хирукава, Генерация шаблона двуногого хождения, ограниченного параметрической поверхностью, в IEEE International Conference on Robotics and Автоматика , 2005, стр. 2405–2410Google Scholar
К. Камета, А. Сэкигучи, Ю. Цумаки, Д. Ненчев, Управление ходьбой с использованием подхода SC для роботов-гуманоидов, в Международная конференция IEEE-RAS по роботам-гуманоидам , 2005 г., стр. 289–294
Google Scholar
К. Такахаши, М. Нода, Д. Ненчев, Ю. Цумаки, А. Секигути, Статическая прогулка гуманоидного робота на основе метода согласованности с сингулярностью, в IEEE/RSJ Международная конференция по интеллектуальным роботам и системам , 2006, стр. 5484–5489
Google Scholar
К. Камета, А.
 Сэкигучи, Ю. Цумаки, Ю. Канамия, Управление ходьбой вокруг сингулярности с использованием сферического перевернутого маятника с опорой под полом, в IEEE-RAS International Conference on Humanoid Robots , 2007, стр. 210–215
Сэкигучи, Ю. Цумаки, Ю. Канамия, Управление ходьбой вокруг сингулярности с использованием сферического перевернутого маятника с опорой под полом, в IEEE-RAS International Conference on Humanoid Robots , 2007, стр. 210–215Google Scholar
Н. Хандхару, Дж. Юн, Г. Ким, Генерация модели походки с растяжкой колена для двуногого робота с использованием пальцевых и пяточных суставов, в Международная конференция IEEE-RAS по роботам-гуманоидам , Тэджон, Корея, 2008 г., стр. 265–270
Google Scholar
З. Ли, Н.Г. Цагарикис, Д.Г. Колдуэлл, Б. Вандерборхт, Генерация траектории ходьбы с выпрямленным коленом для робота-гуманоида iCub, в Международная конференция IEEE по управлению, автоматизации, робототехнике и зрению , 2010, стр. 2355–2360
Google Scholar
- «>
Ю. Харада, Дж. Такахаши, Д. Ненчев, Д. Сато, Ходьба на основе предельного цикла трехмерного двуногого 7DoF с плоскостопием, в 2010 Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , октябрь 2010. С. 3623–3628
. Google Scholar
С. Котосака, Х. Отаки, Выборочное использование исполнительного механизма для робота-гуманоида с помощью единственной конфигурации. Дж. Робот. соц. Япония. 25 (8), 115–121 (2007)
Перекрёстная ссылка Google Scholar
Х. Арисуми, С. Миоссек, Ж.-Р. Шардонне, К. Йокои, Динамический подъем за счет движения всего тела роботов-гуманоидов, Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , 2008 г., 2008 г., стр. 668–675
Google Scholar
К.
 Левенберг, Метод решения некоторых нелинейных задач методом наименьших квадратов. Q.J. Appl. Мат. II (2), 164–168 (1944)
Левенберг, Метод решения некоторых нелинейных задач методом наименьших квадратов. Q.J. Appl. Мат. II (2), 164–168 (1944)Google Scholar
Ю. Накамура, Х. Ханафуса, Решения обратной кинематики с устойчивостью к сингулярностям для управления роботом-манипулятором. Дж. Дин. Сист. Meas Control 108 (3), 163 (1986)
Google Scholar
CW Wampler, Обратные кинематические решения манипулятора, основанные на векторных формулировках и демпфированных методах наименьших квадратов. IEEE транс. Сист. Человек Киберн. 16 (1), 93–101 (1986)
CrossRef МАТЕМАТИКА Google Scholar
Т. Сугихара, Независимая от разрешимости обратная кинематика методом Левенберга-Марквардта. IEEE транс. Робот. 27 (5), 984–991 (2011)
CrossRef Google Scholar
- «>
Д. Ненчев, Отслеживание траекторий манипулятора с обычными сингулярностями: нуль-космический подход. Междунар. Дж. Робот. Рез. 14 (4), 399–404 (1995)
CrossRef Google Scholar
Д. Ненчев, Ю. Цумаки, М. Утияма, Параметризация движения и управления роботом, согласующаяся с сингулярностью. Междунар. Дж. Робот. Рез. 19 (2), 159–182 (2000)
CrossRef Google Scholar
С. Таки, Д. Ненчев, Новая инверсная кинематическая декомпозиция, совместимая с сингулярностью, для манипуляторов типа S-R-S, в Международная конференция IEEE по робототехнике и автоматизации , Гонконг, Китай, 2014 г., стр. 5070–5075
Google Scholar
Ю. Цумаки, Д. Ненчев, С. Котера, М. Утияма, Телеоперация на основе сопряженного подхода Якоби. Система управления IEEE.
 Маг. 17 (1), 53–62 (1997)
Маг. 17 (1), 53–62 (1997)CrossRef Google Scholar
Г.Х. Голуб, С.Ф. Ван Лоан, Матричные вычисления (Издательство Университета Джона Хопкинса, Балтимор, 1996)
МАТЕМАТИКА Google Scholar
А.А. Мацеевский, С.А. Кляйн, Разложение по сингулярным числам: вычисления и приложения к робототехнике. Междунар. Дж. Робот. Рез. 8 (6), 63–79 (1989)
CrossRef Google Scholar
Т. Йошикава, Управление роботизированными механизмами. Междунар. Дж. Робот. Рез. 4 (2), 3–9 (1985)
CrossRef Google Scholar
Ю. Огура, Х. Айкава, К. Симомура, Х. Кондо, А. Моришима, Х.-О. Лим, А. Таканиши, Разработка нового робота-гуманоида WABIAN-2, Международная конференция IEEE по робототехнике и автоматизации , 2006 г.
 , стр. 76–81
, стр. 76–81Google Scholar
Т. Уимбок, Д. Ненчев, А. Альбу-Шаффер, Г. Хирцингер, Экспериментальное исследование динамических безреактивных движений гуманоидного робота Джастина DLR, в Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , 2009 г. (IEEE, Сент-Луис, 2009 г.), стр. 5481–5486
CrossRef Google Scholar
К. Канеко, Ф. Канехиро, М. Морисава, К. Акачи, Г. Миямори, А. Хаяси, Н. Канехира, Гуманоидный робот HRP-4 – гуманоидная робототехническая платформа с легким и тонким телом, в IEEE Международная конференция по интеллектуальным роботам и системам , 2011 г., стр. 4400–4407
Google Scholar
И.-В. Парк, Дж.-Ю. Ким, Дж. Ли, Дж.-Х. О, механическая конструкция гуманоидной роботизированной платформы HUBO.
 Доп. Робот. 21 (11), 1305–1322 (2007)
Доп. Робот. 21 (11), 1305–1322 (2007)CrossRef Google Scholar
М. Цукер, С. Джу, М. Грей, К. Расмуссен, Э. Хуанг, М. Стилман, А. Бобик, Система общего назначения для дистанционного управления роботом-гуманоидом DRC-HUBO. Дж. Полевой робот. 32 (3), 336–351 (2015)
CrossRef Google Scholar
Т. Бушманн, С. Ломайер, Х. Ульбрих, Робот-гуманоид Лола: дизайн и управление ходьбой. Дж. Физиол. Париж 103 (3–5), 141–148 (2009)
CrossRef МАТЕМАТИКА Google Scholar
А. Бен-Исраэль, Т.Н. Greville, Обобщенные инверсии — теория и приложения . Книги CMS по математике, 2-е изд. (Спрингер, Нью-Йорк, 2003 г.)
Google Scholar
А.
 Льежуа, Автоматическое диспетчерское управление конфигурацией и поведением многотельных механизмов. IEEE транс. Сист. Человек Киберн. 7 (12), 868–871 (1977)
Льежуа, Автоматическое диспетчерское управление конфигурацией и поведением многотельных механизмов. IEEE транс. Сист. Человек Киберн. 7 (12), 868–871 (1977)CrossRef МАТЕМАТИКА Google Scholar
Ю. Накамура, Advanced Robotics: Redundancy and Optimization (Addison-Wesley Publishing Company, Reading, 1991)
Google Scholar
Т. Асфур, Р. Диллманн, Человекоподобное движение гуманоидного робота-манипулятора на основе решения обратной кинематической задачи в закрытой форме, в Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , Лас-Вегас (IEEE, 2003), стр. 1407–1412
Google Scholar
М. Симидзу, Х. Какуя, В.-К. Юн, К. Китагаки, К. Косугэ, Аналитическое обратное кинематическое вычисление для избыточных манипуляторов с 7 степенями свободы с совместными пределами и его применение для разрешения избыточности.
 IEEE транс. Робот. 24 (5), 1131–1142 (2008)
IEEE транс. Робот. 24 (5), 1131–1142 (2008)CrossRef Google Scholar
Р.К. Луо, Т.-В. Лин, Ю.-Х. Цай, Аналитическое инверсионное кинематическое решение для модульных резервных манипуляторов с 7 степенями свободы со смещениями на плече и запястье, в IEEE/RSJ International Conference on Intelligent Robots and Systems , Чикаго, 2014, стр. 516–521
Google Scholar
Дж. Бердик, Об обратной кинематике избыточных манипуляторов: характеристика многообразий самодвижения, в Международная конференция IEEE по робототехнике и автоматизации , Скоттсдейл, 1989, стр. 264–270
Google Scholar
Д. Уитни, Решено управление скоростью движения манипуляторов и человеческих протезов. IEEE транс. Человек Мах. Сист. 10 (2), 47–53 (1969)
CrossRef MathSciNet Google Scholar
- «>
Д. Ненчев, Разрешение избыточности посредством локальной оптимизации: обзор. Дж. Робот. Сист. 6 (6), 769–798 (1989)
CrossRef МАТЕМАТИКА Google Scholar
Б. Сицилиано, Кинематическое управление резервными манипуляторами роботов: учебное пособие. Дж. Интелл. Робот. Сист. 3 (3), 201–212 (1990)
CrossRef Google Scholar
Т. Йошикава, Анализ и управление роботами-манипуляторами с резервированием, Первый международный симпозиум по исследованиям в области робототехники , Питтсбург (MIT Press, Кембридж, Массачусетс, 1994), стр. 735–747
Google Scholar
К.А. Кляйн, Б.Е. Блахо, Меры ловкости для проектирования и управления кинематически избыточными манипуляторами. Междунар. Дж. Робот. Рез. 6 (2), 72–83 (1987)
CrossRef Google Scholar
- «>
К.Л. Доти, К. Мелчиорри, К. Бонивенто, Теория обобщенных инверсий в применении к робототехнике. Междунар. Дж. Робот. Рез. 12 (1), 1–19 (1993)
CrossRef Google Scholar
J. Baillieul, Избегание препятствий и устранение кинематической избыточности, в Международная конференция IEEE по робототехнике и автоматизации , 1986, стр. 1698–1704
Google Scholar
Х. Сераджи, Управление конфигурацией резервных манипуляторов: теория и реализация. IEEE транс. Робот. автомат. 5 (4), 472–490 (1989)
CrossRef Google Scholar
Дж. Пак, В. Чанг, Ю. Юм, О динамической развязке кинематически избыточных манипуляторов, в Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , 1999, стр. 1495–1500
Google Scholar
- «>
О. Канун, Ф. Ламиро, П.-Б. Вибер, Кинематическое управление избыточными манипуляторами: обобщение структуры приоритета задачи на задачу неравенства. IEEE транс. Робот. 27 (4), 785–792 (2011)
CrossRef Google Scholar
М. Лю, А. Микаэлли, П. Эврард, А. Эсканде, К. Андриот, Интерактивные виртуальные люди: двухуровневая система управления приоритетами с гаечными ограничениями. IEEE транс. Робот. 28 (6), 1309–1322 (2012)
CrossRef Google Scholar
М. Брандао, Л. Хамоне, П. Кричка, Н. Эндо, К. Хашимото, А. Таканиши, Достижение недостижимого: интеграция движения и движений всего тела для расширенного визуально управляемого достижения, в IEEE — Международная конференция РАН по роботам-гуманоидам , 2013
Google Scholar
- «>
А.Е.Альберта, Регрессия и псевдообратная реакция Мура-Пенроуза , 1-е изд. (Академик Пресс, Нью-Йорк, 1972)
МАТЕМАТИКА Google Scholar
М.С. Константинов, М.Д. Марков, Д. Ненчев, Кинематическое управление резервными манипуляторами, 11-й Международный симпозиум по промышленным роботам , Токио, 1981, стр. 561–568
Google Scholar
Х. Ханафуса, Т. Йошикава, Ю. Накамура, Анализ и управление шарнирными роботами-манипуляторами с резервированием, в Подготов. IFAC ’81 World Congress , 1981, стр. 78–83.
Google Scholar
Д. Ненчев, Ограниченные матрицы Якоби избыточных манипуляторов в задачах с ограниченным движением. Междунар. Дж. Робот. Рез. 11 (6), 584–597 (1992)
CrossRef Google Scholar
- «>
Д. Ненчев, Рекурсивная локальная кинематическая инверсия с динамическим распределением приоритетов задач, в Международная конференция IEEE по робототехнике и автоматизации , Мюнхен, 1994, стр. 2698–2703
Google Scholar
Б. Сицилиано, Ж.-Ж. Слотин, Общая структура для управления несколькими задачами в роботизированных системах с высокой избыточностью, в Fifth International Conference on Advanced Robotics (IEEE, 1991), стр. 1211–1216
. Google Scholar
Г. Антонелли, Анализ устойчивости алгоритмов обратной кинематики с обратной связью по приоритетам для резервных роботизированных систем. IEEE транс. Робот. 25 (5), 985–994 (2009)
CrossRef Google Scholar
Х. Садегян, Л. Виллани, М. Кешмири, Б. Сицилиано, Динамическое многоприоритетное управление в резервных роботизированных системах.
 Robotica 31 , 1–13 (2013)
Robotica 31 , 1–13 (2013)CrossRef Google Scholar
Л. Сентис, О. Хатиб, Синтез поведения всего тела посредством иерархического контроля поведенческих примитивов. Междунар. Дж. Робот-гуманоид. 2 (4), 505–518 (2005)
CrossRef Google Scholar
А.А. Мацеевский, С.А. Кляйн, Уклонение от препятствий для кинематически избыточных манипуляторов в динамически меняющихся средах. Междунар. Дж. Робот. Рез. 4 (3), 109–117 (1985)
CrossRef Google Scholar
Хатиб О., Обход препятствий в режиме реального времени для манипуляторов и мобильных роботов. Междунар. Дж. Робот. Рез. 5 (1), 90–98 (1986)
CrossRef Google Scholar
К.
 Гласс, Р. Колбо, Д. Лим, Х. Сераджи, Предотвращение столкновений в реальном времени для избыточных манипуляторов. IEEE транс. Робот. автомат. 11 (3), 448–457 (1995)
Гласс, Р. Колбо, Д. Лим, Х. Сераджи, Предотвращение столкновений в реальном времени для избыточных манипуляторов. IEEE транс. Робот. автомат. 11 (3), 448–457 (1995)CrossRef Google Scholar
Д. Ненчев, З. Сотиров, Динамическое распределение приоритетов задач для кинематически избыточных робототехнических механизмов, в Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , Мюнхен, 1994 г., стр. 518–524
Google Scholar
О. Брок, О. Хатиб, С. Виджи, Уклонение от препятствий и поведение в движении для мобильных манипуляций, Международная конференция IEEE по робототехнике и автоматизации , 2002 г., стр. 388–393
Google Scholar
А. Дитрих, Т. Уимбок, А. Альбу-Шаффер, Г. Хирцингер, Реактивное управление всем телом: динамическое мобильное манипулирование с использованием большого количества приводимых в действие степеней свободы.
 IEEE-робот. автомат. Маг. 19 (2), 20–33 (2012)
IEEE-робот. автомат. Маг. 19 (2), 20–33 (2012)CrossRef Google Scholar
Ф. Кейт, П.-Б. Вибер, Н. Мансард, А. Хеддар, Анализ разрывов в управлении пространством задач с приоритетами при дискретных операциях планирования задач, в Международная конференция IEEE по интеллектуальным роботам и системам , 2011 г., стр. 3887–3892
Google Scholar
Дж. Ли, Н. Мансард, Дж. Парк, Промежуточный подход к желаемому значению для перехода задачи роботов в кинематическое управление. IEEE транс. Робот. 28 (6), 1260–1277 (2012)
CrossRef Google Scholar
Т. Петрич, Л. Жлайпах, Плавный непрерывный переход между задачами на кинематическом уровне управления: предотвращение препятствий как задача управления. Робот. Автон. Сист.
 61 (9), 948–959 (2013)
61 (9), 948–959 (2013)CrossRef Google Scholar
Д. Ненчев, Ю. Цумаки, М. Учияма, Управление движением в реальном времени в окрестностях особенностей: сравнительное исследование методов SC и DLS, в Международная конференция IEEE по робототехнике и автоматизации , 1999 г. , стр. 506–511
Google Scholar
Мансард Н., Хатиб О., Хеддар А. Унифицированный подход к интеграции односторонних ограничений в стек задач. IEEE транс. Робот. 25 (3), 670–685 (2009)
CrossRef Google Scholar
Т. Петрич, А. Гамс, Й. Бабич, Л. Жлайпах, Структура контроля рефлекторной устойчивости для роботов-гуманоидов. Автон. Роботы 34 (4), 347–361 (2013)
CrossRef Google Scholar
- «>
А. Дитрих, Т. Уимбок, А. Альбу-Шаффер, Г. Хирцингер, Интеграция реактивного предотвращения самостолкновений на основе крутящего момента в иерархию задач. IEEE транс. Робот. 28 (6), 1278–1293 (2012)
CrossRef Google Scholar
H. Sugiura, M. Gienger, H. Janssen, C. Goerick, Предотвращение столкновений в реальном времени с управлением движением всего тела для роботов-гуманоидов, в IEEE/RSJ International Conference on Intelligent Robots and Systems , 2007, стр. 2053–2058
Google Scholar
О. Стассе, А. Эсканде, Н. Мансард, С. Миоссек, П. Эврар, А. Хеддар, Задача предотвращения (само)столкновения в реальном времени на гуманоидном роботе HRP-2, в Международная конференция IEEE по робототехнике и автоматизации (IEEE, 2008 г.), стр. 3200–3205
Google Scholar
- «>
Дж. Чжао, Н.И. Бадлер, Инверсная кинематика в реальном времени с ограничениями по суставам и пространственными ограничениями. Тех. Представитель Пенсильванского университета, 1989 г.
CrossRef Google Scholar
М. Де Ласа, А. Герцманн, Приоритетная оптимизация для управления пространством задач, в Международная конференция IEEE/RSJ по интеллектуальным роботам и системам , 2009 г., стр. 5755–5762
Google Scholar
Х. Изерманн, Линейная лексикографическая оптимизация. ОР Спектрум 4 (4), 223–228 (1982)
CrossRef МАТЕМАТИКА Google Scholar
DE Стюарт, Дж. К. Тринкл, Неявная пошаговая схема для динамики твердого тела с неупругими столкновениями и кулоновским трением. Междунар. Дж. Нумер. Методы инж. 39 (15), 2673–2691 (1996)
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
- «>
К. Ямане, Ю. Накамура, Численно надежный решатель LCP для моделирования сочлененных твердых тел в контакте, в Robotics: Science and Systems IV , Цюрих (MIT Press, 2008), стр. 89–104
Google Scholar
Н. Мансар, Ф. Шометт, Последовательность задач для высокоуровневого управления на основе датчиков. IEEE транс. Робот. 23 (1), 60–72 (2007)
CrossRef Google Scholar
Н. Мансард, О. Хатиб, Непрерывный закон управления от односторонних ограничений, в Международная конференция IEEE по робототехнике и автоматизации , 2008, стр. 3359–3364
Google Scholar
Н. Мансар, А. Ремазей, Ф. Шометт, Непрерывность законов управления с переменным набором признаков. IEEE транс. автомат. Контроль 54 (11), 2493–2505 (2009)
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
- «>
О. Канун, Ф. Ламиро, П.-Б. Вибер, Ф. Канехиро, Э. Йошида, Ж.-П. Ломонд, Приоритизация систем линейного равенства и неравенства: применение к локальному планированию движения для резервных роботов, в Международная конференция IEEE по робототехнике и автоматизации , 2009, стр. 2939–2944
Google Scholar
А. Эсканде, Н. Мансар, П.-Б. Вибер, Быстрое разрешение иерархической инверсной кинематики с ограничениями неравенства, IEEE International Conference on Robotics and Automation , 2010, стр. 3733–3738
Google Scholar
О. Канун, Приоритетное кинематическое управление в реальном времени при ограничениях неравенства для избыточных манипуляторов, в Robotics: Science and Systems VII , ed. Х. Даррант-Уайт, Н. Рой, П. Аббил (MIT Press, Кембридж, Массачусетс, 2012 г.), стр. 145–152
Google Scholar
- «>
Д. Монтана, Кинематика контакта и захвата. Междунар. Дж. Робот. Рез. 7 (3), 17–32 (1988)
CrossRef Google Scholar
К.Х. Хант, Структурная кинематика параллельных роботов-манипуляторов. Дж. Мех. Транс. автомат. Дес. 105 (4), 705 (1983)
Google Scholar
А. Дитрих, К. Отт, А. Альбу-Шаффер, Многоцелевой контроль соответствия резервных манипуляторов: иерархия, управление и стабильность, в Международной конференции IEEE/RSJ по интеллектуальным роботам и системам (IEEE, 2013), стр. 3043–3050
Google Scholar
Л. Сентис, Дж. Петерсен, Р. Филипсен, Реализация и анализ стабильности приоритетных контроллеров, совместимых со всем телом, на колесном роботе-гуманоиде на неровной местности. Автон. Роботы 35 (4), 301–319 (2013)
CrossRef Google Scholar
- «>
A. Rennuit, A. Micaelli, X. Merlhiot, C. Andriot, F. Guillaume, N. Chevassus, D. Chablat, P. Chedmail, Архитектура пассивного управления для виртуальных людей, в IEEE/RSJ International Conference по интеллектуальным роботам и системам , 2005 г., стр. 1432–1437
Google Scholar
К. Отт, А. Дитрих, А. Альбу-Шаффер, Приоритетный многозадачный контроль соответствия резервных манипуляторов. Автоматика 53 , 416–423 (2015)
CrossRef MathSciNet МАТЕМАТИКА Google Scholar
Б. Дариуш, Г.Б. Хаммам, Д. Орин, Ограниченное разрешенное управление ускорением для гуманоидов, в IEEE/RSJ International Conference on Intelligent Robots and Systems , 2010, стр. 710–717
Google Scholar
Г.Б. Хаммам, П.М. Венсинг, Б.
 Дариуш, Д.Э. Орин, Кинодинамически последовательное перенацеливание движения для гуманоидов. Междунар. Дж. Робот-гуманоид. 12 , 1550017 (2015)
Дариуш, Д.Э. Орин, Кинодинамически последовательное перенацеливание движения для гуманоидов. Междунар. Дж. Робот-гуманоид. 12 , 1550017 (2015)Перекрестная ссылка Google Scholar
Скачать ссылки
Кинематика — документация CoopRobo 1.0.0
Кинематика в классической механике изучает описание движения точек, тел (объектов) и групп тел без учета сил, заставляющих их двигаться . В мобильной робототехнике кинематика помогает нам понять и количественно оценить ограничения, связанные с конструкцией робота, что подразумевает ограничения в его движении. Также мы можем нарисовать пути и траектории, которые может делать робот. Здесь текст сосредоточен на колесных роботах, которые могут двигаться только в 2D-пространстве.
Pioneer P3-DX
Pioneer P3-AT
P3-DX — полноприводный, а P3-AT — полноприводный.
Компания Omron Adept MobileRobots рассматривает в своем руководстве P3-DX как робота с дифференциальным приводом, а P3-AT как робота с скользящим/скользящим приводом.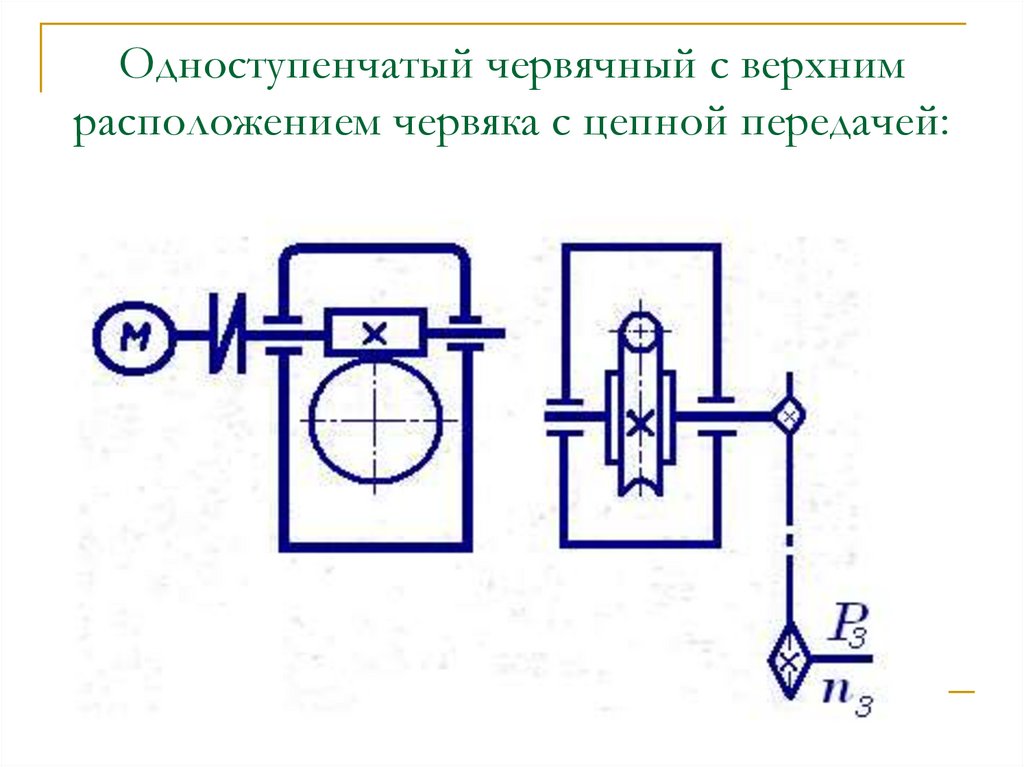 Для нашего блага оба моделируются как транспортные средства с дифференциальным приводом, потому что точный центр вращения при скользящем/скользящем приводе непредсказуем [1].
Для нашего блага оба моделируются как транспортные средства с дифференциальным приводом, потому что точный центр вращения при скользящем/скользящем приводе непредсказуем [1].
Чтобы представить движение мобильного робота, мы должны задать системы отсчета и определить их положение. Если мы рассматриваем робота как твердое тело, у него есть два основных каркаса. Это глобальная система отсчета, фиксированная в мире, и локальная система отсчета, фиксированная роботом.
Глобальная система отсчета и локальная система отсчета робота. Рисунок из [1].
На рисунке показан робот и его системы отсчета.
Где \(X_I\) и \(Y_I\) определяют глобальную систему отсчета, также известную как инерциальная система отсчета, а \(X_R\) и \(Y_R\) определяют локальную систему отсчета или систему отсчета робота.
Координаты \(x\) и \(y\) представляют положение робота в глобальной системе отсчета, точка P, тогда как \(\theta\) представляет собой угловую разницу между глобальной и локальной системами отсчета.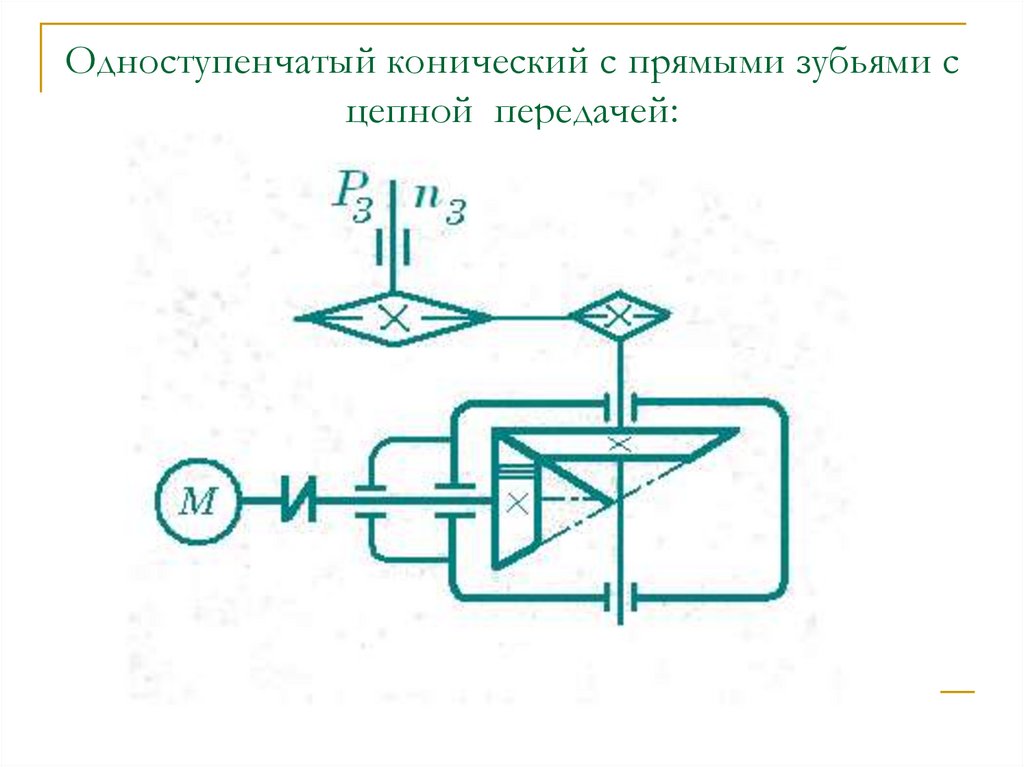 Таким образом, мы представляем позу робота в виде вектора с этими тремя компонентами. 9Т\).
Однако, поскольку робот движется под действием силы тяжести, которая удерживает его в пределах евклидовой плоскости, \(x\) и \(y\) описывают положение робота, а \(\theta\) описывают ориентацию в плоскости.
Двумерное пространство, в котором находится робот, называется C-пространством [5], впервые формализованным в [6], также называемым конфигурационным пространством.
Конфигурация — это полная спецификация положения каждой точки в системе.
Пространство всех конфигураций C-пространство .
Таким образом, мы представляем позу робота в виде вектора с этими тремя компонентами. 9Т\).
Однако, поскольку робот движется под действием силы тяжести, которая удерживает его в пределах евклидовой плоскости, \(x\) и \(y\) описывают положение робота, а \(\theta\) описывают ориентацию в плоскости.
Двумерное пространство, в котором находится робот, называется C-пространством [5], впервые формализованным в [6], также называемым конфигурационным пространством.
Конфигурация — это полная спецификация положения каждой точки в системе.
Пространство всех конфигураций C-пространство .
Теперь мы можем использовать это определение для описания элементов, представленных в локальном фрейме, в глобальном фрейме и наоборот. Например, мы можем сопоставить движение, рассчитанное в глобальной системе координат, с движением в локальной системе координат робота. Или мы можем отобразить препятствия, обнаруженные роботом, с точки зрения глобальной системы отсчета.
\[\begin{split}R(\theta) = \left[ \begin{array}{c} cos \theta & sin \theta & 0 \\
-sin \ тета & cos \ тета & 0 \\
0 & 0 & 1 \end{массив} \right]\end{split}\] 9Т\).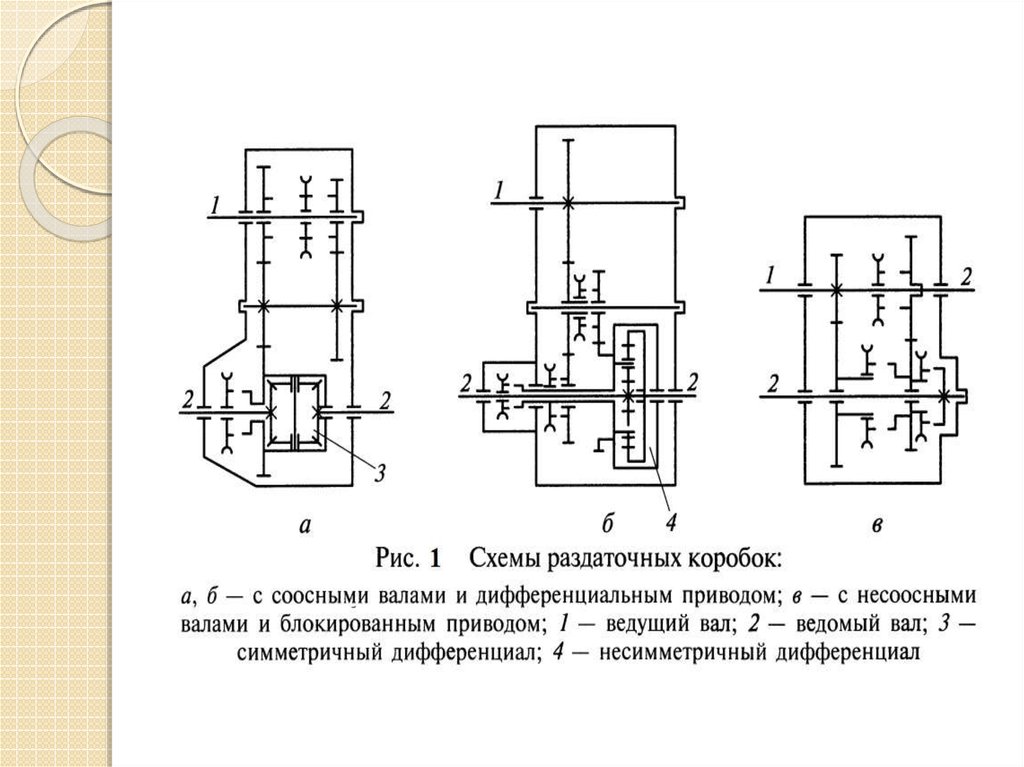 Именно поэтому связь между производной позы в кадрах.
Именно поэтому связь между производной позы в кадрах.
Колеса и связанные с ними ограничения
«Колесные мобильные роботы (WMR) представляют собой класс механических систем, характеризующихся кинематическими ограничениями, которые не являются интегрируемыми и поэтому не могут быть исключены из уравнений модели» [2]. Если мы хотим изучить и описать движение робота, мы также должны указать, каковы гипотезы и ограничения колес. Существуют три основные гипотезы о кинематической модели колесного робота во время движения; они:
- Каждое колесо остается перпендикулярным своей плоскости;
- Между плоскостью и колесом имеется только одна точка контакта;
- Есть только качение без проскальзывания;
И два ограничения:
- О качении: составляющая движения по плоскости колеса равна скорости вращения колеса;
- О скольжении: составляющая движения по ортогональному направлению равна нулю;
Некоторые авторы могут называть эти ограничения «чистым условием качения и вращения».
Модель дифференциального привода
Теперь мы углубимся в моделирование кинематики дифференциального привода. Дудек и др. говорят, что дифференциальный привод состоит из двух колес, установленных на одной оси с раздельными двигателями [3]. Каждое колесо вносит свой вклад в движение робота, поэтому для полного описания движения робота мы должны вычислить каждый вклад.
Скорости колес и рама робота.
На изображении показан робот, скорости колес и локальный кадр. \(\dot{\phi}_1\) и \(\dot{\phi}_2\) — скорость вращения левого и правого колес. \(r\) — это радиус колеса, а расстояние между двумя колесами равно \(l\). При этом \(v_1\) — скорость левого колеса по земле, а \(v_2\) — скорость правого колеса. Поскольку колеса влияют на движение робота независимо, мы можем проанализировать каждый вклад отдельно.
\[\begin{split}\begin{массив}{c} v_i = \frac{\dot{\phi}_i r}{2} \\ \omega_i = \frac{\dot{\phi}_i r}{2 l} \\ \text{где} я = \{1, 2\} \end{array}\end{split}\]
Точка \(P\) находится посередине между двумя колесами, поэтому каждое колесо обеспечивает половину линейной скорости робота в направлении \(X_R\). Каждое колесо также добавляет новую составляющую к угловой скорости робота.
\(v_1\) перемещает робота по часовой стрелке вокруг точки \(P\), а \(v_2\) перемещает его против часовой стрелки.
Вот почему они различаются по своему знаку.
И, используя уравнение, которое связывает угловую скорость диска с его линейной скоростью, мы получаем приведенные выше уравнения.
Каждое колесо также добавляет новую составляющую к угловой скорости робота.
\(v_1\) перемещает робота по часовой стрелке вокруг точки \(P\), а \(v_2\) перемещает его против часовой стрелки.
Вот почему они различаются по своему знаку.
И, используя уравнение, которое связывает угловую скорость диска с его линейной скоростью, мы получаем приведенные выше уравнения.
Используя теорему суперпозиции, мы имеем уравнения для линейной скорости в направлении \(X_R\) и угловой скорости в направлении \(Z_R\):
\[\begin{split}\begin{ массив}{с} v & = & v_1 + v_2 \\ \омега & = & -\омега_1 + \омега_2 \end{массив}\end{split}\]
В локальной системе отсчета имеем следующее кинематическое уравнение:
\[\begin{split}\dot{\xi_R} & = & \left[ \begin{array}{c} \frac{r}{2} & \frac{r}{2} \\ 0 и 0 \\ -\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right] \left[ \begin{array}{c} \dot{\phi}_1 \\ \dot {\phi}_2 \end{массив} \right]\end{split}\]
Примечание
В рамке робота нет скорости в направлении \(Y_R\). Потому что мы предполагали чистое условие качения и вращения. И все же он может достичь любой точки в глобальной системе отсчета.
Потому что мы предполагали чистое условие качения и вращения. И все же он может достичь любой точки в глобальной системе отсчета.
Прямая кинематика
Задача прямой кинематики пытается решить проблему, когда у нас есть управляющие входы, и мы должны знать, куда движется робот в глобальной системе отсчета. Как мы видели, чтобы решить этот вопрос, мы должны знать пять параметров робота — два параметра о геометрии робота, \(l\) и \(r\), текущая ориентация робота, \(\theta\), и, по крайней мере, два входа, \(\dot{\phi}_1\) и \(\dot{\phi}_2\).
\[\begin{split}\dot{\xi_I} = \left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{ array} \right] = f(l, r, \theta, \dot{\phi_1}, \dot{\phi_2})\end{split}\]
\(f\) — это функция, которая решает прямую проблема с кинематикой.
Сопоставить вектор параметров \(\{l, r, \theta, \phi_1, \phi_2\}\) и состояние робота в инерциальной системе отсчета.
Мы должны использовать матрицу, связывающую скорость вращения и производную состояния робота в локальной системе отсчета.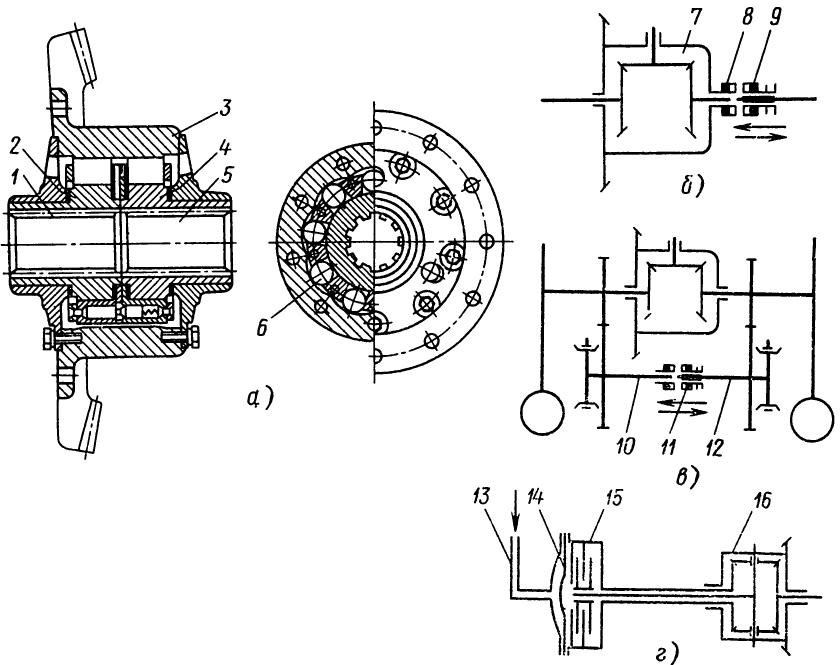 Затем мы можем преобразовать скорости робота в локальной системе координат в глобальную систему координат, используя обратную матрицу вращения. 9{-1}
\left[ \begin{array}{c} \frac{r}{2} & \frac{r}{2} \\
0 и 0 \\
-\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right]
\left[ \begin{array}{c} \dot{\phi}_1 \\ \dot{\phi}_2 \end{array} \right]\end{split}\]
Затем мы можем преобразовать скорости робота в локальной системе координат в глобальную систему координат, используя обратную матрицу вращения. 9{-1}
\left[ \begin{array}{c} \frac{r}{2} & \frac{r}{2} \\
0 и 0 \\
-\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right]
\left[ \begin{array}{c} \dot{\phi}_1 \\ \dot{\phi}_2 \end{array} \right]\end{split}\]
Затем
\[ \begin{split}f(l, r, \theta, \dot{\phi_1}, \dot{\phi_2}) & = & \left[ \begin{array}{c} потому что \тета &-sin \тета & 0 \\ грех \ тета & cos \ тета & 0 \\ 0 и 0 и 1 \end{массив} \right] \left[ \begin{array}{c} \frac{r}{2} & \frac{r}{2} \\ 0 и 0 \\ -\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right] \left[ \begin{array}{c} \dot{\phi}_1 \\ \dot{\phi}_2 \end{массив} \right]\end{split}\]
\[\begin{split}f(l, r, \theta, \dot{\phi_1}, \dot{\phi_2}) & = & \left[ \begin{array}{c} \frac{r cos \theta}{2} & \frac{r cos \theta}{2} \\ \frac{r sin \theta}{2} & \frac{r sin \theta}{2} \\ -\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right] \left[ \begin{array}{c} \dot{\phi}_1 \\ \dot{\phi}_2 \end{array} \right]\end{split}\]
Или
\[\ begin{split}\dot{\xi_I} & = & \left[ \begin{array}{c} \frac{r cos \theta}{2} & \frac{r cos \theta}{2} \\ \frac{r sin \theta}{2} & \frac{r sin \theta}{2} \\ -\frac{r}{2 l} & \frac{r}{2 l} \end{array} \right] \left[ \begin{array}{c} \dot{\phi}_1 \\ \dot{\phi}_2 \end{массив} \right]\end{split}\] 9{t} (\dot{\phi_2}(t) — \dot{\phi_1}(t)) dt \end{cases}\end{split}\]
Обратная кинематика
Задача обратной кинематики противоположна прямой задаче.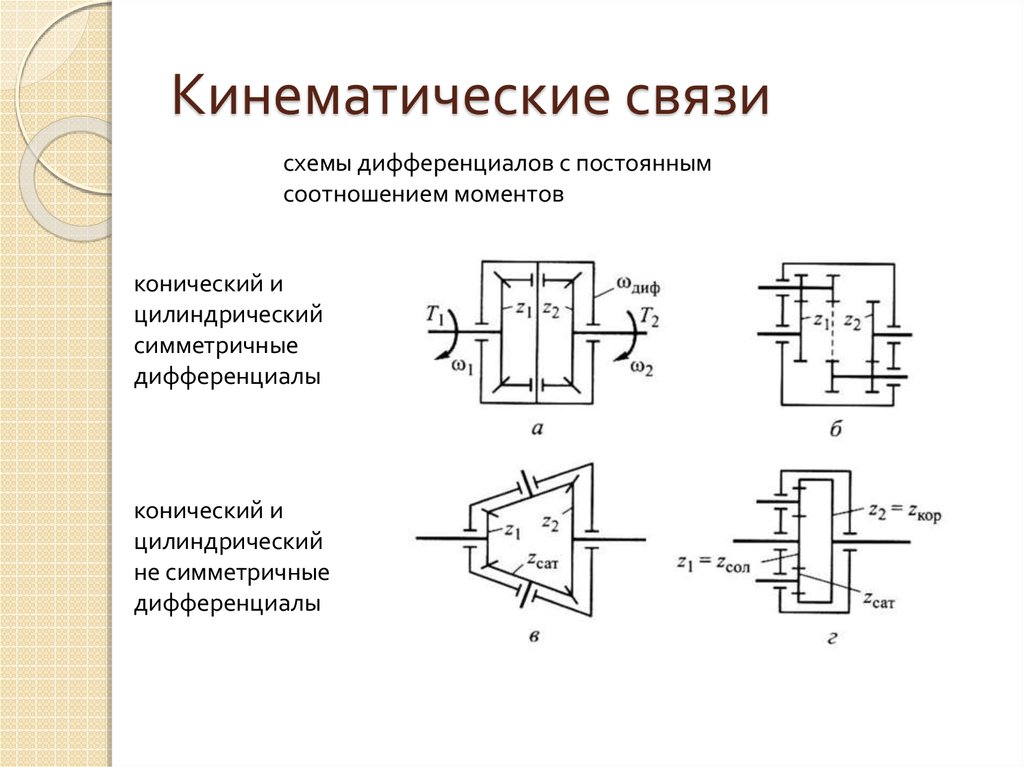 Задача направлена на решение следующего вопроса: «Учитывая желаемую позу, какие элементы управления необходимы для достижения желаемой позы?».
Мы уже знаем связь между скоростью и
Задача направлена на решение следующего вопроса: «Учитывая желаемую позу, какие элементы управления необходимы для достижения желаемой позы?».
Мы уже знаем связь между скоростью и
\[\begin{split}\left[ \begin{array}{c} \dot{\phi_1} \\ \dot{\phi_2}\end{array} \right ] = г (\ точка {\ xi_I}) \ конец {разделить} \] 9{-1}\end{split}\]
Как видим, матрица, представляющая функцию \(f\), необратима. Прямая кинематика — простая задача, потому что у нас есть одно и только одно решение. Тем не менее инверсная кинематика часто не поддается аналитическому решению; обычно у нас есть более одного решения или ни одного. Однако мы можем попытаться решить проблему, ограничив возможные решения, такие как \(\dot{\phi}_1 = \dot{\phi}_2\) или \(\dot{\phi}_1 = -\dot{\ фи}_2\).
Прямая линия
Если мы ограничим решение \(\dot{\phi}_1 = \dot{\phi}_2 = \dot{\phi}\), где \(\dot{\phi} > 0\), робот должен двигаться по прямой. Тогда движение робота упрощается до:
\[\begin{split}\xi_I = \left[ \begin{array}{c} x’ \\ y’ \\ \theta’ \end{array} \right] «=» \left[ \begin{array}{c} x + v cos (\theta) \delta t \\ y + v sin (\theta) \delta t \\ \theta \end{array} \right]\end{ split}\]
Вращение на месте
Аналогично, если мы ограничим решение \(-\dot{\phi}_1 = \dot{\phi}_2\), с \(\dot{\phi}_2 > 0\), робот должен вращаться вокруг точки P.
\[\begin{split}\xi_I = \left[ \begin{array}{c} x’ \\ y’ \\ \theta’ \end{массив} \right] = \left[ \begin{array}{c} x \\ y \\ \theta + \frac{2 v}{l} \delta t \end{array} \right]\end{split}\]
Движение Композиция
Если мы хотим перевести робота из любой позы в какую-то другую позу в глобальной системе отсчета, мы можем разложить движение на два вращения на месте и одно перемещение по прямой. Робот может повернуться на месте, выровняв свою ориентацию, нацелившись на целевое положение, \((x_d,y_d)\), затем двигаться вперед к целевому положению, а затем снова повернуться на месте, чтобы достичь целевого положения, \(\theta_d \). 9Т\).
Модель одноколесного велосипеда
До сих пор мы видели кинематику двухколесного робота.
Но сейчас мы поговорим о более общей и простой модели.
Предыдущая модель рассказывает нам, как робот с двумя колесами может принять определенную позу в мире, действуя на скорости колес.
Но нас не волнует, как крутится колесо; мы заботимся о позе робота.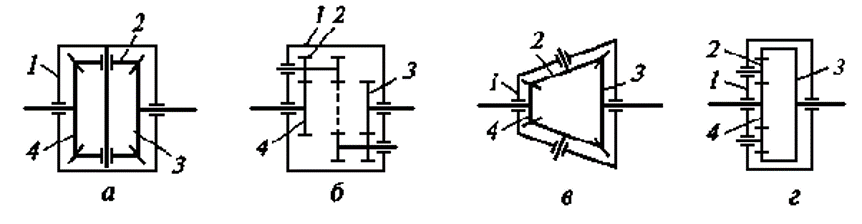 Модель моноколеса представляет собой робота только с одним колесом.
Если колесо соответствует нашему чистому условию вращения и качения, колесо имеет два управляющих входа: линейную скорость \(v\) по оси \(X_R\) и угловую скорость \(\omega\) вокруг \(Z_R\).
Итак, кинематика одноколесного робота, описываемая в инерциальной системе отсчета \(\{ X_I , Y_I , θ \}\) задается равенством
Модель моноколеса представляет собой робота только с одним колесом.
Если колесо соответствует нашему чистому условию вращения и качения, колесо имеет два управляющих входа: линейную скорость \(v\) по оси \(X_R\) и угловую скорость \(\omega\) вокруг \(Z_R\).
Итак, кинематика одноколесного робота, описываемая в инерциальной системе отсчета \(\{ X_I , Y_I , θ \}\) задается равенством
\[\begin{split}\left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array} \right] & = & \left[ \begin{array}{c} v \cos \theta \\ v \sin \theta \\ \omega \end{array} \right] & = & \left[ \begin{array}{c} \cos \theta & 0 \\ \sin \theta & 0 \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c} v \\ \omega \end{array} \right]\end{split}\]
Где \(x\), \(y\) и \(\theta\) — координаты робота в глобальной системе координат \(u = (v, \omega)\) — вектор управления.
Робот с дифференциальным приводом в глобальной системе отсчета. Рисунок из [1].
Коммерческие роботы обычно имеют интерфейс для преобразования желаемого управляющего сигнала одноколесного велосипеда в желаемую скорость вращения колеса. И специальный микроконтроллер более низкого уровня, предназначенный для управления скоростью вращения колеса.
И специальный микроконтроллер более низкого уровня, предназначенный для управления скоростью вращения колеса.
Заметки об управлении
Итак, мы должны быть в состоянии построить систему или программное обеспечение, способное, используя показанную математику, перемещать робота к любой достижимой цели. Теория управления — это раздел математики, посвященный этой проблеме. Система управления отправляет входные данные в систему и приводит переменные системы к желаемой цели. Наша система представляет собой мобильный робот. И, используя предыдущие уравнения, входные данные — это скорость вращения каждого колеса, а выходные данные — поза робота.
Контроллер должен предоставить системе входные данные, необходимые для выполнения желаемого действия. Как на изображении ниже:
Если мы видим контроллер и робота как единую систему, у нас может быть другая система с желаемым состоянием на входе и состоянием робота на выходе.
Затем мы можем создать новый контроллер, который занимается выбором желаемого состояния. Точно так же, если мы хотим контролировать скорость робота, а не только его позу, мы должны иметь возможность контролировать то, как робот движется.
Мы можем добавить скорости к вектору состояния робота и управлять ими с помощью соответствующих уравнений.
Точно так же, если мы хотим контролировать скорость робота, а не только его позу, мы должны иметь возможность контролировать то, как робот движется.
Мы можем добавить скорости к вектору состояния робота и управлять ими с помощью соответствующих уравнений.
Примечание
Робот с дифференциальным приводом имеет серьезную проблему, которая… Фэн и др. [4] в 1993 году разрабатывает контроллер движения, который…
| [1] | (1, 2, 3) Роланд Зигварт и Иллах Р. Нурбахш . 2004. Введение в автономных мобильных роботов. Компания Брэдфорд, США. |
| [2] |
|
| [3] | Грегори Дудек и Майкл Дженкин. 2010. Вычислительные принципы мобильной робототехники (2-е изд.). Издательство Кембриджского университета, США. |
| [4] |
|
| [5] | (1, 2)
 |

 по робототехнике и автоматизации, вып. 12, нет. 1, стр. 47-62, 19 фев.96.
по робототехнике и автоматизации, вып. 12, нет. 1, стр. 47-62, 19 фев.96.