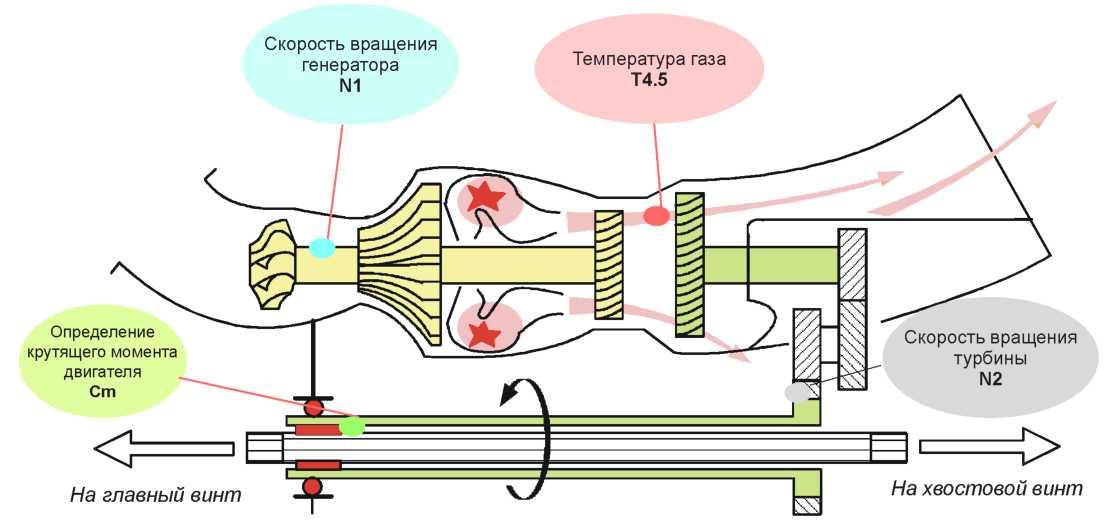
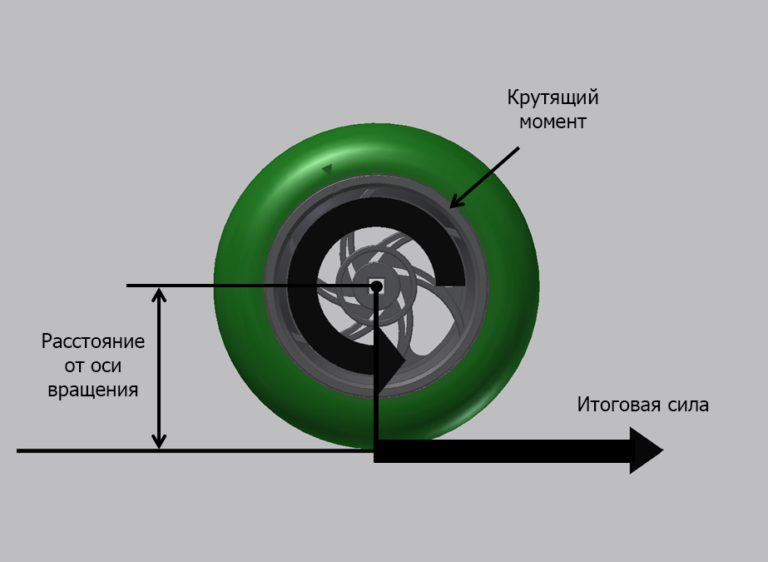
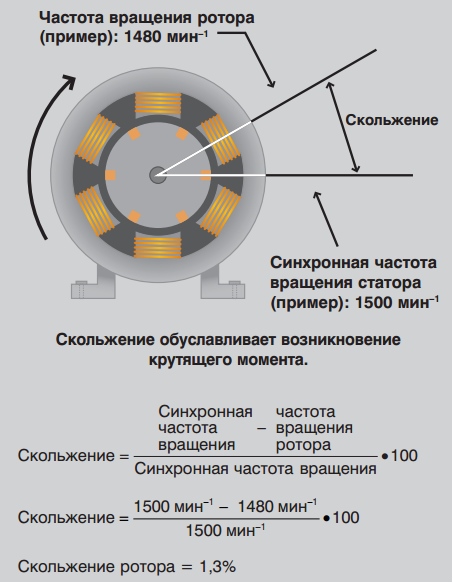
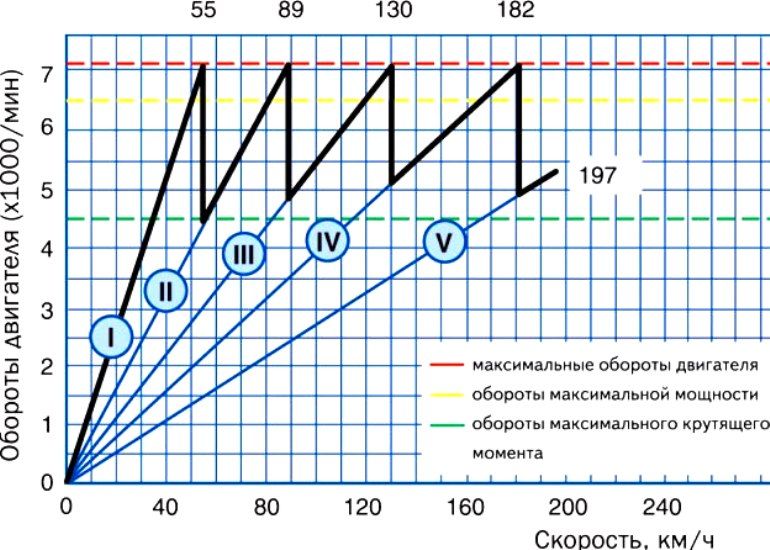
Крутящий момент, тяга и мощность

Calculate Torque

Work Piece Material: 1.1 Low Carbon Steel; Long Chip (60&#44000 PSI / 125 HBN)1.2 Low Carbon Steel; Short Chip (60&#44000 PSI / 125 HBN)2.1 Unalloyed Carbon Steel; Long Chip (95&#44000 PSI / 190 HBN)2.2 Unalloyed Carbon Steel; Short Chip (95&#44000 PSI / 190 HBN)3 Unalloyed Carbon Steel (125&#44000 PSI / 250 HBN)4 Unalloyed Carbon Steel (140&#44000 PSI / 270 HBN)5 Unalloyed Carbon Steel (150&#44000 PSI / 300 HBN)6 Low Alloyed Steel (88&#44000 PSI / 180 HBN)7 Low Alloyed Steel (135&#44000 PSI / 275 HBN)8 Low Alloyed Steel (150&#44000 PSI / 300 HBN)9 Low Alloyed Steel (175&#44000 PSI / 350 HBN)10 High Alloyed Steel (100000 PSI / 200 HBN)14.2 Stainless Steel; Aust./Fer (130&#44000 PSI / 260 HBN)15 Gray Cast Iron (180HBN)16 Gray Cast Iron (260HBN)18 Ductile(Nodular) Cast Iron (250HBN)22 Aerospace Aluminum; Heat Treated (100HBN)23 Automotive Aluminum; Si < 12%(75HBN)25 Automotive Aluminum; Si > 12% (130HBN)32 High Temperature Alloys; Fe Based (230HBN)33 High Temperature Alloys; Ni Or Co Based (250HBN)34 High Temperature Alloys; Ni Or Co Based (350HBN37 Titanium (60&#44000 PSI)41 Unalloyed Carbon Steel (140&#44000 PSI / 270 HBN)

D_m Drill diameter: in. mm

V_c Cutting speed: sfm m/min

a_p Depth of hole: in. mm

f_n Feed: in./rev mm/rev

Select Drilling Option: Drill FixHTS & HTS-CSE-Drill & KSEM

 

n Spindle speed: rpm 1/min

Q_z Metal removal rate: lnch

3/min cm³/min

V_f Unit per minute: ipm mm/min

T_c Time in cut: sec.

Your Results

M_c / M_d Torque: in-lb. Nm

F_f Thrust (Feed Force): lb-force N

P_c Power: horsepower kilowatt

Calculated Required Power

1m= 3. 2808 feet

1N= 0.22481 lb-force

1Nm= 0.737561 ft-lbs

1kW= 1.341022 hp

1 foot= 0.3048037 m

1 lb-force= 4.4482007 N

1 ft-lbs= 1.3558201 Nm

ЧТО ЗНАЧИТ КРУТЯЩИЙ МОМЕНТ? | DEWALT

Аккумуляторные инструменты. за последние десятилетия сделали мощный рывок в своем развитии. Новые технологии позволяют заменить сетевые инструменты аккумуляторными без уменьшения мощности и производительности. Возможно, вам захочется узнать как можно оценить производительность инструмента, чтобы правильно подобрать его для требуемой задачи.

Взгляд на производительность под другим углом
Залогом эффективного сверления (или закручивания) является приложение требуемого крутящего момент на максимальной скорости. Распространенным заблуждением является утверждение, что чем выше значение крутящего момента, тем быстрее мы сможем просверлить отверстие или закрутить крепеж. Это не всегда так. 

Крутящий момент – это сила, которую создает шуруповерт или дрель, чтобы повернуть объект (это может быть сверло или бит), а не скорость, с которой сверло (бит) повернется. В последние годы производители электроинструмента неуклонно увеличивают величину крутящего момента у своих изделий, хотя пользователю требует меньше величина крутящего момента для выполнения своих задач. В этой статье мы предлагаем определить зависимость производительности дрели-шуруповерта от скорости и крутящего момента.

Определения

• Мощность может быть определена по способности устройства выполнять заданную работу.
• Мощность измеряется по формуле: Скорость х Крутящий момент /K
• K – константа и варьируется в зависимости от единиц измерения крутящего момента
• Скорость — это величина оборотов дрели/шуруповерта (об/мин)
• Крутящий момент – это сила, которую создает дрель/шуруповерт для поворота сверла или биты
• Можность – это косвенный показатель объема выполненной работы за определенный период времени

 

Традиционный метод измерения крутящего момента: T

• Установка дрели/шуруповерта в стойку сверления
• Фиксация шпинделя с помощью зафиксированного в патроне стержня, жестко установленного на опоре
• Аккумулятор дрели/шуруповерта полностью заряжен
• Постепенное возрастание нагрузки Измерение скорости сверления и крутящего момента в нескольких точках

 

Новый метод измерения мощности:

• Установка дрели/шуруповерта в стойку сверления
• Фиксация шпинделя с помощью зафиксированного в патроне стержня, жестко установленного на опоре
• Аккумулятор дрели/шуруповерта полностью заряжен
• Постепенное возрастание нагрузки
• Измерение скорости сверления и крутящего момента в нескольких точках

 

Определение мощности
Номинальная расчетная мощность дрели/шуруповерта будет использоваться как эталонное значение при разработки новой модели.

Это способ оценки уровня производительности дрели/шуруповерта и является прямым следствием того, насколько быстро шуруповерт завершит работу.

Сила мощности дрели/шуруповерта измеряется с помощью номинальной мощности сверла (Units Watts Out (UWO), в той точке на графике, где скорость и крутящий момент являются самыми высокими. Чем выше UWO, тем быстрее шуруповерт будет выполняться свою работу.

Запомнить:
Крутящий момент ≠ времени требуемого для завершения работы = Выходная мощность и крутящий момент при нагрузке Макс. Мощность ватт (MWO) = Мощность двигателя в единицах измерения Watts Out (UWO) = Общая мощность дрели/шуруповерта

Эта статья взята из июльского выпуска информационного бюллетеня Грейнджера «О работе».

Как определить крутящий момент в балке

При расчете сборных или монолитных железобетонных балок (ригелей) всегда нужно внимательно относиться к крутящему моменту. Очень часто расчет на кручение требует увеличить сечение или армирование балки.

Сечение балки при кручении эффективней увеличивать в ширину (увеличение балки по высоте дает малый эффект), оптимально при кручении уходить от прямоугольного сечения к квадратному.

В каких ситуациях в балке возникает крутящий момент?

1) Если на балку опирается перекрытие только с одной стороны – оно своим весом пытается крутить балку в сторону пролета перекрытия.

2) Если на балку опирается перекрытие с двух сторон, но пролет этих перекрытий разный – тогда нагрузка от перекрытия с большим пролетом перевешивает в свою сторону и крутит балку.

3) Если на балку опирается перекрытие равных пролетов, но нагрузки на этих перекрытиях отличаются (разное назначение помещений, наличие оборудования на перекрытии и т.п.) – тогда балка также прокручивается в сторону большей нагрузки.

4) Если вдоль балки действует вертикальная нагрузка (например, от веса перегородки), сбитая в сторону от оси балки.

Рассмотрим определение крутящего момента на примерах.

Пример 1. Монолитное балочное перекрытие. Необходимо определить крутящий момент в крайней балке. Суммарная нагрузка от веса монолитного перекрытия и всех нагрузок на нем равна: qн = 675 кг/м² (нормативная) и qр =775 кг/м² (расчетная).

Расчет ведется на 1 погонный метр балки.

В монолитном перекрытии связь перекрытия с балками жесткая. При такой схеме расчетный пролет перекрытия равен пролету плиты в свету между балками L₀ = 2,8 м, а нагрузка от плиты на балку передается в месте примыкания балки к перекрытию.

Найдем нагрузку на 1 п.м балки от половины пролета плиты 2,8/2 = 1,4 м:

Рн = 675∙1,4 = 945 кг/м;

Рр = 775∙1,4 = 1085 кг/м.

Крутящий момент в балке рассчитывается умножением вертикальной нагрузки на эксцентриситет – расстояние от оси приложения этой нагрузки до оси, проходящей через центр тяжести балки. В нашем случае эксцентриситет равен половине ширины балки, т.е. 100 мм = 0,1 м.

Итак, определяем крутящий момент в балке (на 1 п.м балки):

Мн = 945∙0,1 = 94,5 кг∙м/м;

Мр = 1085∙0,1 = 108,5 кг∙м/м.

Пример 2. Сборное перекрытие опирается на балку с двух сторон. С одной стороны пролет перекрытия 6 м и есть пригруз в виде перегородки, опирающейся параллельно балке; с другой стороны пролет перекрытия 3,6 м. Нагрузка от перегородки  0,65 т/м, расстояние от оси балки до перегородки 1,5 м. Нагрузка от собственного веса перекрытия 0,3 т/м². Нагрузка на перекрытии: постоянная 0,1 т/м²; временная 0,3 т/м². Ширина балки 0,3 м. Глубина опирания плит перекрытия на балку 0,14 м.

Расчет ведется на 1 п.м балки.

Определим расчетный пролет каждого перекрытия и найдем точку приложения нагрузки от перекрытия на балку.

Плита опирается на балку на 140 мм. Нагрузка от плиты на этой площади распределена не равномерно, а по треугольнику. Максимально плита давит со стороны пролета (с края балки), а к краю плиты нагрузка сходит к нулю. Чтобы привести эту распределенную нагрузку к сосредоточенной, нужно принять ось приложения этой сосредоточенной нагрузки – в центре тяжести треугольника, на расстоянии 1/3 от края балки. У нас получается, что расстояние от края балки до сосредоточенной нагрузки 140/3 = 47 мм, а расстояние от этой нагрузки до оси, проходящей через центр тяжести балки 150 – 47 = 103 мм. Расстояние между сосредоточенными нагрузками равно расчетному пролету плиты L₀, который для наших плит будет равен:

— для плиты 6 м: L₀ = 6000 – 2∙103 = 5794 мм;

— для плиты 3,6 м: L₀ = 3600 – 2∙103 = 3394 мм.

Построим эпюры поперечных сил для наших плит.

Равномерно-распределенная нагрузка на 1 погонный метр плиты равна:

— нормативная qн = 1∙(0,3 + 0,1 + 0,3) = 0,7 т/м;

— расчетная qр = 1∙(1,1∙0,3 + 1,1∙0,1 + 1,2∙0,3) = 0,8 т/м.

Сосредоточенная нагрузка от перегородки на плите Nн = 0,65 т/м (нормативная) и Nр = 1,1∙0,65 = 0,72 т/м (расчетная) находится на расстоянии 1500 мм от оси балки и на расстоянии 1500 – 103 = 1397 мм от принятой нами точки опоры плиты, через которую проходит ось передачи вертикальной нагрузки на балку.

Схема для нормативных нагрузок будет следующая (так как плиты опираются шарнирно, то каждую из них нужно посчитать по отдельной схеме):

Левая плита разбита на два участка: 1-2 и 2-3, правая плита представляет собой один участок 4-5.

В правой плите мы сразу можем найти значения поперечной силы:

Q = 0,5∙qL₀ = 0,5∙0,65∙3,394 = 1,1 т.

Построим эпюру для правой плиты:

Значение поперечной силы на опоре (в точке 4) равно искомой нагрузке, которую плита передает на балку: Р₄= 1,1 т (направлена вниз).

Теперь разберемся с эпюрой для левой плиты. Так как помимо распределенной нагрузки у нас есть сосредоточенная сила, у нас будет несколько больше операций.

Для удобства расчета левой плиты заменим равномерно распределенную нагрузку q равнодействующей силой N:

N_1-2 = 0.65∙4,397 = 2,86 т;

N_2-3 = 0,65∙1,397 = 0,91 т.

Зная, что в шарнирно-опирающейся плите моменты на опоре равны нулю, составим уравнение равновесия, чтобы найти реакции на опоре.

ΣМ₁ = 0:

2,86∙2,199 + 0,65∙4,397 + 0,91∙5,096 – R₃∙5,794 = 0, откуда найдем реакцию:

R₃ = -13.78/5,794 = 2,38 т.

ΣМ₃ = 0:

0,91∙0,698 + 0,65∙1,397 + 2,86∙3,595 – R₁∙5,794 = 0, откуда найдем реакцию:

R₁ = 11,82/5,794 = 2,04 т.

Строить эпюру поперечных сил в плите для определения крутящего момента в балке нам не нужно, т.к. найденная нами реакция на опоре R₃ равна максимальной поперечной силе и равна нагрузке, передаваемой плитой на балку: Р₃= 2,38 т (направлена вниз).

Теперь у нас есть все исходные данные для определения крутящего момента.

Определим нормативный крутящий момент путем умножения сил на плечо. Принимаем силу, вращающую балку против часовой стрелки со знаком «+», а по часовой – со знаком «-«:

Мн = 2,38∙0,103 – 1,1∙0,103 = 0,13 т∙м/м – нормативный крутящий момент, приходящийся на 1 п. м балки.

Расчетный крутящий момент находится точно так же.

Пример 3. Вдоль балки расположена перегородка, которая сбита относительно оси балки на 150 мм. Перекрытие опирается на балку с двух сторон, пролеты перекрытия и нагрузки – одинаковые. Толщина перегородки 0,12 м, материал кирпич (1,8 т/м³), высота 3 м.

Расчет ведем на 1 погонный метр балки.

Определим вертикальную нагрузку от перегородки:

0,12∙3∙1,8 = 0,65 т/м – нормативная нагрузка;

1,1∙0,65 = 0,72 т/м – расчетная нагрузка.

Определим крутящий момент в балке путем умножения силы на плечо:

Мн = 0,65∙0,15 = 0,1 т∙м/м;

Мр = 0,72∙0,15 = 0,11 т∙м/м.

class=»eliadunit»> Добавить комментарий

Расчет параметров двигателей колесного робота

Как выбрать подходящие двигатели для колесного робота? Ответить точно на этот вопрос в начале конструирования робота непросто. Для этого нужно знать вес робота, а он еще не построен. Однако, технические характеристики и размеры двигателей значительно влияют на окончательные параметры мобильного робота. Для того, чтобы получить полную информацию, необходимо учесть вращающий момент, скорость и мощность. Для колесного робота также необходимо подобрать диаметр колес и определить правильное передаточное число зубчатой передачи для расчета скорости его движения.

 

Крутящий момент

Крутящий момент двигателя  — это сила, с которой он воздействует на вращаемую ось. Для того, чтобы робот мог двигаться, необходимо, чтобы эта сила превышала вес робота (выражаемый в Н/м).

Некоторые употребляют вместо понятия крутящий момент, термин вращающий момент. По сути это одно и то же. И то и другое являются моментами, просто в технике крутящий момент — это нагрузка на колесе, а вращающий момент — нагрузка в технической науке под названием «Сопротивление материалов». 

Рассмотрим сильно упрощенную идеализированную модель колесного робота.

Упрощенная модель колесного робота

В нашем случае, вес робота равен 1кг, и мы хотим добиться максимальной скорости его движения 1м/с при радиусе колеса равном 20мм.

При движении по прямой на расстояние 1м, рассчитаем ускорение, необходимое для достижения скорости в 1м/с.

   

где  — расстояние, пройденное роботом,  — его начальная скорость (стартуем с места, поэтому ),

   

где  — скорость робота, -его  ускорение.

Подставим значения, принятые в нашей модели, получим

 м/с²

Вращающий момент, который необходим для перемещения робота и получения им ускорения, необходимого для достижения максимальной скорости рассчитывается следующим образом:

   

При  — момент инерции и  — угловое ускорение, получим

   

Здесь м/с² — ускорение свободного падения (округлим его до 10),  — радиус колеса,  — масса всего робота

Подставив значения, получим

мН·м

Для перевода величины, выраженной в Н·м в кг·см нужно учесть, что 1Н = 0. 102 кг и 1м = 100 см. Поэтому 50 мН·м = 50 · 0.102 : 1000 * 100 = 0.51 кг · см.

Полученный крутящий момент распределяется между двумя двигателями робота и его еще нужно поделить на передаточное число используемой зубчатой передачи (подробнее про зубчатые передачи можно почитать здесь).

 

Мощность

Для расчета максимальной мощности двигателей нам понадобится частота вращения, которая выражается в оборотах в минуту

(об/мин) =

или в радианах в секунду

(рад/с) =

через круговую частоту

Подставив радиус колеса, получим

рад/с

или

об/мин.

Мощность двигателей пропорциональна крутящему моменту и частоте вращения:

   

Подставив сюда формулы для крутящего момента и частоты, получим:

   

Используя собственные значения, получим

Вт

Опять же, мы получили суммарную мощность для всех двигателей, в нашем случае двигателя два, поэтому необходимо разделить результат на два и, как и в случае с расчетом крутящего момента, если используются зубчатые передачи, разделить на передаточное число зубчатых передач.

Обратите внимание, что мы рассчитали механическую мощность вырабатываемую двигателями, а не электрическую мощность, которую они потребляют. Необходимо учитывать КПД двигателей, который будет отличаться в зависимости от модели двигателя. Выбирать нужно двигатели, естественно, с бóльшим КПД.

Для обеспечения оптимальных характеристик лучше использовать двигатели с запасом по мощности, как минимум в два раза.

Для нашего примера двухколесного робота, с использованием передаточного числа равного 10,  характеристики устанавливаемых двигателей должны быть следующими:

• частота вращения — 477 · 10 ≈ 5000$ об/мин
• вращающий момент — 50 мН·м/10 = 5 мН·м
• электрическая мощность — 5 Вт (я взял КПД равный 90%)

 

---

Еще по этой теме

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

Внутренний крутящий момент — Porsche Kazakhstan

Альпинист Томас Бубендорфер успешно использует философию Porsche Intelligent Performance в своей профессии: поступать умно в предлагаемых обстоятельствах.

Походы Томаса Бубендорфера, один ли он или в составе группы, всегда заканчиваются самоанализом. Вот и сейчас, высоко над Лазурным берегом и бухтой у мыса Ферра, все то же самое. Мы идем по следам Фридриха Ницше, который ходил в Эз, чтобы писать там «Так говорил Заратустра», свою «Книгу для всех и ни для кого». Мы взбираемся по крутой, каменистой тропе. Macan был бы здесь в самый раз. Но он остался внизу, в Монте-Карло, чтобы сверкать и привлекать внимание. Здесь, в вышине, из скал растут сосны, и нельзя сбиваться с размеренного шага. Для альпиниста Бубендорфера, который, будучи самым молодым в своей профессиональной касте, в одиночку лазал по альпийским скалам, этот поход не более, чем разминка. Казалось бы. Выглядит он отлично, несмотря на свои 52 года. Физически вполне силен. Но он относится к этому путешествию отнюдь не беззаботно. И дело не в скорости и не в степени трудности маршрута. Дело в движении, как это и завещал Ницше: «Иди своим путем». Австриец Бубендорфер вдруг останавливается на крутом повороте тропы и, оборачиваясь к спутникам, произносит: «Правильный темп каждый должен определить для себя сам». И рассказывает о менеджерах, которые, присев здесь, неожиданно почувствовали то, что никогда раньше не ощущали: «Это было ощущение того, что дарило им благодать».

Коронный номер австрийского скалолаза — восхождение по замерзшим водопадам, как здесь в Конье, долине Аоста

Поспевать за спортсменом-экстремалом довольно трудное дело — и для тела, и для головы

Томас Бубендорфер своего рода инженер человеческих эмоций. И не случайно он давно ездит на Porsche, как не случайно и то, что он выступает в музее Porsche и перед менеджерами компании. С горных вершин мира он принес с собой гораздо больше, чем только сногсшибательные фотографии. Свой опыт, стратегию и результаты исследований он сконцентрировал в программе, которую назвал Intelligent Peak Performer, где «пик» — это вершина. Разработанные им приемы умного развития человеческого потенциала для высоких достижений при одновременном бережном обращении с внутренними ресурсами обнаруживают поразительные параллели со стратегией достижения эффективности и мощности производителя спортивных автомобилей, получившей название Porsche Intelligent Performance. У Porsche она означает разработку общей концепции, в которой гармонично и хитроумно сочетаются динамика и эффективность, мощность и безопасность, спортивность и универсальность использования. Бубендорфер: «Porsche отвечает за внешний аспект водителя, я — за внутренний».

Тот, кто думает, что сейчас начнется милая беседа поклонников спортивных автомобилей, будет разочарован. Скорее даже ошеломлен. «Многие люди лучше знают свой автомобиль, нежели свой организм». Это, конечно, провокация, но провокация сознательная. Томас Бубендорфер знает, что такое экстремальные ситуации, и не только что касается гор. Ему знакомы высокие требования и вызовы, с которыми сталкивается современный человек. Подобно тому, как инженеры Porsche используют опыт автоспорта в моделях для обычных дорог, скалолаз переносит свои сложившиеся в горах взгляды на будничную жизнь. Силы у человека может быть достаточно, разъясняет он, ее только надо использовать в нужное время и прилагать в нужном месте. Высвободившийся потенциал автоматически повысит качество жизни. Взяв ответственность за себя, человек, в конечном счете, обретает также веру в себя. Во многом это вопрос равновесия. Мы продолжаем наш путь, а Бубендорфер формулирует: «Поступать умно в предлагаемых обстоятельствах».

Свой внутренний путь нашел в Приморских Альпах также философ — и отобразил сие в своем произведении «Так говорил Заратустра»

Этому человеку, чьи жизнь и везение порой висели на двух или трех пальцах, ведомы и сомнения, и отчаяние. Он ценит это невероятное чувство свободы — оставаться в одиночестве. Согласно его учению, способность принимать для себя правильные решения, во многом связано с внутренним чувством готовности. Внутренним крутящим моментом, говоря автомобильным языком. И притом «умным» моментом. Сочетание спорта и философии, которое отображено во многих его книгах, берет свое начало в одном очень давнем случае. Томасу тогда было 15, он ежедневно по 300 раз подтягивался на перекладине, мог пробежать 40 километров. Однажды его дед, стоя на пороге, спросил: «А что ты сделал для своей головы?» Томас ответил, что с утра был на уроках в гимназии, но дед не отступал: «Ты занимаешься спортом больше, чем другие. Но тогда ты и духовно должен больше развиваться». И Томас взял за правило читать по 100 страниц в день: он хотел отныне быть всегда готовым дать достойный ответ на вопрос деда.

Томас Бубендорфер считает, что правильное сознание часто должно быть прежде разбужено, чтобы произвести правильное действие. Держать себя и быть в форме, как автомобиль — снижать расход топлива, при этом постоянно повышая эффективность — вот его миссия. Понятие «баланс между трудовой и личной жизнью» может показаться кому-то данью моде, поэтому Томас сразу предупреждает: «Я не гуру». И не избавлен от ошибок, добавляет он. «У каждого человека есть слабые места, и он должен это разумно учитывать. Не надо слепо стремиться к совершенству». Кстати, в этом отличие человека от машины. В принципе, по мнению Бубендорфера, речь идет о постоянном движении вверх, не о мгновении счастья на вершине как цели. «Путь этот долог, и чем умнее я его преодолеваю, тем дольше я в состоянии делать это хорошо». Износостойкость и постоянство качества — в этом созвучие, если проводить параллель с автомобилем.

Работоспособность и эффективность — вот что ценит Томас Бубендорфер в Porsche. И не только сидя за рулем Macan

Он хочет быть проводником, и не только на тропе Ницше. Протянутая открытая рука гораздо свойственнее ему, чем поднятый вверх указательный палец. Томас по натуре человек веселый, но сразу становится серьезным, говория о томм, что внимание числа людей следует настойчиво обращать на важность регенерации организма. Это существенная составляющая его теории Peak Performer. Многих эта тема действительно тяготит, они не находят решения, так как жизнь требует от них всё большей отдачи. Человек находится в вечной гонке, 24 часа в сутки.

В повседневной жизни бывают не только победы. «У разумной эффективности совсем иное начало и индикаторы. Конечно, количественные показатели важны, будь то спорт или экономика», говорит он. «Но речь уже идет о большем, нежели древний олимпийский девиз «Быстрее, выше, сильнее». Речь о достижениях устойчивых, щадящих человека и природу и, таким образом, сохраняющих значимость не только сегодня, но и в будущем». По смыслу: спортивный автомобиль есть пример того, к чему стремится человек. Продолжая образное сравнение, мы теперь должны бы спуститься в гараж. Среди установок, которыми не устает поражать нас ориентированный на результат Бубендорфер, есть такая: «Предпосылкой достижения является покой. Никуда не годится, если подверженный стрессу, невысыпающийся человек вздумает часами гонять на мотоцикле или бегать по лесу». Говоря о важности быть отдохнувшим, он особенно подчеркивает, что глубокий сон должен предшествовать движению: «Понизьте число оборотов, и получите требуемый максимум, когда будет нужно».

Бóльшая работоспособность означает для инструктора полное включение всего потенциала, что для его клиентов дает прежде всего повышение эффективности и креативности. Звучит понятно, даже как-то слишком просто. Томасу Бубендорферу, который в 21 год уже прочел свою первую лекцию менеджерам, подобные сомнения знакомы. У него на семинарах поэтому мало красивых слов, зато много непреложных фактов. Проводимый в спорте высоких достижений лактатный тест обязателен для установления идеальной интенсивности сердцебиения при высоких нагрузках. Кроме того, есть метод измерения вариабельности сердечного ритма как своего рода предупреждения «перегорания на работе». Это нормально, когда «мотор» человека в промежутке между пульсовыми ударами ведет себя, по возможности, неспокойно. Что лишь на первый взгляд кажется парадоксальным. Так создаются спортивно-медицинские таблицы, в которых содержатся результаты, результаты собственной жизни.

«Всё сделать правильно, можно лишь обладая правильными знаниями», уверен Томас Бубендорфер. Искусный перформанс — своего рода инструкция для организма. Но лежит она не в отделении для перчаток. Ее можно открыть только в самом себе.

Крутая карьера

Горы с детства притягивали к себе Томаса Бубендорфера.

Ему было всего 16, когда Томас Бубендорфер уже вошел в историю альпинизма, как самый юный скалолаз, в одиночку покорявший сложнейшие скалы. Потом было более 100 соло- восхождений в австрийских Альпах. В 18 лет он прошел по одному из труднейших маршрутов в Альпах, взобравшись по 900-метровой Северо-Западной стене Чиветты в Доломитах и став вторым в одиночных восхождениях. Он одолел путь за четыре часа. Первым был Райнхольд Месснер, которому на это понадобилось семь часов.

В 21 год Томас Бубендорфер совершал в своем соло-стиле и без страховки восхождения на самые высокие, сложные и опасные скалы Альп — северные стены Маттерхорна, Эйгера и Гран Жораса (регион Монблан). Частично он взбирался на вершины вдвое быстрее предшественников, пользовавшихся страховкой. Потом было еще много невероятных маршрутов в одиночку — Южная стена Аконкагуа (3 000 м) в Андах, которую Бубендорфер первым покорил за один день и без страховки. Он сорвался всего один раз, в 1988-м, на съемках рекламы. Падение с 20 метров в каменистое ущелье: девять сломанных позвонков и голеностопный сустав.

Получив 35-процентную инвалидность, Томас не отказался от трудных маршрутов. В последние двенадцать лет он специализировался в ледолазании по замерзшим водопадам, совершал первовосхождения в Гималаях, ходил экстремальные зимние маршруты. С 2000 года с различными напарниками ему удались более 30 чрезвычайно сложных первовосхождений в Альпах и Тибете. На скалах он проводит до 120 дней в году.

www.bubendorfer.com

Текст Элмар Брюммер
Фото Гюнтер Гёберль, Лоренцо Белфронд для GRIVEL, Штеффен Ян

Как измеряется крутящий момент Крутящий момент рассчитывается умножением силы F, прилагаемой к рычагу, на расстояние от точки вращения до точки приложения силы L (дл

Как измеряется крутящий момент Крутящий момент рассчитывается умножением силы F, прилагаемой к рычагу, на расстояние от точки вращения до точки приложения силы L (длина рычага). Математически это выражается следующим образом крутящий момент MA = Сила F x Рычаг L Принцип работы Сила F = 20 Н На схеме выше на 2 примерах показаны зависимости между силой F, рычагом L и крутящим моментом.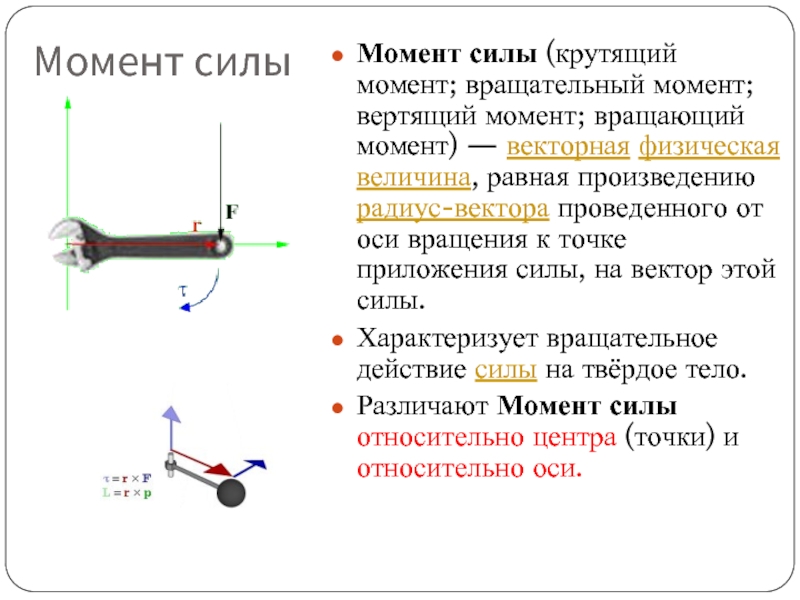 Для определения соответствующего крутящего момента мы используем формулу MA = F x L MA = F x L = 20 H x 1 = 20 Н-м (Ньютон на метр) MA = F x L = 20 H x 2 = 40 Н-м (Ньютон на метр) Это означает, что фактический крутящий момент, прилагаемый к винту, меняется при изменении положения руки на ключе. Применяется также для DREMASTER… Рукоятка, удобная для пользователя о Работа без ошибок DREMOMETER, тип MINI F В приборе DREMOMETER нам удалось обойти описанный выше физический принцип при помощи конструкционного приема. Независимо от того, в какой точке вы прилагаете силу, в середине рукоятки или в другой точке DREMOMETER, используете вы при этом обе руки или удлинитель установленный вами крутящий момент всегда достигается точно, без изменений значения Благодаря расположению на одной оси точки вращения и внешнего приводного квадрата, DREMOMETER это прибор, в работе которого не бывает неточностей. В отличие от обычных динамометрических ключей, единственный рычаг данного Дремометр с гайковертами прибора позволяет осуществлять затяжку без сдвигов в измеренном значении и без приложения усилий за пределами рукоятки, отрицательно влияющих на точность. Обратите внимание на то, что работать обычными динамометрическими ключами можно только прикладывая усилие в середине рукоятки, посколько в противном случае возможны значительные сдвиги значений. Вам нужна надежность Тогда выберите DREMOMETER. Установка крутящего момента (MxW) при использовании специальных насадок будет определяться следующей формулой MaxL к lw Установка крутящего момента = наш дремометр и SE работают по одному и тому же принципу. Позиция точки вращения смещается и вперед. Держать такие гаечные ключи следует за срединную часть рукояти. Однако, если вы пользуетесь концевыми штуцерами нашего гаечного ключа, настройку крутящего момента не придется заново рассчитывать по приведенной выше формуле. Просто держите в памяти глубинный калибр, приведенный в сертификате. Только в случае применения ваших собственных конструкций (т.е. изменив параметр L ) для настройки крутящего момента потребуется произвести новые расчеты. F = усилие MxW = установить крутящий момент, который должен быть настроен на шкале DREMOMETER MA = Крутящий момент затяжки винта или гайки lw = Расстояние от середины приводного квадрата DREMOMETER до середины рукоятки lx = Расстояние от середины приводного квадрата DREMOMETER до середины винта или гайки Когда дремометр используется в комплексе со специальным разводным ключом, длина упомянутого выше одинарного рычага не превышает длину корпуса. Наложенный ключ изменяет условия настолько, что точка вращения теперь находится за пределами операционных возможностей квадратного хвостовика и таким образом т.н. двойной рычаг оказывает свое воздействие на винтовое соединение. В результате величина нажима рукой F ассоциирована только со средней частью рукояти. Любая другая точка приложения усилия нажима неизбежно приведет к изменению этой величины. Зона подшипника рычага Ось вращения ось приложения усилия DREMOMETER, ТИП MINI F L L X w 259 смещенная точка вращения ДРЕМОМЕТР С ГАЙКОВЕРТАМИ Рычаг L = 1 Рычаг L = 2 м

Как определить крутящий момент электродвигателя

В данной статье осветим тему механических и электрических характеристик электродвигателей. На примере асинхронного двигателя рассмотрим такие параметры как мощность, работа, КПД, косинус фи, вращающий момент, угловая скорость, линейная скорость и частота. Все эти характеристики оказываются важными при проектировании оборудования, в котором электродвигатели служат в качестве приводных. Сегодня особенно широко распространены в промышленности именно асинхронные электродвигатели, поэтому на их характеристиках и остановимся. Для примера рассмотрим АИР80В2У3.

Номинальная механическая мощность асинхронного электродвигателя

На шильдике (на паспортной табличке) электродвигателя указывается всегда номинальная механическая мощность на валу данного двигателя. Это не та электрическая мощность, которую данный электродвигатель потребляет из сети.

Так, например, для двигателя АИР80В2У3, номинал в 2200 ватт соответствует именно механической мощности на валу. То есть в оптимальном рабочем режиме данный двигатель способен выполнять механическую работу 2200 джоулей каждую секунду. Обозначим эту мощность как P1 = 2200 Вт.

Номинальная активная электрическая мощность асинхронного электродвигателя

Чтобы определить номинальную активную электрическую мощность асинхронного электродвигателя, опираясь на данные с шильдика, необходимо принять в расчет КПД. Так, для данного электродвигателя КПД составляет 83%.

Что это значит? Это значит, что только часть активной мощности, подаваемой из сети на обмотки статора двигателя, и безвозвратно потребляемой двигателем, преобразуется в механическую мощность на валу. Активная мощность равна P = P1/КПД. Для нашего примера, по представленному шильдику видим, что P1 = 2200, КПД = 83%. Значит P = 2200/0,83 = 2650 Вт.

Номинальная полная электрическая мощность асинхронного электродвигателя

Полная электрическая мощность, подаваемая на статор электродвигателя от сети всегда больше механической мощности на валу и больше активной мощности, безвозвратно потребляемой электродвигателем.

Для нахождения полной мощности достаточно активную мощность разделить на косинус фи. Таким образом, полная мощность S = P/Cosφ. Для нашего примера P = 2650 Вт, Cosφ = 0,87. Следовательно полная мощность S = 2650/0,87 = 3046 ВА.

Номинальная реактивная электрическая мощность асинхронного электродвигателя

Часть полной мощности, подаваемой на обмотки статора асинхронного электродвигателя, возвращается в сеть. Это реактивная мощность Q.

Реактивная мощность связана с полной мощностью через sinφ, и связана с активной и с полной мощностью через квадратный корень. Для нашего примера:

Q = √( 3046 2 – 2650 2 ) = 1502 ВАР

Реактивная мощность Q измеряется в ВАР — в вольт-амперах реактивных.

Теперь давайте рассмотрим механические характеристики нашего асинхронного двигателя: номинальный рабочий момент на валу, угловую скорость, линейную скорость, частоту вращения ротора и ее связь с частотой питания электродвигателя.

Частота вращения ротора асинхронного электродвигателя

На шильдике мы видим, что при питании переменным током частотой в 50 Гц, ротор двигателя совершает при номинальной нагрузке 2870 оборотов в минуту, обозначим эту частоту как n1.

Что это значит? Поскольку магнитное поле в обмотках статора создается переменным током частотой 50 Гц, то для двигателя с одной парой полюсов (коим является АИР80В2У3) частота «вращения» магнитного поля, синхронная частота n, оказывается равной 3000 оборотов в минуту, что тождественно 50 оборотам в секунду. Но поскольку двигатель асинхронный, то ротор вращается с отставанием на величину скольжения s.

Значение s можно определить, разделив разность синхронной и асинхронной частот на синхронную частоту, и выразив это значение в процентах:

s = ( ( n – n1 )/ n) *100%

Для нашего примера s = ( (3000 – 2870)/3000 ) *100% = 4,3%.

Угловая скорость асинхронного двигателя

Угловая скорость ω выражается в радианах в секунду. Для определения угловой скорости достаточно частоту вращения ротора n1 перевести в обороты в секунду (f), и умножить на 2 Пи, поскольку один полный оборот составляет 2 Пи или 2*3,14159 радиан. Для двигателя АИР80В2У3 асинхронная частота n1 составляет 2870 оборотов в минуту, что соответствует 2870/60 = 47,833 оборотам в секунду.

Умножая на 2 Пи, имеем: 47,833*2*3,14159 = 300,543 рад/с. Можно перевести в градусы, для этого вместо 2 Пи подставить 360 градусов, тогда для нашего примера получится 360*47,833 = 17220 градусов в секунду. Однако подобные расчеты обычно ведут именно в радианах в секунду. Поэтому угловая скорость ω = 2*Пи*f, где f = n1/60.

Линейная скорость асинхронного электродвигателя

Линейная скорость v относится к оборудованию, на котором асинхронный двигатель установлен в качестве привода. Так, если на вал двигателя установлен шкив или, скажем, наждачный диск, известного радиуса R, то линейная скорость точки на краю шкива или диска может быть найдена по формуле:

Номинальный вращающий момент асинхронного двигателя

Каждый асинхронный электродвигатель характеризуется номинальным вращающим моментом Мн. Вращающий момент М связан с механической мощностью P1 через угловую скорость следующим образом:

Вращающий момент или момент силы, действующей на определенном расстоянии от центра вращения, для двигателя сохраняется, причем с ростом радиуса уменьшается сила, а чем радиус меньше, тем больше сила, поскольку:

Так, чем больше радиус шкива, тем меньшая сила действует на его краю, а наибольшая сила действует непосредственно на валу электродвигателя.

Для приведенного в качестве примера двигателя АИР80В2У3 мощность P1 равна 2200 Вт, а частота n1 равна 2870 оборотов в минуту или f = 47,833 оборота в секунду. Следовательно угловая скорость составляет 2*Пи*f, то есть 300,543 рад/с, и номинальный вращающий момент Мн равен P1/(2*Пи*f). Мн = 2200/(2*3,14159*47,833) = 7,32 Н*м.

Таким образом, исходя из данных, указанных на шильдике асинхронного электродвигателя, можно найти все основные электрические и механические его параметры.

Надеемся, что данная статья помогла вам разобраться в том, как связаны между собой угловая скорость, частота, вращающий момент, активная, полезная и полная мощность, а также КПД электродвигателя.

Этот калькулятор позволяет перевести мощность и момент силы и обратно для заданной угловой скорости

Ниже два калькулятора, которые переводят мощность в момент силы (или крутящий момент) и наоборот для заданной угловой скорости. Формулы под калькулятором.

Момент силы и мощность

Мощность и момент силы

Несколько формул/
Для мощности:

где P — мощность (Ватты или килоВатты), τ — крутящий момент (Ньютон-метр), ω — угловая скорость (радиан в секунду), а точка обозначает скалярное произведение.
Для момента силы:

Угловая скорость в калькуляторе задается в оборотах в минуту, приведение ее к радианам в секунду тривиально:

Одним из важных параметров электродвигателя, который так же важен при его выборе, является крутящий момент. Эта величина определяется произведением приложенной к плечу рычага силы и зависит исключительно от степени нагрузки. Если в двигателях внутреннего сгорания данную нагрузку задаётся коленчатым валом, то асинхронные электродвигатели получают величину крутящего момента от токов возбуждения. При этом величина этого момента будет зависеть от скорости вращающегося в магнитном поле статора устройства, называемого ротор. В зависимости от периода и способа определения, крутящий момент разделяют на:

• статический (пусковой) – минимальный момент холостого хода;
• промежуточный – развивает значение при работе двигателя от 0 величины оборотов до максимального значения в номинальной величине напряжения;
• максимальный – развивающийся при эксплуатации двигателя;
• номинальный – соответствует номинальным значениям мощности и оборотов.

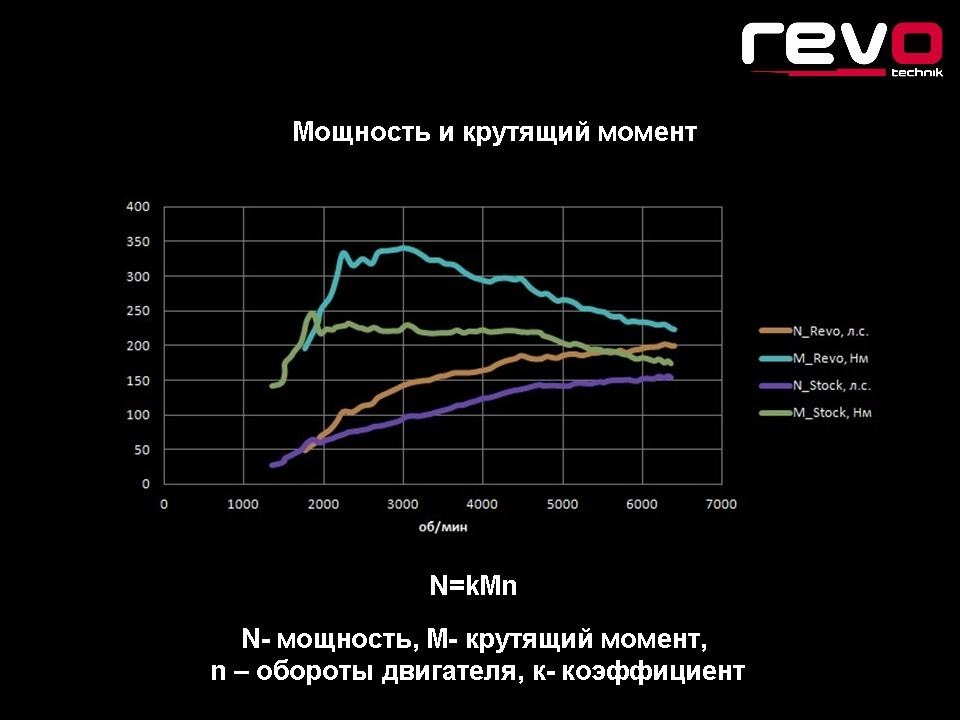
Для вычисления величины крутящего момента, определяющегося в «кгм» (килограмм на метр) или «Нм» (ньютон на метр), многие электротехнические пособия предлагают специальные формулы, учитывающие кроме основного действия вращающегося магнитного поля ряд всевозможных факторов, например:

• напряжения сети;
• величину индуктивного и активного сопротивления;
• зависимость от увеличения скольжения.

Но, рост скольжения не всегда приносит высокий момент. Зачастую, при достижении критических значений, наблюдается его резкое снижение. Такое явление обозначается как опрокидывающий момент. Одним из устройств, стабилизирующих скорость вращения ротора, а значит и величину момента кручения является частотный преобразователь, применение которого сейчас очень распространено во всех сферах, где от контроля работы двигателя зависит и успешность выполнения множественных производственных задач.

Выбираем электродвигатель по крутящему моменту

Для выбора, требуемого к выполнению тех или иных задач электродвигателя, берут в учёт практически все его характеристики, начиная от показателей мощности и заканчивая массогабаритными параметрами. Каждый из элементов по-своему важен в решении нюансов. Не меньшее значение припадает и на крутящий момент. Благодаря тому, что момент кручения напрямую связан с оборотами в соотношении: чем больше сами обороты, тем меньше будет момент, выбор электродвигателя будет исходить из следующих нюансов:

• из скоростных требований. В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях;
• по пусковым напряжениям. Здесь учитывается первичное усилие, например, для управления лифтом следует подбирать двигатели высокого пускового момента, способного поднимать большие грузы со старта. Хотя, многие статьи про электродвигатели рекомендуют так же применять устройства плавного пуска, умеющие обезопасить от нежелательных перегрузов.

Стоит помнить, что выбор осуществляется не по одному из показателей, даже при ориентировании относительно крутящего момента, ведь каждый из показателей ориентируется по рабочей предрасположенности электротехнического приводного устройства и его рабочих нагрузок в статистических и динамических эксплуатационных условиях, задаваемых самим предприятием.

Остались вопросы?
Специалисты ЭНЕРГОПУСК ответят на Ваши вопросы:
8-800-700-11-54 (8-18, Пн-Вт)

Альтернативный метод расчета крутящего момента и напряжения * — Физика тела: движение к метаболизму

Если вы не хотите думать о поиске плеч рычага, вместо этого вы можете рассчитать величину крутящего момента как величину силы, умноженную на полное расстояние до оси поворота, и на синус угла между силой и этим полным расстоянием. В форме уравнения это выглядит так:

(1)

Усиление деятельности

Крутящий момент, вызванный силой, зависит от угла между линией действия силы и линией, от которой сила прикладывается к точке поворота.Чтобы почувствовать этот эффект на себе, попробуйте это:

Поверните дверь, толкнув ее под углом 90 ° к двери прямо по внешнему краю.

Теперь приложите ту же силу к двери, все еще находясь на самом краю, но вместо того, чтобы толкать в направлении 90 ° к двери, толкайте ее вдоль двери прямо к петлям. Дверь распахивается, как раньше?

Во втором случае угол между направлением силы и расстоянием до оси был 0 ° (они были параллельны).Используйте предыдущее уравнение, чтобы показать, что крутящий момент должен быть равен нулю каждый раз, когда линия действия силы проходит прямо через точку вращения (шарнир).

Теперь мы знаем, что сила составляет 50 фунтов , расстояние от оси до груза составляет 13,0 на длины предплечья, а из диаграммы мы видим, что угол между весом мяча и расстоянием между предплечьями составляет 60 ° (то же, что угол бицепса и предплечья, потому что они являются альтернативными внутренними углами).Это легче увидеть, если мы нарисуем фигурную диаграмму:

Схема на палке согнутой руки, держащей мяч, показывающая напряжение и вес бицепса, а также углы между силами и предплечьем.

Теперь мы можем рассчитать крутящий момент от веса шара как:

Мы рассчитали крутящий момент на предплечье в зависимости от веса мяча. Возможно, вы привыкли слышать о крутящем моменте скорее в, но мы всегда можем преобразовать единицы позже, если захотим.А пока давайте продолжим работать над поиском мышечного напряжения.

Мы уже знаем, что крутящий момент из-за веса мяча равен, поэтому нам просто нужно убедиться, что напряжение в бицепсе достаточно велико, чтобы вызвать тот же крутящий момент, даже если он действует ближе к оси вращения. Крутящий момент мышцы двуглавой мышцы составляет:

Нам просто нужно сделать это равным крутящему моменту веса шара:

Затем делим обе стороны на и, чтобы изолировать напряжение бицепса:

Наконец, мы вводим наши значения для и.Наша исходная диаграмма дала нам расстояние от прикрепления бицепса к оси как 1,5 в , а из диаграммы с палкой мы видим, что угол между напряжением бицепса и расстоянием составляет 180 ° -60 ° = 120 °. Мы готовы найти величину напряжения бицепса.

Наш результат — 433 фунтов — кажется удивительно большим, но мы увидим, что силы даже большие, чем это, характерны для мышц, суставов и сухожилий тела.

Расчет крутящего момента как перекрестного произведения

Рассмотрим винт, показанный на схеме.Если силы применяются в разных местах, то как создаются эффекты вращения. Ось вращения проходит через центр винта и перпендикулярно плоскости схемы.
Сначала рассмотрите только силу F1 {F_1} F1, тогда будет ли она создавать какой-либо эффект вращения? Винт не будет вращаться, поэтому сила F1 {F_1} F1 не создаст крутящего момента.
Теперь, если приложить только силу F2 {F_2} F2, винт снова не будет вращаться.
Усилия F3 {F_3} F3 и F4 {F_4} F4 будут вращать винт, таким образом, они создадут некоторый крутящий момент или эффект поворота.Однако какой из них будет легко вращать винт? Сила F3 {F_3} F3 находится далеко от оси вращения и легко вращает винт по сравнению с F4 {F_4} F4.

F1 {F_1} F1 и F3 {F_3} F3 действуют в одной точке, но их угол разный. F1 {F_1} F1 и F3 {F_3} F3 имеют разные эффекты поворота. Итак, от каких факторов зависит эффект поворота?
Поскольку F3 {F_3} F3 и F4 {F_4} F4 создают крутящий момент, и они находятся на разных расстояниях от оси вращения, поэтому крутящий момент должен зависеть от расстояния силы от оси вращения.По этой причине ручки сделаны на концах дверей, так что расстояние силы увеличивается от оси вращения, и можно создать больший эффект поворота, применяя меньшее усилие.
Поскольку F1 {F_1} F1 и F3 {F_3} F3 находятся на одинаковом расстоянии от оси вращения, но под разными углами, крутящий момент зависит от ориентации силы.
Крутящий момент также зависит от величины силы. Чем больше сила, тем больше эффект поворота. Предположим, вы хотите открыть заклинивший винт, тогда вам нужно приложить большее усилие, чтобы получить больший крутящий момент.

Суммируя все вышеперечисленные факторы, можно сделать вывод, что относительно любой точки
τ⃗ = r⃗ × F⃗ \ vec \ tau = \ vec r \ times \ vec Fτ = r × F Здесь r⃗ \ vec rr — вектор положения точки приложения силы относительно точки, относительно которой должен быть вычислен крутящий момент,
F⃗ \ vec FF — приложенная сила,
τ⃗ \ vec \ tau τ — крутящий момент.
Направление крутящего момента можно рассчитать по правилам произведения.

Рассмотрим диаграмму выше, на которой угол между r⃗ \ vec rr и F⃗ \ vec FF равен θ \ thetaθ.В этом случае, если линия действия силы вытянута и на нее опущен перпендикуляр из точки расчета крутящего момента, то этот перпендикуляр называется плечом момента.
Плечо момента равно rsinθr sin \ thetarsinθ,
Величина крутящего момента относительно точки ‘O’ равна rFsinθr F sin \ theta rFsinθ,
Следовательно, крутящий момент также может быть записан как произведение силы и плеча момента.

ПРИМЕЧАНИЕ \ large \ color {# 3D99F6} {NOTE} ПРИМЕЧАНИЕ

Если крутящий момент должен быть рассчитан относительно точки на линии действия силы, то крутящий момент оказывается равным нулю.\ circ} 30∘ до гаечного ключа на расстоянии 8 см от гайки, он просто способен ослабить гайку. Какого усилия FFF будет достаточно для его ослабления, если оно действует перпендикулярно ключу на расстоянии 16 см от гайки?

Решение проблем с крутящим моментом

Решение проблемы чистого крутящего момента аналогично решению проблемы чистой силы, но с некоторыми отличиями. Для обоих типов проблем вам нужно найти сумму чего-либо: сил или моментов.Однако для проблем с чистой силой вы устанавливаете F net = ма , а для проблем с чистым крутящим моментом вы устанавливаете τ net = Iα . Вот еще несколько отличий: Для проблем с чистым крутящим моментом необходимо выбрать ось вращения, вокруг которой будут рассчитываться моменты плеч и крутящие моменты. Проблемы с чистой силой — это векторные проблемы. Вы решаете компоненты силы вдоль каждой оси. Для проблем с чистым крутящим моментом вы должны указать, как крутящий момент имеет тенденцию производить вращение по часовой стрелке или против часовой стрелки. Мы начнем с метода расчета чистого крутящего момента, а затем покажем, как найти угловое ускорение. Выберите ось вращения. Покажите на диаграмме выбранную ось. Нарисуйте силы, расширяющие с точки их применения. (Хотя это не было важно для Проблемы с чистой силой, это важно для проблем с крутящим моментом.) Нарисовать векторы положения от оси вращения до точек приложения каждого сил. Для каждой силы укажите угол, θ , от вектора положения до сила. Чтобы определить правильный угол, представьте, что r и F начинаются с одной и той же точки и согните пальцы вашей руки. правая рука от вектора положения к вектору силы.Угол между двумя векторами — это то, что вам нужно. Вектор может быть острый или тупой. Обязательно определите его правильно, потому что синус угла используется при вычислении плеча момента. Постройте плечо момента, каждой силы. Это может потребовать расширения линейки применения сила. Определите длину каждого момент руки используя. Запишите чистый крутящий момент уравнение,. Подставим величину каждый крутящий момент с использованием. Придайте каждому крутящему моменту правильный знак в соответствии с принятыми правилами имеют тенденцию производить против часовой стрелки +. Заменить заданные значения и Решите для чистого крутящего момента. Знак результата скажет вам является ли угловое ускорение из-за чистого крутящего момента по часовой стрелке или против часовой стрелки. Пример . Круглый диск вращается вокруг ось O через ее центр за счет приложения двух сил. Сила магнитудой 11 Н проявляется на расстоянии 0,34 м от оси и при угол 58 ° от радиальной линии, проходящей от оси через точку приложение Q силы.Вторая сила величиной 15 Н составляет воздействуют на расстоянии 0,26 м от оси и под углом 119 ° от радиальная линия, проходящая от оси через точку приложения P сила. Определите чистый крутящий момент на диске относительно его центра и каким образом чистый крутящий момент ускоряет диск. Дано : F 1 = 11 Н F 2 = 15 Н r 1 = 0. 34 м r 2 = 0,26 м θ 1 = 58 ° θ 2 = 119 ° Цель : Найдите τ net и направление угловое ускорение 1. Ось уже выбрана для нас в центре диска. 2. Силы исходят из точек P и Q. 3.Векторы положения взяты из точка O к точкам P и Q. 4. Угол, на который вектор положения превращается в силу вектор указан для каждой силы. См. Дополнительные диаграммы справа, чтобы узнать, как определяются углы. Теперь мы добавим несколько вспомогательных линий и углы на следующей диаграмме. (Две диаграммы обычно не необходимо, но мы предоставляем второй для ясности.) Расчетный момент рычага 5. Линия приложения F 1 была расширена, чтобы можно было нарисовать плечо силы. перпендикулярно линии нанесения. Плечо момента F 2 также нарисовано. 6. Плечо момента F 1 составляет против угла α, который равен θ 1 .Плечо момента F 2 противоположно углу β, который равен дополнительно к θ 2 . 7. Уравнение чистого крутящего момента: написано. Крутящий момент из-за F 1 (F 2 ) составляет отрицательный (положительный), потому что он имеет тенденцию производить по часовой стрелке (против часовой стрелки) вращение. Обратите внимание, что символы τ 1 и τ 2 представляют собой величины крутящих моментов.Знаки добавлены явно. Полученные выше выражения для плеча момента: заменены. 8. Значения указаны заменяется, и значение чистого крутящего момента определяется для. В результат положительный, что указывает на то, что угловое ускорение против часовой стрелки. Обратите внимание, что хотя единицы измерения — Нм, мы не называем их джоули. Джоуль используется для обозначения единицы работы или энергии. Крутящий момент — это не энергия. Когда известен чистый крутящий момент, вычисляют угловое ускорение, используя α = τ net / I , где I — момент инерции вращающегося твердого тела. Мы предлагаем следующее полное, примерное решение. Это ситуация, когда тонкий стержень с одинаковой плотностью шарнирно прикреплен к столу уровня одним концом. См. Рисунок 1 ниже. Масса стержня M , длина L .Теперь рассмотрим рисунок 2. Выбираем шарнир в точке А в качестве оси вращения. Обратите внимание, что нам не нужно выбирать физическую ось вращения в качестве точки для расчета крутящего момента. Однако в данной ситуации это удобно. Это потому, что шарнир воздействует на стержень, как для поддержки, так и для предотвращения горизонтального скольжения. Поскольку эти силы действуют через ось вращения, они имеют нулевые рычаги момента и, следовательно, создают нулевой момент. Таким образом, единственная сила, создающая крутящий момент, — это вес стержня Mg .Мы считаем эту силу действующей вертикально от центра масс. Плечо этой силы — это перпендикулярное расстояние AB от шарнира до линии действия силы. Это расстояние составляет AB = r cos θ , где r — расстояние от шарнира до центра масс. Вы можете задаться вопросом, почему мы используем здесь функцию косинуса, а не функцию синуса. Причина связана с тем, как определяется угол θ . При угле, показанном на диаграмме, перпендикулярное расстояние от оси вращения до линии приложения силы представляет собой сторону прямоугольного треугольника, смежную с θ .Таким образом, мы используем косинус. Теперь мы можем написать выражение для крутящего момента, создаваемого весом стержня. Поскольку стержень имеет однородную плотность, можно сказать, что центр масс находится в геометрическом центре стержня, таким образом, r = L /2 и AB = ( L / 2) cos θ . Таким образом, крутящий момент, создаваемый весом стержня, составляет τ Mg = — M g ( L / 2) cos θ . Знак минус означает, что крутящий момент производит вращение по часовой стрелке. Рисунок 1 Рисунок 2 Поскольку вес является единственной силой, создающей крутящий момент на стержне, тогда τ net = τ Mg = -Mg ( L / 2) cos θ . Теперь мы можем найти угловое ускорение. α = τ нетто / I = — M г ( L / 2) cos θ / I = — M г ( L / 2) cos θ / ( ML 2 /3) = — (3/2) (г / L ) cos θ Мы подставили выражение из Таблицы 10-1 текста для момента инерции тонкого стержня с осью на одном конце.Теперь сделаем несколько проверок. Мы уже обратились к вывеске. Единицы измерения справа (м / с 2 ) / м = 1 / с 2 , которые представляют собой единицы углового ускорения. Рассмотрим далее специальные значения угла. Когда θ = 90 o , α = 0. Это имеет смысл, потому что стержень будет вертикальным и находится в равновесии. (Обратите внимание, что равновесие неустойчиво, потому что даже небольшое движение позволило бы ему начать вращаться.) Когда θ = 0 o , α = — (3/2) (g / L ). Угловое ускорение достигает максимума непосредственно перед ударом стержня о стол. Это имеет смысл, потому что моментное плечо веса наибольшее в этой точке. Но имеет ли смысл величина (3/2) (г / л)? Рассмотрим тангенциальное ускорение в этой точке. Это вертикально вниз и определяется по величине как | a t | = L | α | = (3/2) г. Это говорит о том, что ускорение конца платы на 50% больше, чем g . Есть ли смысл в том, что ускорение падающего объекта может быть больше g ? Ответ — да, если предположить, что объект является частью вращающегося жесткого объекта, как в этой ситуации.Есть и другие точки объекта с касательными ускорениями менее g . Например, центр масс имеет | a CM | = ( L / 2) | α | = (3/4) г или 75% от г . Это говорит о том, что на стержне есть точка, имеющая тангенциальное ускорение g. Мы оставляем вам это упражнение, чтобы определить, где находится эта точка.

Основы определения размеров двигателя Часть 1: Момент нагрузки

Для правильного выбора двигателя необходимо выполнение трех критериев: крутящий момент, инерция нагрузки и скорость.В первой части этой серии статей по выбору двигателя я объясню, что такое крутящий момент нагрузки, как его рассчитать для конкретных примеров применения и как он соответствует требованиям к крутящему моменту для данного приложения.

Крутящий момент определяется как сила вращения на расстоянии от оси вращения. Он измеряется в таких единицах, как фунт-дюйм (фунт-дюйм) в британской системе мер или Нм (ньютон-метр) в метрической системе. Крутящий момент не менее важен, если не более важен, чем мощность двигателя. Лошадиная сила — это скорость, с которой работа может быть выполнена, и рассчитывается как крутящий момент, умноженный на скорость.Другими словами, крутящий момент — это способность выполнять работу, а мощность — это скорость, с которой работа может быть выполнена.

Крутящий момент состоит из двух основных компонентов: момента нагрузки и момента ускорения. Момент нагрузки — это величина крутящего момента, постоянно требуемая для приложения, включающая в себя фрикционную и гравитационную нагрузку. Момент ускорения — это крутящий момент, необходимый только для максимального ускорения и замедления нагрузки. Чем быстрее груз должен разогнаться, тем выше момент ускорения.Иногда момент нагрузки выше; иногда момент ускорения мог быть выше. Важно рассчитать и то, и другое; особенно для профилей быстрого движения.

На изображении выше мы показываем несколько стрелок, которые показывают направление сил, взаимодействующих в этом приложении. Как вы думаете, что такое момент нагрузки? Ответ — оба.

Момент нагрузки — это сумма нагрузок трения и гравитации. Сила тяжести определяется весом или массой x ускорением свободного падения ( г ).Сила трения, действующая в направлении, противоположном направлению движения конвейера, рассчитывается путем умножения массы груза на коэффициент трения двух поверхностей: м x µ .

Расчет момента нагрузки различается для разных приложений. Давайте рассмотрим несколько распространенных примеров, чтобы увидеть, как рассчитывается момент нагрузки.

Для шкивного привода расчет момента нагрузки довольно прост.Нам нужно создать силу на некотором расстоянии от вала двигателя (определение крутящего момента). Это можно рассчитать, умножив силу ( F ) на радиус вращения ( r ). Чтобы переместить нагрузку (синий прямоугольник), двигатель должен генерировать больший крутящий момент, чем это значение.

Для расчета крутящего момента нагрузки умножьте силу ( F ) на расстояние от оси вращения, которое является радиусом шкива ( r ) . Если масса груза (синяя рамка) составляет 20 Ньютонов, а радиус шкива составляет 5 см, то требуемый крутящий момент для приложения составляет 20 Н x 0.05 м = 1 Нм. Обычно используется коэффициент безопасности, чтобы двигатель генерировал больший крутящий момент, чем требуется, чтобы учесть любые неточности в переменных, используемых для расчета.

Вот формула для расчета момента нагрузки для шкивного привода со всеми переменными:

Приведенная выше формула работает для приложений с нагрузкой трения или без нее. Если вы удалите трение из системы (коэффициент трения скользящей поверхности µ = 0; внешняя сила FA = 0; передаточное число i = 1), вы, по сути, получите ту же основную формулу силы ( F ) x радиус ( r ).

Теперь давайте попробуем применить эту концепцию в другом приложении, которое имеет дело с трением.

В конвейере, где груз поддерживается поверхностью, трение постоянно и пропорционально массе груза. Степень скольжения на контактной поверхности или коэффициент трения ( µ) , необходима для определения силы трения ( F ).

Следующая формула используется для расчета момента нагрузки для ременных приводов (конвейеров), а также реечных и шестеренчатых передач.

Для этого типа применения нам нужно сначала рассчитать силу ( F ), прежде чем мы сможем рассчитать момент нагрузки ( TL ). Это требует от нас определения переменных внешней силы ( FA ), массы ( м, ) и угла наклона ( Θ ). Как только у нас будет значение F , мы можем подставить его в формулу момента нагрузки ( TL ).

Пример: поворотный индексный стол

При расчете крутящего момента

для поворотных столов используются те же формулы, что и для ременной передачи, но для определения необходимых переменных требуется несколько иной мыслительный процесс.В этом случае трение возникает в точках контакта шариковых роликов (опорных подшипников) и стола, поэтому радиус ( r ) будет расстоянием от центра вала двигателя до точки контакта между столом и его опорой. подшипники. Масса (м) будет массой стола плюс груз (ы). Коэффициент трения ( µ) обычно указывается в технических характеристиках подшипников.

СОВЕТ: Советы по выбору двигателя

1.Будьте осторожны, не смешивайте и не сопоставляйте британские и метрические единицы в одной формуле. 2. Если вам нужно преобразовать единицы, убедитесь, что они преобразованы правильно; особенно десятичная точка. 3. Используйте соответствующий коэффициент (-и) безопасности. Вы бы предпочли увеличить размер двигателя, чем уменьшить его. 4. Полезно иметь еще один свежий взгляд, чтобы дважды проверить свои расчеты. Сделайте жизнь проще. Используйте или.

Однако момент нагрузки — это лишь одна из двух составляющих полного крутящего момента, необходимого для данного приложения.Для правильного выбора двигателя нам по-прежнему необходимо рассчитать ускоряющий момент, инерцию нагрузки и скорость.

Следите за новостями, чтобы увидеть больше статей об основах определения размеров двигателя, когда я буду повторять каждый расчет.

Далее:

Рычаги и момент

Рычаги и момент

Рычаги и момент

Цели Рычаги исследования Рассчитать крутящий момент Рассчитать механическое преимущество

Настройка Метр Пружинная шкала Строка Масса.

Теория

Рычаги используют крутящий момент, чтобы помочь нам поднимать или перемещать объекты. Крутящий момент крест произведение между силой и расстоянием от нее до точки опоры (центральной точки о котором крутится система). Перекрестное произведение берет только компонент сила, действующая перпендикулярно расстоянию. С помощью тригонометрии определяется крутящий момент. как:

Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)

Помните, что работа также была силой, умноженной на расстояние, но это была точка произведение и использовал косинус угла между силой и расстоянием: сила × расстояние × cos (θ).

В этой лаборатории сила будет перпендикулярна (90 °) расстоянию. В синус 90 ° равен единице, поэтому крутящий момент будет:

Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)
Крутящий момент = Сила × Расстояние до точки опоры × sin (90 °)
Крутящий момент = Сила × Расстояние до точки опоры × 1
Крутящий момент = Сила × Расстояние до точки опоры

Процедура, сбор данных и расчеты

Пробный рычаг I класса: d

_e = d _r

В рычаге класса 1 точка опоры находится между силой сопротивления (F _r ) и сила усилия (F _e ). В классе один рычаг сила усилие (F _e ), умноженное на расстояние усилия от точки опоры (d _e ) равна силе сопротивления (F _r ), умноженной на расстояние сопротивление от точки опоры (d _r ). Усилие и сопротивление продолжаются противоположные стороны точки опоры. Плоскогубцы являются примером рычага первого класса.

На диаграмме масса обеспечивает сопротивление, пружинная шкала измеряет наши усилия. Пружинная шкала откалибрована в граммах.Граммы — это не единица измерения силы как таковой, но в этой лаборатории мы будем использовать термин «грамм-сила» как сила, действующая на один грамм у поверхности Земли за счет ускорения свободного падения. Один «грамм-сила» будет эквивалентна 980 см / сек ² (дин).

Для диаграммы: F _e × d _e = F _r × d _r
Механическое преимущество = F _r / F _e

1. Повесьте гирю 200 граммов на 10 см, подвесьте пружинную шкалу на 90 см, подвесьте измеритель на отметке 50 см.
2. Найдите F _e , d _e , F _r , d _r в граммах силы. Чтобы Определите грамм-силу массы (F _r ) с помощью весов балансира. d _e и d _r должен быть 40 см при правильной настройке. F _e можно прочитать по Весенняя граммовая шкала напрямую.
3. Вычислить F _e × d _e и F _r × d _r .
4. Укажите, является ли F _e × d _e = F _r × d _r .
5. Рассчитайте механическое преимущество F _r / F _e .

Ф. e	d e	F e × d e	F r	d r	F r × d r	F e d e = F r d r ?	M. A.
________	________	________	________	________	________	Да | Нет	________

Класс I Испытание рычагов два: d

_e > d _r

Для диаграммы: F _e × d _e = F _r × d _r
Механическое преимущество = F _r / F _e

1. Переключите массы на массу 500 грамм или две 200-граммовые гири все вместе.
2. Поместите груз массой 500 грамм на отметку 10 см и шкалу пружины на отметку 90 см, подвесьте метр от отметки 30 см.
3. Найдите F _e , d _e , F _r , d _r в граммах силы.
4. Вычислить F _e × d _e и F _r × d _r .
5. Укажите, является ли F _e × d _e = F _r × d _r .
6. Рассчитайте механическое преимущество F _r / F _e .

Ф. e	d e	F e × d e	F r	d r	F r × d r	F e d e = F r d r ?	M.A.
________	________	________	________	________	________	Да | Нет	________

Рычаги класса II

В рычаге второго класса сопротивление находится между силой усилия и силой точка опоры.В рычаге класса два сила усилия, умноженная на расстояние усилие от точки опоры противоположно и равно силе сопротивления умноженное на расстояние сопротивления от точки опоры. Усилия и Сопротивления находятся с одной стороны от точки опоры, но направлены в противоположные стороны.

Расстояние усилия (также иногда называемое «плечо усилия») на больше чем расстояние сопротивления.

Тачки и гигантские столбы для раскопок таро (когда мы отжимаемся на шесте) являются примерами рычаги второго класса.

Обратите внимание, что наш выбор пуха как положительного в первой части лабораторной работы означает, что up теперь отрицательный в этом разделе. Итак, F _e — отрицательная сила. Запишите F _e как отрицательное в таблице, а затем -F _e × d _e будет быть положительным.

Для диаграммы: -F _e × d _e = F _r × d _r
Механическое преимущество = | F _r / F _e | где | означает «абсолютный значение. «Механическое преимущество всегда положительно.

1. Переместите гирю 500 грамм (или две гири по 200 грамм) примерно на 30 см. Отметьте метку и пружинную шкалу на отметке 90 см, подвесьте измерительную штангу на отметке 10 см. Возможно, вам придется отрегулировать положение вашей массы в соответствии с возможностями вашего пружинная шкала для обеспечения точных показаний. Вы хотите избежать чтения очень маленькие граммовые силы или граммовые силы слишком большие для вашей пружинной шкалы. Если вы отрегулируете положения, не забудьте измерить фактические d _e и d _r , которые вы используете!
2. Найдите F _e , d _e , F _r , d _r в граммах силы.
3. Вычислить F _e × d _e и F _r × d _r .
4. Укажите, является ли -F _e × d _e = F _r × d _r .
5. Рассчитайте механическое преимущество F _r / F _e .

Ф. e	d e	-F e × d e	F r	d r	F r × d r	-F e d e = F r d r ?	М. А.
________	________	________	________	________	________	Да | Нет	________

Рычаги класса III

В рычаге третьего класса сопротивление находится между силой усилия и точка опоры. В рычаге третьего класса сила усилия, умноженная на расстояние усилия от точки опоры противоположны и равны силе сопротивления умноженное на расстояние сопротивления от точки опоры.Усилия и Сопротивления находятся с одной стороны от точки опоры, но направлены в противоположные стороны.

Расстояние усилия (также иногда называемое «рычагом усилия») на короче чем расстояние сопротивления.

Для диаграммы: -F _e × d _e = F _r × d _r
Механическое преимущество = | F _r / F _e | где | означает «абсолютный значение. «Механическое преимущество всегда положительно.

1. Перейти на массу 100 грамм.
2. Переместите гирю 100 грамм на отметку 90 см, а шкалу пружины примерно на отметку 65 см. см до отметки 70 см, удерживая измерительную линейку подвешенной на отметке 10 см. Еще раз при необходимости отрегулируйте шкалу пружины и положение масс, чтобы получить точные показания Весенняя шкала.
3. Найдите F _e , d _e , F _r , d _r в граммах силы.
4. Вычислить F _e × d _e и F _r × d _r .
5. Укажите, является ли -F _e × d _e = F _r × d _r .
6. Рассчитайте механическое преимущество F _r / F _e .

Ф. e	d e	-F e × d e	F r	d r	F r × d r	-F e d e = F r d r ?	М. А.
________	________	________	________	________	________	Да | Нет	________

В рычаге класса III механическое преимущество можно назвать механическим недостаток. Почему? (Предложение: примите во внимание силу усилия, меньше силы сопротивления или больше силы сопротивления?)

Обратите внимание, что нижняя часть руки человека является рычагом третьего класса: бицепс, прикрепленный чуть ниже локоть, можно использовать для поднятия груза, удерживаемого в руке в конце нижнего рука.

Рычаги прямого действия: Отвертки

Отвертка на самом деле представляет собой форму рычага, в которой ручка с большим радиусом обеспечивает механическое преимущество при повороте лезвия с меньшим радиусом. Всевозможные циркулярные устройства используют эту форму механического преимущества. Круглые ручки водяного клапана, шина утюги, торцевые ключи, гаечные ключи и многие другие предметы используют это время круговой рычаг.

Измерьте радиус ручки отвертки, а затем измерьте радиус лезвие.Рассчитайте механическое преимущество: d _e / d _r .

Обратите внимание, что механическое преимущество круглого устройства снижается, в то время как мех. нареч. для рычага было Fr / Fe. Обратите внимание, что кажущийся «триггер» дроби не ошибка.

Считаем, что F _e × d _e = F _r × d _r . Пересекать деление на F _e и d _r дает:

 d  e  = F  r 
- - = механическое преимущество
d  r  F  e  

SC 130 Домашняя страница
Домашняя страница курсов Ли Линга
На домашнюю страницу COM-FSM

Использование уравнений крутящего момента — AP Physics B

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Выполните следующие действия, чтобы отправить уведомление:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

21A: Векторы — Перекрестное произведение и крутящий момент

Не используйте левую руку при применении правила правой руки для векторного произведения двух векторов (обсуждаемого в этой главе) или правила правой руки для «чего-то фигурного, чего-то прямого», обсуждаемого в предыдущей главе.

Существует оператор отношения для векторов, который позволяет нам обойти вычисление плеча момента. Оператор отношения называется перекрестным произведением. Он представлен символом «×», читаемым «крестиком». Крутящий момент \ (\ vec {\ tau} \) можно выразить как перекрестное произведение вектора положения \ (\ vec {r} \) для точки приложения силы и вектора силы \ (\ vec { F} \):

\ [\ vec {\ tau} = \ vec {r} \ times \ vec {F} \ label {21-1} \]

Прежде чем мы начнем математическое обсуждение того, что мы подразумеваем под перекрестным произведением, уместно сказать несколько слов о векторе \ (\ vec {r} \).Для вас важно уметь различать вектор положения \ (\ vec {r} \) для силы и плечо момента, поэтому мы представим их ниже на одной и той же диаграмме. Мы используем тот же пример, который использовали ранее:

, в котором мы смотрим прямо вдоль оси вращения (чтобы она выглядела как точка), а сила лежит в плоскости, перпендикулярной этой оси вращения. Мы используем схематическое соглашение, согласно которому точка, в которой сила применяется к твердому телу, — это точка, в которой один конец стрелки на диаграмме касается твердого тела.Теперь добавим на диаграмму линию действия силы и плечо момента \ (r _ {\ bot} \), а также вектор положения \ (\ vec {r} \) точки приложения силы .

Плечо момента фактически может быть определено в терминах вектора положения для точки приложения силы. Рассмотрим наклонную систему координат \ (x \) — \ (y \), имеющую начало на оси вращения, с одной осью, параллельной линии действия силы, и одной осью, перпендикулярной линии действия силы .Мы помечаем ось \ (x \) \ (\ bot \) как «перпендикуляр», а ось \ (y \) \ (\ | \) как «параллель».

Теперь мы разбиваем вектор положения \ (\ vec {r} \) на составляющие его векторы вдоль осей \ (\ bot \) и \ (\ | \).

Из диаграммы видно, что плечо момента \ (r _ {\ bot} \) — это просто величина вектора составляющей в направлении, перпендикулярном силе, вектора положения точки приложения сила.

Теперь давайте обсудим кросс-продукт в общих чертах.Рассмотрим два вектора \ (\ vec {A} \) и (\ vec {B} \), которые не параллельны ни , ни антипараллельно друг другу. Два таких вектора определяют плоскость. Пусть эта плоскость будет плоскостью страницы и определим \ (\ theta \) как меньший из двух углов между двумя векторами, когда векторы нарисованы хвостом к хвосту.

Величина вектора векторного произведения \ (\ vec {A} \ times \ vec {B} \) определяется выражением

\ [| \ vec {A} \ times \ vec {B} | = AB sin \ theta \ label {21-2} \]

Удерживая пальцы на одной линии с предплечьем, укажите пальцами в направлении первого вектора (того, который стоит перед «\ (\ times \)» в математическом выражении для перекрестного произведения; e.г. \ (\ vec {A} \) в \ (vec {A} \ times \ vec {B} \)).

Теперь поверните руку по мере необходимости вокруг воображаемой оси, проходящей вдоль предплечья и среднего пальца, пока ваша рука не будет ориентирована так, что, если бы вы сомкнули пальцы, они указывали бы в направлении второго вектора.

Ваш большой палец теперь указывает в направлении вектора векторного произведения. \ (\ vec {C} = \ vec {A} \ times \ vec {B} \). Вектор перекрестного произведения \ (\ vec {C} \) всегда перпендикулярен обоим векторам, которые находятся в перекрестном произведении (\ (\ vec {A} \) и \ (\ vec {B} \) в случай под рукой).Следовательно, если вы нарисуете их так, чтобы оба вектора, которые находятся в перекрестном произведении, находились в плоскости страницы, вектор перекрестного произведения всегда будет перпендикулярен странице, либо прямо на страницу, либо прямо из страницы. . В данном случае это прямо со страницы.

Когда мы используем перекрестное произведение для вычисления крутящего момента от силы \ (\ vec {F} \), точка приложения которой имеет вектор положения \ (\ vec {r} \) относительно точки, вокруг которой мы находимся вычисляя крутящий момент, получаем вектор осевого крутящего момента \ (\ vec {\ tau} \).Чтобы определить направление вращения, которому будет соответствовать такой вектор крутящего момента, вокруг оси, определяемой самим вектором крутящего момента, мы используем Правило правой руки для чего-то Curly Something Straight. Обратите внимание, что мы вычисляем крутящий момент относительно точки, а не оси — ось, вокруг которой действует крутящий момент, выходит в ответ.

Вычисление перекрестного произведения векторов, заданных в \ (\ hat {i} \), \ (\ hat {j} \), \ (\ hat {k} \) Обозначение

Единичные векторы позволяют напрямую вычислить перекрестное произведение двух векторов даже в самых общих обстоятельствах, например.г. обстоятельства, при которых каждый из векторов указывает в произвольном направлении в трехмерном пространстве. Чтобы воспользоваться преимуществом этого метода, нам нужно знать векторное произведение единичных векторов декартовых координатных осей \ (\ hat {i} \), \ (\ hat {j} \) и \ (\ hat {k} \) друг с другом.

Прежде всего, отметим, что любой вектор, пересекающийся сам с собой, дает ноль. Это видно из уравнения \ (\ ref {21-2} \):

\ [| \ vec {A} \ times \ vec {B} | = AB sin \ theta \]

, потому что если A и B находятся в одном направлении, то \ (\ theta = 0 ^ {\ circ} \), а поскольку \ (sin0 ^ {\ circ} = 0 \), мы имеем \ (| \ vec { A} \ times \ vec {B} | = 0 \). {\ circ} = 1 \ ) так

\ [| \ vec {A} \ times \ vec {B} | = AB \]

Теперь, если \ (\ vec {A} \) и \ (\ vec {B} \) — единичные векторы, то их величины равны 1, так что произведение их величин также равно 1.Более того, единичные векторы \ (\ hat {i} \), \ (\ hat {j} \) и \ (\ hat {k} \) все перпендикулярны друг другу, поэтому величина перекрестного произведения любого из них из них с любым другим из них является произведением двух величин, то есть 1.

А как насчет направления? Давайте воспользуемся правилом правой руки, чтобы получить направление \ (\ hat {i} \ times \ hat {j} \):

С пальцами правой руки, указывающими прямо от правого локтя и в том же направлении, что и \ (hat {i} \), (первый вектор в ‘\ (\ hat {i} \ times \ hat {j } \) ‘), чтобы сделать так, чтобы если бы кто-то сомкнул пальцы, они указывали бы в том же направлении, что и \ (\ hat {j} \), ладонь должна быть обращена в направлении + y.В этом случае вытянутый большой палец должен указывать в направлении + z. Объединяя информацию о величине (величина каждого единичного вектора равна 1) и направлении (+ z), мы видим, что \ (\ hat {i} \ times \ hat {j} = \ hat {k} \). Аналогично: \ (\ hat {j} \ times \ hat {k} = \ hat {i} \), \ (\ hat {k} \ times \ hat {i} = \ hat {j} \), \ ( \ hat {j} \ times \ hat {i} = — \ hat {k} \), \ (\ hat {k} \ times \ hat {j} = — \ hat {i} \) и \ (\ шляпа {i} \ times \ hat {k} = — \ hat {j} \). Один из способов запомнить это — написать \ (\ hat {i} \), \ (\ hat {j} \), \ (\ hat {k} \) дважды подряд:

\ [\ hat {i}, \ hat {j}, \ hat {k}, \ hat {i}, \ hat {j}, \ hat {k} \]

Затем пересечение любого из первых трех векторов в векторе, расположенном непосредственно справа от него, дает следующий вектор справа.Но пересечение любого из последних трех векторов в вектор, находящийся непосредственно слева от него, дает отрицательное значение для следующего вектора слева (слева направо «+», но справа налево «-»).

Теперь мы готовы рассмотреть общий случай. Любой вектор \ (\ vec {A} \) можно выразить через единичные векторы:

\ [\ vec {A} = A_x \ hat {i} + A_y \ hat {j} + A_z \ hat {k} \]

Проделав то же самое для вектора \ (\ vec {B} \), мы можем записать кросс-произведение как:

\ [\ vec {A} \ times \ vec {B} = (A_x \ hat {i} + A_y \ hat {j} + A_z \ hat {k}) \ times (B_x \ hat {i} + B_y \ шляпа {j} + B_z \ hat {k}) \]

Используя правило распределения для умножения, мы можем записать это как:

\ [\ vec {A} \ times \ vec {B} = A_x \ hat {i} \ times (B_x \ hat {i} + B_y \ hat {j} + B_z \ hat {k}) + A_y \ hat {j} \ times (B_x \ hat {i} + B_y \ hat {j} + B_z \ hat {k}) + A_z \ hat {k} \ times (B_x \ hat {i} + B_y \ hat {j} + B_z \ hat {k}) \]

\ [\ vec {A} \ times \ vec {B} = A_x \ hat {i} \ times B_x \ hat {i} + A_x \ hat {i} \ times B_y \ hat {j} + A_x \ hat { i} \ times B_z \ hat {k} + A_y \ hat {j} \ times B_x \ hat {i} + A_y \ hat {j} \ times B_y \ hat {j} + A_y \ hat {j} \ times B_z \ hat {k} + A_z \ hat {k} \ times B_x \ hat {i} + A_z \ hat {k} \ times B_y \ hat {j} + A_z \ hat {k} \ times B_z \ hat {k} \]

Используя в каждом члене правило коммутативности и ассоциативное правило умножения, мы можем записать это как:

\ [\ vec {A} \ times \ vec {B} = A_x B_x (\ hat {i} \ times \ hat {i}) + A_x B_y (\ hat {i} \ times \ hat {j}) + A_x B_z (\ hat {i} \ times \ hat {k}) + A_y B_x (\ hat {j} \ times \ hat {i}) + A_y B_y (\ hat {j} \ times \ hat {j}) + A_y B_z (\ hat {j} \ times \ hat {k}) + A_z B_x (\ hat {k} \ times \ hat {i}) + A_z B_y (\ hat {k} \ times \ hat {j} ) + A_z B_z (\ hat {k} \ times \ hat {k}) \]

Теперь оценим перекрестное произведение, которое встречается в каждом термине:

\ [\ vec {A} \ times \ vec {B} = A_x B_x (0) + A_x B_y (\ hat {k}) + A_x B_z (- \ hat {j}) + A_y B_x (- \ hat { k}) + A_y B_y (0) + A_y B_z (\ hat {i}) + A_z B_x (\ hat {j}) + A_z B_y (- \ hat {i}) + A_z B_z (0) \]

Исключение нулевых членов и группирование членов с \ (\ hat {i} \) вместе, членов с \ (\ hat {j} \) вместе и членов с \ (\ hat {k} \) вместе дает :

\ [\ vec {A} \ times \ vec {B} = A_y B_z (\ hat {i}) + A_z B_y (- \ hat {i}) + A_z B_x (\ hat {j}) + A_x B_z ( — \ hat {j}) + A_x B_y (\ hat {k}) + A_y B_x (- \ hat {k}) \]

Выделение единичных векторов дает:

\ [\ vec {A} \ times \ vec {B} = (A_y B_z- A_z B_y) \ hat {i} + (A_z B_x — A_x B_z) \ hat {j} + (A_x B_y- A_y B_x) \ шляпа {k} \]

, которое можно записать в одной строке как:

\ [\ vec {A} \ times \ vec {B} = (A_y B_z- A_z B_y) \ hat {i} + (A_z B_x — A_x B_z) \ hat {j} + (A_x B_y- A_y B_x) \ шляпа {k} \ label {21-3} \]

Это наш конечный результат. Мы сможем прийти к этому результату гораздо быстрее, если позаимствуем инструмент из этой области математики, известной как линейная алгебра (математика матриц).

Формируем матрицу \ (3 \ times 3 \)

\ [\ begin {bmatrix} \ hat {i} & \ hat {j} & \ hat {k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \ end {bmatrix} \]

, записав \ hat {i}, \ hat {j}, \ hat {k} в качестве первой строки, затем компоненты первого вектора, который появляется в перекрестном произведении в качестве второй строки, и, наконец, компоненты второй вектор, который отображается в перекрестном произведении в последней строке.Оказывается, перекрестное произведение равно определителю этой матрицы. Мы используем знаки абсолютного значения на всей матрице, чтобы обозначить «определитель матрицы». Итак, имеем:

\ [\ vec {A} \ times \ vec {B} = \ begin {vmatrix} \ hat {i} & \ hat {j} & \ hat {k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \ end {vmatrix} \ label {21-4} \]

Чтобы взять определитель матрицы \ (3 \ умножить на 3 \), вы проделываете свой путь через верхнюю строку. Для каждого элемента в этой строке вы берете произведение элементов по диагонали, идущей вниз и вправо, за вычетом произведения элементов вниз и влево; и вы складываете три результата (по одному результату для каждого элемента в верхней строке) вместе.Если вниз и на соответствующую сторону нет элементов, вы переходите на другую сторону матрицы (см. Ниже), чтобы завершить диагональ.

Для первого элемента первой строки, \ (\ hat {i} \), переместите произведение вниз и вправо,

(это дает \ (\ hat {i} A_yB_z \))

минус произведение вниз и влево

(произведение слева и снизу: \ (\ hat {i} A_zB_y \))

Для первого элемента в первой строке мы, таким образом, имеем: \ (\ hat {i} A_yB_z- \ hat {i} A_zB_y \), который можно записать как: \ ((A_yB_z-A_zB_y) \ hat {i} \ ).Повторяя процесс для второго и третьего элементов в первой строке (\ (\ hat {j} \) и \ (\ hat {k} \)), мы получаем \ ((A_zB_x — A_xB_z) \ hat {j} \) и \ ((A_xB_y — A_yB_x) \ hat {k} \) соответственно.