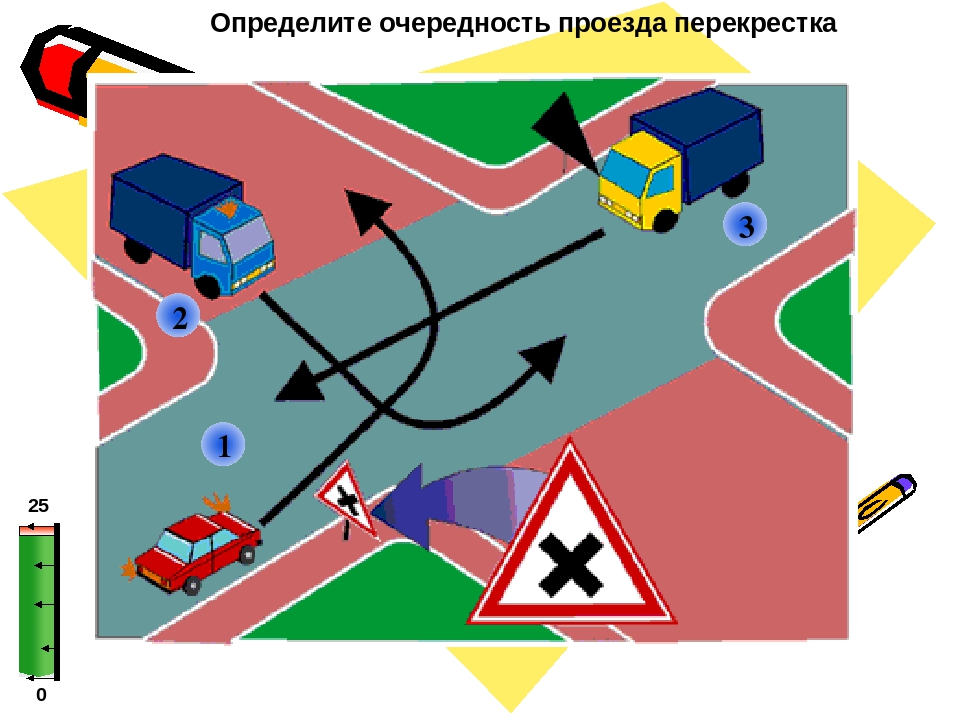
Как определить тип перекрестка?
Добрый день, уважаемый читатель.
В предшествующей статье серии «Правила проезда перекрестков» речь шла о выборе правильной полосы движения перед перекрестком.
Вторая задача, которую необходимо решить до въезда на перекресток, — это правильно определить разновидность перекрестка, т.к. именно от этого зависят правила проезда.
Для разных видов перекрестков применяются разные пункты правил дорожного движения.
Виды перекрестков
Регулируемые перекрестки
Первым делом на любом перекрестке нужно проверить, является он регулируемым или нет. Поэтому при подъезде к перекрестку нужно попытаться найти взглядом регулировщика. Встретить регулировщика на перекрестке можно не очень часто, однако именно он является самым приоритетным признаком регулируемого перекрестка.
Регулировщик делает регулируемым абсолютно любой перекресток, даже любое пересечение полевых или лесных дорог.
Только в том случае, если Вам не удалось найти регулировщика, следует обратить внимание на светофоры. С их поиском проблем обычно не возникает, т.к. светофор можно заметить издалека.
С их поиском проблем обычно не возникает, т.к. светофор можно заметить издалека.
Если на перекрестке есть светофор, то это еще не означает, что перекресток является регулируемым. Для начала нужно разобраться с режимом работы светофора. Если светофор работает в нормальном режиме (красный-желтый-зеленый), то перекресток регулируемый и можно вздохнуть спокойно.
Если же светофор работает в мигающем желтом режиме или выключен, то перекресток является нерегулируемым и придется приложить еще немного усилий, чтобы разобраться с его типом.
Нерегулируемые перекрестки
На нерегулируемом перекрестке водитель должен определить, является ли пересечение равнозначным или нет. А в случае неравнозначного перекрестка нужно дополнительно понять, на главной или второстепенной дороге Вы находитесь.
1. Главная дорога
Если перед перекресток установлен один из перечисленных выше знаков (2.1, 2.3.1-2.3.7, 5.1), то можно утверждать что Ваш автомобиль въезжает по главной дороге.
2. Второстепенная дорога
Дорожные знаки 2.4 и 2.5 подсказывают водителю, что он въезжает на перекресток по второстепенной дороге.
3. Равнозначный перекресток
Знак 1.6 перед перекрестком означает, что Вы въезжаете на перекресток равнозначных дорог.
Отдельного внимания заслуживает дорожный знак 2.2 «Конец главной дороги»:
Внимание! Многие водители допускают распространенную ошибку и считают, что знак 2.2 говорит о том, что автомобиль находится на второстепенной дороге. Это не так.
Если перед перекрестком не оказалось представленных выше знаков, определяющих приоритет проезда, либо оказался только знак 2.2, то придется приложить еще немного усилий, чтобы разобраться с типом перекрестка.
Перекрестки без знаков
Перекрестки без знаков встречаются на дорогах не очень часто. Тем не менее водитель должен уметь ориентироваться и на них.
Обратимся к пункту 1.2 правил дорожного движения:
«Главная дорога» – дорога, обозначенная знаками 2.
1, 2.3.1 – 2.3.7 или 5.1, по отношению к пересекаемой (примыкающей), или дорога с твердым покрытием (асфальто- и цементобетон, каменные материалы и тому подобное) по отношению к грунтовой, либо любая дорога по отношению к выездам с прилегающих территорий. Наличие на второстепенной дороге непосредственно перед перекрестком участка с покрытием не делает ее равной по значению с пересекаемой.
Чтобы определить вид перекрестка без знаков, следует разобраться с тем, какой тип покрытия имеет каждая из дорог.
1. Если покрытие одинаковое, то перекресток равнозначный.
2. Если Вы отчетливо видите, что на одной из дорог покрытие грунтовое (земля, песок, глина и т.п.), а на другой дороге — твердое (асфальт, цементобетон, щебень и т.п.), то перекресток неравнозначный. В этом случае главной дорогой является та, которая имеет твердое покрытие.
Отдельного внимания заслуживает ситуация, когда водитель не может определить тип покрытия. Например, на улице темно, идет дождь или на дорогах лежит снег. В этом случае нужно руководствоваться пунктом 13.13 правил дорожного движения:
В этом случае нужно руководствоваться пунктом 13.13 правил дорожного движения:
13.13. Если водитель не может определить наличие покрытия на дороге (темное время суток, грязь, снег и тому подобное), а знаков приоритета нет, он должен считать, что находится на второстепенной дороге.
В этой статье рассмотрены правила, связанные с определением типа перекрестка. Ну а в следующей речь пойдет о правилах на перекрестке с регулировщиком.
Удачи на дорогах!
Как определить тип перекрестка?
Добрый день, уважаемый читатель.
В предшествующей статье серии «Правила проезда перекрестков» речь шла о выборе правильной полосы движения перед перекрестком.
Вторая задача, которую необходимо решить до въезда на перекресток, — это правильно определить разновидность перекрестка, т.к. именно от этого зависят правила проезда.
Для разных видов перекрестков применяются разные пункты правил дорожного движения.
Виды перекрестков
Регулируемые перекрестки
Первым делом на любом перекрестке нужно проверить, является он регулируемым или нет. Поэтому при подъезде к перекрестку нужно попытаться найти взглядом регулировщика. Встретить регулировщика на перекрестке можно не очень часто, однако именно он является самым приоритетным признаком регулируемого перекрестка.
Поэтому при подъезде к перекрестку нужно попытаться найти взглядом регулировщика. Встретить регулировщика на перекрестке можно не очень часто, однако именно он является самым приоритетным признаком регулируемого перекрестка.
Регулировщик делает регулируемым абсолютно любой перекресток, даже любое пересечение полевых или лесных дорог.
Только в том случае, если Вам не удалось найти регулировщика, следует обратить внимание на светофоры. С их поиском проблем обычно не возникает, т.к. светофор можно заметить издалека.
Если на перекрестке есть светофор, то это еще не означает, что перекресток является регулируемым. Для начала нужно разобраться с режимом работы светофора. Если светофор работает в нормальном режиме (красный-желтый-зеленый), то перекресток регулируемый и можно вздохнуть спокойно.
Если же светофор работает в мигающем желтом режиме или выключен, то перекресток является нерегулируемым и придется приложить еще немного усилий, чтобы разобраться с его типом.
Нерегулируемые перекрестки
На нерегулируемом перекрестке водитель должен определить, является ли пересечение равнозначным или нет. А в случае неравнозначного перекрестка нужно дополнительно понять, на главной или второстепенной дороге Вы находитесь.
1. Главная дорога
Если перед перекресток установлен один из перечисленных выше знаков (2.1, 2.3.1-2.3.7, 5.1), то можно утверждать что Ваш автомобиль въезжает по главной дороге.
2. Второстепенная дорога
Дорожные знаки 2.4 и 2.5 подсказывают водителю, что он въезжает на перекресток по второстепенной дороге.
3. Равнозначный перекресток
Знак 1.6 перед перекрестком означает, что Вы въезжаете на перекресток равнозначных дорог.
Отдельного внимания заслуживает дорожный знак 2.2 «Конец главной дороги»:
Внимание! Многие водители допускают распространенную ошибку и считают, что знак 2.2 говорит о том, что автомобиль находится на второстепенной дороге.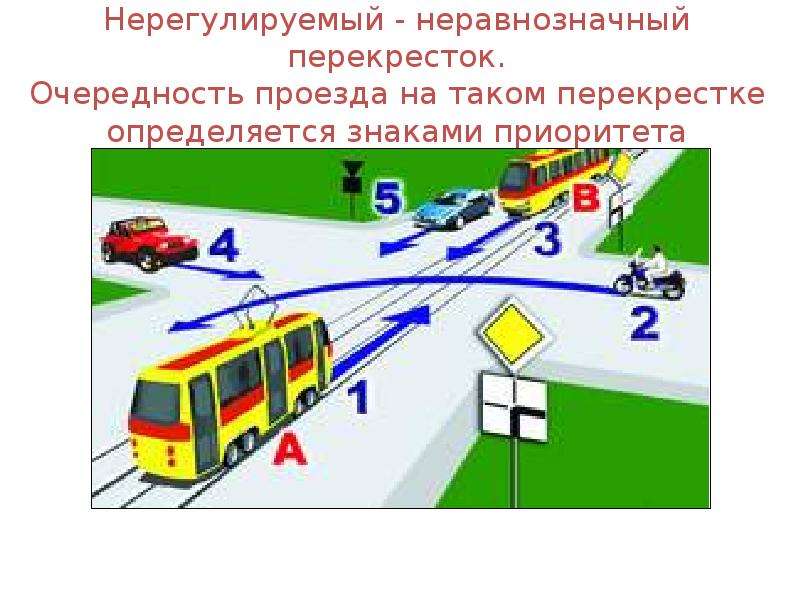 Это не так.
Это не так.
Если перед перекрестком не оказалось представленных выше знаков, определяющих приоритет проезда, либо оказался только знак 2.2, то придется приложить еще немного усилий, чтобы разобраться с типом перекрестка.
Перекрестки без знаков
Перекрестки без знаков встречаются на дорогах не очень часто. Тем не менее водитель должен уметь ориентироваться и на них.
Обратимся к пункту 1.2 правил дорожного движения:
«Главная дорога» – дорога, обозначенная знаками 2.1, 2.3.1 – 2.3.7 или 5.1, по отношению к пересекаемой (примыкающей), или дорога с твердым покрытием (асфальто- и цементобетон, каменные материалы и тому подобное) по отношению к грунтовой, либо любая дорога по отношению к выездам с прилегающих территорий. Наличие на второстепенной дороге непосредственно перед перекрестком участка с покрытием не делает ее равной по значению с пересекаемой.
Чтобы определить вид перекрестка без знаков, следует разобраться с тем, какой тип покрытия имеет каждая из дорог.
1. Если покрытие одинаковое, то перекресток равнозначный.
2. Если Вы отчетливо видите, что на одной из дорог покрытие грунтовое (земля, песок, глина и т.п.), а на другой дороге — твердое (асфальт, цементобетон, щебень и т.п.), то перекресток неравнозначный. В этом случае главной дорогой является та, которая имеет твердое покрытие.
Отдельного внимания заслуживает ситуация, когда водитель не может определить тип покрытия. Например, на улице темно, идет дождь или на дорогах лежит снег. В этом случае нужно руководствоваться пунктом 13.13 правил дорожного движения:
13.13. Если водитель не может определить наличие покрытия на дороге (темное время суток, грязь, снег и тому подобное), а знаков приоритета нет, он должен считать, что находится на второстепенной дороге.
В этой статье рассмотрены правила, связанные с определением типа перекрестка. Ну а в следующей речь пойдет о правилах на перекрестке с регулировщиком.
Удачи на дорогах!
Как определить тип перекрестка?
Добрый день, уважаемый читатель.
В предшествующей статье серии «Правила проезда перекрестков» речь шла о выборе правильной полосы движения перед перекрестком.
Вторая задача, которую необходимо решить до въезда на перекресток, — это правильно определить разновидность перекрестка, т.к. именно от этого зависят правила проезда.
Для разных видов перекрестков применяются разные пункты правил дорожного движения.
Виды перекрестков
Регулируемые перекрестки
Первым делом на любом перекрестке нужно проверить, является он регулируемым или нет. Поэтому при подъезде к перекрестку нужно попытаться найти взглядом регулировщика. Встретить регулировщика на перекрестке можно не очень часто, однако именно он является самым приоритетным признаком регулируемого перекрестка.
Регулировщик делает регулируемым абсолютно любой перекресток, даже любое пересечение полевых или лесных дорог.
Только в том случае, если Вам не удалось найти регулировщика, следует обратить внимание на светофоры. С их поиском проблем обычно не возникает, т.к. светофор можно заметить издалека.
Если на перекрестке есть светофор, то это еще не означает, что перекресток является регулируемым. Для начала нужно разобраться с режимом работы светофора. Если светофор работает в нормальном режиме (красный-желтый-зеленый), то перекресток регулируемый и можно вздохнуть спокойно.
Если же светофор работает в мигающем желтом режиме или выключен, то перекресток является нерегулируемым и придется приложить еще немного усилий, чтобы разобраться с его типом.
Нерегулируемые перекрестки
На нерегулируемом перекрестке водитель должен определить, является ли пересечение равнозначным или нет. А в случае неравнозначного перекрестка нужно дополнительно понять, на главной или второстепенной дороге Вы находитесь.
1. Главная дорога
Если перед перекресток установлен один из перечисленных выше знаков (2. 1, 2.3.1-2.3.7, 5.1), то можно утверждать что Ваш автомобиль въезжает по главной дороге.
1, 2.3.1-2.3.7, 5.1), то можно утверждать что Ваш автомобиль въезжает по главной дороге.
2. Второстепенная дорога
Дорожные знаки 2.4 и 2.5 подсказывают водителю, что он въезжает на перекресток по второстепенной дороге.
3. Равнозначный перекресток
Знак 1.6 перед перекрестком означает, что Вы въезжаете на перекресток равнозначных дорог.
Отдельного внимания заслуживает дорожный знак 2.2 «Конец главной дороги»:
Внимание! Многие водители допускают распространенную ошибку и считают, что знак 2.2 говорит о том, что автомобиль находится на второстепенной дороге. Это не так.
Если перед перекрестком не оказалось представленных выше знаков, определяющих приоритет проезда, либо оказался только знак 2.2, то придется приложить еще немного усилий, чтобы разобраться с типом перекрестка.
Перекрестки без знаков
Перекрестки без знаков встречаются на дорогах не очень часто. Тем не менее водитель должен уметь ориентироваться и на них.
Тем не менее водитель должен уметь ориентироваться и на них.
Обратимся к пункту 1.2 правил дорожного движения:
«Главная дорога» – дорога, обозначенная знаками 2.1, 2.3.1 – 2.3.7 или 5.1, по отношению к пересекаемой (примыкающей), или дорога с твердым покрытием (асфальто- и цементобетон, каменные материалы и тому подобное) по отношению к грунтовой, либо любая дорога по отношению к выездам с прилегающих территорий. Наличие на второстепенной дороге непосредственно перед перекрестком участка с покрытием не делает ее равной по значению с пересекаемой.
Чтобы определить вид перекрестка без знаков, следует разобраться с тем, какой тип покрытия имеет каждая из дорог.
1. Если покрытие одинаковое, то перекресток равнозначный.
2. Если Вы отчетливо видите, что на одной из дорог покрытие грунтовое (земля, песок, глина и т.п.), а на другой дороге — твердое (асфальт, цементобетон, щебень и т.п.), то перекресток неравнозначный. В этом случае главной дорогой является та, которая имеет твердое покрытие.
Отдельного внимания заслуживает ситуация, когда водитель не может определить тип покрытия. Например, на улице темно, идет дождь или на дорогах лежит снег. В этом случае нужно руководствоваться пунктом 13.13 правил дорожного движения:
13.13. Если водитель не может определить наличие покрытия на дороге (темное время суток, грязь, снег и тому подобное), а знаков приоритета нет, он должен считать, что находится на второстепенной дороге.
В этой статье рассмотрены правила, связанные с определением типа перекрестка. Ну а в следующей речь пойдет о правилах на перекрестке с регулировщиком.
Удачи на дорогах!
В помощь начинающему водителю. Проезд нерегулируемых перекрестков
В помощь начинающему водителю. Проезд нерегулируемых перекрестков.
В предыдущих статьях мы разбирали движение через регулируемые (светофором или регулировщиком) перекрестки. В этой — опишем порядок движения через нерегулируемые перекрестки.
Для начала необходимо понять, что подъезжая к любому перекрестку, сперва необходимо определить его тип. Для этого смотрим, управляет ли порядком движения светофор или регулировщик, т.е. светофор работает в режиме «красный-желтый-зеленый» или порядком движения управляет регулировщик.
1. Если это так, то перекресток является регулируемым и на знаки приоритета водитель не обращает ни какого внимания. На регулируемых перекрестках нет дороги главной, нет – второстепенной.
2. Если светофор/регулировщик отсутствуют, или не занимаются регулированием дорожного движения – светофор работает в режиме желтого мигающего огня или выключен, сотрудник ДПС контролирует соблюдение водителями Правил Дорожного Движения, то такой перекресток будет НЕРЕГУЛИРУЕМЫМ. И первое на что водитель должен обращать внимание, что должен искать своими глазами – знаки приоритета.
2.1 Если знаки приоритета имеют место быть, то такой перекресток является НЕРАВНОЗНАЧНЫМ, или как его правильно называть НЕРЕГУЛИРУЕМЫЙ ПЕРЕКРЕСТОК НЕРАВНОЗНАЧНЫХ ДОРОГ. Неравнозначных дорого означает, что одна дорога является главной и приближающийся по не транспорт пользуется преимущественным правом на проезд перекрестка.
Неравнозначных дорого означает, что одна дорога является главной и приближающийся по не транспорт пользуется преимущественным правом на проезд перекрестка.
Если знаки приоритета отсутствуют, то водитель должен обратить внимание, на то какими дорогами организован перекресток. Если он образуется дорогой с твердым покрытием по отношению к грунтовой дороге, то это так же будет нерегулируемый перекресток неравнозначных дорог
. Дорога с твердым покрытием будет являться главной по отношению к грунтовой дороге.Тут необходимо уточнить тот факт, что любое твердое покрытие – класс твердого покрытия роли не играет. В тоже время дороги с разными твердыми покрытиями между собой равны. Например: дорога с асфальтом и гравийная дорога – образуют РАВНОЗНАЧНЫЙ ПЕРЕКРЕСТОК. Булыжная мостовая и грунтовая дорога – НЕРАВНОЗНАЧНЫЙ ПЕРЕКРЕСТОК.
2.2 Ну и как уже сказано если условия «разности» дорожного покрытия не выполняется – то это РАВНОЗНАЧНЫЙ ПЕРЕКРЕСТОК. Или как правильно назвать – НЕРЕГУЛИРУЕМЫЙ ПЕРЕКРЕСТОК РАВНОЗНАЧНЫХ ДОРОГ, т.е. приближающийся к такому перекрестку транспорт находится в равных дорожных условиях.
Или как правильно назвать – НЕРЕГУЛИРУЕМЫЙ ПЕРЕКРЕСТОК РАВНОЗНАЧНЫХ ДОРОГ, т.е. приближающийся к такому перекрестку транспорт находится в равных дорожных условиях.
Таким образом, если изобразить все вышеописанное графически, то получим следующее:
Из приведенной схемы следует, что существует всего три типа перекрестков которые могут встретиться на просторах нашей Родины:
1. Регулируемые
2. Нерегулируемые неравнозначных дорог
3. Нерегулируемые равнозначных дорог
Еще раз хотелось бы подчеркнуть, что форма перекрестка и место его расположения роли не играют. Для каждого типа существуют свои правила проезда.
В одной автошколе на экзамене группа более чем 30 человек экзамен по вождению в городе не сдала, только потому, что «инспектор принимал экзамен не на том маршруте, по которому они с инструктором ездили». Ученик не знал, как проезжать конкретный перекресток, на котором проходил экзаменационный маршрут.
Еще раз – правила проезда всех форм перекрестков едины. Надо только определить его тип и двигаться исходя из этого.
Надо только определить его тип и двигаться исходя из этого.
Итак, в этой статье мы разберем движение через нерегулируемые перекрестки.
НЕРЕГУЛИРУЕМЫЕ ПЕРЕКРЕСТКИ РАВНОЗНАЧНЫХ ДОРОГ
Прежде чем начнем разбирать движение по таким перекресткам, необходимо понять — по каким признакам мы можем сделать вывод о том, что перекресток перед нами равнозначный. А именно:
1. Знак 1.6 (рис.1)
2. Равное дорожное покрытие и отсутствие знаков приоритета. Еще раз подчеркну – не одинаковое, а равное – либо твердое, либо грунтовое.
В той или иной степени правило проезда равнозначных перекрестков слышали многие. Правило которое звучит, как «Правило правой руки» — п.13.11 ПДД на перекрестке равнозначных дорог водитель безрельсового транспортного средства обязан уступить дорогу транспортным средствам приближающимся справа (рис.2)
Необходимо уточнить, что требование «уступить дорогу» будет возникать если траектории транспортных средств пересекаются или сливаются. Если пересечений или слияний нет, то требование не возникает (рис.3,4).
Если пересечений или слияний нет, то требование не возникает (рис.3,4).
Также необходимо прописать порядок движения трамваев. В случаях равного права на проезд трамвай пользуется преимуществом в движении в независимости от траектории его дальнейшего движения (рис.5).
Тут необходимо понять, что следует избегать так называемого движения «под прикрытием» трамвая. Казалось бы почему (авт.3 из рис.5) не поехать одновременно с трамваем, (авт.2 из рис.5) будет все равно трамвай пропускать. Делать этого не стоит.
Согласно требований Правил (авт.2) обязан выполнить требование «уступить дорогу» применительно к трамваю. Требование «уступить дорогу» в данной ситуации означает, что трамвай не должен изменять скорость или траекторию движения. Учитывая специфику движения трамвая – он едет по строго выделенной колее (рельсы), то даже выехав за границу пересечения проезжих частей (но не выезжая на трамвайные пути) (авт.2) дорогу трамваю уступит, а вот (авт.3) скорее всего, совершит с ним столкновение (рис.
Так же не лишним, считаю проговорить ситуацию, изображенную в одном из экзаменационных билетов. К четырехстороннему перекрестку приближается четыре транспортных средства и все хотят проехать прямо (рис.7).
Кому такой вопрос попадался сразу отвечают, что «правила такую ситуацию не оговаривают и водители разъезжаются по договоренности». Однако если спросить почему не оговаривают и что значит по договоренности? Ответ уже не находится.
По договоренности это как?
Все просто, кто-то кого-то должен пропустить. Один уезжает и конфликтной ситуации уже нет. Для этого мы можем махнуть рукой, мигнуть фарами или еще как-нибудь показать что мы пропускаем.
Почему Правила не регламентируют эту ситуацию?
Все очень просто. Вспомните много ли у нас регулируемых перекрестков скажем в дачных поселках? Их нет вообще! Происходит это потому, что там нет интенсивности в движении. Равнозначными оставляют те перекрестки, где указанная ситуация – подъехало четверо и всем необходимо прямо (стоит только одному повернуть направо и трудностей нет) – редкое явление.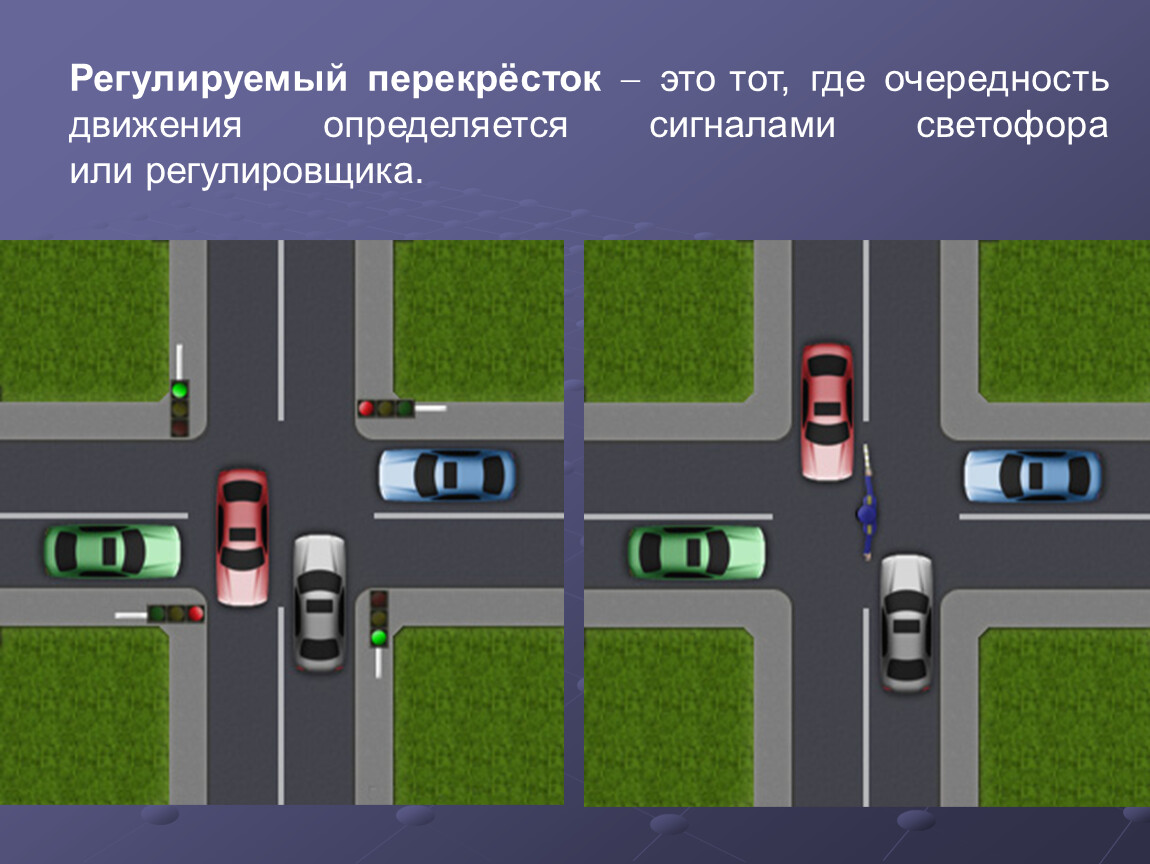
Таким образом, правила проезда нерегулируемых перекрестков равнозначных дорог можно сформировать в следующих тезисах:
1. Первыми проезжают перекресток трамваи. Если их несколько, а траектории движения пересекаются, то уступает дорогу тот, у кого имеется помеха справа.
2. Во вторую очередь такой перекресток проезжают безрельсовые транспортные средства между собой по помехам (рис.8)
3. Если приближается спецтранспорт с включенными синими проблесковыми маячками и специальным звуковым сигналом, то вне зависимости от траектории его движения он покидает перекресток в первую очередь.
4. Если безрельсовый транспорт совершает левый поворот – пропускает (уступает дорогу) встречным транспортным средствам двигающимся прямо или направо.
НЕРЕГУЛИРУЕМЫЕ ПЕРЕКРЕСТКИ НЕРАВНОЗНАЧНЫХ ДОРОГ
Начнем с признаков главной дороги:
1. Главной является дорога обозначенная знаками 2.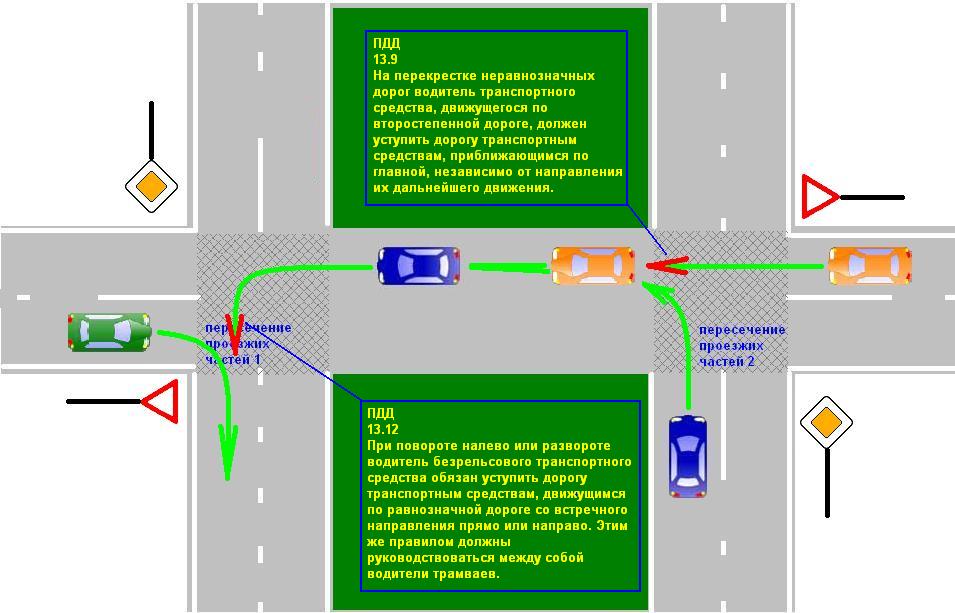 1, 2.3.1, 2.3.2, 2.3.3, 2.3.4, 2.3.5, 2.3.6, 2.3.7 а также 5.1 (рис.9), т.е. если водитель видит один из указанных знаков, значит он находится на главной дороге. При движении по второстепенной дороге этих знаков водитель не увидит.
1, 2.3.1, 2.3.2, 2.3.3, 2.3.4, 2.3.5, 2.3.6, 2.3.7 а также 5.1 (рис.9), т.е. если водитель видит один из указанных знаков, значит он находится на главной дороге. При движении по второстепенной дороге этих знаков водитель не увидит.
2. Дорога с твердым покрытием по отношению к грунтовой дороге.
3. Любая дорога по отношению к выезду с прилегающей территории.
Дополнительно хотелось бы акцентировать внимание на двух дорожных знаках 2.4, 2.5 (рис. 10).
Оба этих знака обязывают водителя УСТУПАТЬ (не создавать помех) дорогу.
Знак 2.5 помимо прочего обязывает ОБЯЗАТЕЛЬНО зафиксировать остановку. Устанавливают в тех местах где не зафиксировав остановку водитель не сможет принять однозначно верного решения о возможности проезда перекрестка. Какое-то решение принято будет, но оно не будет однозначно верным. Пример: перекресток пр-т. Невского – ул. Луначарского. Стоящие в плотную дома очень ограничивают видимость и не зафиксировав остановку водитель может попасть в ДТП.
Еще раз оговорюсь требование «УСТУПИ ДОРОГУ» не говорит, откуда и как приближается транспорт, находящийся на главной дороге. Водители, находящиеся на второстепенной дороге не должны вынуждать его изменять скорость или направление движения. При движении по главной дороге даже разрешен обгон – т.е. транспорт может ехать по встречной полосе.
Знак 2.4 – устанавливают в тех местах, где водитель еще только приближаясь к перекрестку уже может определить будет он создавать помехи или нет. Если своим движением не создается помех транспортным средствам, приближающимся по главной дороге – можно проследовать безостановочно.
Если главная дорога не меняет своего направления на перекрестке, то трудностей возникать не должно. Транспорт, приближающийся по главной дороге, пользуется преимущественным правом движения через перекресток. Транспорт, двигающийся по второстепенной дороге, обязан уступать дорогу. Трамваи, находящиеся в равных дорожных условиях с безрельсовыми транспортными средствами – проезжают в первую очередь. (рис.11)
(рис.11)
Трудности могут возникать в случаях, когда главная дорога меняет на перекрестке свое направление (рис.12)
Сложность проезда такого перекрестка заключается в том, что траектории движения транспортных средств, находящихся в равных дорожных условиях могут пересекаться (рис.13)
В таких ситуациях необходимо вспомнить уже известное нам правило «правой руки» — уступи тому кто приближается справа. Это относится ко всем водителям, приближающимся к такому перекрестку и находящимся в равных дорожных условиях.
Таким образом, получаем следующий порядок в движении:
1. Первыми покидают перекресток трамваи находящиеся на главной дороге.
2. Вторыми безрельсовые транспортные средства находящиеся на главной дороге, если их траектории пересекаются, то разъезжаются согласно правил проезда равнозначных перекрестков (уступи тому кто справа).
3. В третью очередь трамваи на второстепенной дороге
4. И последними покидают такой перекресток безрельсовые транспортные средства, находящиеся на второстепенной дороге – между собой по помехам. (рис.14)
(рис.14)
Отдельно хотелось бы напомнить водителям пункт 13.1 Правил: При поворотах направо-налево водитель ОБЯЗАН уступить дорогу пешеходам переходящим проезжую часть на которую он поворачивает. Зачастую водители высказывают мнение, что если пешеходный переход отсутствует, то дорогу уступать не надо. Это не верно. Согласно п.4.3 Правил продолжение линий тротуаров или обочин проходящих через перекресток служат для движения пешеходов (рис.15).
Соблюдая вышеприведенные рекомендации Вы, скорее всего, не станете виновником ДТП.
PS статья является личным мнением автора
Александр Медников
См. также: Лекция: Помощь начинающему водителю. Перекрёсток
Лекция: Помощь начинающему водителю. Светофоры с дополнительными секциями
Лекция: Ручное регулирование перекрёстка
Внимание, организационное собрание состоится 4 ноября в 19 часов
.Тема 13.3. Проезд перекрестков. Нерегулируемые перекрестки неравнозначных дорог — Учебник
Если движением на регулируемом перекрестке «заведуют» светофоры и регулировщики, то на нерегулируемом пересечении дорог водителям приходится самостоятельно решать, кто проедет первым. Не из головы, конечно. Ведь теме проезда перекрестков посвящена целая глава в ПДД.
Не из головы, конечно. Ведь теме проезда перекрестков посвящена целая глава в ПДД.
Чтобы перекресток считался неравнозначным, перед ним должны быть установлены знаки приоритета.
Если вы подъехали к нерегулируемому перекрестку неравнозначных дорог со стороны второстепенной дороги, уступите дорогу всем, кто въезжает на пересечение с главной, независимо от того, куда они потом повернут.
Итак, сначала разъезжаются водители главной дороги. Разъезжаются они с учетом правила «помеха справа», то есть если траектории движения машин, которые находятся на главной дороге, не пересекаются, то они едут одновременно. Если же их траектории пересекаются, уступает водитель, у которого есть помеха справа. Только после этого разъезжаются водители второстепенной дороги (также по принципу «помеха справа»).
Водители второстепенной дороги стоят и дисциплинированно ждут, пока не разъедутся водители главной дороги. Для «второстепенных» не важно, как это будет происходить. Будут ли «главные» продолжать движение по главной дороге или будут поворачивать на второстепенную – от этого их приоритет не заканчивается.
Положение рассматривается с момента старта на перекрестке. Если водитель перед въездом на пересечение находится на главной дороге, то его приоритет по отношению к водителям второстепенной дороги не прекращается, пока он не освободит перекресток.
А вот трамвай на нерегулируемом перекрестке неравнозначных дорог пропускать придется не всегда.
Рельсовое транспортное средство имеет приоритет только перед теми, кто въезжает с второстепенной или с равнозначной с трамваем дороги.
Если же трамвай находится на второстепенной дороге, он теряет свое преимущество по отношению к водителям главной дороги. Ведь трамвай имеет приоритет только при равных условиях.
Ведь трамвай имеет приоритет только при равных условиях.
Отдельно стоит упомянуть про перекрестки с круговым движением.
При въезде на такой перекресток принцип «помехи справа» не работает. И если нет никаких знаков приоритета, то круг по умолчанию – главная дорога. А значит, придется уступить тем, кто уже кружится.
Иногда главная дорога на перекрестке меняет свое направление.
Об этом может свидетельствовать знак «Направление главной дороги» (указан стрелкой на фото).
Порядок разъезда на перекрестке остается прежним.
Вначале разъезжаются водители главной дороги по принципу «помехи справа». Затем пересечение покидают водители второстепенной дороги. При разъезде они также должны руководствоваться «правилом правой руки». Аналогично разъезжаются между собой и водители трамваев. Но при равных условиях рельсовое транспортное средство автомобилисту придется пропустить.
Аналогично разъезжаются между собой и водители трамваев. Но при равных условиях рельсовое транспортное средство автомобилисту придется пропустить.
Чтобы понять, в какой последовательности транспортные средства должны проезжать нерегулируемый перекресток неравнозначных дорог, давайте решим несколько экзаменационных задач.
Кому Вы обязаны уступить дорогу при повороте налево?
1. Трамваям А и Б.
2. Трамваю А и легковому автомобилю.
3. Только трамваю А.
4. Никому.
Первый вопрос, который необходимо задать: кто находится на главной дороге? Именно эти водители обладают преимуществом при проезде.
В данном случае на главной дороге находимся мы, синий автомобиль и трамвай А. Вначале разъезжаются эти транспортные средства.
При равных условиях, трамвай А имеет преимущество по отношению к другим участникам дорожного движения, поэтому он проедет первым, а мы должны ему уступить.
Трамвай Б, который находится на второстепенной дороге, как помеха не рассматривается. А синий автомобиль по отношению к нам находится слева, значит ему мы не уступаем.
Верный ответ – 3.
Поскольку в решении задач участвует множество факторов, можно что-то упустить. Поэтому предлагаем вам действовать по определенному алгоритму при решении задач проезда неравнозначных перекрестков.
1. Кто на главной дороге?
2. Есть ли помеха справа?
3. Выводим ответ.
Потренируемся.
Кому Вы должны уступить дорогу при движении прямо?
1. Легковому автомобилю и мотоциклу.
2. Только легковому автомобилю.
3. Никому.
Работаем по схеме, приведенной выше.
1. Определяем, кто находится на главной дороге? Смотрим на знак «Направление главной дороги» . На главной дороге – мы и водитель легкового автомобиля. Поскольку грузовик и мотоцикл находятся на второстепенной дороге по отношению к нам, уступать мы им не обязаны.
Поскольку грузовик и мотоцикл находятся на второстепенной дороге по отношению к нам, уступать мы им не обязаны.
2. Следующий вопрос: есть ли у нас помеха справа? Водитель легковушки находится справа от нас, а значит он – «помеха справа».
3. Выводим ответ: уступаем только водителю легкового автомобиля. Правильный ответ – 2.
Задача решена. Мы ничего не упустили.
Разберем еще один пример.
При движении прямо Вы обязаны уступить дорогу:
1. Только легковому автомобилю.
2. Автобусу и легковому автомобилю.
3. Всем транспортным средствам.
1. Кто на главной дороге? Смотрим на знак «Направление главной дороги» . На главной дороге автобус и легковой автомобиль. Поскольку мы находимся на второстепенной дороге, а они – на главной, мы им уступаем. Обоим.
2. Есть ли помеха справа? Теперь смотрим, кто находится с нами на второстепенной дороге? Мотоцикл. Он по отношению к нам – слева. Поэтому мы ему не уступаем.
Он по отношению к нам – слева. Поэтому мы ему не уступаем.
3. Выводим ответ: уступаем только автобусу и легковому автомобилю. Правильный вариант – 2.
При решении задачи мы все учли.
Есть в экзаменационном тестировании серия задач, которые вызывают некоторые сложности у кандидатов в водители из-за своей неочевидности.
Например, вот эта:
Вы намерены повернуть направо. Можете ли Вы приступить к повороту?
1. Можете.
2. Можете, когда убедитесь, что при этом не будут созданы помехи грузовому автомобилю.
3. Не можете.
Водитель грузового автомобиля едет по другой полосе, мы с ним не пересекаемся. И хочется ответить, что можем. Но не все так просто.
Грузовик едет по главной дороге, и он может перестроиться на правую полосу прямо на перекрестке. В этот момент он не обязан учитывать водителя, который находится на второстепенной дороге. Если мы начнем движение, то в этом случае произойдет ДТП. Кто будет виноват? Исходя из требований знака «Уступите дорогу» – мы… Поэтому правильный ответ в данном случае будет – 2. Мы должны убедиться, что не создадим помех водителям главной дороги. Упор здесь делается на знак «Уступите дорогу» .
Если мы начнем движение, то в этом случае произойдет ДТП. Кто будет виноват? Исходя из требований знака «Уступите дорогу» – мы… Поэтому правильный ответ в данном случае будет – 2. Мы должны убедиться, что не создадим помех водителям главной дороги. Упор здесь делается на знак «Уступите дорогу» .
Аналогично нужно отвечать и на следующую задачу.
Можете ли Вы в данной ситуации приступить к повороту налево?
1. Можете.
2. Можете, только убедившись в том, что не создадите помех встречному автомобилю, выполняющему поворот налево.
3. Не можете.
Грузовик, который находится на главной дороге, тоже делает левый поворот. Если бы разъезд происходил на равнозначном перекрестке, то оба водителя разъехались бы одновременно, не пересекая центр перекрестка. Но перед нами стоит знак «Уступите дорогу» . Исходя из требований знака, мы должны убедиться, что не создадим помех грузовику.
Возможно, грузовик едет с прицепом. Поскольку при повороте прицеп смещается к центру радиуса поворота, водителям с прицепом рекомендуется делать радиус поворота больше. И, естественно, в этой ситуации наши траектории пересекутся. Произойдет ДТП. Кто будет виноват? Исходя из требований знака «Уступите дорогу» – мы. Так что верный ответ в этой и подобных задачах всегда – 2 (сначала надо убедиться, что мы не создаем помех).
Поскольку при повороте прицеп смещается к центру радиуса поворота, водителям с прицепом рекомендуется делать радиус поворота больше. И, естественно, в этой ситуации наши траектории пересекутся. Произойдет ДТП. Кто будет виноват? Исходя из требований знака «Уступите дорогу» – мы. Так что верный ответ в этой и подобных задачах всегда – 2 (сначала надо убедиться, что мы не создаем помех).
Ну и напоследок заметим то, что на дороге часто бывает недостаточная видимость.
Если вы не видите дальше собственного капота и не можете определить наличие покрытия на дороге (темное время суток, грязь, снег и т.п.), а знаков приоритета нет, то считайте, что вы находитесь на второстепенной дороге.
А значит уступайте дорогу другим транспортным средствам и будьте предельно осторожны.
Равнозначная дорога: что это?
Хотите пройти тест по материалам статьи после ее прочтения?
ДаНет
Территория нашей большой страны покрыта не только главными транспортными путями, но и маленькими дорогами. Они не оснащены светофорами или другими регулировщиками движения, а называются такие пути «равнозначные дороги». Могут образовывать собой перекрестки. Предупреждает об их наличии знак 1.6.Несмотря на отсутствие контроля, движение по распутьям осуществляется по определенным правилам.
Они не оснащены светофорами или другими регулировщиками движения, а называются такие пути «равнозначные дороги». Могут образовывать собой перекрестки. Предупреждает об их наличии знак 1.6.Несмотря на отсутствие контроля, движение по распутьям осуществляется по определенным правилам.
Что такое равнозначная дорога
Подобные транспортные пути, как правило, имеют асфальтовое покрытие не высокого качества. Возле них так же зачастую отсутствует любое регулирующие устройство: знак, светофор, лежачий полицейский. Похожие дороги находятся в сельской местности. Только там на смену асфальту приходит грунтовое покрытие. Возникает вопрос, как такие пути квалифицировать и проезжать?
Подобные дороги принято считать равными. Законодательство расшифровывает значение понятия по-своему. Согласно действующим ПДД, равнозначная (равная) дорога это:
- часть транспортного пути;
- отсутствие светофора, регулировщика;
- имеет асфальтовое или грунтовое покрытие;
- на ней отсутствует разрешительный знак.

Сами по себе такие пути для опытных водителей не несут сложностей, а вот новички ощущают себя не так уверенно, проезжая такие участки полотен. Особенно часто возникают сложности при движении через распутье равнозначных дорог, ведь другое транспортное средство может неожиданно возникнуть из-за поворота. Внимательность плюс четкое соблюдение правил помогают избежать конфликтных ситуаций.
Понятие перекрестка равнозначных дорог
Пересечение двух равных путей довольно частый феномен в городе или селе. Называется такое явление «перекресток равнозначных дорог». Для обозначения используют знак под номером 1.6. Он представляет собой треугольник с красной рамкой. Внутри изображено пересечение черных прямых линий.
Распутье за пределами больших населенных пунктов, как правило, указателями не оснащено.
Можно встретить два вида пересечения. Самый распространенный способ – это распутье, когда две дороги размещены перпендикулярно одна к другой.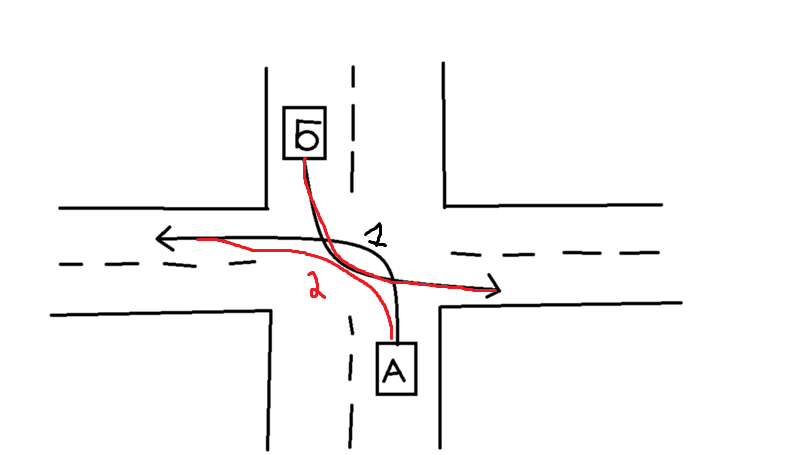 Встречается реже, но не менее важен Т-образный перекресток, когда сходятся вместе 3 дороги и движения прямо нет. Нормы проезда по обоим типам дорожных полотен одинаковы. Главное, соблюдать правило правой стороны. Его суть в следующем: куда бы водитель ни ехал, он должен пропустить транспортные средства, находящиеся справа от него, т. е. помеху справа.
Встречается реже, но не менее важен Т-образный перекресток, когда сходятся вместе 3 дороги и движения прямо нет. Нормы проезда по обоим типам дорожных полотен одинаковы. Главное, соблюдать правило правой стороны. Его суть в следующем: куда бы водитель ни ехал, он должен пропустить транспортные средства, находящиеся справа от него, т. е. помеху справа.
Правила проезда через перекрестки
Проезжая главную магистраль, человек за рулем чувствует себя увереннее, ведь по ПДД ему должны уступить место водители с прилегающих дорог. Сложнее автомобилистам на равнозначных транспортных путях — там все в одинаковых условиях. Разбираться, кто пропускает, а кто уступает, нужно моментально. Убережет от необдуманных действий снижение скорости. Перед перекрестком равнозначных дорог устанавливается знак 1.6, он и является главным сигналом к притормаживанию.
Автомобилист не может предугадать что его ждет за поворотом. Спасает в таких случаях быстрая оценка ситуации и три правила проезда подобных участков дорог. Основные принципы движения:
Основные принципы движения:
- Рельсовое транспортное средство проезжает в первую очередь. Это правило также касается рейсовых автобусов.
- Другие автомобили, находящиеся по правую сторону от водителя, имеют над ним преимущество. Их необходимо пропустить.
- В первую очередь уступают дорогу автомобилям, которые движутся по прямой линии. Затем транспортным средствам сворачивающим направо.
Основные действия водителя при повороте направо
Подобный маневр легко выполнимый. Главное, правильно оценить ситуацию на предмет наличия пешеходов или рельсовых транспортных средств. Далее совершить правый поворот по ходу своего движения.
Автомобилисту следует не забывать перед маневром перестроиться в правый крайний ряд транспортного пути, иначе можно застрять среди потока машин, пока они все не разъедутся. В противном случае водитель ждет образования пустого «окна». Если место позволяет – необходимо быстро свернуть или попробовать занять позицию у края дороги для последующего свободного маневра.
Как повернуть налево и развернуться на перекрестке
Данный вид поворота заставляет паниковать начинающих водителей. Ведь такие дороги строятся без каких-либо регулирующих устройств. Все зависит от собранности, внимания и реакции водителя. Первым делом он показывает свое намерение совершить маневр с помощью нужного сигнала поворота — включается левый мигающий поворотник. Другие участники движения видят сообщение и корректируют свой маршрут. Далее автомобилисту следует перестроить машину ближе к центру дороги. При отсутствии помех (пешеходов, трамвая), остается только совершить поворот налево или развернуться.
Правила движения при проезде прямо
Маневр прост в выполнении, ведь человеку не нужно никуда сворачивать или перестраиваться, просто ехать прямо, при этом наблюдая за дорожной ситуацией. Если необходимо, подождать пока исчезнут все помехи. В данном случае автомобилисту следует придерживаться правила правой стороны. Уступить дорогу необходимо:
- автомобилям, поворачивающим вправо;
- движущимся по крайнему ряду проезжей части, но желающим повернуть влево;
- приближающийся машине из-за угла с включенным правым маячком.

Ответственность за определение способа езды по нерегулируемому перекрестку лежит на водителе транспортного средства. Автомобилист должен быть предельно внимательным и действовать по ситуации, так как на таких перекрестках возникает большое количество происшествий.
Круг не значит «круговое движение»!
У водителей Петербурга сегодня окончательно закружилась голова от нововведения в ПДД. Нарушения происходят один за другим, это естественно затрудняет общее передвижение транспорта по городу. А все потому что не все автолюбители поняли поправки неправильно.
Сегодня начали действовать поправки в правила дорожного движения, которые изменяют очередность проезда автомобилей на перекрестке с круговым движением. По новым правилам дорожного движения, на перекрёстке равнозначных дорог, на котором организовано круговое движение и который обозначен дорожным знаком 4. 3, водитель, въезжая на такой перекрёсток, обязан уступить дорогу транспортным средствам, движущимся по данному перекрёстку. Если на перекрёстке с круговым движением установлены знаки приоритета или светофор, то транспорт движется по нему в соответствии с их требованиями. Такая практика существует практически во всех европейских странах и доказала свою эффективность. Новые правила подготовили в МВД. По задумке ведомства, при такой организации проезда пропускная способность дорог должна вырасти. Раньше в разных регионах страны, а иногда даже в пределах одного города, схемы проезда перекрестков с круговым движением отличались друг от друга, что приводило к образованию заторов и ДТП.
3, водитель, въезжая на такой перекрёсток, обязан уступить дорогу транспортным средствам, движущимся по данному перекрёстку. Если на перекрёстке с круговым движением установлены знаки приоритета или светофор, то транспорт движется по нему в соответствии с их требованиями. Такая практика существует практически во всех европейских странах и доказала свою эффективность. Новые правила подготовили в МВД. По задумке ведомства, при такой организации проезда пропускная способность дорог должна вырасти. Раньше в разных регионах страны, а иногда даже в пределах одного города, схемы проезда перекрестков с круговым движением отличались друг от друга, что приводило к образованию заторов и ДТП.
Но вот на дорогах Петербурга сегодня коллапс. Дело в том, что водители стали заложниками собственной невнимательности. Из всего выше сказанного они четко выделили ,во-первых, понятие круг и решили, что все площади, которые имеют эту форму снабжены круговым движением. А это не так. Продолжит наш автоэксперт Дмитрий Попов:
« Народ не различает, что такое «круговое движение» и что такое « Круглая площадь». Сегодня сообщали о площади Конституции. Никакого кругового движения там нет. Она круглая, но движение не круговое. Точно также надо говорить и про пересечение Софийской улицы и улицы Славы и про Большевиков – Народная, Руставели – Науки, Белы Куны – Софийская. Это все площади круглые, но без кругового движения».
Сегодня сообщали о площади Конституции. Никакого кругового движения там нет. Она круглая, но движение не круговое. Точно также надо говорить и про пересечение Софийской улицы и улицы Славы и про Большевиков – Народная, Руставели – Науки, Белы Куны – Софийская. Это все площади круглые, но без кругового движения».
Всего в городе чуть больше 20-ти площадей, которые можно называть площадями с круговым движением. На некоторых из них произошли изменения. Точнее, только на тех, которые до сегодняшнего дня были площадями равнозначными перекрестками. Ведь постановление правительства вносит поправки в порядок разъезда на площадях с круговым движением, не затрагивая и не внося изменения в пункт правил 13.9. То есть все что касается перекрестков, на которых есть знаки приоритета, то мы едем исключительно по знакам. Таким образом изменения вносятся только в порядок движения где площадь равнозначный перекресток. К слову, таких площадей в нашем городе не так много, как нам бы хотелось. Наш автоэксперт приводит порядка 7-ми примеров.
Наш автоэксперт приводит порядка 7-ми примеров.
« Например, Гражданский проспект — Северный проспект. Есть приоритет движения по Гражданскому. Знаки установлены перед перекрестком. Водители должны руководствоваться этими знаками. Площадь Комсомольская – проспект Стачек, Корабельная — Краснопутиловская улицы. Здесь приоритет по проспекту Стачек установлен по знакам. На них и ориентируемся».
Также здесь можно вспомнить и загородные примеры. Например, круговое движение в Пушкине перед вокзалом. Там знаков приоритета нету, там стоит знак «круговое движение» . Соответственно , поправки здесь работают и преимуществом пользуется тот, кто на круге.
В завершении, еще раз отметим, что кто на круге, тот не всегда главный, а также круг — это всегда круговое движение. Следите за знаками, будьте бдительны и удачной дороги.
пересечение | Math Goodies
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами. Давайте посмотрим на взаимосвязь наборов, описанных в примере 1 ниже.
Давайте посмотрим на взаимосвязь наборов, описанных в примере 1 ниже.
Пример 1: Пусть X = {1, 2, 3} и пусть Y = {3, 4, 5}. Что общего у X и Y ?
Анализ: Нарисуем диаграмму Венна из двух перекрывающихся кругов. Общие для обоих наборов элементы будут размещены в средней части, где круги перекрываются.
Решение:
Пояснение: Круг слева представляет набор X , а круг справа представляет набор Y . Заштрихованная область посередине — это то, что у них общего. Это их пересечение. Пересечение наборов X и Y равно 3.
Диаграмма Венна в примере 1 позволяет легко увидеть, что число 3 является общим для обоих наборов. Таким образом, пересечение X и Y равно 3, и это записывается как:
X ∩ Y = {3}
| Определение: | Пересечение двух наборов, X и Y, — это набор элементов, общих для X и Y .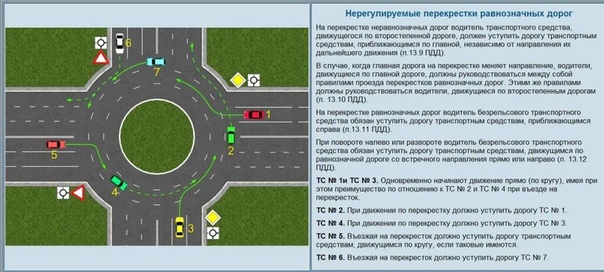 Он обозначается как X ∩ Y, и читается как « X пересекает Y ». Он обозначается как X ∩ Y, и читается как « X пересекает Y ». |
Таким образом, пересечение двух наборов — это набор элементов, общих для обоих наборов. Давайте рассмотрим еще несколько примеров пересечения.
Пример 2: Пусть = {подсчет чисел}, P = {число, кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение P и Q .
Анализ: Начните с заполнения элементов на пересечении. Поскольку P = {3, 6, 9, 12, 15, 18} и Q = {2, 4, 6, 8, 10, 12, 14, 16, 18}, мы знаем, что 6, 12 и 18 будут заполнены первыми.
Решение:
Обозначение: P ∩ Q = {6, 12, 18}
Другой способ определить пересечение двух множеств:
A ∩ B = {x | x A и x B }
Процедура построения пересечения двух множеств показана ниже.
Процедура построения пересечения двух наборов перекрывающихся наборов
Шаг 1:
Шаг 2:
Шаг 3:
Давайте посмотрим на пересечение других типов множеств. В примере 3 ниже, данные наборы не перекрываются.
Пример 3: Пусть = {животные}, A = {собаки} и B = {кошки}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение A и B .
Анализ: наборы A и B не перекрываются. Эти множества не пересекаются и не имеют общих элементов.
Решение:
Обозначение: A ∩ B = Ø
Два набора A и B не пересекаются, если их пересечение равно нулю. Это обозначается как A ∩ B = Ø , , где Ø — это нулевой или пустой набор .
Напомним, что универсальный набор — это набор всех рассматриваемых элементов, обозначенных заглавной буквой.Все остальные множества являются подмножествами универсального множества. Итак, в каждом приведенном выше примере кружки являются подмножествами универсального набора. Мы исследовали пересечение перекрывающихся множеств и непересекающихся множеств. Давайте посмотрим на пересечение одного набора, содержащегося в другом.
Пример 4: Пусть C = {a, r, e} и D = {f, a, i, r, e, s, t}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение множеств C и D.
Анализ: C — это подмножество D. Напомним, что это обозначается C D.
Решение:
Пояснение: Оказывается, C ∩ D = {a, r, e}, что равно множеству C.
В примере 4, поскольку C D , получаем, что C ∩ 902 925 Эти отношения определены ниже.
Процедура рисования пересечения одного набора, содержащегося в другом, показана ниже.
| Процедура построения пересечения одного набора, содержащегося в другом | |
| Шаг 1: | Нарисуйте один круг внутри другого. |
| Шаг 2: | Запишите элементы внутреннего круга. |
| Шаг 3: | Запишите оставшиеся элементы внешнего круга. |
Давайте посмотрим, сможете ли вы выполнить задачу, представленную в примере 5.
Пример 5: Учитывая диаграмму Венна ниже, назовите участника Band, который не входит в Band и Chorus.
Анализ: Эта проблема просит нас найти участника Band, который не находится на пересечении Band и Chorus.
Решение:
Пояснение: Сэм, Лорри и Рауль являются членами только группы. Кроме того, эти студенты не участвуют в оркестре и хоре.
Резюме: Пересечение двух множеств A и B, обозначенное A ∩ B, является набором элементов, общих как для A, так и для B.Формальное определение пересечения показано ниже.
A ∩ B = { x | x A и x B }
Упражнения
Указания: нарисуйте и обозначьте диаграмму Венна, чтобы помочь вам ответить на каждый из приведенных ниже вопросов. Выберите свой ответ, нажав соответствующую кнопку. Отзыв на ваш ответ представлен в БЛОКЕ РЕЗУЛЬТАТОВ. Если вы допустили ошибку, переосмыслите свой ответ, а затем выберите другую кнопку.
| 1. | Учитывая = {яблоки, апельсины, бананы, груши} и = {апельсины, груши, виноград}, что будет ∩ ? |
| 2. | Учитывая = {четные целые числа} и = {простые числа}, что будет ∩ ? |
| 3. | Учитывая = {13, 21, 34, 55, 89} и = {однозначные цифры}, что будет ∩ ? |
| 4. | Учитывая = {суббота, воскресенье} и = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, что такое ? |
| C ∩ D = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье} C ∩ D = {понедельник, вторник, среда, четверг, пятница} C ∩ D = {суббота, воскресенье} Все выше. ЯЩИК РЕЗУЛЬТАТОВ: |
| 5. | Учитывая приведенную ниже диаграмму Венна, что из следующего является элементом , а не элементом ( ∩ )? |
| | |
Пересечение наборов
Литература к занятию 5 — (продолжение)
Пересечение наборов
Перед продолжая читать эту сессию, вы можете просмотреть математические определения слов и и или , которые будут рассмотрены позже в этом сеансе.
Перекресток : Установленная операция перекресток принимает только элементы, которые есть в обоих наборах. Пересечение содержит элементы, которые два набора есть общее. В пересечение — это место, где два набора пересекаются.
В обозначении конструктора наборов: A ∩ B = { x ∈ U : х ∈ A и х ∈ B }.
Диаграмма Венна для A ∩ B показан справа где заштрихованная область представляет набор A ∩ Б. |
Пример: Позволять A = { a,
b, c, d } и B = { b,
д, д} .потом А ∩ В = { b,
d }.
Элементы b и d — единственные
элементы, которые есть в обоих наборах A и Б .
Пример: Позволять G = { т, a, n } и H = { n, a, t }.потом G ∩ H = { a, n, т }. Обратите внимание, что здесь G = H = G ∩ H .
Пример: Позволять C = {2, 6, 10, 14,…} и D = {2, 4, 6, 8, …}. Тогда C ∩ D = {2, 6, 10, 14,…} = С .
Пример: Почему место, где улица и перекресток проспекта, называемый перекресток ? Местоположение содержится как в улице, так и в проспект.
Пример: Позволять E = { d, a, y } и F = { n, i, g, h, t }. Затем E ∩ F = ∅.
Примечание: Во всех примерах пересечение — это подмножество каждого множества, образующего пересечение, то есть A ∩ В ⊆ A и А ∩ В ⊆ Б.
Непересекающиеся множества: Два набора, чьи пересечение — это пустое множество, называются непересекающихся множеств .
Пример: Позволять E = { d, a, y } и F = { n, i, g, h, t }. С E ∩ F = ∅ множества E и F — непересекающиеся множества.
Возврат
на домашнюю страницу Пейля | Миннесота
Государственный университет Мурхед | Математика
Отдел
Союз, пересечение и дополнение | Математика для гуманитарных наук
Обычно наборы взаимодействуют. Например, вы и ваш новый сосед по комнате решили устроить домашнюю вечеринку, и вы оба приглашаете свой круг друзей.На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Союз, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах).
Штуцер обозначен A ⋃ B.
Более формально, x ∊ A ⋃ B , если x ∊ A или x ∊ B (или оба)
Пересечение двух наборов содержит только элементы, которые есть в обоих наборах.
Перекресток обозначен A ⋂ B.
Более формально, x ∊ A ⋂ B , если x ∊ A и x ∊ B
Дополнение набора A содержит все, что равно , а не в наборе A .
Дополнение обозначается как A ’, или Ac , или иногда ~ A .
Пример 5
Рассмотрим наборы: A = {красный, зеленый, синий} B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
a) Найдите A ⋃ B
Объединение содержит все элементы в любом наборе: A ⋃ B = {красный, зеленый, синий, желтый, оранжевый}
Обратите внимание, мы указываем красный только один раз.
б) Найдите A ⋂ B
Пересечение содержит все элементы в обоих наборах: A ⋂ B = {красный}
c) Найдите Ac ⋂ C
Здесь мы ищем все элементы, которые являются , а не в наборе A , а также в C .
Ac ⋂ C = {оранжевый, желтый, фиолетовый}
Попробовать 2
Используя наборы из предыдущего примера, найдите A ⋃ C и Bc ⋂ A
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить Ac , поскольку все, от цвета фуксии до щенков и арахисового масла, включено в комплект.По этой причине дополнения обычно используются только на перекрестках или когда у нас есть универсальный набор.
Универсальный набор
Универсальный набор — это набор, который содержит все интересующие нас элементы. Это должно быть определено контекстом.
Дополнение относится к универсальному набору, поэтому Ac содержит все элементы универсального набора, которых нет в A .
Пример 6
а) Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
b) Если бы мы группировали ваших друзей на Facebook, универсальный набор был бы всеми вашими друзьями на Facebook.
c) Если вы работали с наборами чисел, универсальным набором мог бы быть все целые числа, все целые числа или все действительные числа
Пример 7
Предположим, что универсальным набором является U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то
Ac = {3, 5, 6, 7, 8, 9}.
Как мы видели ранее с выражением Ac ⋂ C , операции над множествами могут быть сгруппированы вместе.Символы группировки можно использовать так же, как и в арифметике, — для задания порядка операций.
Пример 8
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}
W = {утка, кролик, олень, лягушка, мышь}
a) Найдите ( H ⋂ F ) ⋃ W
Начинаем с пересечения: H ⋂ F = {собака, кролик}
Теперь объединяем полученный результат с W : ( H ⋂ F ) ⋃ W = {собака, утка, кролик, олень, лягушка, мышь}
b) Найдите H ⋂ ( F ⋃ W )
Начинаем с союза: F ⋃ W = {собака, корова, кролик, утка, свинья, олень, лягушка, мышь}
Теперь мы пересекаем этот результат с H : H ⋂ ( F ⋃ W ) = {собака, кролик, мышь}
c) Найти ( H ⋂ F ) c ⋂ W
Начинаем с пересечения: H ⋂ F = {собака, кролик}
Теперь мы хотим найти элементы W , которые равны , а не в H ⋂ F
( H ⋂ F ) c ⋂ W = {утка, олень, лягушка, мышь}
пересекающихся линий — пояснения и примеры
Теперь, когда вы изучаете геометрию или классы предварительного вычисления, вы несколько раз столкнетесь с концепцией пересекающихся линий .Вот почему нам нужно понимать концепции, связанные с пересекающимися линиями.
А пока давайте быстро перейдем к определению пересекающихся линий:
Пересекающиеся линии — это линии, которые пересекаются в одной точке.
Удивительно, как простое определение может помочь нам узнать важные свойства углов и систем линейных уравнений. Эта статья поможет нам понять определение, свойства и применение пересекающихся линий.
Определение пересекающихся линий
Пересекающиеся линии — это две или более линий, которые копланарны друг другу и встречаются в общей точке.
Три пары линий, показанные выше, являются примерами пересекающихся линий. Посмотрите, как каждая пара пересекается в точке $ \ boldsymbol {O} $? Мы называем это точкой пересечения . Сегменты линии также могут пересекаться и иметь точку пересечения.
Имейте в виду, что три или более линий могут иметь более одной точки пересечения.
Линии $ \ overline {WX} $, $ \ overline {YZ} $ и $ \ overline {UV} $ пересекаются друг с другом, и, как можно видеть, эти линии имеют три точки пересечения.
- Линии $ \ overline {WX} $ и $ \ overline {UV} $ пересекаются в точке $ \ boldsymbol {O} $.
- Прямые $ \ overline {YZ} $ и $ \ overline {UV} $ пересекаются в точке $ \ boldsymbol {N} $.
- Прямые $ \ overline {WX} $ и $ \ overline {YZ} $ пересекаются в точке $ \ boldsymbol {M} $.
Углы, образованные этими пересекающимися линиями (и линейными сегментами), обладают интересными свойствами, которые мы скоро узнаем в следующих нескольких разделах.
Какие реальные примеры пересекающихся линий?
Один из способов проверить наше понимание определения пересекающихся линий — это подумать о реальных примерах, представляющих пересекающиеся линии. Вы можете придумать что-нибудь? Вот три, которые помогут вам перечислить больше примеров:
- Наши ножницы — отличные примеры объектов, которые пересекаются друг с другом и имеют общую точку.
- Перекрестки также представляют собой пересекающиеся линии, поскольку они встречаются в точках пересечения.
- Линии этажей также пересекаются друг с другом и имеют общие точки пересечения.
Как использовать пересекающиеся линии в координатной геометрии?
Хотите узнать, что означает пересечение двух линий или кривых в координатной геометрии? Ниже приведены лишь некоторые из свойств, которые мы узнаем о пересекающихся линиях в системе координат xy.
- Когда два графика двух функций пересекаются друг с другом, точка пересечения представляет собой решение, когда обе функции приравниваются друг к другу.
- Это также означает, что при пересечении двух линий или графиков их уравнение будет иметь решение.
- Линии, которые пересекаются с осями $ x $ и $ y $, содержат точки пересечения и представляют собой точки пересечения $ x $ и $ y $ соответственно.
Мы узнаем больше обо всех этих основных концепциях, когда углубимся в функции и решим функции с помощью графиков.
А пока давайте рассмотрим общие свойства углов в точке пересечения.В следующих разделах мы также узнаем, как применять их при решении словесных задач, связанных с углами и пересекающимися линиями.
Свойства углов, образованных пересекающимися линиями
Когда две или более прямых пересекаются, они образуют разные углы в точке пересечения.
Линии $ \ overline {AB} $ и $ \ overline {CD} $, например, пересекаются в точке $ \ boldsymbol {O} $. Они также образуют четыре угла в точке пересечения: $ \ angle COA $, $ \ angle COB $, $ \ angle BOD $ и $ \ angle AOD $.
Вы также заметили две пары вертикальных углов? Если вам нужно напомнить, что такое вертикальные углы, вы можете ознакомиться с этой статьей о вертикальных углах, которую мы написали ранее. Для случая двух пересекающихся линий, показанных выше, у нас есть следующие вертикальные углы:
- $ \ angle COA $ и $ \ angle BOD $
- $ \ angle COB $ и $ \ angle AOD $
Свойства вертикальных и линейных углов по-прежнему применяются к углам, образованным двумя пересекающимися линиями.
Что происходит с углами, когда третья линия пересекает две пересекающиеся линии посередине?
Применяются те же свойства, и согласно постулату сложения углов угол, пересекаемый третьей пересекающейся линией, создаст два угла, которые в сумме составят величину пересеченного угла.
- Это означает, что сумма $ \ boldsymbol {\ angle SOW} $ и $ \ boldsymbol {\ angle WOU} $ равна $ \ boldsymbol {\ angle SOU} $.
- Аналогично $ \ boldsymbol {\ angle VOX + \ angle XOT = \ angle VOT} $.
Хотите проверить эти концепции? Вы можете попробовать построить четыре пересекающиеся линии и проверить, как ведут себя углы.
Теперь, когда мы узнали об определениях и свойствах пересекающихся линий, пришло время поработать над некоторыми вопросами, чтобы проверить свои знания.
Пример 1
Заполните следующие инструкции: иногда , никогда и всегда .
- Параллельные линии могут ____________ быть пересекающимися.
- Перпендикулярные линии могут ____________ быть пересекающимися линиями.
- Стрелки часов могут ____________ представлять две пересекающиеся линии.
- Пересекающиеся линии ______________ будут иметь более одной точки пересечения.
Решение
При работе с подобными вопросами всегда полезно вернуться к определению используемых терминов.
- Параллельные линии — это линии, которые никогда не пересекутся, поэтому никогда не встретятся.
- Перпендикулярные линии, с другой стороны, вместе образуют 90 °, поэтому они всегда будут .
- Стрелки часов пересекаются в общей точке. всегда представляет две пересекающиеся линии.
- Для трех или более пересекающихся линий они могут иногда иметь две или более пересекающихся точек.
Пример 2
Какое из следующих утверждений неверно?
- Три пересекающиеся линии могут иметь общую точку пересечения.
- Две пересекающиеся линии образуют две пары вертикальных углов.
- Две пересекающиеся линии образуют четыре пары вертикальных углов.
- Три пересекающиеся линии никогда не могут иметь четыре общие точки пересечения.
Решение
Давайте продолжим и рассмотрим каждое из приведенных утверждений.
- Три пересекающиеся линии могут пересекаться только в одной общей точке, поэтому утверждение верно.
- Когда две линии пересекаются, они образуют четыре угла. Каждая пара углов напротив друг друга — это вертикальные углы, так что это утверждение верно.
- Две пересекающиеся линии образуют только четыре угла и две пары вертикальных углов. Это утверждение неверно.
- Максимальное количество точек пересечения между тремя пересекающимися линиями — три, поэтому невозможно иметь четыре общие точки.Следовательно, четвертое утверждение верно.
Пример 3
Постройте линию, которая будет пересекать линию $ \ overline {AB} $. Обозначьте линию и точку пересечения, затем назовите четыре угла, образованные двумя пересекающимися линиями.
Решение
Постройте вторую линию, которая пересекает линию $ \ overline {AB} $. Ниже приведены три пары пересекающихся линий, которые помогут вам создать свою собственную пару пересекающихся линий.
В трех примерах мы назвали линию пересечения $ \ overline {CD} $ и точку пересечения Point $ O $.Ваше решение может отличаться от приведенного выше, но не беспокойтесь, все они хороши, если две линии пересекаются.
Четыре угла, образованные для пересекающихся прямых, — это $ \ angle AOC $, $ \ angle AOD $, $ \ angle COB $ и $ \ angle BOD $. Если вы пометите свои строки по-другому, вы получите другой ответ, нежели тот, который мы показали.
Как узнать, что ваш ответ правильный? Проверьте, есть ли в названии всех углов одинаковая буква посередине.
Пример 4
Невозможно создать четыре пересекающиеся линии , которые имеют только одну точку пересечения.
Докажите неверность утверждения, построив контрпример.
Решение
Постройте четыре пересекающиеся линии, где все пересекаются в одной общей точке.
Приведенный выше пример является одним из возможных контрпримеров для утверждения. Не стесняйтесь создавать свои собственные, чтобы показать, что утверждение не соответствует действительности.
Используйте изображение, показанное ниже, чтобы ответить на вопросы 5–7 .
Пример 5
Назовите две пары пересекающихся линий и соответствующие им точки пересечения.
Решение
Вот несколько пар линий, которые вы можете обнаружить на изображении, и мы включили их точки пересечения.
- Прямые $ \ overline {RS} $ и $ \ overline {TU} $ пересекаются в точке $ \ boldsymbol {A} $.
- Прямые $ \ overline {PQ} $ и $ \ overline {VW} $ пересекаются в точке $ \ boldsymbol {D} $.
- Прямые $ \ overline {PQ} $ и $ \ overline {TU} $ пересекаются в точке $ \ boldsymbol {B} $.
- Прямые $ \ overline {PQ} $ и $ \ overline {RS} $ пересекаются в точке $ \ boldsymbol {E} $.
- Прямые $ \ overline {VW} $ и $ \ overline {RS} $ пересекаются в точке $ \ boldsymbol {C} $.
Удалось ли вам найти две пары из списка, который у нас есть? Попытайтесь найти оставшиеся три, чтобы помочь вам освоить эту концепцию!
Пример 6
Назовите три отрезка прямой, которые имеют общую точку пересечения.
Решение
Помните, что отрезки линии также могут пересекаться. Вот два примера трех линейных сегментов, имеющих общую точку пересечения.
- Отрезки прямых $ \ overline {AC} $, $ \ overline {DC} $ и $ \ overline {EC} $ пересекаются в точке $ \ boldsymbol {C} $.
- Отрезки прямых $ \ overline {BD} $, $ \ overline {CD} $ и $ \ overline {ED} $ пересекаются в точке $ \ boldsymbol {D} $. {\ circ} $, каким будет значение $ \ angle RAT $?
Решение
Помните, что два вертикальных угла, образованные парой пересекающихся линий, встретятся в их общей точке пересечения.{\ circ} $, каков угол $ \ angle BOA $?
- $ \ angle AOC $ и $ \ angle BOD $
- $ \ angle AOB $ и $ \ angle COD $
- Определите, верны ли следующие утверждения. Если утверждение неверно, замените подчеркнутое слово, чтобы утверждение было правильным.
- Постройте линию, которая будет пересекать линию $ \ overline {XY} $. Обозначьте линию и точку пересечения, затем назовите четыре угла, образованные двумя пересекающимися линиями.
- Докажите, что утверждение неверно, построив контрпример. {\ circ} $, каким будет значение \ angle UCR $?
6.{\ circ} $, какова угловая мера $ \ angle MOP $?
Предыдущий урок | Главная страница | Следующий урок√ Интервалы (объединение и пересечение)
Определение
В математике интервал — это набор действительных чисел со свойством, что любое число, лежащее между двумя числами в наборе, также включается в набор.
Например, набор всех чисел x, удовлетворяющих 3 ≤ x ≤ 5, представляет собой интервал, содержащий 3, 5 и все числа между ними.
Интервал: все числа между двумя заданными числами.
Примеры
Интервал с 3 по 5 включает:
3,1
3,1111
3,5
4,75
4,80001
9/2
4,9937
от центрального числового вычисления до интервалов. метод, который автоматически обеспечивает гарантированные вложения для произвольных формул, даже при наличии неопределенностей, арифметических округлений и математических приближений.
Реальные интервалы играют важную роль в теории интегрирования. Это простейшие наборы, размер, меру или длину которых легко определить.
Затем понятие меры может быть расширено на более сложные наборы действительных чисел.
Неравенства, интервальная запись и числовая строка
Неравенства
Уравнения и неравенства — это математические предложения, образованные путем соотнесения двух выражений друг с другом. В уравнении 2 выражения считаются равными, что обозначается символом =.
Пример:
Уравнение 25
25
x равно y Где, как в неравенстве, два выражения не обязательно равны, что обозначается символами:>, <, ≤ или ≥.
Обозначение Правило 7
7
≥ больше или равно < меньше ≤ меньше или равно Уравнение или неравенство, которое содержит по крайней мере 1 переменную: позвонил на открытое предложение .
Интервальное обозначение
Символ Правило [] исключить конечное значение Интервал чисел между a и b, включая a и b, часто обозначается [a, b]. Эти 2 числа называются конечными точками интервала.
Числовая строка
все числа от 4 до 15, не включает 4, но включает 15
Примеры
Чтобы включить 0, но не включать 7:
Неравенства 0 ≤ x <7 Номерная строка Обозначение интервалов [0, 7) Открыто или закрыто
Чтобы указать, что одна из конечных точек должна быть исключена из set, соответствующую квадратную скобку можно заменить скобкой или перевернуть.Таким образом, в обозначении конструктора набора:
Интервальное обозначение Неравенства 9256 Детали ( a, b ) a an открытый , b )56 интервал
a ≤ x закрыто слева, открыто справа ( a, b ] a открыто слева, закрыто справа [ a, b ] a ≤ x ≤ b 9 0048 a закрытый интервал Примечание :
(a, a), [a, a) и (a, a] каждый представляет пустой набор, тогда как [a, a] обозначает набор {а}.Когда a> b, все 4 обозначения обычно используются для представления пустого набора.
До бесконечности (не дальше):
интервал может быть определен как подмножество расширенных действительных чисел, набор всех действительных чисел, увеличенных на + ∞ и -∞.
Интервальное обозначение Неравенства + x> a больше чем [ a, + ∞ ) x ≥ a больше или равно ( -∞, a ) x меньше чем ( -∞, a ] x ≤ a меньше или равно ( — ∞, ∞ ) — ∞ без ограничений все вышесказанное значимо и отчетливо.В частности, (−∞, + ∞) обозначает множество всех обычных действительных чисел, а [−∞, + ∞] обозначает расширенные действительные числа.
Union and Intersection
У нас может быть 2 (или более) интервала.
Учитывая 2 интервала, двумя основными отношениями между ними являются их объединение и их пересечение.
Отношение Символ Union A ⋃ B набор элементов, которые находятся в любом наборе Пересечение A 2 Union
Объединение 2 наборов — это новый набор, который содержит все элементы, которые входят по крайней мере в 1 из 2 наборов.Союз записывается как A∪B или «A или B».
Неравенства Обозначение интервала 56
56
900 или x> 7
( -∞, 4 ) ⋃ (7 , + ∞ ) x ≤ 2 или 902 902 25 x> 5 ( -∞, 2 ] ⋃ (5 , + ∞ ) x < 1 или x ≥ 8 —( ∞, 1 ) ⋃ [8 , + ∞ ) x ≤ 0 или x ≥ 9 ( -∞, 0 ] ⋃ [9 , + ∞ ) Пересечение
Пересечение 1 наборов — это новый набор, который содержит все элементы, которые есть в обоих наборах.Пересечение обозначается буквами A∩B или «A и B».
Неравенства Интервал Обозначение 56
56
56
x < 7 и x> 4 ( -∞, 7 ) ⋂ (4 , + ∞ (4 ) , 7)x ≤ 5 и x> 2 ( -∞, 5 ] ⋂ (2 , + ∞ ) (2, 5] x < 8 и x ≥ 1 ( -∞, 8 ) ⋂ [1 , + ∞ ) [1, 8) x ≤ 9 и x ≥ 0 ( -∞, 9 ] ⋂ [0 , + ∞ ) [0, 9] Узнать больше
Инъективная, сюръективная и биективная
Нотация Set-Builder
Преобразования функций
0002 Преобразования функций
0002 9162 9162 9226 Установить индекс
Определение пересечения Merriam-Webster
ин · тер · секция | \ ˌIn-tər-ˈsek-shən , особенно в смысле 1 ˈin-tər-ˌsek- \ 1 : место или район пересечения двух или более объектов (например, улиц).3а : набор элементов, общих для двух или более наборов особенно : набор точек, общих для двух геометрических конфигураций.
б : операция поиска пересечения двух или более множеств.
определение пересечения по The Free Dictionary
Если описать ряд одинаковых сфер с их центрами, расположенными в двух параллельных слоях; с центром каждой сферы на расстоянии радиуса x sqrt (2) или радиуса x 1.41421 (или на некотором меньшем расстоянии) от центров шести окружающих сфер в том же слое; и на одинаковом расстоянии от центров соседних сфер в другом и параллельном слое; тогда, если будут образованы плоскости пересечения между несколькими сферами в обоих слоях, получится двойной слой гексагональных призм, объединенных вместе пирамидальными основаниями, образованными из трех ромбов; а ромбы и стороны шестиугольных призм будут иметь все углы, идентичные лучшим измерениям, которые были сделаны для клеток пчелиного улья.Время от времени, очевидно на каждом перекрестке улиц, из кронштейнов, установленных в стенах, тускло брызгали масляные фонари, которые были немного выше человеческой головы. ЕГО ТОЧКА ПЕРЕСЕЧЕНИЯ, до которой еще не удавалось добраться ни одному путешественнику, — это самое сердце Африки. и именно туда теперь должны быть направлены все усилия. На пересечении двух широких проспектов Ваш Кор спустился с уровня улицы на одну из больших пневматических станций города. «Подойдя туда, он увидел слева от себя, месье» Стэнджерсон; он повернул направо, в сторону «сворачивающей» галереи — способом, который он заранее подготовил для полета, где на пересечении двух галерей он сразу увидел бы, как я объяснил, слева от него Фредерик Ларсан в конце «поворотной» галереи, а впереди — папа Жак в конце «правой» галереи.Они окружили меня на пересечении двух коридоров. Привязав две верхние мачты вместе и учитывая их неравную длину, в точке пересечения я прикрепил двойной блок главных гарднеров. Только однажды я увидел человека. , и это было на пересечении нашего перекрестка с широкой белой магистралью, которая пересекает каждый обрабатываемый район в продольном направлении в его точном центре. суматоха, овладела своей цепью на пересечении двух частей, пересекающих круг диаметрально и под прямым углом.Ее чистые красные губы наполовину улыбались; ее безмятежный и откровенный лоб периодически встревожился под ее мыслями, как зеркало под дыханием; и из-под ее длинных, опущенных черных ресниц ускользнул своего рода невыразимый свет, придававший ее профилю ту идеальную безмятежность, которую Рафаэль нашел в мистической точке пересечения девственности, материнства и божественности. Он выбрал своего лучшего коня, вскочил ему на спину, поскакал по улице Rue aux Herbes, выбрав не дорогу, по которой выбрал Фуке, а сам берег Луары, уверенный, что он выиграет десять минут на общем расстоянии, и на пересечении двух линий , придумал беглеца, который не мог подозревать, что его преследуют в том же направлении.
Решение
Постройте две пересекающиеся прямые с точкой пересечения $ \ boldsymbol {O} $.
Вы можете увидеть четыре угла, образованные в точке пересечения. Это следующие углы: $ \ angle AOC $, $ \ angle BOD $, $ \ angle AOB $ и $ \ angle COD $.
Обратите внимание на две пары вертикальных углов — каждая пара обращена друг напротив друга.
Это означает, что две пары вертикальных углов:
Поскольку $ \ angle AOC $ и $ \ angle BOD $ — вертикальные углы, их угловые меры равны.{\ circ} $.
При работе с пересекающимися линиями и связанными с ними проблемами со словами всегда возвращайтесь к его основному определению и свойствам. Попробуйте выполнить еще несколько практических задач ниже, чтобы еще больше закрепить свои знания о пересекающихся линиях.
Практические вопросы
Пересекающиеся линии никогда не могут иметь общую точку .
Две пересекающиеся линии могут иногда две точки пересечения.
Пересекающиеся линии — это некопланарных прямых, которые пересекаются в одной точке.
Две пересекающиеся линии могут образовывать две пары вертикальных углов.

 1, 2.3.1 – 2.3.7 или 5.1, по отношению к пересекаемой (примыкающей), или дорога с твердым покрытием (асфальто- и цементобетон, каменные материалы и тому подобное) по отношению к грунтовой, либо любая дорога по отношению к выездам с прилегающих территорий. Наличие на второстепенной дороге непосредственно перед перекрестком участка с покрытием не делает ее равной по значению с пересекаемой.
1, 2.3.1 – 2.3.7 или 5.1, по отношению к пересекаемой (примыкающей), или дорога с твердым покрытием (асфальто- и цементобетон, каменные материалы и тому подобное) по отношению к грунтовой, либо любая дорога по отношению к выездам с прилегающих территорий. Наличие на второстепенной дороге непосредственно перед перекрестком участка с покрытием не делает ее равной по значению с пересекаемой.