От чего зависит крутящий момент двигателя автомобиля

Традиционно мы привыкли оценивать ходовые характеристики автомобилей мощностью двигателя, выраженной в лошадиных силах либо киловаттах. Однако в обычном ритме движения двигатель не нагружается на полную мощность. Максимальная мощность, отражаемая в технических характеристиках двигателей автомобилей, достигается при оборотах около 4000 об./минуту в дизельных и около 6000 об./минуту для бензиновых авто.

В случаях, когда необходимо придать автомобилю заметное ускорение, например, во время обгона, мы часто встречаемся с ситуацией, когда не получаем реальной отдачи от движка даже максимально утопив педаль акселератора. Именно в таких случаях на приемистость двигателя в первую очередь влияет крутящий момент, а не его максимальная мощность.

Крутящий момент двигателя: формула расчета

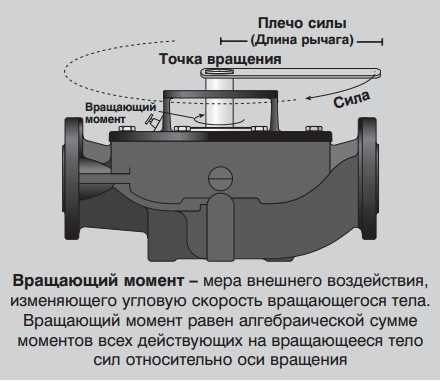
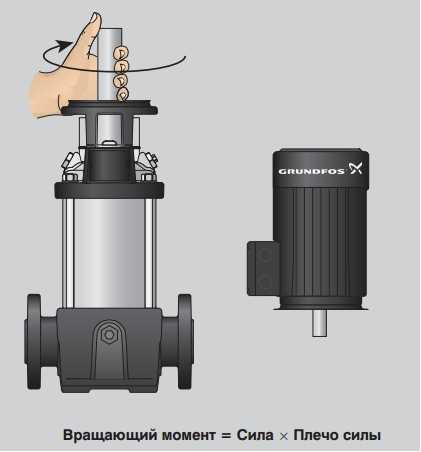
Согласно физическому определению крутящий момент М есть произведение силы F на длину плеча рычага L, куда эта сила приложена:

М = F * L

Сила F измеряется в ньютонах, длина  – в метрах. Таким образом, момент силы  —  в ньютон на метр.

Применительно к двигателям внутреннего сгорания  (ДВС) сила, выработанная в рабочем объеме  при сгорании топливно-воздушной смеси, давит на поршень, который передает свое усилие кривошипно-шатунному механизму коленвала. Именно длина рычага кривошипа учитывается при расчете крутящего момента. Именно он является определяющей характеристикой при оценке параметров динамического разгона автомобиля.

Видео — мощность и крутящий момент двигателя: что это такое с примерами

Максимальный крутящий момент двигателя в технических характеристиках всегда указывается совместно с величиной оборотов двигателя, при которых он может быть достигнут. В этом смысле различают низкооборотные и высокооборотные двигатели. К низкооборотным относятся, в большинстве, дизельные двигатели. Они могут «выстрелить» при движении с оборотами от 2000 до 3000 в минуту. Бензиновые двигатели обычно показывают максимальный крутящий момент при более высоких оборотах – от 4500 об./минуту.

Бензиновые высокооборотные двигатели достигают большой мощности за счет того, что им подвластны обороты до 8.000 об./минуту и более. Низкооборотные дизельные двигатели способны при меньшей мощности достигать максимальный крутящий момент на более малых оборотах (вплоть до 2.000), поэтому в динамике движения и обгона в городском ритме нисколько не уступают  бензиновым.

Для любителей математических вычислений полезна формула расчета мощности двигателя, исходя из его максимального крутящего момента:

Р = М * n / 9549 [килоВатт]

Здесь Р – мощность двигателя в килоВаттах, М – максимальный крутящий момент, n – количество оборотов двигателя.

Для перевода мощности Р в привычные лошадиные силы можно полученную величину умножить на 1,36.

Некоторые производители указывают величину номинального крутящего момента, определяемую на холостых оборотах двигателя.

Зависимости вращающего момента и мощности ДВС от частоты оборотов

В большинстве случаев зависимости величины крутящего момента и мощности двигателя от количества оборотов имеют такой вид, как на графике 1:

Из графика зависимости видно, что при малых оборотах крутящий момент небольшой, по мере их увеличения он достигает максимума 178 ньютон на метр при величине оборотов около 4500 в минуту, затем начинает падать. Вместе с тем мощность, пропорциональная произведению количества оборотов на крутящий момент до 5500 оборотов в минуту продолжает увеличиваться вплоть до 124 лошадиных сил, как на примере, затем после значительного уменьшения крутящего момента, также падает.

 

Физически это объяснить нетрудно. На малых оборотах в область сгорания в единицу времени поступает незначительное количество топливно-воздушной смеси, соответственно, сила, воздействующая на поршни, обеспечивающие крутящий момент, небольшие. При увеличении оборотов сгорание больше, крутящий момент увеличивается. Его уменьшение при дальнейшем увеличении оборотов связано с:

• увеличивающимися потерями мощности на трение механизмов двигателя;
• инерционными потерями;
• кислородным голоданием двигателя.

Современные двигатели с турбонаддувом обеспечивают поступление топливно-воздушной смеси в полном объеме и на малых оборотах, кроме этого имеют отлаженную систему электронного регулирования. За счет этого характеристика крутящего момента на различных оборотах более равномерная, как показано на графике 2:

Из графика видно, что высокий крутящий момент обеспечивается на низких оборотах вплоть до 2000 об./минуту и не сильно уменьшается до 5500 об./минуту.

Высокооборотные двигатели позволяют увеличить мощность за счет увеличения количества оборотов до 7.000 – 8.000 в минуту и более, как показано на графике 3:

Как видно из графиков, мощность двигателя является зависимой от крутящего момента и количества оборотов двигателя величиной. Приобретая автомобиль, желательно ознакомиться с динамическими характеристиками двигателя, зависимостью крутящего момента от величины оборотов.

Если вы желаете комфортно передвигаться в городском ритме движения, совершая уверенные обгоны и перестроения, лучше приобрести автомобиль с низкооборотным двигателем либо турбонаддувом. В том случае, если вы любитель погонять с ветерком на автобане, подходит вариант высокооборотного движка.

Видео — взаимосвязь мощности и вращающего момента ДВС:

Как его увеличить и в каких случаях это оправдано

Первоначально крутящий момент определяется на этапе конструкторской разработки двигателя внутреннего сгорания. Существенно увеличить эту характеристику можно, разве что при конструктивных изменениях ДВС. В практике специальных мастерских такой метод увеличения крутящего момента называется форсирование двигателя. Он заключается в увеличении компрессии за счет изменения геометрии поршневой группы, замене штатных форсунок, увеличения воздухозабора, других конструктивных решениях.

Более доступный способ увеличения крутящего момента – коррекция топливной карты с помощью чипования блока управления. Существенного увеличения крутящего момента (более 20%) при чиповании ожидать не следует, но такой метод менее дорогостоящий, не требует конструктивных изменений.

В любом случае, увеличение крутящего момента значительно уменьшает ресурс двигателя, так как все механические нагрузки на узлы двигателя рассчитаны, исходя из крутящего момента, определенного производителем. Их увеличение может вызвать преждевременный износ деталей.

Если вы пока не планируете участвовать на своем авто в соревнованиях по дрифтингу, дрэг-рейсингу и другим экстремальным видам автомобильных состязаний, лучше отложить идею увеличения крутящего момента до тех времен, когда участие в таких соревнованиях будет для вас реальной целью.

Читайте про то, как работает круиз-контроль на механике и какие особенности он имеет.

А в ЭТОЙ СТАТЬЕ узнаете как правильно демонтировать сигнализацию на машине.

Как восстановить работу https://voditeliauto.ru/poleznaya-informaciya/to-i-remont/obogreva-zadnego-stekla.html обогрева заднего стекла автомобиля.

Видео — что важнее мощность или крутящий момент:

Может заинтересовать:

Сканер для самостоятельной диагностики автомобиля

Добавить свою рекламу

Полис е-ОСАГО купить онлайн за 7 минут

Добавить свою рекламу

Как проверить Б/У авто перед покупкой

Добавить свою рекламу

Как быстро избавиться от царапин на кузове авто

Добавить свою рекламу

voditeliauto.ru

8 Расчет крутящих моментов на валах

8.1 Расчет крутящего момента на валу электродвигателя

Для определения крутящего момента на валу электродвигателя привода главного движения используется номинальная мощность и номинальная частота вращения:

где – мощность электродвигателя, кВт:

–номинальная частота вращения электродвигателя, мин^-1:

.

.

8.2 Расчет крутящего момента на валах привода

Крутящий момент на валах привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до соответствующего вала;

–расчетная частота вращения соответствующего вала, принимается по графику частот, мин^-1.

8.3 Расчет крутящего момента на первом валу привода

Крутящий момент на первом валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 1-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин

-1: = 2850 мин^-1.

КПД участка привода до первого вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

8.4 Расчет крутящего момента на втором валу привода

Крутящий момент на втором валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 2-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин^-1: = 630 мин^-1.

КПД участка привода до второго вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

— КПД зацепления зубчатых колес; .

8.5 Расчет крутящего момента на третьем валу привода

Крутящий момент на третьем валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 3-го вала;

–расчетная частота вращения на 1-ом валу, принимаем по графику частот, мин^-1: = 160 мин^-1.

КПД участка привода до третьего вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

— КПД зацепления зубчатых колес; .

8.6 Расчет крутящего момента на четвертом валу привода

Крутящий момент на четвертом валу привода рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до 4-го вала;

–расчетная частота вращения на 4-ом валу, определяется по формуле:

где – минимальная частота вращения четвертого вала, мин^-1:

мин^-1;

–максимальная частота вращения четвертого вала, мин^-1:

мин^-1.

КПД участка привода до четвертого вала рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

–КПД зацепления зубчатых колес; .

8.7 Расчет крутящего момента на шпинделе

Крутящий момент на шпинделе рассчитывается по формуле:

где – мощность электродвигателя, кВт:

–КПД участка привода от электродвигателя до шпинделя;

–расчетная частота вращения шпинделя, определяется по формуле:

где – минимальная частота вращения четвертого вала, мин^-1:

мин^-1;

–диапазон регулирования частот вращения шпинделя:

КПД участка привода до шпинделя рассчитывается по формуле:

где – КПД зубчатой муфты;

–КПД пары подшипников;

–КПД зацепления зубчатых колес; .

9 Проектный расчет передач

9.1 Расчет цилиндрической прямозубой постоянной передачиz₁–z₂

9.1.1 Исходные данные

1. Расчетный крутящий момент на первом валу привода, H·м:

Т₁ = 13 Н·м;

2. Число зубьев шестерни: z₁ = 18;

3. Число зубьев колеса: z₂ = 83;

4. Передаточное число передачи: u₁ = 4,76.

9.1.2 Выбор материала и термической обработки зубчатых колес

В качестве материала для зубчатых колес передачи выбираем сталь 40Х, которая отвечает необходимым техническим и эксплуатационным требованиям. В качестве термической обработки выбираем объемную закалку, позволяющую получить твердость зубьев 40..50HRC_э.

9.1.3 Проектный расчет постоянной прямозубой зубчатой передачи на контактную выносливость

Диаметр начальной окружности шестерни рассчитывается по формуле:

где вспомогательный коэффициент: для прямозубых передач

— расчётный крутящий момент на первом валу, Н·м: Т₁=13 Н·м;

коэффициент нагрузки для шестерни, равный 1,3..1,5: принимаем

— передаточное число:

отношение рабочей ширины венца передачи к начальному диаметру шестерни:

допускаемое контактное напряжение, МПа.

Допускаемое контактное напряжение для прямозубых передач рассчитывается по формуле:

где базовый предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений, МПа;

МПа;

S_H – коэффициент безопасности: S_H = 1,1.

Коэффициент отношения рабочей ширины венца передачи к начальному диаметру шестерни может приниматься в пределах

или определяется по формуле:

отношение рабочей ширины венца передачи к модулю: принимаем

число зубьев шестерни: z₁ = 18.

что находится в допустимых пределах .

Таким образом, диаметр начальной окружности шестерни равен:

Модуль постоянной прямозубой передачи определяется из условия расчета на контактную выносливость зубьев по рассчитанному значению диаметра начальной окружности шестерни по формуле:

где диаметр начальной окружности шестерни, мм:d_w1 = 38,75 мм;

число зубьев шестерни: z₁ = 18.

studfiles.net

Мощность момент — Энциклопедия журнала «За рулем»

Может ли бульдозер обогнать «формулу 1»? Может, но только на очень короткой дистанции

Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал. Крутящий момент может существовать и сам по себе, без мощности. Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.

Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F. Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.
Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того! Ракетчики, например, запрягают пламя напрямую, получают гигантские тяги и мощности, но о крутящих моментах вспоминают лишь в расчетах турбонасосных агрегатов, – да и то, если двигатели не твердотопливные!
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Итак, имеем дело с формулой (1). К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт.
На всякий случай напомним, что 1 лс = 75 кгм/сек = 75 • 9,81 Нм/сек = 735,75 Вт. Поэтому 107846 Вт ≈ 146,6 л.с.
А теперь прикинем мощность «формульного» двигателя с таким же скромным моментом, но при оборотах 18 тысяч! Результат – 880 л.с. (647 кВт), которые обеспечивают машине роскошную динамику. Никакого чуда нет: чем больше циклов совершит наш «моментик» за одну секунду, тем больше и совершенная им работа. Еще пример. В авиатехнике ныне практически господствуют газотрубинные двигатели. Повторив наш расчет для небольшого двигателя, с оборотами свободной турбины 40 тысяч в минуту, получим мощность около 1950 л.с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает!
Но вернемся к автомобилю. Как уже сказано, любому комфортней ездить на машине, у которой под капотом достаточно и мощности, и момента. Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость!
Гусеничному трактору дернуться и оборвать сцепку – плевое дело. Это похоже на выстрел из ружья – можно на миг и «формулу I» опередить. А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек². А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
Низшая передача бульдозера крайне «коротка»: чуть «перекрутил» – тяга упала. А другие не лучше, – вон и «формула» уже растворилась за горизонтом, так что для серьезных игрищ «мощи» на гусеницах маловато.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.

Рис. 1. Величины мощности N1 … N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.

Вся история современной транспортной техники – это непрерывная борьба за большие мощности. У наиболее знаменитых ракетоносителей они давно превысили 100 миллионов кВт. Это не ошибка — именно 100 000 000 000 Вт, или 100 ГигаВатт. И хотя притязания автомобилиста не столь велики, «прохватить» на динамичной машине всякий не прочь.
Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр.
(Желающие посчитать, могут воспользоваться следующими формулами. N_сопр. = N_w + N_f. Мощность аэродинамических потерь N_w для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м³, С_х = 0,3 и лобовой площади S = 2 • м² составляет: N_w = (0,3 • 2 • 1,25)/2 • v³ = 0,375 v³ Вт. А мощность шинных потерь N_f = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч N_сопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N₄ на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений N_сопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V₄ (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая N_сопр пересекла кривую N₄ возле вершины. Максимальные скорости на третьей и пятой передачах (V₃ и V₅) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность N_сопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт. Но придуманный нами автомобиль так ехать не может… Маловато мощи! Максимальная скорость снизится почти на 20 км/ч.

Рис. 2 — Так зависит крутящий момент (М1….М5) или тяговая сила (F_{тяг 1} …F_{тяг 5}) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (G_автом = 15000 н), может создать реальную тяговую силу не больше F_{макс. доп.} = 5250 Н.

На рис.2 величины крутящего момента М₁…М₅, а заодно и теоретические тяговые силы F₁…F₅ на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила F_тяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления φ = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.

Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов — оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?
А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: «Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать.» Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что «низовой», моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.

Проповедующие формулировку «скорость определяется мощностью, а динамика разгона — моментом двигателя» могут убедиться в своем заблуждении, решив простую задачу.
Вводные
1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить — чем с большей высоты упадет, тем сильней ударится).
2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.
Вопросы.
1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?
2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?

Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g^0.5.
Если ускорение определяется моментом — просто назовите цифру
Если ускорение определяется мощностью — тоже просто назовите цифру
Если цифру назвать не удается, значит параметр может быть самым разным и роли не играет.
Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной — для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт

Можно поступить и следующим образом.
Берите любой момент, который причина разгона, берите любой редуктор и разгоните тело 75 кг до скорости 3.13 м/c за 1 с.
Ограничение только по мощности — она не должна превышать 0.9 л.с.
Есть ли решение у этой задачи? Если нет — то почему?
Ответ.
Задача не имеет решения по той простой причине, потому что невозможно обеспечить заданную динамику — для нее не хватит мощности. Каким бы ни был момент.
Вывод. Момент двигателя для разгонной динамики не имеет значения, все решает мощность.

* Пояснение Вы поднимаете 75 кг получаете от этого энергию mgh. Она преобразуется так:
поскольку a = V² / 2h, а ускорение а у нас равно g, то V = (2hg)^0.5.
Кинетическая энергия тела E = mV²/2 = m2hg/2 = mgh.

Смотри также главу Как движется автомобиль

wiki.zr.ru

Расчет мощности и вращающего момента на валу двигателя

Для расчета мощности, кВт, и вращающего момента, Н·м, на валу двигателя следует пользоваться формулами:

вращательное движение
;
;

подъем груза

;

привод вентилятора

,

где κ — коэффициент, учитывающий действие противовеса;
v — скорость подъема груза, м/с;
Q — расход воздуха, м³/с;
р — давление на выходе вентилятора, Па;
g — ускорение свободного падения, м/с²;
η — КПД вентилятора, подъемника;
m — масса, кг;
n — частота вращения об/мин.

Полученные значения следует увеличить до ближайшего каталожного значения.

Двигатели эксплуатируются в самых разнообразных режимах.
Учет режима работы имеет большое значение при подборе двигателя. Мощности двигателей, указанные в каталогах, приведены для режима S1 и нормальных условий работы, кроме двигателей с повышенным скольжением.

Если двигатель работает в режиме S2 или SЗ, он нагревается меньше, чем в режиме S1, и поэтому он допускает большую мощность на валу. При работе в режиме S2 допустимая мощность может быть повышена на 50 % при длительности нагружения 10 мин, на 25 % — при длительности нагружения 30 мин, на 10% — при длительности нагружения 90 мин. Для режима SЗ рекомендуются двигатели с повышенным скольжением.

Подробнее, о номинальных данных электрических машин, здесь.

Источник: Кравчик А.Э. и др. Выбор и применение асинхронных двигателей.

Помощь студентам

electrichelp.ru

формула расчета, от чего зависит

Парадокс, но лишь немногие автолюбители ясно представляют принципиальную разницу между «лошадиными силами» и «ньютон-метрами», в которых измеряется крутящий момент. В обиходе определение крутящего момента двигателя напрямую связывают с динамикой разгона, а лошадиные силы с максимальной скорость. Если говорить уж совсем грубо, то формулировка вполне удовлетворительна, хоть и не объясняет всей сути физических процессов. Восполнить теоретические пробелы, а также получить наглядное представление о том, что такое крутящий момент двигателя, — вам поможет предоставленный ниже материал.

Момент вращения

Если выражаться языком физики, то понятие о вращающем моменте легко уяснить, зная принцип получения преимущества от использования рычага. Вычисляемые путем сложения приложенных на рычаг усилий (вес груза) к длине плеча (рычага) «ньютон-метры», показывают потенциальное количество выполняемой работы. В случае с ДВС вес груза – это усилие с которым поршень после сгорания топливно-воздушной смеси совершает возвратно-поступательное движение. Длина плеча будет не чем иным, как ходом поршня (расстояние от ВМТ до НМТ). Вращающее усилие создается только во время рабочего такта.

От чего зависит полка крутящего момента

Согласно расчетной формуле Мкр = F х L, где F – это сила, а L – длина плеча, момент вращения будет зависеть от КПД сгорания топливно-воздушной смеси (F) и величины хода поршней (L).

Поскольку автомобиль – это комплексный механизм, на крутящий момент двигателя влияет ряд характеристик других узлов и агрегатов. Ведущие колеса автомобиля будут получать максимальное тяговое усилие лишь в тот момент, когда взаимодействие механизмов является оптимальным. Пик крутящего момента достигается на таких оборотах двигателя, когда наполнение камеры сгорания рабочей смесью, сжигание продуктов горение и вывод отработавших газов осуществляется с минимальными механическими потерями. Для каждого двигателя этот параметр колеблется в зависимости от конструктивных особенностей и типа используемого топлива.

Мощность

Количество полезной работы, преобразованное возвратно-поступательными движениями КШМ, обозначается ньютон-метрами (крутящий момент). Тогда что такое мощность двигателя? Мощностью именуется количество произведенной работы за единицу времени. Иными словами, количество единиц крутящего момента, которое мотор способен выдать за определенный промежуток времени. Мощность двигателя измеряется в киловаттах (кВт).

Формула для расчета мощности в киловаттах:

P=Mkp*n/9549, где n – количество оборотов коленвала в минуту; Mkp – вращающий момент на коленчатом валу.

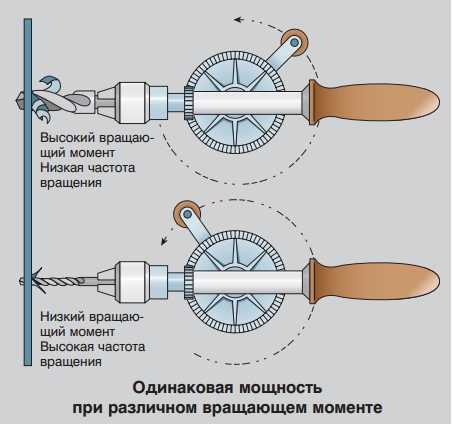
Нехитрое логическое умозаключение приводит нас к тому, что мощность мотора зависит от количества оборотов.

Соотношение крутящего момента к мощности

Для получения наглядного представления о взаимодействии двух величин рассмотрим основные характеристики мотора на графике. Он демонстрирует выдаваемую двигателем мощность и крутящий момент двигателя в зависимости от оборотов коленчатого вала.

График отчетливо демонстрирует тот факт, что тяговое усилие на колесах не прямо пропорционален количеству оборотов либо мощности. Двигатель достигает пика крутящего момента уже на 3 тыс. об/мин. Максимум мощности доступно на 5500 об/мин. В обоих случаях обороты продолжают расти, но отдача падает. Для обозначенного двигателя обороты от 2500 до 5 тыс. наиболее оптимальные.

В этом режиме работы близкая к максимальному значению «полка» момента позволит полноценно реализовать потенциал мотора на протяжении всего отрезка.

Приведенный график является примером гражданской настройки современных бензиновых моторов. Преимущества очевидны:

• стабильный прирост мощности;
• достаточно широкая «полка» с плавным приростом и затуханием.

Настройка подобного типа позволяет добиться «эластичности» двигателя. Такая работа обеспечивается не только программно (настройка ЭБУ), но и применением различных вспомогательных технологий (изменяемые фазы газораспределения).

Разница мощностных характеристик во многом зависит от конструкции системы впуска и выпуска. К примеру, двигатели оснащенные турбонаддувом в точке выхода на «буст» получают значительную прибавку в динамике. Крутящий момент и количество лошадиных сил таких моделей значительно превышают своих атмосферных собратьев.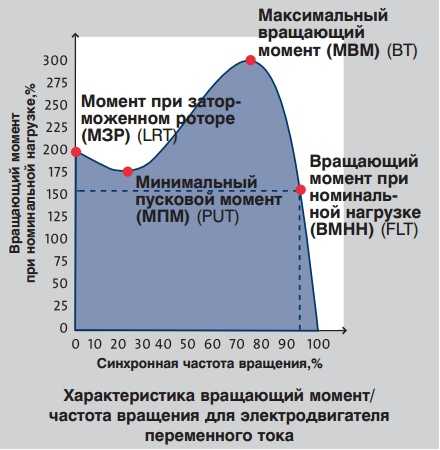

Что такое лошадиные силы

Наблюдательный читатель, скорей всего, отметит подозрительным тот факт, что до сих пор не прозвучало, всеми так любимое «лошадиные силы». Суть в том, что «скакуны» — это лишь дань моде тех времен, когда механизмам приходилось доказывать свое преимущество над живой рабочей силой. Поэтому превосходство (способность выполнить определенное количество работы) удобно было выражать в пересчете на потенциал одной лошади. Фактически 1 л.с – это усилие, которого достаточно для поднятия груза массою 75 кг на 1 м за 1 с.

Для того чтобы получить «лошадиные силы» достаточно умножить значение мощности в киловаттах на коэффициент 1,36.

Покупатели не потеряют ровным счетом ничего, если производители откажутся использовать «л.с» в качестве показателя мощностных характеристики автомобилей. Обозначить крутящий момент и мощность в кВт вполне достаточно. Но традиция настолько глубоко запечатлелась в сознании, что тратить усилия на ее разрушения попросту нецелесообразно.

Итоги

• Мощность мотора зависит от крутящего момента;
• «л.с» рассчитаны на достижение максимальной скорости. Автомобиль с большим количеством «скакунов» под капотом сможет развить внушительную скорость, но это займет очень много времени;
• от тягового усилия зависит насколько быстро двигатель сможет развить свою максимальную мощность;
• большое количество «ньютон-метров» позволяет более выгодно использовать потенциал двигателя. Такие моторы легче переносят нагрузки;
• чем шире «полка» момента, тем эластичней двигатель и приятней в управлении автомобиль;
• ввиду особенностей дизельных ДВС (большая степень сжатия, медленное горение смеси), а также применения современных систем дополнительного нагнетания воздуха, дизельные двигатели имеют больший крутящий момент с самих низких оборотов.

Выражаясь простым языком, «ньютон-метры» – это сила вашего автомобиля, а киловатты – выносливость.

autolirika.ru

Вращающий момент электродвигателя — Знаешь как

В двигателях постоянного тока вращающий момент определяется выражением М ≡ ФI_я, т.е. он пропорционален потоку и току якоря. В асинхронном двигателе момент создается вращающимся потоком Ф и током ротора I₂. Он может быть выражен

М ≡ ФI₂ cos Ψ₂.

Следовательно, момент пропорционален потоку и активной слагающей тока ротора I₂ cos Ψ₂, так как только активная слагающая тока определяет мощность, а значит и момент.

На рис. 10-20 представлена схема включения короткозамкнутого двигателя. Если пустить двигатель, включив рубильник 1, то в первый момент пуска, когда п₂ = 0, a s = 1, наведенная в роторе 2 э. д. с. Е₂ и пусковой ток I_2п максимальны. Однако, пусковой момент М_п не будет максимальным, а в 2—2,5 раза меньше максимального. Векторная диаграмма для цепи ротора (рис. 10-21), построенная подобно изображенной на рис. 9-9, показывает причину этого.

Рис 10-20. Схема включения короткозамкнутого асинхронного двигателя.

Обычно в роторе х₂ во много раз больше r₂ и угол Ψ₂, на который ток I_2п отстает от э. д. с. Е₂ велик. Поэтому активная слагающая тока I_2п cos Ψ₂, а значит и пусковой момент М_п малы. В современных асинхронных двигателях М_п/М_п = 1 — 1,5, хотя I_2п/ I_н≈ 4,5—6,5.

Это же явление по другому объясняется на рис. 10-19 и 10-22.

Рис. 10-21. Векторная диаграмма в цепи ротора. 

При описании принципа работы двигателя (рис. 10-19) было предположено, что ток I₂ совпадает по фазе с э. д. с. Е₂, т. е. что он активный (Ψ₂ = 0). На рис. 10-22 представлен момент пуска, когда направление э. д. с. в проводах ротора соответствует обозначенному на рис. 10-19, а ток показан отстающим от э. д. с. на угол Ψ₂. Тогда шесть проводов ротора (три под полюсом N и три под полюсом S) создают усилия, действующие в направлении вращения потока, а два провода вызывают противодействующие усилия. В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током I₂ и э. д. с. E₂.

Рис. 10-22. Ток в роторе двигателя в момент пуска.

По мере увеличения скорости вращения ротора реактивное сопротивление обмотки ротора x₂s = x₂s уменьшается, а вместе с этим уменьшается угол Ψ₂, так как сопротивление r₂ ≈ const. Наступает такое положение (рис 10-21), когда при некотором скольжении s_м ≈ 0,1—0,15 реактивное сопротивление x₂s становится равным активному r₂, угол Ψ — 45° и э. д. с. E_2s уравновешивает два равных падения напряжения I₂r₂ и I₂x_2s.В это время активная слагающая тока I₂ cos Ψ₂ и вращающий момент М_м становятся максимальными, несмотря на некоторое уменьшение тока I₂.

Обычно М_м/М_м = 1,8—2,5 и называется способностью к перегрузкe.

При дальнейшем разгоне ротора x_2s становится значительно меньшим, чем r₂, им можно пренебречь и считать ток ротора активным (I₂ ≈ I₂ cos Ψ₂). Так как E_2s = E₂s тоже продолжает уменьшаться, то вместе с током I₂ уменьшается и вращающий момент.

Максимальная скоростьn вращения будет при холостом ходе двигателя и тогда n₂ ≈ n₁ , a s ≈ 0. Зависимость вращающего момента от скольжения М = f (s) представлена на рис. 10-23.

Рис. 10-23. Зависимость вращающего момента двигателя от скольжения.

Нормальная работа двигателя возможна только на участке кривой при скольжениях s от нуля до s_м, так как в этом случае при увеличении тормозного момента и значит s вращающий момент возрастает. На участке от s = s_м до s = 1 работа двигателя неустойчива. Номинальный момент М_н соответствует обычно номинальному скольжению s_н = 1—6%.

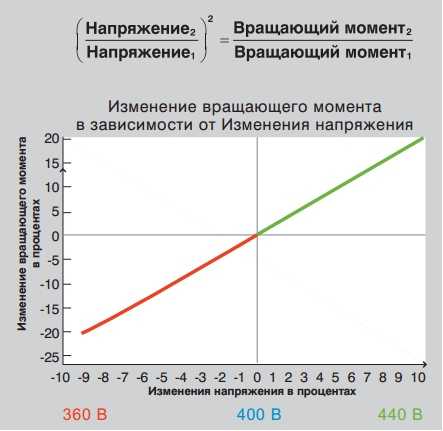
Поток Ф пропорционален напряжению U₁, подводимому к трансформатору. Сказанное остается в силе и для асинхронного двигателя. Так как М ≡ ФI₂ cos Ψ₂, то можно написать, что

I₂ cos Ψ₂ ≡ E_2s ≡ Ф ≡ U₁

Отсюда можно сделать очень важный для асинхронных двигателей вывод

M ≡ U₁U₁ ≡U²₁

т. е. вращающий момент пропорционален квадрату подведенного к статору напряжения. Таким образом, падение напряжения в сети, например до 0,9 U_1н, вызовет уменьшение момента до 0,9 • 0,9 М_н = 0,81 М_ни нагруженный двигатель может остановиться. Указанным обстоятельством и объясняется, частично, нормирование падения напряжения в распределительных сетях, питающих асинхронные двигатели.

В практике потребителя часто интересует механическая характеристика двигателя

п₂ = f (М) при U₁ = const и f₁ = const. Для удобства пользования по осям откладывают (n₂/n₁)100% и (М/М_н)100%.

Рис. 10-24. Механическая характеристика двигателя.

Эта характеристика получается простым перестроением рис, 10-23 и показана на рис. 10-24, где рабочая часть обозначена сплошной линией. Кривая 1 для двигателей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).

РАБОЧИЙ ПРОЦЕСС АСИНХРОННОГО ДВИГАТЕЛЯ

Трехфазный ток I₁протекая в трехфазной обмотке статора, создает н. F₁, вращающуюся со скоростью п₁= (f₁•60)/p (рис. 10-4, 10-5). Трехфазный ток ротора I₂ создает в трехфазной обмотке ротора н. с. F₂вращающуюся вокруг ротора со скоростью п₃ = (f₁•60)/p . Сам ротор вращается в сто-

рону н. с. со скоростью n₂. Тогда скорость вращения н. с F₂ относительно статора равна:

п₂ + п₃ = п₂ +(f₂ • 60)/p = n2 + (f₁s • 60)/p = n₂ + n₁s = n₂ + n₁((n₁ — n₂)/n₁) = n₁

Таким образом, обе н. с. F₁ и F₂ вращаются с одной скоростью n₁, друг относительно друга неподвижны и создают сообща вращающийся магнитный поток Ф. Следовательно, все приведенное на рис. 9-8 и 9-9 справедливо и для асинхронного двигателя.

Следует отметить, что благодаря воздушному зазору между ротором и статором ток холостого хода (рис. 9-7) двигателя очень велик (20—40)% I_1Н. Поэтому для улучшения cos φ₁ сети двигатель необходимо нагружать полностью.

 

Статья на тему Вращающий момент электродвигателя

znaesh-kak.com

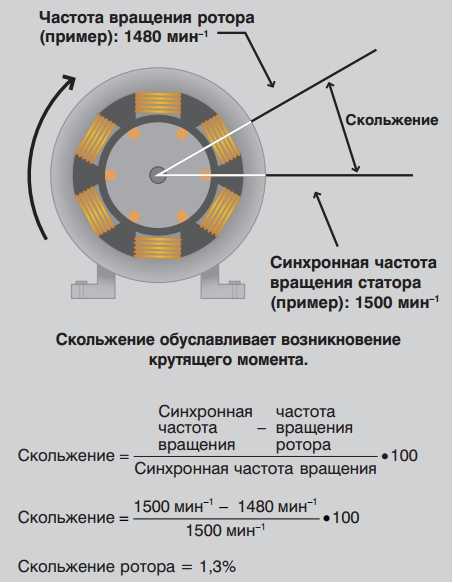
Выбор электродвигателя

Электродвигатель главная движущая сила электропривода. О том, какой электродвигатель выбрать для прямоходных механизмов рассказывается в этой статье

Вид электромеханизма	Тип двигателя в комплектации
ATL 10, BSA 10	АС 1-фазный, АС 3-х фазный, DS 24/12 B с тормозом и без
ATL 20-25-30-40 BSA 20-25-30-40	АС 1-фазный, АС 3-х фазный, DS 24/12 B с тормозом и без
ATL 50-63-80 BSA 50-63-80	АС 3-х фазный с тормозом и без
UAL 0 UBA 0	DS 24 B 12 B с тормозом и без
UAL 1-2-3-4 UBA 1-2-3-4	АС 1-фазный, АС 3-х фазный, DS 24/12 B с тормозом и без

Основные технических характеристики

Перед выбором электродвигателя важно понимать следующие физические характеристики:

Номинальная мощность — механическая мощность, измеряемая на валу, выражается в единицах измерения Ватт или КилоВатт. Однако в некоторой продукции мощность исчисляют лошадинными силами. 
Номинальное напряжение — напряжение, которое должно подаваться на клеммы электродвигателя, в соответсвии со спецификациями.

Статический крутящий момент (пусковой крутящий момент) — минимальный крутящий момент, который двигатель может обеспечить, с ротором при холостом ходе и при номинальной подаче напряжения частоты.

Промежуточный крутящий момент — минимальное значение крутящего момента, который развивается от питания двигателя с номинальным напряжением и частотой, от 0 об/мин до скорости, соответствующей максимальному крутящему моменту.

Максимальный крутящий момент — максимальный момент, который двигатель может развить во время эксплуатации с номинальной подачей напряжения и частоты.

Номинальный крутящий момент — крутящий момент соответствует номинальной мощности и номинальному количеству оборотов.

Номинальный крутящий момент рассчитывается по формуле:

Pn — номинальная мощность, кВт

n- номинальное количество оборотов, об/мин

Синхронная частота вращения, вычисляется по след. формуле:

f — подача частоты, Гц
р — количество пар полюсов

Диаграмма крутящих моментов

Условия эксплуатации

Влажность — электрооборудование должно эксплуатироваться при относительной влажности от 30% до 90% (без конденсации)

Необходимо исключить негативные последствия от случайного конденсата с помощью защищенного корпуса электрооборудования или, если необходимо, посредством дополнительных мер (например, встроенного нагревательного оборудования или системы кондицинирования, дренажных отверстий).

Высота и температура указаные в каталоге мощности предназначены для регулярного использования на высоте ниже 1000 м. над уровнем моря и при комнатной температуре от +5 оС до +40оС для двигателей с номинальной мощностью ниже 0,6 кВт, или при температуре от -15 оС до 40 оС для двигателей с номинальной мощностью, равной или превышающей 0,6 кВт. При других условиях эксплуатации (большей высоте и или температуре) значения изменяются в соответсвии с коэффициентом, указанным на графике.

Двигатели трехфазные или однофазные имеют направление движения по часовой стрелке. Против часовой — по запросу.

Напряжение — Частота: максимальное изменение подачи напряжения +/-10%. С этим допуском двигатели подают номинальную мощность. При долгосрочной эксплуатации с данными ограничениями возможно повышение температуры на 10 градусов С. Стандартная обмотка рассчитана на напряжение 230/400В и частоту 50 Гц. По запросу возможны другие значения напряжения частоты.
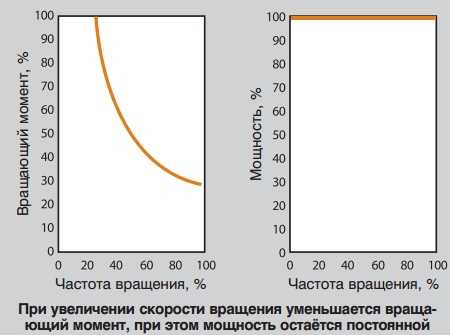
Частота вращения — крутящий момент: за исключением исполнения с четырьмя полюсами, двигатели имеют стандартное исполнение. Не рекомендуется использовать крутящие моменты выше номинального.

Обмотка статора выполняется из эмалированного медного провода (класс Н, 200 градусов), с измененными полиамидоэфирами полиамидами.
Класс изоляции F имеет пропитку полимерами, что обеспечивает высокую степень защиты от электростатического напряжения и механических нагрузок. Обмотка плотная, без воздушных мешков и с высокой степенью теплопередачи. Другие материалы из которых делается массовое производство обмоток имеют класс изоляции В, но по запросу мы ставим класс Н.

Двигатели тропического и морского исполнения: высокая степень защиты, которая используется для моторов, эксплуатирующихся в условиях тропического климата с высокой степенью влажности и неблагоприятных условиях эксплуатации обмотка покрывается слоем высококачественого глицерофталика, который имеет превосходные защитные характеристики.

Марка	Фото	Тип	Напряжение и частота	Диапазон габаритов и мощностей	Примечания
М		Асинхронные трехфазные электродвигатели общепромышленного исполенения	В/Гц: 230/400/50 +/- 10%В В/Гц: 266/460/60 +/- 10%В Об/мин.: 3000/1500/1000/750	Габарит, мм: 50-160 Мощность, кВт: 0,02-18,7	Размеры 71-160 адаптированы для использования с регулятором частоты. Вентилятор на валу, класс защиты IP 55F
DP		Асинхронные трехфазные многоскоростные электродвигатели	В/Гц: 400/50 +/- 10%В Об./мин.: 3000/1500, 1500/1000, 1500/750, 3000/1000, 3000/750, 1000/750, 3000/750	Габарит, мм: 63-160 Мощность, кВт: 0,06-18,7	Вентилятор на валу электродвигателя, класс защиты IP55F
MQ		Асинхронные трехфазные электродвигатели с квадратным кожухом	В/Гц: 230/400/50 +/- 10%В В/Гц: 266/460/60 +/- 10%В Об./мин.:1500	Габарит, мм: 63-90 Мощность, кВт: 0,18-1,5	Размеры 80-90 адаптированны для использования с регулятором частоты. Вентилятор на валу, класс защиты IP55F
MM		Асинхронные однофазные электродвигатели с встроенным конденсатором	В/Гц: 230/50 +/- 5%В Об/мин.: 3000/1500/1000	Габарит, мм: 50-100 Мощность, кВт: 0,045 — 2,2	Вентилятор на валу. Класс защиты IP55F. Поставка с встроенным или пристыкованным конденсатором.
MDC MDV		Асинхронные однофазные электродвигатели с центробежным выключателем с реле выключения подачи напряжения	В/Гц: 230/50 +/- 5%В Об./мин.:3000/1500/1000	Габарит, мм: 63-100 Мощность, кВт: 0,187 — 2,2	Принудительная вентиляция. Класс защиты IP55F. Поставка с встроенным или пристыкованным конденсатором. Центробежный выключатель. Встроенное реле подачи/отключения напряжения
MDE		Асинхронные однофазные электродвигатели с встроенным электронным реле	В/Гц: 230/50 +/- 5%В Об/мин: 3000/1500/1000	Габарит, мм: 63-100 Мощность, кВт: 0,187 — 2,2	Вентилятор на валу. Класс защиты IP55F. Поставка с встроенным или пристыкованным конденсатором.  Снабжены электронным пусковым реле.
МА		Асинхронные трехфазные электродвигатели с тормозом	В/Гц: 230/400/50 +/- 10%В В/Гц: 266/460/60 +/- 10%В Об/мин.: 3000/1500/1000/750	Габарит, мм: 55-160 Мощность, кВт: 0,02 — 18,7	Вентилятор на валу. Класс защиты IP55F. Класс защиты тормоза IP44, по запросу IP55. Возможна поставка с двойным тормозом и с ручным растормаживанием.
MADP		Асинхронные трехфазные многоскоростные электродвигатели с тормозом	В/Гц: 400/50 +/- 10%В Об./мин.: 3000/1500, 1500/1000, 1500/750, 3000/1000, 3000/750, 1000/750, 3000/500	Габарит, мм: 63-160 Мощность, кВт: 0,06 — 18,7	Вентилятор на валу. Класс защиты IP55F. Класс защиты тормоза IP44, по запросу IP55. Возможна поставка с двойным тормозом и с ручным растормаживанием.
MMA		Асинхронные однофазные электродвигатели с тормозом	В/Гц: 230/50 +/- 5%В Об/мин.: 3000/1500/1000	Габарит, мм: 50-100 Мощность, кВт: 0,09 — 2,2	Вентилятор на валу. Класс защиты IP55F. Класс защиты тормоза IP44, по запросу IP55. Возможна поставка с двойным тормозом и с ручным растормаживанием.
MADV MADC		Асинхронные однофазные электродвигатели с центробежным выключателем с реле выключения подачи напряжения с тормозом	В/Гц: 230/50 +/- 5%В Об/мин.: 3000/1500/1000	Габарит, мм: 63-100 Мощность, кВт: 0,187 — 2,2	Вентилятор на валу. Класс защиты IP55F. Класс защиты тормоза IP44, по запросу IP55. Возможна поставка с двойным тормозом и с ручным растормаживанием.
MADE		Ассинхронные однофазные электродвигатели с встроенным электронным реле с тормозом	В/Гц: 230/50 +/- 5%В Об/мин.: 3000/1500/1000	Габарит, мм: 63-122 Мощность, кВт: 0,187 — 2,2	Вентилятор на валу. Класс защиты IP55F. Класс защиты тормоза IP44, по запросу IP55. Возможна поставка с двойным тормозом и с ручным растормаживанием.
MV		Электродвигатели с векторным управлением (Серводвигатели)	Однофазная сеть: В/Гц: 230/50-60 +/-10% В Трехфазная сеть: В/Гц: 400/50-60 +/-10% В Об/мин.: 3000	Габарит, мм: 63 — 160 Момент, Н*м: 2,6 — 42	Сохранение момента при частоте вращения от 0 до максимальной. Высокая точность позиционирования. Программирование через пульт или компьютер
MVC MVS		Электродвигатели с встроенными энкодерами	Однофазная сеть: В/Гц: 230/50-60 +/-10% В Трехфазная сеть: В/Гц: 400/50-60 +/-10% В Об/мин.: 3000	Габарит, мм: 63 — 160 Момент, Н*м: 2,6 — 160	Сохранение момента при частоте вращения  от 0 до максимальной. Высокая точность позиционирования. Принудительная вентиляция
MII		Электродвигатели с встроенными регуляторами частоты вращения	Однофазная сеть: В/Гц: 230/50-60 +/- 10% В Трехфазная сеть: В/Гц: 400/50-60 +/-10% В Количество полюсов: 2/4/6	Габарит, мм: 71 — 112 Момент, кВт: 0,12 — 4	Недорогой вариант электродвигателя с частотным управлением. Принудительная вентиляция Встроенный тормоз, устройство тепловой защиты. Дистанционное управление.

 

 

 

Просмотров: 13891 | Дата публикации: Четверг, 13 июня 2013 05:41 |

www.servomh.ru