Пусковой момент электродвигателя

В процессе перехода механизма из состояния статики в состояние активности, на обмотки мотора начинает поступать номинальное напряжение, имеющее стандартную частоту. Именно тогда асинхронник может потребить наибольший объем энергии.

Под пусковым крутящим моментом мотора понимается момент его вращения в то время, как ротор остается статичным, а частота и напряжение переменного тока остаются номинальными. ПМ электромотора называется процесс развития повышенного вращающего момента.
Чтобы выявить показатель пускового момента, существует формула, которая предполагает использование кратности пм. Эта величина указывается в паспорте устройства. Чтобы определить величину пм асинхронника, нужно применить формулу:

Повышенных цифр на индикаторах пускового тока лучше не допускать в процессе запуска мотора, поскольку это может способствовать недостатку энергии, требующейся для корректной работы всех прочих систем и механизмов. Чтобы свести к минимуму значение тока пуска рационально применять пм по типу звезда и треугольник. Такие схемы более всего распространены при подключении электрических моторов.
Пусковой момент АЭД с фазным ротором обусловлен показателями по активному сопротивлению регулируемых резисторов, оказавшихся выведенными в роторную цепь. У асинхронников с короткозамкнутым ротором пусковой момент характеризуется наибольшим показателем. Но при этом существенно снижается показатель пускового тока.
Проверка электродвигателя по пусковому моменту проводится, учитывая динамическую нагрузку от маховых масс конструкции и дополнительного момента, который создается при помощи силы трения.
Короткозамкнутые асинхронные двигатели с повышенным пм имеют особенную конструкцию ротора. Эти свойства характерны для двигателей, имеющих двухклеточные и глубокопазные роторы.
Пусковой момент АЭД при уменьшении напряжения в 2 раза тоже уменьшается. Это подходит для конструкций, где произвести запуск можно с минимальной нагрузкой.

Что считать пусковым моментом

Многие задаются вопросом о том, как понимать кратность пускового момента АЭД. Ничего сложного здесь нет, поскольку сведения указываются в сертификате, паспорте или другом сопроводительном документе на электронный мотор. Под пусковым моментом понимается вращающий момент, который инициируется механическим способом. Его развивает мотор на валу непосредственно при запуске аккурат в то время, когда ток проходит через двигатель.
Иными словами, ПМ – вращающий момент, проявляющийся на валу, когда ток имеет устоявшееся значение, а скорость вращения нулевая, а обмотки электродвигателя имеют номинальное по частоте и напряжению значение.

Способы определения пускового момента

Чтобы узнать, как определить максимальный пусковой момент АЭД, потребуется воспользоваться специальной формулой:

Она помогает понять, за счет чего удастся повысить показатель. Стоит сказать о том, что пусковой момент обусловлен напряжением, которое подводится к обмотке статора. Чем оно ниже, тем дольше запускается двигатель и, соответственно, пусковой ток увеличивается, как и рабочий.

Расчет пускового момента

Он определяется по определенной формуле. Величина кратности может варьироваться в промежутке от 1.5 до 6. Важно соблюдать правило, в соответствии с которым статический момент всегда должен оказываться меньше пускового. Без этого невозможно добиться корректной работы мотора.
Чтобы понять, как определяется кратность ПМ асинхронника, нужно разобраться в самом механизме работы устройства. Непосредственно при запуске электрический мотор будет потреблять пусковой ток, показатель его существенно выше, чем у рабочего. Именно величина, которая обозначает разницу между указанными токами, обозначается как кратность, ее принято учитывать, как коэффициент. Но номинальный и рабочий токи – это разные обозначения, которые не стоит путать. Кратность тока обусловлена мощностью мотора. Если мощность невелика, то пусковой ток высокий.
Как определить пусковой момент электродвигателя и как определить пусковой момент асинхронного двигателя? Существует формула пусковой момент АЭД для расчета. Можно воспользоваться методом электрических измерений или воспользоваться специальными таблицами.

Увеличение пускового момента

Пусковой момент удастся увеличить за счет частотного преобразователя. Если сменить показатель сопротивления пускового реостата, удастся достичь большего пускового момента.
Но что произойдет, если уменьшить напряжение пускового момента вдвое? Он резко упадет. Изменение первичного тока определяется загрузкой электрического двигателя. При большой нагрузке асинхронного двигателя уменьшение напряжения на его зажимах приводит к перегрузке обмоток двигателя токами со всеми вытекающими отсюда последствиями. Наоборот, пусковой момент асинхронного двигателя при введении реостата в фазный ротор увеличивается.
Существуют правила, в соответствии с которыми должен проводиться запуск асинхронного электродвигателя. При каком способе пуска увеличивается пусковой момент асинхронного двигателя? Соединение ротора с реостатом во время включения подойдет для включения в работу моторов с разным ротором.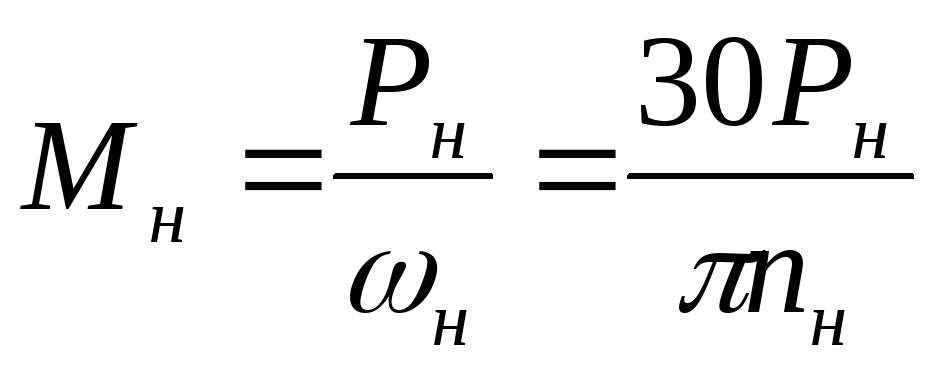 Если в цепь входит реостат, то уровень сопротивления увеличивается. Это обеспечивает увеличение пускового момента.
Асинхронные моторы, обладающие повышенным пусковым моментом созданы специально для приводов механизмов, характеризующихся высокими нагрузками на момент запуска. А вот моторы с повышенным показателем скольжения используют для оборудования, имеющего неравномерные ударные характеристики нагрузки и высокую частоту запусков и реверсов.
Как повысить пусковой момент? Нужно использовать АЭД с высоким ПМ. Его дальнейшее увеличение можно произвести, если использовать двигатели с обмоткой ротора по типу двойной «беличьей клетки», паз обязательно должен быть глубоким. У такого АЭД на роторе будет присутствовать пара короткозамкнутых обмоток. Одна из них пусковая, а другая рабочая. Чтобы повысить ПМ обмотка для запуска должна обладать большим активным сопротивлением, нежели рабочая.

Вычисление пускового момента однофазного АЭД при включенной и отключенной обмотке

ПМ для ротора однофазного мотора соответствует нулю, потому что одна обмотка создает два одинаковых по амплитуде магнитных поля только противоположных по направлению, и сумма их векторов будет равна 0.
Пусковым моментом однофазного АЭД называется вращающий момент, развивающийся на валу АЭД, когда ротор статичен, а статор тока закреплен на обмотках.
Ключевыми элементами каждого асинхронника можно по праву считать ротор (вращающийся элемент) и статор (неподвижная часть). За счет статора обеспечивается магнитное поле для вращения ротора.
ПМ однофазного АЭД без пусковой обмотки соответствует 1/2 максимального момента.

ДИНАМИЧЕСКИЙ РАСЧЕТ ДВИГАТЕЛЯ

Динамический расчёт кривошипно-шатунного механизма заключается в определении суммарных сил и моментов, возникающих от давления газов и от сил инерции. По этим силам производятся расчёты основных деталей на прочность и износ, а также определение неравномерности крутящего момента и степени неравномерности хода двигателя. Во время работы двигателя на детали кривошипно-шатунного механизма действуют: силы от давления газов в цилиндре; силы инерции возвратно-поступательно движущихся масс; центробежные силы; силы от давления на поршень со стороны картера и силы тяжести. В течение каждого рабочего цикла силы, действующие в кривошипно-шатун­ном механизме, непрерывно изменяются по величине и направлению. Поэтому для определения характера изменения этих сил по углу поворота коленчатого вала их величины определяют для ряда отдельных положений вала.

Исходные данные для динамического расчёта двигателя:

Диаметр цилиндра D = 0,12 м.

Ход поршня S = 0,14 м.

Длина шатуна L = 0,25 м.

Частота вращения коленчатого вала двигателя n = 1500 мин^-1.

Масса поршневого комплекта m_П. = 3,1 кг.

Масса шатуна в сборе m_L. = 4,3 кг.

Безразмерная координата центра масс шатуна L_B/L = 0,32.

Наружный диаметр шатунной шейки d = 0,078 м.

Диаметр полости в шатунной шейке d₁ = 0,031 м.

Длина шатунной шейки с = 0,051 м.

Плотность материала коленчатого вала ρ = 7,8∙10³.

Ширина щеки h = 0,15 м.

Высота щеки Н = 0,175 м.

Безразмерная координата центра масс щеки Х_Щ./R = 0,5.

Толщина противовеса b = 0,0285 м.

Вспомогательные расчёты двигателя

Площадь поршня, м²                

Радиус кривошипа, м                                          

Кинематический коэффициент                                       

Угловая частота вращения коленчатого вала, с^-1                                   

Прямолинейно движущаяся масса в цилиндре двигателя, кг                           

Вращающаяся масса шатуна в отсеке двигателя, кг                  

Масса шатунной шейки, приведенная к её оси, кг        

Масса щеки, приведенная к оси шатунной шейки, кг

Приведенная масса кривошипа, кг

Вращающаяся масса в отсеке двигателя, кг

Сила инерции вращающейся массы, кН

Расчёт сил и крутящего момента в отсеке двигателя

Сила давления газов, кН

где р – текущее значение давления газов в цилиндре, МПа.

Значение р выбирается для текущего значения угла поворота кривошипа
из расчёта рабочего процесса  (табл. А.1).

Ускорение прямолинейно движущейся массы, м/с²

где α – угол поворота кривошипа, градусы.

Сила инерции прямолинейно движущейся массы, кН

Суммарная сила, действующая в точке сочленения поршня с шатуном, кН

Нормальная сила, передаваемая поршнем на стенку цилиндра, кН

где β – угол отклонения шатуна от вертикали, градусы

Сила, передаваемая по шатуну на кривошип, кН

Радиальная составляющая силы Q_A на кривошипе, кН

Полная радиальная сила в отсеке, кН

Тангенциальная составляющая силы Q_A на кривошипе, кН

Крутящий момент на кривошипе, кН∙м

Расчёт сил и крутящего момента в отсеке двигателя на интервале углов поворота кривошипа от нуля до 710º с шагом Δα = 10º приведен в таблице 4.1. На рисунках 4.1 и 4.2 изображены графики зависимостей рассчитанных сил от угла поворота кривошипа.

Для наглядности, зависимости крутящего момента на кривошипе и общего крутящего момента, рассчитываемого ниже, от угла поворота кривошипа, изображены на одном графике (рис. 4.3).

Расчёт крутящих моментов, передаваемых коренными шейками

Чтобы результаты расчёта были максимально наглядными, необходимо предварительно пронумеровать элементы коленчатого вала. Будем нумеровать кривошипы начиная от носка коленчатого вала одним числом. Коренные шейки будут соответственно нумероваться двумя числами, обозначающими номера кривошипов, с которыми соседствует данная коренная шейка. С носка коленчатого вала происходит отбор мощности для привода вспомогательных агрегатов двигателя и генератора. В общем случае, крутящий момент, возникающий при этом, необходимо учитывать в расчётах. Однако в данном случае, так как двигатель предназначен для установки с генератором, этот крутящий момент будет составлять менее 5 % от индикаторного момента на валу двигателя. Поэтому в дальнейших расчётах крутящий момент на носке коленчатого вала не учитываем.

Крутящий момент М_1,2 на коренной шейке 1,2 равен моменту М₁, создаваемому на первом кривошипе. Крутящие моменты на каждой последующей коренной шейке складываются из момента на предыдущей коренной шейке и момента на предыдущем кривошипе. То есть, М_2,3 = М_1,2 +М₂; М_3,4 = М_2,3 + М₃ и так далее. Крутящий момент на последней коренной шейке равен общему крутящему моменту М_Кр., создаваемому двигателем.

Крутящий момент, создаваемый на данном кривошипе, зависит от угла поворота кривошипа. При заданном порядке работы цилиндров двигателя (1-3-4-2), каждый последующий цилиндр из порядка работы цилиндров будет отставать от предыдущего на 180º. Принимаем, что угол поворота первого кривошипа равен нулю (для четырёхтактного двигателя это всё равно, что 720º, так как весь его цикл длится два оборота коленчатого вала). Значения крутящегомомента при известном угле поворота кривошипа выбираются из таблицы 4.

1.

Все полученные величины крутящих моментов на любом кривошипе для углов поворота кривошипа от нуля до 710º с шагом Δα = 10ºсведены в таблицу 4.2. По рассчитанным значениям строится график зависимости общего крутящего момента, создаваемого двигателем, от угла поворота коленчатого вала, представленный на рисунке 4.3. На этом графике также нанесена величина среднего крутящего момента М_Кр.Ср., определяемая как среднее арифметическое значений крутящего момента на всём интервале углов поворота коленчатого вала.

Расчёт нагрузок на шатунные шейки и подшипники

В однорядном двигателе шатунная шейка нагружена силой Q_A, передаваемой по шатуну, и силой инерции P_B.L. вращающейся массы шатуна. Для удобства расчётов, силу Q_A заменяют двумя силами – Z_A, направленной к центру вращения кривошипа, и T_A, направленной под углом
 90º к Z_A в сторону вращения кривошипа     (рис. 4. 4).Шатунный подшипник нагружен реакциями шатунной шейки (рис. 4.5).

При расчёте нагрузки на шатунную шейку, К_Ш., используют систему коодинат Z_Ш.– Т_Ш., вращающуюся вместе с коленчатым валом. А составляющие реакции при расчёте нагрузки на подшипник, R_Ш., определяют в системе координат R_Z.Ш.– R_Т.Ш., жёстко связанной с шатуном (см. рис.  4.5).

Радиальная составляющая нагрузки на шатунную шейку, кН

Тангенциальная составляющая нагрузки на шатунную шейку, кН

Полная нагрузка на шатунную шейку, кН

Полученные значения нагрузок Z_Ш. и Т_Ш. можно использовать для определения нагрузок на шатунный подшипник. Составляющие нагрузок, кН

Полная нагрузка на шатунный подшипник, кН

Значения Z_Aи Т_Апри заданном угле поворота кривошипа выбирают из таблицы  .

1. Все расчёты по пункту  .5 для углов поворота кривошипа от нуля до 710º с шагом Δα = 10º представлены в таблице  .3.

Также по результатам данного расчёта построены годографы нагрузок на шатунную шейку и шатунный подшипник. Они изображены соответственно на рисунках  6. и  7.

Оценка неравномерности вращения коленчатого вала

Избыточная работа суммарного крутящего момента двигателя определяется как площадь наибольшей фигуры, образованного кривыми общего крутящего момента двигателя, М_Кр., и среднего крутящего момента, М_Кр.Ср.(рис. 4.3), с учётом масштаба графика. Она равна L_изб= 94,5 кН∙м.

Момент инерции вращающихся масс кривошипно-шатунного механизма в одном отсеке

_кшм==

где Z_{П  –} число противовесов, приходящихся в среднем на один кривошип.

Момент инерции обода маховика

где  — плотность материала маховика, кг/м³;

b – ширина маховика, м;

r₂ – внешний радиус обода маховика, м;

r₁ – внутренний радиус обода маховика, м.

Момент инерции ступицы маховика

где    b₁ – ширина ступицы маховика, м;

r₀ – радиус ступицы маховика.

Момент инерции маховика

Момент инерции вращающихся масс кривошипно-шатунного механизма

Степень неравномерности вращения коленчатого вала

Неравномерность вращения коленчатого вала должна составлять для дизель-генератора
 

Требования к инерции, мощности и крутящему моменту

Назад в отдел новостей

16 февраля 2023 г.

Manoj Pujari

Различные производители двигателей предоставляют онлайн-инструменты и калькуляторы, чтобы помочь пользователям выбрать идеальный миниатюрный двигатель, включая наше собственное приложение MotionCompass™, веб-приложение, предназначенное для предоставления решений для мини-двигателей, основанных на уникальных требованиях к движению для различных приложений.

Однако эти инструменты не должны заменять фундаментальное понимание факторов, влияющих на процесс выбора двигателя! Причина проста: выбор миниатюрного двигателя предполагает всестороннее знание конкретных параметров приложения, понимание факторов, которым приложение отдает приоритет, и техническое понимание вариантов решения движения, которые лучше всего подходят для удовлетворения этих требований.

Давайте рассмотрим два ключевых фактора выбора двигателя, соответствие инерции и требования к крутящему моменту/мощности, которые помогут проиллюстрировать важность понимания этих концепций, одновременно позволяя пользователям оценить и лучше использовать онлайн-инструменты для построения своих первоначальных расчетов.

Что такое согласование инерции?

Вращательная инерция — это свойство тела или системы, которое говорит нам, насколько что-то будет сопротивляться угловому ускорению, ускорению или замедлению вращения. Если система имеет большую инерцию вращения, будет трудно заставить ее ускоряться; если система имеет меньшую инерцию вращения, то заставить ее ускоряться должно быть относительно легко.

Согласование инерции относится к согласованию инерции нагрузки и инерции двигателя. Низкое отношение нагрузки к моменту инерции двигателя особенно желательно в приложениях, требующих либо высокого ускорения и замедления, либо чрезвычайно точного позиционирования для достижения желаемой производительности. Примеры применения, такие как высокоскоростная, высокоточная сборка и установка двигателей для текстильных нитеводителей, потребуют, чтобы двигатель работал в замкнутой системе с обратной связью. Теоретически желателен коэффициент инерции, близкий к 1. Однако в реальных приложениях это может быть недостижимо (и нецелесообразно). На самом деле, стремление к коэффициенту инерции, близкому к 1, может привести к увеличению размеров компонентов, повышению стоимости системы и повышенному энергопотреблению.

Неблагоприятные последствия несоответствия инерции или высокой нагрузки к инерции двигателя могут усугубляться «отсутствием жесткости» (податливости нагрузки) в системе, что приводит к увеличению времени отклика, снижению пропускной способности системы и резонансу. Это означает, что в требовательных приложениях рекомендуется начинать с возможности системы прямого привода, сводить количество элементов передачи мощности к минимуму и проектировать жесткие машины/муфты. Чтобы противодействовать влиянию податливости нагрузки и высокой нагрузки на инерцию двигателя, можно использовать следующие методы:

•	Редуктор. Использование редуктора уменьшит инерцию нагрузки в 2 раза по сравнению с передаточным числом.
•	Жесткая муфта/жесткая система/жесткая машина. Их использование поможет свести соответствие нагрузки к минимуму.
•	Настройка сервопривода. Проблема несоответствия инерции может быть смягчена за счет широкого использования современных систем управления благодаря их быстрым процессорам, использующим усовершенствованные алгоритмы управления в сочетании с устройствами обратной связи с высоким разрешением

А.

Прямой привод. При прямом приводе двигатель напрямую связан с нагрузкой (рис. 1). Используя вышеприведенное объяснение инерции вращения, давайте применим второй закон Ньютона в терминах вращения: T = Iα. Это фундаментальное уравнение показывает нам, что чем меньше инерция у системы, тем меньший крутящий момент потребуется для достижения желаемой скорости ускорения. Рис. 1. Двигатель с прямым приводом Если мы рассмотрим крутящий момент, необходимый для ускорения вала двигателя (T + I Mo = I + I M x α + I M ), и крутящий момент, необходимый для ускорения нагрузки (T + I L = I + I L x α + I L )), мы понимаем, что вал двигателя и нагрузка будут иметь одинаковое угловое ускорение и одинаковую угловую скорость для системы прямого привода с абсолютно жесткой муфтой, соединяющей двигатель с нагрузка (α + I M = α + I L = α & ω + I M = ω + I L = ω). Это означает, что мощность, необходимая для ускорения системы в целом, может быть найдена с помощью следующего уравнения: P = (IM+IL) x α x ω (уравнение 1). Эта мощность создается крутящим моментом двигателя (TM) и, следовательно, мощностью P = TM x ω (уравнение 2). Приравнивая уравнения 1 и 2, получаем момент двигателя, или момент, необходимый для разгона системы в целом: T + I M = (I + I M + I + I L ) x α ( Уравнение 3). Обратите внимание, что крутящий момент, необходимый для получения заданного ускорения, будет минимальным, если I + I M = I + I L . Таким образом, для максимальной передачи мощности инерция вращательной нагрузки должна быть близка к инерции двигателя.

Б.

Косвенный привод. Непрямой привод — это когда двигатель не связан напрямую с нагрузкой, а связан через один или несколько элементов передачи мощности, таких как шестерни, системы ременных шкивов, цепные приводы или шарико-винтовые пары. Для упрощения системы полезно рассматривать все, что находится за пределами вала двигателя, как черный ящик с некоторой отраженной инерцией вращательной нагрузки (IL). Для расчета инерции системы, отражаемой на валу двигателя, требуется хорошее понимание системы; это можно сделать с помощью онлайн-инструментов производителя двигателя, программного обеспечения САПР или стандартной формулы, доступной для стандартной геометрии.

Требования к крутящему моменту и мощности в центре внимания

На рис. 2 показаны рабочие кривые для типичного двигателя. Для непрерывной работы не следует превышать максимальное значение постоянного крутящего момента, так как это максимальное значение крутящего момента, при котором не произойдет перегрева. Однако для прерывистого использования возможны более высокие крутящие моменты. По мере увеличения угловой скорости способность двигателя развивать крутящий момент уменьшается. Таким образом, если требуются более высокие скорости и крутящий момент, чем может обеспечить конкретный двигатель, необходимо выбрать более мощный двигатель.

Рис. 2: Кривые работы двигателя

Рис. 3: Двигатель, приводящий в действие барабанный подъемник

Возьмем в качестве примера двигатель, который используется для привода барабанного подъемника и подъема груза, как показано на рис. 3. Максимальный крутящий момент, который мы должны учесть, — это крутящий момент, необходимый для подъема груза при постоянной скорость плюс крутящий момент, необходимый для разгона до этой скорости из состояния покоя. Крутящий момент (T + I _M ) требуется от двигателя, который нужен по нагрузке (T + I _L или T + I _L /n для редукторной нагрузки) и для разгона двигателя (I + I _M x α + I _M ) можно записать как: T + I _M = T + I _L /n + I + I _M x α + I _M (уравнение 4). Угловое ускорение груза α + I _L определяется выражением α + I _M = n x α + I _L (уравнение 5), и с учетом дополнительного крутящего момента (T + I _f ), необходимый для преодоления трения нагрузки, крутящий момент, используемый для ускорения нагрузки, будет T + I _L = I + I _L x α + I _L + T + I _f (уравнение 6 ).

•	Если мы подставим T + I L и α + I M из уравнений 5 и 6 в уравнение 4, мы можем записать общее выражение для крутящего момента двигателя для редукторных приводов как T + I M = 1/ n [ T + I f + αL x (I + I L + n 2 x I + I M )]
•	Учитывая дополнительный крутящий момент (T + I f ), необходимый для преодоления трения нагрузки из уравнения 3, мы можем записать общее выражение для крутящего момента двигателя для прямых приводов как T + I M = T + I f + α х (I L + I M ),

Двигатель должен иметь возможность работать на максимальной требуемой скорости без перегрева. Полная необходимая мощность (P) представляет собой сумму мощности, необходимой для преодоления трения, и мощности, необходимой для ускорения груза. Поскольку мощность является произведением крутящего момента и угловой скорости, то мощность, необходимая для преодоления момента трения (T + I _f ) равно T + I _f x ω, при этом мощность, необходимая для разгона груза с угловым ускорением (α) равна (I + I _L α) ω, где I + I _L – момент инерции груза. Таким образом, общее выражение для мощности двигателя имеет вид P = T + I _f x ω + I + I _L x α x ω.

Подводя итог вышеизложенному, можно сказать, что при выборе любого двигателя ключевыми факторами, которые следует учитывать, являются требования к крутящему моменту и мощности. Для требовательных приложений, требующих либо высокого ускорения и замедления, либо чрезвычайно точного позиционирования для достижения желаемой производительности, согласование инерции также становится важным. Свяжитесь с нами здесь для получения более подробной информации!

машиностроение — Расчет требуемого крутящего момента двигателя

Задавать вопрос

спросил 1 год, 2 месяца назад

Изменено 1 месяц назад

Просмотрено 494 раза

$\begingroup$

Я хочу знать, какой крутящий момент мне нужен для моего двигателя.

Представьте себе колесо с двигателем в центре. Вот такой:

Допустим, колесо имеет размеры 400 мм, весит 10 кг, по какой формуле можно сделать такой расчет?

Я думаю, что формула (поправьте меня, если я ошибаюсь): 𝑇=𝐹⋅𝑎

 Диаметр: 400 мм = 40 см = 0,4 м
Сила: 10 кг = 100 Н
𝑇=𝐹⋅𝑎
𝑇=100⋅0,4
𝑇=40 Нм
 

То есть мне для работы нужен двигатель с крутящим моментом не менее 40 Нм (в теории, на практике было бы около 50 Нм, что уж говорить), да?

Источник: https://x-engineer.org/power-vs-torque/

Я спрашиваю, потому что я не эксперт, вы видите ошибки?

• машиностроение
• механизмы

$\endgroup$

1

$\begingroup$

См. здесь фактический расчет: Как рассчитать мощность и крутящий момент, необходимые для двигателя колесного робота/транспортного средства?

Но это не относится к принципам, и из вашего вопроса я думаю, что это потребуется, чтобы прояснить, как все работает:

1. $F=ma$ является линейным, но имеет вращательный эквивалент $\tau=I \alpha$, где $I$ – момент инерции, $\tau$ – крутящий момент, а $\alpha$ – угловое ускорение (радиан в секунду). Масса и вес не смешиваются с крутящим моментом.
2. Момент инерции является вращательным эквивалентом массы и получается из геометрии массы и . Для колеса это будет цилиндр или круг. Вы бы искали уравнение для вашей формы в таблице уравнений момента инерции, чтобы выяснить, что вам нужно для простых форм
3. Сила, приложенная к краю колеса, и радиус/длина плеча рычага определяют крутящий момент. Сила, приложенная к краю колеса, не является весом. Вы можете преобразовать крутящий момент в силу, если у вас есть радиус/длина рычага: $\tau=Fr$
4. Я предполагаю, что вас интересует не раскручивание колеса в свободном пространстве, а перемещение автомобиля. Таким образом, вы не будете использовать массу колеса или момент инерции колеса. Вы бы применили усилие на краю колеса, необходимое для ускорения масса автомобиля до скорости плюс сила, необходимая для преодоления трения качения, наклона против силы тяжести, сопротивления воздуха, которые необходимы для поддержания скорости после того, как автомобиль разогнался.
5. Использование уравнения из № 1 позволяет рассчитать только крутящий момент, необходимый для раскручивания колеса, как если бы это был маховик в космосе, над землей.
6. Что касается раскручивания колеса при дальнем движении, вам нужно будет учитывать этот эффект только в том случае, если для ускорения автомобиля требуется значительная часть крутящего момента, а это не так, поэтому вы можете пренебречь этим.
7. Без потерь, таких как трение или гравитация, притягивающая вниз на склоне, ускорение автомобиля до скорости похоже на раскручивание маховика в том смысле, что вы прикладываете силу только для того, чтобы разогнать его до скорости. После этого он продолжает двигаться с той же скоростью, если убрать ускоряющую силу согласно Исааку Ньютону. В реальной жизни есть потери, такие как трение, поэтому вам нужно приложить дополнительную силу / крутящий момент, чтобы преодолеть эти потери. Но как только они преодолены, создается впечатление, что трение и гравитация исчезают, так как они нейтрализуются, поэтому любая дополнительная сила сверх этого превращается в ускорение, как если бы оно было без трения или летело в космосе. Как только автомобиль или маховик набирают скорость, вы можете удалить эту дополнительную силу/крутящий момент для ускорения, и пока вы сохраняете силу/крутящий момент для преодоления потерь, таких как трение, скорость сохраняется. Вот почему движение по автостраде легче для двигателя, чем начало и остановка движения.
8. Обратите внимание, что помимо преодоления потерь для поддержания скорости (будь то скорость равна нулю или не равна нулю), ускорение влияет на все остальное, поэтому вам нужно указать, какое ускорение вы хотите.
9. Если бы двигатель прикладывал усилия, достаточные для поддержания скорости, а ваша скорость была бы нулевой, это было бы похоже на то, как если бы ваша машина неподвижно стояла на ледяной поверхности без трения. Если вы толкаете его в правильном направлении, вся эта сила является дополнительной, поэтому он разгоняется до скорости, основанной на силе толкания, а затем продолжает двигаться с этой скоростью, поскольку двигатель преодолевает трение.

$\endgroup$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.