Расчет мощности электродвигателя — ElectrikTop.ru
Если вы задались целью создать электрический привод, например, собственную мельницу, насосную станцию, транспортерную ленту или другое полезное в хозяйстве устройство, вам надо найти или купить электродвигатель и убедиться в том, что его мощность соответствует поставленным задачам.
Сегодня мы осветим некоторые аспекты, касающиеся устройства и рабочих качеств электрических машин, что поможет вам сделать правильный выбор.
Как выбрать электродвигатель
Подбор электродвигателя стоит начать со знакомства с типами электрических машин. Основное их отличие состоит в способе взаимодействия магнитных полей статора и ротора. По этому признаку они делятся на два типа:
- Синхронные.
- Асинхронные.
Синхронные электрические машины
У них магнитное поле статора и ротора создается внешними источниками, они независимы друг от друга, их смена положения их полюсов происходит синхронно.
Двигатели постоянного тока
Исходя из принципа механики Ньютона, утверждающего, что всякое движение относительно, электродвигатель постоянного тока можно назвать синхронной машиной. Хотя магнитные поля статора и ротора в ней неподвижные, а вращение вала происходит за счет эффекта отталкивания одноименных полюсов магнитов и притягивания разноименных.
Синхронизация их положения относительно друг друга происходит особого устройства – коллектора, расположенного на валу ротора. Это кольцо из меди, поделенное на секторы диэлектриком. Концы обмоток ротора подключаются к этим секторам и создают контактные пары.
На них через угольные щетки подается постоянный ток. Во время вращения вала происходит переключение полюсов между парами. Магнитное поле статора может создаваться металлами с остаточным магнетизмом или прохождением тока по обмоткам. Последние применяются в электрических машинах большой мощности.
Их достоинством является большой коэффициент полезного действия, до 98%, а также стабильно высокий вращающий момент и малая зависимость от перегрузок.
Ими очень просто управлять: для снижения скорости вращения надо лишь уменьшить величину подаваемого напряжения, а для реверсирования достаточно сменить полярность. Недостатком является сложность устройства и невысокая надежность щеточного узла, его склонность к искрению и шумность. Кроме того, постоянное напряжение сложно передавать на большие расстояния, из-за чего нет магистральных линий такого типа. Питание придется создавать самостоятельно, используя выпрямительные или инверторные схемы. Также про двигатели постоянного тока можно почитать здесь.
Коллекторные двигатели
По своей конструкции они аналогичны двигателям постоянного тока. Однако питаются переменным однофазным током. Статорная обмотка возбуждения у них включена последовательно с обмоткой якоря. Вращение вала происходит за счет синхронной смены полюсов магнитного поля в статорной и роторной обмотках.
К перечисленным выше достоинствам – большому вращающему моменту, нечувствительности к перегрузкам, стоит отнести и то, что это единственная электрическая машина переменного тока, которой можно без проблем управлять.
Для изменения скорости вращения вала достаточно уменьшить питающее напряжение, а для реверсирования поменять местами точки подключения коллекторного узла со статорной обмоткой. Поэтому коллекторные электродвигатели широко применяются в бытовых электроприборах.
Например, в стиральных машинах, дрелях и другом электрифицированном инструменте. К недостаткам, основным из которых является сложность и малая надежность щеточного узла, стоит отнести и невозможность подключения трехфазного напряжения. Просто потому, что в этом случае щеток должно быть шесть. Это ограничивает максимальную мощность двигателей: у однофазных машин при напряжении 220 вольт это значение не бывает более 2,5 киловатта.
Синхронные электродвигатели переменного тока
У них статорная обмотка питается переменным трехфазным током, а роторная – постоянным. Чтобы их магнитные полюса сцепились и вызвали движение вала, такой электродвигатель надо раскрутить вручную или другим мотором. Фактически они являются генератором переменного тока, работающим в режиме вращения. Достоинством машины являются высокий крутящий момент и стабильность частоты вращения.
Недостатками – сложность пуска и наличие коллектора со щеточным узлом, что снижает их надежность. А также невозможность регулирования частоты вращения. Применяются в установках, которые работают постоянно или с очень длительным рабочим циклом. Например, на перекачивающих станциях или транспортерных лентах.
Узнать больше об электродвигателях можно узнать в нашей статье «Электрический двигатель: виды и характеристики».
Асинхронные электрические машины
В них магнитное поле ротора является порождением вращающегося магнитного поля статора. Поскольку между этими деталями машины есть воздушный зазор, передача энергии между ними происходит с потерями. Поэтому фаза тока в роторе отстает от фазы тока в статоре на небольшой угол (не более 100), который определяет величину коэффициента мощности cosφ. Это отставание и является причиной того, что электрическую машину этого типа называют асинхронной.
Поскольку между этими деталями машины есть воздушный зазор, передача энергии между ними происходит с потерями. Поэтому фаза тока в роторе отстает от фазы тока в статоре на небольшой угол (не более 100), который определяет величину коэффициента мощности cosφ. Это отставание и является причиной того, что электрическую машину этого типа называют асинхронной.
Двигатели с короткозамкнутым ротором
Обмотка ротора у них – это набор металлических стержней, которые соединяют два кольца. Получившуюся фигуру называют «беличье колесо». В момент подачи напряжения на статорную обмотку в роторе возникает ток короткого замыкания, энергия которого тратится на раскручивании вала и тем самым гасится. У него несколько меньший КПД, чем у синхронных машин, он не превышает 80%.
После набора оборотов он имеет очень стабильный вращающий момент на валу и хорошо выдерживает перегрузки. Главными достоинствами таких двигателей является его простота и надежность, благодаря которым они очень широко распространены. Недостатками – сложность управления.
Недостатками – сложность управления.
Для изменения скорости вращения необходимо менять частоту питающего напряжения или количество статорных обмоток, которое определяет количество полюсов электромагнита – чем их больше, тем она ниже. Также электродвигателям с короткозамкнутым ротором свойственен большой пусковой ток, перегружающий сеть, а также резкий рост вращающего момента при подключении питания, что может вызвать поломку редуктора привода.
Двигатели с фазным ротором
Пуск асинхронных двигателей с короткозамкнутым ротором большой мощности (более 30 кВт) связан с чрезвычайной перегрузкой питающей сети. Для устранения этого явления используют машины с фазным ротором, обмотка которых состоит из трех катушек, соединенных звездой. Их концы соединены угольными щетками с тремя контактными кольцами, расположенными на оси двигателя.
В отличие от коллектора двигателя постоянного тока они не поделены на сектора. При запуске такой машины используется трехфазный реостат, сопротивление которого в момент пуска максимальное. Постепенно уменьшая активное сопротивление ротора, добиваются плавной раскрутки вала электродвигателя. При достижении номинальных оборотов его закорачивают.
Постепенно уменьшая активное сопротивление ротора, добиваются плавной раскрутки вала электродвигателя. При достижении номинальных оборотов его закорачивают.
Изменяя сопротивление ротора, можно добиться изменения частоты вращения. Достоинством машины такого типа является отсутствие перегрузки в момент запуска и плавное нарастание вращающего момента. Поэтому ее применяют в грузоподъемном оборудовании. Недостаток – сложность устройства и более низкий, чем у машин с короткозамкнутым ротором КПД, он не более 60%.
Читайте также «Как работает асинхронный электродвигатель».
Как рассчитать мощность электродвигателя
При расчете мощности электродвигателя надо ориентироваться на потребности обеспечиваемого технологического процесса. В Сети так много методичек для определения этого параметра, что вы можете запутаться окончательно. Предлагаем вам довольно простую универсальную формулу, пригодную для любых случаев.
P = T ∙ Ω
P – мощность электродвигателя. Т – потребный вращающий момент на валу, а Ω – угловая скорость.
T = Ft ∙ R
Ft– потребное тяговое усилие, оно рассчитывается по формуле: Ft= t ∙ M ∙ 2.5, где t – коэффициент трения (для подшипников качения он равен 0.02), М – масса перемещаемого груза, а 2.5 – это коэффициент Ньютона. R – радиус рабочего органа, например, крыльчатки насоса.
Ω = π ∙ n / 30, где π = 3.14, а n – паспортная частота вращения приводимого в действие устройства.
Полученное значение лучше увеличить в 1,5 раза, чтобы предусмотреть возможные перегрузки во время работы привода.
При расчете рабочего тока электродвигателя необходимо учитывать, что при соединении обмоток статора асинхронного электродвигателя звездой он в 1,73 раза меньше, чем при соединении треугольником. На эту же величину уменьшается и мощность.
Окончательно убедиться в работоспособности созданного привода вы сможете только на практике.
Мощность и коэффициент полезного действия — урок. Физика, 8 класс.
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы \(A\) и обратно пропорциональна времени \(t\), за которое работа была совершена.
Мощность \(N\) определяют по формуле:
N=At.
Единицей измерения мощности в системе \(СИ\) является \(Ватт\) (русское обозначение — \(Вт\), международное — \(W\)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л. с.), 1 л.с. = 736 Вт.
с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно \(90 л.с. = 66240 Вт\).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля \(F\) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать \(100\) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах \(40 — 45\) %. Таким образом, получается, что только около \(40\) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах \(40 — 45\) %. Таким образом, получается, что только около \(40\) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля \(20\) литров бензина, тогда только \(8\) литров будут расходоваться на перемещение автомобиля, а \(12\) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита \(«эта»\) η, он является отношением полезной мощности \(N\) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы \(A\) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше \(1\), или \(100\) % (η < 1, или η < \(100\) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
формула, мгновенный и средний расчет силы
В общем смысле этим термином обозначают энергетические изменения определенной системы. Классическая формула механической мощности устанавливает связь между работой и временем, которое понадобилось на завершение соответствующего процесса. В этой публикации дополнительно рассмотрены электрические и гидравлические параметры энергии, методики вычислений, измерительные приборы.
В этой публикации дополнительно рассмотрены электрические и гидравлические параметры энергии, методики вычислений, измерительные приборы.
Механическая мощность характеризует скорость выполнения работы
Используемые обозначения
В стандартных формулах мощность часто обозначают буквой N без уточнения происхождения. Достаточно часто применяют P. В этом варианте понятен исходный смысл: от латинского слова potestas – действие, мощь, сила. В электротехнике часто применяют W (watt – англ., ватт). Дополнительными символами отмечают специфическое назначение NH – гидравлическая мощность от hydraulics.
Основные формулы
Когда рассчитывается средняя мощность формула содержит значения для определенных промежутков: ΔА (работа) и Δt (время). Мгновенные показатели обозначают dA и dt, соответственно. Чтобы узнать количество потребленной энергии, берут интеграл за необходимый временной интервал.
Единицы измерения
В действующей системе единиц «СИ», утвержденной на международном уровне, мощность предлагается указывать в ваттах (один Вт = работе 1 Джоуль, сделанной за 1 секунду).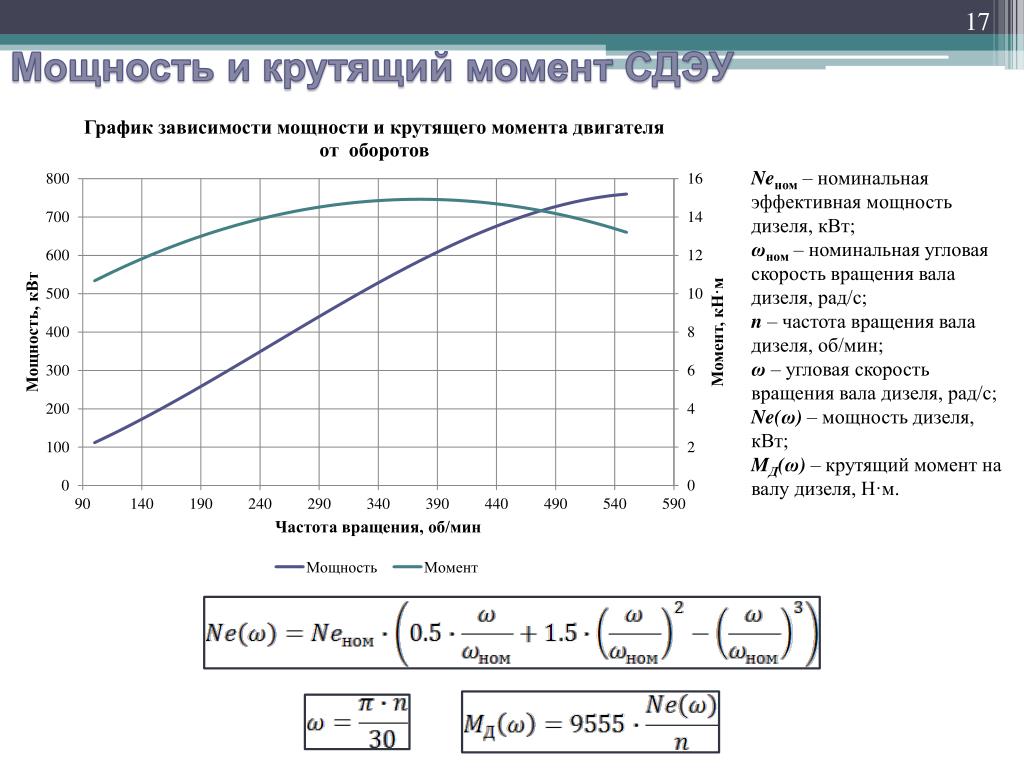 Устаревшее обозначение «лошадиная сила» рекомендовано изъять из оборота. Для удобства применяют производные значения с определенными приставками (один киловатт (1кВт) = 10 в третьей степени ватт = 1 000 Вт).
Устаревшее обозначение «лошадиная сила» рекомендовано изъять из оборота. Для удобства применяют производные значения с определенными приставками (один киловатт (1кВт) = 10 в третьей степени ватт = 1 000 Вт).
Перевод 1 Вт в иные обозначения:
- килограмм-сила-метр в секунду (кгс*м/с) – 0,102;
- эрг в секунду (эрг/с) – 107;
- лошадиная сила (л.с.) метрическая/ английская – 1,36*10-3/ 1,34*10-3.
К сведению. Если в описании автомобиля указано 125 кВт, это равнозначно 170 л.с. (125*1,36=169,95).
Мощность в механике
В ходе исследования механических процессов необходимо учитывать точку приложения усилия и направление действия. Рассчитать мощность можно по формуле (N=F*v) с учетом скорости движения (v) определенного тела. Если направления не совпадают, добавляют корректирующий множитель (cosα).
Электрическая мощность
В этой области не важны тяжесть предметов, сила трения, другие механические термины и определения. Тем не менее, суть рассматриваемой физической величины остается неизменной, подобны принципы отдельных вычислений.
Тем не менее, суть рассматриваемой физической величины остается неизменной, подобны принципы отдельных вычислений.
Можно применить для расчета мгновенной мощности формулу:
P(a-b) = А/ Δt,
где:
- (a-b) – обозначают энергию, затраченную на перемещение заряда (q) из одной в другую точку;
- А – выполненная в ходе этого процесса работа.
Если взять все заряды (Q), напряжение в контрольных точках (U), нетрудно вычислить суммарную мощность:
P = (U/ Δt) * Q = U * Q/ Δt = U *I.
Последнее преобразование основано на классическом определении тока (количество зарядов, протекающих по соответствующему проводнику за определенное время).
Для пассивных цепей можно пользоваться законом Ома и соответствующими формулами без дополнительных коррекций. Учитывают (при наличии) источник электродвижущей силы (направление движения токов).
Формулы для расчета мощности и других параметров
При подключении техники к источникам переменного тока вычисления усложняются. Приходится интегрировать мгновенные значения с учетом определенных периодов, частоты и формы сигналов. На практике часто решают задачи по вычислению мощности потребителей, подключенных к источнику питания с синусоидальным током (напряжением).
Активная составляющая энергии в этом случае будет зависеть от фазового сдвига. Значение вычисляют по формуле:
Pa = U * I * cosϕ (для 220V).
При работе с трехфазными источниками пользуются измененным вариантом выражения:
Pa = √3 * U * I * cosϕ = 1,732 * U * I * cosϕ.
Реактивная переменная потребляется и возвращается в источник питания. Для расчета берут следующую зависимость базовых параметров:
Pq = U * I * sinϕ.
Полная мощность:
Ps = √( Pa2 + Pq2).
Приборы для измерения электрической мощности
С учетом основных компонентов формулы несложно понять, что значения необходимых параметров (ток и напряжение) можно узнать с помощью обычного мультиметра. По необходимому уровню точности выбирают методику и класс измерительного прибора.
По необходимому уровню точности выбирают методику и класс измерительного прибора.
Современный ваттметр может передавать информацию в режиме онлайн для удаленного контроля телеметрии
Специализированные изделия (ваттметры) способны отображать результаты исследований при работе в сетях постоянного и переменного тока. Специальные модификации (варметры) замеряют реактивную составляющую.
Гидравлическая мощность
Узнать производительность асинхронного электродвигателя насоса можно косвенным методом, по выполненной работе. Для этого умножают перепад измеренных (вход/ выход) давлений (ΔP) на количество перекачанной жидкости (V) в м куб. за секунду.
Пример:
- напор по манометрам – 220 кгс/ см кв.;
- производительность – 65 л/мин. = 3,9 куб. м/ час = 0,001083 куб. м /с.;
- мощность NH = ΔP * V = 220 * 100 (перевод см в м) * 0,001083 = 23,83 кВт.
Мощность силы
Для решения практических задач меняют рассмотренные выражения необходимым образом. Расчет энергетических изменений отображает пример с падающим предметом:
Расчет энергетических изменений отображает пример с падающим предметом:
- в исходных данных известны высота и масса тела;
- требуется установить мощность силы формула которой отображает результат на половине пути при свободном падении;
- подставляют вместо базовых компонентов известные величины:
- F = m *g;
- V (скорость в определенной точке) = Vn (начальная скорость) + g*t.
- после завершения преобразований получают:
P = m*√(g3*h).
Мощность вращающихся объектов
Для расчета подобной системы применяют формулу:
N = M * w = (2π * M* n)/60,
где:
- M – момент силы;
- w – угловая скорость, характеризующая вращение;
- n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.
Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.
Видео
Расчетные формулы основных параметров асинхронных двигателей
В таблице 1 представлены расчетные формулы для определения основных параметров асинхронных двигателей.
В данной таблице собраны все формулы, которые касаются расчета параметров асинхронных двигателей.
Используя формулы из данной таблицы, вам больше не придется искать нужную формулу в различных справочниках.
Таблица 1 — Расчетные формулы для определения основных параметров асинхронных двигателей
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Потребляемая активная мощность из сети, кВт | U1, I1 – линейные значения напряжения, В и тока двигателя, А; cosϕ – коэффициент мощности; | |
| Потребляемая реактивная мощность, квар | ||
| Полезная мощность на валу, кВт | Ƞ — КПД двигателя; | |
| Потребляемый двигателем ток, А | ||
| Вращающий момент двигателя, кГм | nном. – номинальная скорость вращения ротора, об/мин; – номинальная скорость вращения ротора, об/мин; | |
| Синхронная скорость вращения магнитного поля, об/мин | f1 – частота питающего тока, Гц; р – число пар полюсов машины; | |
| Скольжение двигателя | ||
| Скорость вращения ротора при нагрузке, об/мин | ||
| ЭДС обмоток статора и ротора, В | kоб.1, kоб.2 – обмоточные коэффициенты статора и ротора, равные произведению коэффициентов укорочения kу шага и распределения обмотки kw; kоб. = kу* kw; | |
| Коэффициенты трансформации по напряжению и по току | w1, w2 – числа витков обмоток статора и ротора; m1, m2 – числа фаз в обмотках статора и ротора.  У двигателей с фазным ротором. У двигателей с фазным ротором.m2 = 3 у двигателей с короткозамкнутым ротором; m2 = z2, т.е. числу пазов в роторе. | |
| Параметры схемы замещения | zк, rк, хк – полное, активное и индуктивное сопротивления при КЗ двигателя, Ом; Iп – пусковой ток двигателя, А; ∆Рк – суммарные потери в меди статора и ротора двигателя, Вт; r1, x1 – активное и индуктивное сопротивления обмотки статора, Ом; r2’, x2’ – активные и индуктивные сопротивления ротора, приведенные к обмотке статора, Ом; | |
| Ток холостого хода, А | Iном. – номинальный ток двигателя, А | |
| Критическое скольжение | sinϕ – коэффициент реактивной мощности; kм – коэффициент перегрузочной способности; | |
| Уравнение вращающего момента | Sном. – скольжение при номинальной нагрузке – скольжение при номинальной нагрузке | |
| Скольжение двигателя s2 при введении добавочного сопротивления в ротор | ||
| КПД двигателя при введении добавочного сопротивления в ротор | ||
| Критический максимальный момент, развиваемый в двигательном (+) и генераторном (-) режимах, кГм | U1ф – фазное напряжение, В | |
| Уравнение вращающего момента при добавочном сопротивлении в цепи ротора |
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
активное сопротивление двигателя, полное сопротивление двигателя, реактивное сопротивление двигателя, ток двигателяПоделиться в социальных сетях
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Мощность момент — Энциклопедия журнала «За рулем»
Может ли бульдозер обогнать «формулу 1»? Может, но только на очень короткой дистанции
Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал. Крутящий момент может существовать и сам по себе, без мощности. Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F. Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.
Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того! Ракетчики, например, запрягают пламя напрямую, получают гигантские тяги и мощности, но о крутящих моментах вспоминают лишь в расчетах турбонасосных агрегатов, – да и то, если двигатели не твердотопливные!
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил.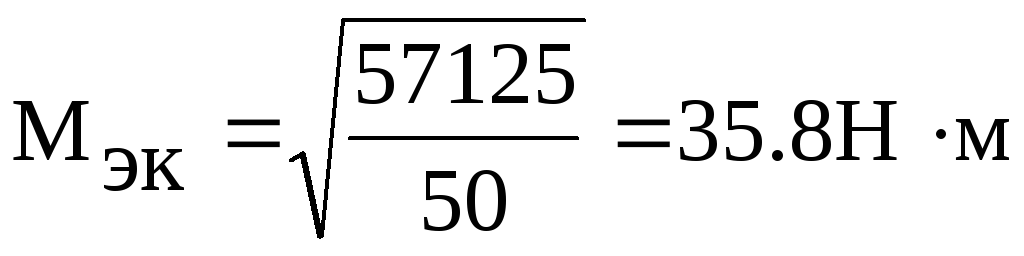 Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Итак, имеем дело с формулой (1). К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт.
3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт.
На всякий случай напомним, что 1 лс = 75 кгм/сек = 75 • 9,81 Нм/сек = 735,75 Вт. Поэтому 107846 Вт ≈ 146,6 л.с.
А теперь прикинем мощность «формульного» двигателя с таким же скромным моментом, но при оборотах 18 тысяч! Результат – 880 л.с. (647 кВт), которые обеспечивают машине роскошную динамику. Никакого чуда нет: чем больше циклов совершит наш «моментик» за одну секунду, тем больше и совершенная им работа. Еще пример. В авиатехнике ныне практически господствуют газотрубинные двигатели. Повторив наш расчет для небольшого двигателя, с оборотами свободной турбины 40 тысяч в минуту, получим мощность около 1950 л.с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает!
Но вернемся к автомобилю. Как уже сказано, любому комфортней ездить на машине, у которой под капотом достаточно и мощности, и момента. Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость!
Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость!
Гусеничному трактору дернуться и оборвать сцепку – плевое дело. Это похоже на выстрел из ружья – можно на миг и «формулу I» опередить. А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек2. А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
Низшая передача бульдозера крайне «коротка»: чуть «перекрутил» – тяга упала. А другие не лучше, – вон и «формула» уже растворилась за горизонтом, так что для серьезных игрищ «мощи» на гусеницах маловато.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.
Рис. 1. Величины мощности N1 … N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Вся история современной транспортной техники – это непрерывная борьба за большие мощности. У наиболее знаменитых ракетоносителей они давно превысили 100 миллионов кВт. Это не ошибка — именно 100 000 000 000 Вт, или 100 ГигаВатт. И
Эффективная мощность двигателя
Полезная мощность, передаваемая двигателем потребителю, именуемая эффективной мощностью Nе, меньше, чем Ni, на величину механических потерь.
Эти потери обусловлены трением поршня и подшипников, затратой работы на насосы — топливный, продувочный, водяной и пр. Известно, что механические потери учитываются механическим к. п. д., т. е.
?м = Nе / Ni ,
и поэтому
Ne = ?мNi.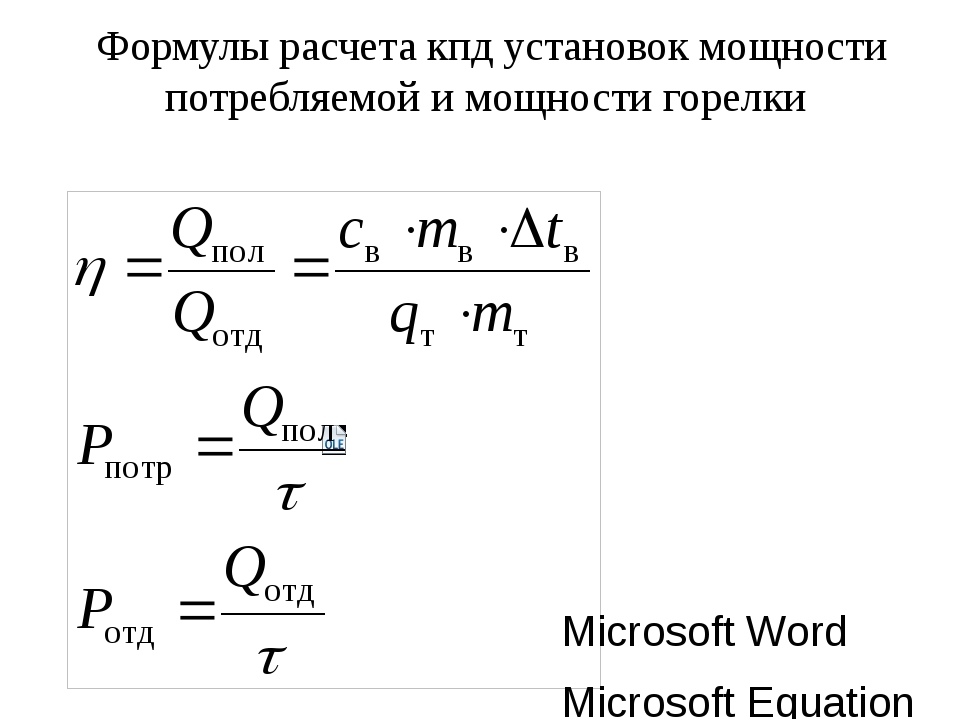 (11,28)
(11,28)
Средние значения механического к. п. д. у различных двигателей колеблются в пределах 0,7—0,9.
Если мощность, соответствующую механическим потерям, обозначить через Nr, то
Ne= Ni – Nr .
Разделим все части этой формулы на коэффициент К. Для четырехтактного двигателя К =Vhni /900, для двухтактного К = Vhni /450.
Тогда
Ne / K = Ni /K – Nr / K .
Из формул (II, 24) и (II, 25) видно, что член Ni /K представляет
собой среднее индикаторное давление pi. По аналогии с этим член
По аналогии с этим член
Ne / K называют средним эффективным давлением ре.
Физический смысл его таков: это та часть среднего индикаторного давления, которая пропорциональна работе, отдаваемой двигателем потребителю.
Член Nr / K = рr соответствует той части среднего индикаторного
давления, которая пропорциональна работе, затраченной на механические потери.
Величины ре и рr имеют большое значение при расчете и сравнении показателей различных типов двигателей.
Из формул (II, 24), (II, 25), (II, 28) и (II, 30) следует: для четырехтактных двигателей
В современных четырехтактных дизелях без наддува в среднем 5 < pе < 8 кГ/см2. В двухтактных дизелях, где часть хода поршня отводится на процесс выпуска, ре соответственно оказывается ниже примерно на 20%. Наиболее низкие ре, порядка 2,5 кГ/см2, встречаются у двигателей с картерной продувкой
При наддуве ре может быть значительно поднято — до 15 кГ/см2 и выше.
Расчет мощности двигателя
Следующие два калькулятора можно использовать для оценки мощности двигателя транспортного средства на основе веса транспортного средства, затраченного времени и скорости, использованной для завершения пробега на четверть мили.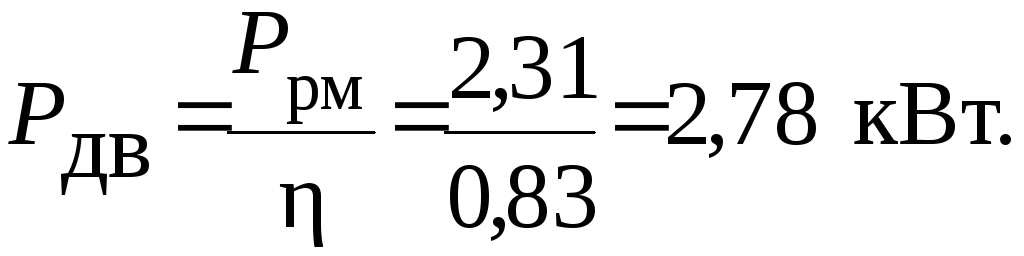 Вес транспортного средства должен включать не только транспортное средство, но также водителя, пассажира и все, что имеет значительный вес. Чтобы оценить максимальную мощность в лошадиных силах, от начала до конца следует применять максимальную производительность. Результаты всех расчетов являются приблизительными.
Вес транспортного средства должен включать не только транспортное средство, но также водителя, пассажира и все, что имеет значительный вес. Чтобы оценить максимальную мощность в лошадиных силах, от начала до конца следует применять максимальную производительность. Результаты всех расчетов являются приблизительными.
Метод истекшего времени (ET)
Этот метод использует вес транспортного средства и прошедшее время (ET) для прохождения четверти мили (402,3 метра) по формуле
| Лошадиная сила = | Вес |
| (ET / 5.825) 3 |
Метод скорости ловушки
В этом методе используются вес транспортного средства и скорость, с которой транспортное средство проехало четверть мили (402,3 метра) по формуле
| Лошадиная сила = Вес × ( | Скорость | ) 3 |
| 234 |
 Используемая скорость должна быть скоростью, достигнутой на четверть мили, а не средней скоростью.
Используемая скорость должна быть скоростью, достигнутой на четверть мили, а не средней скоростью. Меры предосторожности
При измерении прошедшего времени или скорости улавливания при максимальной мощности двигателя необходимо соблюдать особые меры предосторожности. Во-первых, все водители должны точно знать, что они делают. Неопытность может привести к последствиям, некоторые из которых могут быть серьезными и опасными для жизни. Во-вторых, не измеряйте прошедшее время на четверти мили на общественных улицах или шоссе; превышение скоростного режима запрещено законом, и внимание следует уделять вождению, а не измерению времени.Эти действия могут представлять опасность не только для водителя, но и для других людей. Существуют законные места для измерения прошедшего времени, например, на драг-полосах, сельских дорогах, находящихся в частной собственности, а также во время специальных мероприятий, которые проходят на гоночных трассах или в аэропортах. В-третьих, убедитесь, что транспортное средство находится в полном рабочем состоянии, так как доведение транспортного средства до предела влечет за собой определенный риск. Убедитесь, что шины накачаны и надежно закреплены, подушки безопасности исправны, двигатель правильно настроен и находится в хорошем состоянии.
Убедитесь, что шины накачаны и надежно закреплены, подушки безопасности исправны, двигатель правильно настроен и находится в хорошем состоянии.
Что такое мощность?
Идея лошадиных сил была придумана инженером Джеймсом Ваттом, инженером 19 -х годов века, который построил некоторые из первых паровых двигателей. Работа Ватта была замечательной, и в честь него его именем была названа единица мощности, ватт (нет, он не изобрел лампочку, но его имя написано на каждой).
Ватт работал в шахте, используя лошадей, чтобы тянуть фургоны с углем. Он хотел определить, сколько угля пони может втащить в повозку на заданную длину.Он измерил, сколько футов лошадь может вытащить 22 000 фунтов угля за одну минуту. Затем он увеличил это количество до 33 000 футов-фунтов в минуту и назвал это лошадиными силами.
Это совершенно произвольная величина, но она стала мерой того, сколько работы могут выполнять двигатели — никто никогда раньше этого не измерял. Итак, представьте лошадь, вытаскивающую фургон с углем из шахты; с усилием в 1 л. с. лошадь тянет 330 фунтов угля на 100 футов за одну минуту.
с. лошадь тянет 330 фунтов угля на 100 футов за одну минуту.
Измерение мощности в лошадиных силах
Мощность в лошадиных силах измеряется динамометром, который представляет собой ротор в корпусе.Чтобы заставить ротор вращаться с определенной скоростью, требуется определенная мощность.
Если вы поставите автомобиль на нейтраль, а затем опустите двигатель, когда он прикреплен к динамометру, устройство нагружает двигатель и определяет, может ли он повернуть нагрузку или как быстро он может повернуть нагрузку. Если вы запустите двигатель со скоростью 5000 оборотов в минуту (об / мин), вы увидите, какая нагрузка включается на динамометр для расчета мощности.
Каждый двигатель имеет пиковую мощность — значение оборотов, при котором мощность, доступная от двигателя, является максимальной.Вы часто увидите, что это выражается в брошюре или обзоре журнала как «320 л.с. при 6500 об / мин».
Полная или полезная мощность в лошадиных силах
Полная мощность в лошадиных силах — это мера выходной мощности двигателя на динамометре, когда двигатель не подключен к обычным аксессуарам, используемым в движущемся автомобиле. Полезная мощность в лошадиных силах измеряет выходную мощность двигателя при подключении к аксессуарам с ременным приводом, таким как водяные насосы, насосы гидроусилителя рулевого управления и генераторы переменного тока. Существуют также паразитные потери мощности, вызванные лобовым сопротивлением трансмиссии и проскальзыванием муфты или гидротрансформатора, которые учитываются в чистой мощности.В результате приведения в действие этих движущихся частей полезная мощность может быть значительно ниже, чем полная мощность.
Полезная мощность в лошадиных силах измеряет выходную мощность двигателя при подключении к аксессуарам с ременным приводом, таким как водяные насосы, насосы гидроусилителя рулевого управления и генераторы переменного тока. Существуют также паразитные потери мощности, вызванные лобовым сопротивлением трансмиссии и проскальзыванием муфты или гидротрансформатора, которые учитываются в чистой мощности.В результате приведения в действие этих движущихся частей полезная мощность может быть значительно ниже, чем полная мощность.
Мощность в сравнении с крутящим моментом
Крутящий момент определяется как вращающая сила. Он измеряется как величина силы, умноженная на длину рычага, через который она действует. Например, если вы используете гаечный ключ длиной один фут для приложения силы 10 фунтов к головке болта, вы создаете крутящий момент 10 фунт-фут. Обратите внимание, что крутящий момент измеряется в фунт-футах, а мощность — в фут-фунтах в секунду.
Крутящий момент — это сила, которая может толкать автомобиль вперед. При заданной массе автомобиля высокий крутящий момент означает, что автомобиль может ускоряться быстрее и более отзывчив. Хотя это не всегда верно, как правило, чем больше крутящий момент вырабатывает двигатель, тем больше у него рабочего потенциала. Точно так же двигатель, который производит больше лошадиных сил, обычно имеет большую способность генерировать более высокий крутящий момент.
При заданной массе автомобиля высокий крутящий момент означает, что автомобиль может ускоряться быстрее и более отзывчив. Хотя это не всегда верно, как правило, чем больше крутящий момент вырабатывает двигатель, тем больше у него рабочего потенциала. Точно так же двигатель, который производит больше лошадиных сил, обычно имеет большую способность генерировать более высокий крутящий момент.
Чтобы лучше понять взаимосвязь между мощностью и крутящим моментом, подумайте о разнице между гоночным автомобилем и трактором.Гоночный автомобиль легкий, поэтому его высокий уровень мощности передает крутящий момент через систему передач, заставляя его двигаться быстро. С другой стороны, трактор — это массивная тяжелая машина, предназначенная для работы. Трактор не может двигаться быстро, но его передача передает крутящий момент, так что он может толкать и тянуть. Если поставить один и тот же мощный двигатель на гоночный автомобиль и трактор, в результате получится быстрая гоночная машина, но не машина, способная разрушить бетонную стену. Медленный трактор прикладывает свою работу к давлению на стену и разрушает ее.
Вот почему, когда вы посмотрите технические характеристики автомобиля в автомобильном журнале, вы увидите указания как для мощности, так и для крутящего момента.
Мощность и производительность
То, что мы называем «высокопроизводительным» автомобилем, — это просто транспортное средство с большой мощностью и небольшим весом. Таким образом, соотношение мощности к массе является важнейшим критерием для высокопроизводительного автомобиля. Типичным примером может служить Ferrari, мощность которого может составлять 800 лошадиных сил на автомобиль весом 3500 фунтов. Это ставит отношение мощности к весу примерно на 0.229. Для сравнения, Ford Explorer, который продается примерно за десятую часть цены Ferrari, может иметь около 300 лошадиных сил, чтобы переместить около 4500 фунтов. Его удельная мощность будет намного ниже, примерно 0,067. Ferrari разгонится с места до 100 км намного быстрее, чем Ford Focus.
На этом этапе должно быть ясно, почему калькуляторы используют уравнения, основанные на весе, времени и скорости для расчета мощности.
Калькулятор BMR
Калькулятор базовой скорости метаболизма (BMR) оценивает вашу базальную скорость метаболизма — количество энергии, израсходованной в состоянии покоя в нейтрально умеренной среде и в постабсорбтивном состоянии (это означает, что пищеварительная система неактивна, что требует около 12 часов голодания).
Результат
BMR = 1605 калорий в день
Ежедневная потребность в калориях в зависимости от уровня активности
| Уровень активности | Калорий |
| Сидячий образ жизни: мало или совсем не упражнения | —1926 |
| 2,207 | |
| Упражнения 4-5 раз в неделю | 2,351 |
| Ежедневные упражнения или интенсивные упражнения 3-4 раза в неделю | 2,488 |
| Интенсивные упражнения 6-7 раз / неделя | 2,769 |
| Ежедневные очень интенсивные упражнения или физическая работа | 3,050 |
Упражнение: 15-30 минут повышенной активности пульса.
Интенсивные упражнения: 45–120 минут повышенной активности пульса.
Очень интенсивные упражнения: 2+ часа повышенной активности пульса.
Калькулятор связанного с телом жира | Калькулятор калорий
Базальная скорость метаболизма (BMR) — это количество энергии, необходимое для отдыха в умеренном климате, когда пищеварительная система неактивна. Это эквивалентно выяснению, сколько бензина потребляет неработающий автомобиль, когда он припаркован. В таком состоянии энергия будет использоваться только для поддержания жизненно важных органов, включая сердце, легкие, почки, нервную систему, кишечник, печень, легкие, половые органы, мышцы и кожу.Для большинства людей около 70% общей энергии (калорий), сжигаемой каждый день, приходится на содержание. Физическая активность составляет ~ 20% расходов, а ~ 10% используется для переваривания пищи, также известного как термогенез.
BMR измеряется в очень строгих условиях в состоянии бодрствования. Для точного измерения BMR необходимо, чтобы симпатическая нервная система человека была неактивна, а это означает, что человек должен быть полностью отдохнувшим. Основной обмен веществ обычно является самым большим компонентом общих потребностей человека в калориях.Суточная потребность в калориях — это значение BMR, умноженное на коэффициент от 1,2 до 1,9, в зависимости от уровня активности.
В большинстве случаев BMR оценивается с помощью уравнений, полученных на основе статистических данных. Уравнение Харриса-Бенедикта было одним из первых введенных уравнений. Он был пересмотрен в 1984 году для большей точности и использовался до 1990 года, когда было введено уравнение Миффлина-Сент-Джера. Было показано, что уравнение Миффлина-Сент-Джера более точное, чем пересмотренное уравнение Харриса-Бенедикта.Формула Кэтча-Макардла немного отличается тем, что рассчитывает дневные затраты энергии в состоянии покоя (RDEE) с учетом безжировой массы тела, чего не делают ни Миффлин-Сент-Джор, ни уравнение Харриса-Бенедикта. Из этих уравнений наиболее точным уравнением для расчета BMR считается уравнение Миффлина-Сент-Джера, за исключением того, что формула Кетча-МакАрдла может быть более точной для людей, которые стройнее и знают процентное содержание жира в организме. Вы можете выбрать уравнение, которое будет использоваться в расчетах, развернув настройки.
Три уравнения, используемые калькулятором, перечислены ниже:
Уравнение Mifflin-St Jeor:
Для мужчин:
BMR = 10Вт + 6.25H — 5A + 5
Для женщин:
BMR = 10Вт + 6.25H — 5A — 161
Пересмотренное уравнение Харриса-Бенедикта:
Для мужчин:
BMR = 13,397 Вт + 4,799 ч — 5,677A + 88,362
Для женщин:
BMR = 9,247 Вт + 3,098 ч — 4,330 A + 447,593
Формула Кэтча-Макардла:
BMR = 370 + 21.6 (1 — F) ш
где:
W — масса тела в кг
H — рост в см
А возраст
F — телесный жир в процентах
Переменные BMR
Muscle Mass — Аэробные упражнения, такие как бег или езда на велосипеде, не влияют на BMR. Однако анаэробные упражнения, такие как поднятие тяжестей, косвенно приводят к более высокому BMR, потому что они наращивают мышечную массу, увеличивая потребление энергии в состоянии покоя. Чем больше мышечной массы в физическом составе человека, тем выше BMR требуется для поддержания его тела на определенном уровне.
Возраст — Чем старше и гибче человек, тем ниже его BMR или тем ниже минимальное потребление калорий, необходимое для поддержания функционирования его органов на определенном уровне.
Генетика — Наследственные черты, переданные от предков, влияют на BMR.
Weather — Холодная среда повышает BMR из-за энергии, необходимой для создания гомеостатической температуры тела. Точно так же слишком много внешнего тепла может повысить BMR, поскольку тело расходует энергию на охлаждение внутренних органов.BMR увеличивается примерно на 7% с каждым увеличением внутренней температуры тела на 1,36 градуса по Фаренгейту.
Диета — Небольшие регулярные порции пищи увеличивают BMR. С другой стороны, голодание может снизить BMR на 30%. Подобно телефону, который переходит в режим энергосбережения в течение последних 5% заряда батареи, человеческое тело будет приносить жертвы, такие как уровень энергии, настроение, поддержание физического состояния и функций мозга, чтобы более эффективно использовать то небольшое количество калорий. энергия используется для его поддержания.
Беременность — Обеспечение существования отдельного плода изнутри увеличивает BMR. Вот почему беременные женщины едят больше обычного. Кроме того, менопауза может увеличивать или уменьшать BMR в зависимости от гормональных изменений.
Добавки — Некоторые добавки или лекарства повышают BMR, в основном, чтобы способствовать снижению веса. Кофеин — обычное дело.
BMR Испытания
Онлайн-тесты BMR с жесткими формулами — не самый точный метод определения BMR человека.Лучше проконсультироваться у сертифицированного специалиста или измерить BMR калориметрическим прибором. Эти портативные устройства доступны во многих клубах здоровья и фитнеса, кабинетах врачей и клиниках похудания.
Скорость обмена веществ в покое
Хотя эти два понятия используются как синонимы, между их определениями есть ключевое различие. Скорость метаболизма в состоянии покоя или сокращенно RMR — это скорость, с которой организм сжигает энергию в расслабленном, но не полностью неактивном состоянии. Его также иногда определяют как расход энергии в состоянии покоя или РЗЭ.Измерения BMR должны соответствовать общему физиологическому равновесию, в то время как условия измерения RMR могут быть изменены и определены контекстными ограничениями.
Современная мудрость
Проведенное в 2005 году метааналитическое исследование BMR * показало, что при контроле всех факторов скорости метаболизма между людьми все еще существует неизвестная разница в 26%. По сути, средний человек, соблюдающий среднюю диету, вероятно, будет иметь ожидаемые значения BMR, но есть факторы, которые все еще не поняты, которые точно определяют BMR.
Следовательно, все расчеты BMR, даже с использованием самых точных методов, проводимых специалистами, не будут идеально точными в их измерениях. Еще не все функции человеческого тела хорошо изучены, поэтому расчет общего суточного расхода энергии (TDEE), полученный из оценок BMR, является всего лишь оценкой. При работе над достижением каких-либо целей в области здоровья или фитнеса BMR может помочь заложить основы, но с этого момента ему больше нечего предложить. Рассчитанный BMR и, следовательно, TDEE могут привести к неудовлетворительным результатам из-за их приблизительных оценок, но ведения ежедневного журнала упражнений, потребления пищи и т. Д., может помочь отследить факторы, которые приводят к каким-либо результатам, и помочь определить, что работает, а также что необходимо улучшить. Отслеживание прогресса в указанном журнале и внесение изменений с течением времени по мере необходимости, как правило, является лучшим показателем прогресса в достижении личных целей.
Номер ссылки
* Johnstone AM, Murison SD, Duncan JS, Rance KA, Speakman JR, Факторы, влияющие на изменение базальной скорости метаболизма, включают массу без жира, массу жира, возраст и циркулирующий тироксин, но не пол, циркулирующий лептин или трийодтиронин1.Am J Clin Nutr 2005; 82: 941-948.
Как рассчитать передаточное число и не сходить с ума
Когда вы впервые погрузитесь в мир шестерен, вы можете встретить несколько терминов: передаточное число и передаточное отношение. Вам не нужно знать, как рассчитать передаточное число, чтобы выбрать правильное, как вы можете найти в описании продукта, но понимание того, как это работает, сделает ваш выбор более… расчетливым. Используйте эту статью как свой личный фонарик, и вы не заблудитесь.
Чтобы упростить не только на словах, но и наглядно, мы постарались объяснить все с помощью Lego.Итак, приступим, или, как говорят аквалангисты, промокнем!
Семья Big Gears
Сначала было Колесо. Затем появился Gear. Шестерни вступают в игру по одной из следующих причин:
- для изменения направления вращения
- для синхронизации вращения
- для увеличения или уменьшения скорости вращения
- для перемещения вращательного движения на другую ось
Человечество знает зубчатые передачи (известные как «поезда») по крайней мере с четырех веков до нашей эры в Китае, поэтому первое изобретение может быть даже намного старше.За эти 2000 лет они развились и разделились на многочисленные династии. Назовем некоторых из самых влиятельных представителей. В зависимости от ориентации осей зубчатых колес существуют три большие группы поездов:
I. Поезда с параллельными осями: зубья параллельны оси
1. Шпора
Когда кто-то слышит слово «шестерня», в большинстве случаев ему на ум приходит простая прямозубая шестерня. Тип
Spur применяется во многих отраслях промышленности, и его легче всего найти на рынке всех размеров.
2. Спиральная
Цилиндрическая шестерня с геликоидальными зубьями (они расположены под углом к оси вращения шестерни) может выдерживать большую нагрузку, чем прямозубая, но они менее эффективны. Во время движения между двумя косозубыми шестернями возникают скользящие контакты, которые создают осевое усилие валов шестерен и повышают нагрев.
3. Рейка и шестерня
Это линейная шестерня (рейка), состоящая из прямозубой шестерни (шестерни). Вращательное движение шестерни вызывает поступательное движение рейки.Вращение рейки вызывает вращение шестерни. Эта система представляет собой простейший инструмент для преобразования вращательного движения в поступательное и обратное. Вы можете узнать больше о линейных приводах и их преимуществах здесь.
4. Внутренние шестерни
Это еще один цилиндрической формы, но зубцы здесь внутри кольца. Как показывает практика, эти шестерни встречаются в планетарных механизмах. Благодаря такой конструкции вибрации и потери в планетарных приводах незначительны. Стабильность вращения повышает надежность и повторяемость движения.Планетарные приводы предлагают большую эффективность и точность, чем другие системы.
II. Поезда с пересекающимися осями: место пересечения оси шестерни в точке
1. Фаска
В конической передаче оси валов пересекаются. Обычно угол между валами составляет 90 градусов, но шлейф существует и с другими углами (кроме 0 и 180 градусов). Такая гибкость угла позволяет нам широко использовать систему скоса для изменения направления силы. Например, из горизонтального в вертикальный.По форме и количеству зубьев различают угловые, спиральные и прямые конические шестерни.
III. Системы непараллельных осей:
1. Червячные и червячные колеса
Червячная передача состоит из обычной прямозубой шестерни (червячного колеса) и шестерни с одним зубом (червяк), но этот зуб похож на резьбу винта. Движение колеса и шестерни представляет собой смесь скольжения и качения. Скользящие движения вызывают трение и нагрев, которые снижают эффективность поезда до 50%.В то же время этот тип сетки обеспечивает очень тихую работу, что делает червяк подходящим для использования в средах, где необходимо минимизировать шум. Даже при относительно низком КПД червячные передачи обеспечивают очень высокие передаточные числа.
2. Винт
Винтовой механизм представляет собой пару косозубых шестерен, передающих движение и мощность между перпендикулярными, но не пересекающимися валами. Во время взаимодействия они совершают не стандартное перекатывающее движение, а винтовое движение (поэтому винт).
Передаточное число
Каждый упомянутый тип поезда имеет свои сильные и слабые стороны, но основным параметром зацепляющих шестерен по-прежнему является передаточное число . Поскольку каждая часть поезда имеет разное количество зубьев, каждая из шестерен вращается с разной скоростью. Передаточное число показывает эту разницу.
Знание соотношения в роботизированном проекте имеет решающее значение для:
- Определение скорости вращения ведущей шестерни.
- Достижение баланса скорости и крутящего момента.Если передаточное число 1: 1, величина крутящего момента такая же, а скорость такая же. Например, при соотношении 1: 4 вы получите меньший крутящий момент, но большую скорость. При соотношении 4: 1 вы снизите скорость, но увеличите крутящий момент.
- Оптимальный размер серводвигателя. Если инерция двигателя слишком велика по сравнению с инерцией нагрузки, двигатель больше, а это означает, что он был дороже, чем необходимо для его производства, и двигатель потребляет больше энергии, чем необходимо для приложения.
- Минимизация ошибок и повышение точности.Идеальное передаточное число — это наименьший момент инерции, который может обеспечить максимальное ускорение, не делая систему нестабильной, перегретой или неточной.
Как рассчитать передаточное число?
Начнем с простейшей зубчатой передачи, в которой всего два зубчатых колеса. Первая шестерня, прикрепленная к валу двигателя, называется «приводом». Вторая шестерня, прикрепленная к валу нагрузки, — «ведомая».
Формулы вычисляемого поля | Документы Microsoft
- 15 минут на чтение
В этой статье
Применимо к: SharePoint Foundation 2010
В следующих таблицах представлена информация о различных типах формул, которые можно реализовать в вычисляемом поле с помощью формулы Microsoft.SharePoint.SPFieldCalculated класс.
Важные примечания
Примечание
ФормулыMicrosoft SharePoint Foundation для вычисляемых полей основаны на функциях и синтаксисе Microsoft Excel. Однако Microsoft поддерживает только те функции, которые упомянуты на этой странице, для использования в вычисляемых полях SharePoint Foundation. Например, функция Excel MID не поддерживается.
Важно
Во всех примерах формул в этом разделе в качестве символа-разделителя параметра используются запятые «,».В некоторых странах запятая зарезервирована для использования в качестве десятичного знака. В таких странах пользователи, создающие вычисляемое поле, должны использовать точку с запятой «;» как символ-разделитель. Независимо от того, какой символ используется при создании поля, формула работает в списках на веб-сайтах SharePoint в любой точке мира. SharePoint автоматически изменяет символ-разделитель на тот, который соответствует языку / культуре текущей страницы. Например, предположим, что следующая формула создана на веб-сайте, региональные параметры которого — fr-fr (Франция): = IF (Number1> Number2; 5; 10).Если язык и региональные параметры веб-сайта затем изменяются на en-us (США), формула автоматически изменяется на: = IF (Number1> Number2,5,10).
Условные формулы
Следующие формулы можно использовать для проверки условия оператора и возврата значения «Да» или «Нет», для проверки альтернативного значения, такого как ОК или Не ОК, или для возврата пробела или дефиса для представления нулевого значения.
Определить, является ли число больше или меньше другого числа
Используйте функцию ЕСЛИ для выполнения этого сравнения.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
15000 | 9000 | = [Столбец1]> [Столбец2] | Столбец1 больше, чем Столбец2? (Да) |
15000 | 9000 | = ЕСЛИ ([Столбец1] <= [Столбец2], «ОК», «Не в порядке») | Столбец1 меньше или равен столбцу2? (Не в порядке) |
Вернуть логическое значение после сравнения содержимого столбца
Чтобы получить результат, являющийся логическим значением (Да или Нет), используйте функции И, ИЛИ и НЕ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15 | 9 | 8 | = И ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]) | 15 больше 9 и меньше 8? (Нет) |
15 | 9 | 8 | = ИЛИ ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]) | 15 больше 9 или меньше 8? (Да) |
15 | 9 | 8 | = НЕ ([Столбец1] + [Столбец2] = 24) | Разве 15 плюс 9 не равно 24? (Нет) |
Для результата, представляющего собой другое вычисление или любое другое значение, кроме Да или Нет, используйте функции ЕСЛИ, И и ИЛИ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15 | 9 | 8 | = ЕСЛИ ([Column1] = 15, «ОК», «Не в порядке») | Если значение в столбце 1 равно 15, вернуть «ОК».(ОК) |
15 | 9 | 8 | = ЕСЛИ (И ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]), «ОК», «Неверно») | Если 15 больше 9 и меньше 8, вернуть «ОК». (Не в порядке) |
15 | 9 | 8 | = ЕСЛИ (ИЛИ ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]), «ОК», «Не в порядке») | Если 15 больше 9 или меньше 8, вернуть «ОК».(ОК) |
Отображать нули как пробелы или тире
Чтобы отобразить ноль, выполните простое вычисление. Чтобы отобразить пробел или тире, используйте функцию ЕСЛИ.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
10 | 10 | = [Столбец1] — [Столбец2] | Второе число, вычитаемое из первого.(0) |
15 | 9 | = ЕСЛИ ([Столбец1] — [Столбец2], [Столбец1] — [Столбец2], «-») | Возвращает прочерк, если значение равно нулю. (-) |
Скрыть значения ошибок в столбцах
Чтобы отобразить тире, # N / A или NA вместо значения ошибки, используйте функцию ISERROR.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
10 | 0 | = [Столбец1] / [Столбец2] | Выдает ошибку (# DIV / 0) |
10 | 0 | = ЕСЛИ (ЕСТЬ ОШИБКА ([Столбец1] / [Столбец2]), «НЕТ», [Столбец1] / [Столбец2]) | Возвращает NA, если значение является ошибкой |
10 | 0 | = ЕСЛИ (ЕСТЬ ОШИБКА ([Столбец1] / [Столбец2]), «-», [Столбец1] / [Столбец2]) | Возвращает прочерк, если значение является ошибкой |
Формулы даты и времени
Вы можете использовать следующие формулы для выполнения вычислений, основанных на датах и времени, таких как добавление числа дней, месяцев или лет к дате, вычисление разницы между двумя датами и преобразование времени в десятичное значение.
Добавить даты
Чтобы добавить количество дней к дате, используйте оператор сложения (+).
Примечание
Когда вы управляете датами, тип возвращаемого значения вычисляемого столбца должен быть установлен на Дата и время.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 | 3 | = [Столбец1] + [Столбец2] | Добавляет 3 дня к 09.06.2007 (12.06.2007) |
10.12.2008 | 54 | = [Столбец1] + [Столбец2] | Добавляет 54 дня к 10.12.2008 (02.02.2009) |
Чтобы добавить количество месяцев к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 | 3 | = ДАТА (ГОД ([Столбец1]), МЕСЯЦ ([Столбец1]) + [Столбец2], ДЕНЬ ([Столбец1])) | Добавляет 3 месяца к 09.06.2007 (09.09.2007) |
10.12.2008 | 25 | = ДАТА (ГОД ([Столбец1]), МЕСЯЦ ([Столбец1]) + [Столбец2], ДЕНЬ ([Столбец1])) | Добавляет 25 месяцев к 10.12.2008 (01.10.2011) |
Чтобы добавить количество лет к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 | 3 | = ДАТА (ГОД ([Столбец1]) + [Столбец2], МЕСЯЦ ([Столбец1]), ДЕНЬ ([Столбец1])) | Добавляет 3 года к 09.06.2007 (09.06.2010) |
10.12.2008 | 25 | = ДАТА (ГОД ([Столбец1]) + [Столбец2], МЕСЯЦ ([Столбец1]), ДЕНЬ ([Столбец1])) | Добавляет 25 лет к 10.12.2008 (10.12.2033) |
Чтобы добавить к дате комбинацию дней, месяцев и лет, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
09.06.2007 | = ДАТА (ГОД ([Столбец1]) + 3, МЕСЯЦ ([Столбец1]) + 1, ДЕНЬ ([Столбец1]) + 5) | Добавляет 3 года, 1 месяц и 5 дней к 09.06.2007 (14.07.2010) |
10.12.2008 | = ДАТА (ГОД ([Столбец1]) + 1, МЕСЯЦ ([Столбец1]) + 7, ДЕНЬ ([Столбец1]) + 5) | Добавляет 1 год, 7 месяцев и 5 дней к 10.12.2008 (15.07.2010) |
Вычислить разницу между двумя датами
Используйте функцию РАЗНДАТ для выполнения этого вычисления.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
01 января 1995 | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «г») | Возвращает количество дней между двумя датами (1626) |
01 января 1995 | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «гм») | Возвращает количество месяцев между датами, игнорируя часть года (5) |
01 января 1995 | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «ярд») | Возвращает количество дней между датами, игнорируя часть года (165) |
Рассчитайте разницу между двумя умноженными на
Чтобы представить результат в стандартном формате времени (часы: минуты: секунды), используйте оператор вычитания (-) и функцию ТЕКСТ.Чтобы этот метод работал, часы не должны превышать 24, а минуты и секунды не должны превышать 60.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
06.09.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «h») | Часы между двумя точками (4) |
09.06.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «ч: мм») | Часы и минуты между двумя значениями (4:55) |
09.06.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «ч: мм: сс») | Часы, минуты и секунды между двумя значениями (4:55:00) |
Чтобы представить результат в виде суммы, основанной на одной единице времени, используйте функцию ЦЕЛОЕ или функцию ЧАС, МИНУТА или СЕКУНДА.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
06.09.2007 10:35 | 10.06.2007 15:30 | = ЦЕЛОЕ (([Столбец2] — [Столбец1]) * 24) | Общее количество часов между двумя временами (28) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЦЕЛОЕ (([Столбец2] — [Столбец1]) * 1440) | Всего минут между двумя значениями (1735) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЦЕЛОЕ (([Столбец2] — [Столбец1]) * 86400) | Всего секунд между двумя значениями (104100) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЧАС ([Столбец2] — [Столбец1]) | Часы между двумя моментами времени, когда разница не превышает 24 (4) |
09.06.2007 10:35 | 10.06.2007 15:30 | = МИНУТА ([Столбец2] — [Столбец1]) | Минуты между двумя моментами времени, когда разница не превышает 60 (55) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ВТОРОЙ ([Столбец2] — [Столбец1]) | Секунды между двумя моментами времени, когда разница не превышает 60 (0) |
Время пересчета
Чтобы преобразовать часы из стандартного формата времени в десятичное число, используйте функцию INT.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
10:35 | = ([Столбец1] -INT ([Столбец1])) * 24 | Количество часов с 00:00 (10,583333) |
12:15 | = ([Столбец1] -INT ([Столбец1])) * 24 | Количество часов с 00:00 (12.25) |
Чтобы преобразовать часы из десятичного числа в стандартный формат времени (часы: минуты: секунды), используйте оператор деления и функцию ТЕКСТ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23:58 | = ТЕКСТ (Столбец 1/24, «чч: мм: сс») | Часы, минуты и секунды с 00:00 (00:59:55) |
2:06 | = ТЕКСТ (Столбец 1/24, «ч: мм») | Часы и минуты с 00:00 (0:05) |
Вставить даты по юлианскому календарю
Юлианская дата относится к формату даты, который представляет собой комбинацию текущего года и количества дней с начала года.Например, 1 января 2007 года представлено как 2007001, а 31 декабря 2007 года представлено как 2007365. Этот формат не основан на юлианском календаре.
Чтобы преобразовать дату в юлианскую дату, используйте функции ТЕКСТ и ДАТАЗНАЧ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23.06.2007 | = ТЕКСТ ([Столбец1], «гг») & ТЕКСТ (([Столбец1] -ДАТАЗНАЧ («1/1 /» & ТЕКСТ ([Столбец1], «гг»)) + 1), «000») | Дата в юлианском формате с двузначным годом (07174) |
23.06.2007 | = ТЕКСТ ([Column1], «yyyy») & TEXT (([Column1] -DATEVALUE («1/1 /» & TEXT ([Column1], «yy»)) + 1), «000») | Дата в юлианском формате с четырехзначным годом (2007174) |
Чтобы преобразовать дату в юлианскую дату, которая используется в астрономии, используйте константу 2415018.50. Эта формула работает только для дат после 01.03.1901, и если вы используете систему дат 1900 года.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23.06.2007 | = [Столбец1] +2415018,50 | Дата в юлианском формате, используется в астрономии (2454274.50) |
Показывать даты как день недели
Чтобы преобразовать даты в текст дня недели, используйте функции ТЕКСТ и ДЕНЬ НЕДЕЛИ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
19 февраля 2007 г. | = ТЕКСТ (ДЕНЬ НЕДЕЛИ ([Столбец1]), «дддд») | Вычисляет день недели для даты и возвращает полное название дня (понедельник) |
3 января 2008 г. | = ТЕКСТ (ДЕНЬ НЕДЕЛИ ([Столбец1]), «ддд») | Вычисляет день недели для даты и возвращает сокращенное название дня (Чт) |
Математические формулы
Вы можете использовать следующие формулы для выполнения различных математических вычислений, таких как сложение, вычитание, умножение и деление чисел; вычисление среднего или медианы чисел; округление числа; и подсчет значений.
Сложите числа
Чтобы сложить числа в двух или более столбцах в строке, используйте оператор сложения (+) или функцию СУММ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
6 | 5 | 4 | = [Столбец1] + [Столбец2] + [Столбец3] | Суммирует значения в первых трех столбцах (15) |
6 | 5 | 4 | = СУММ ([Столбец1], [Столбец2], [Столбец3]) | Суммирует значения в первых трех столбцах (15) |
6 | 5 | 4 | = СУММ (ЕСЛИ ([Столбец1]> [Столбец2], [Столбец1] — [Столбец2], 10), [Столбец3]) | Если Column1 больше, чем Column2, складываются разница и Column3.В противном случае добавьте 10 и столбец 3 (5) |
Вычесть числа
Чтобы вычесть числа в двух или более столбцах в строке, используйте оператор вычитания (-) или функцию СУММ с отрицательными числами.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15000 | 9000 | -8000 | = [Столбец1] — [Столбец2] | Вычитает 9000 из 15000 (6000) |
15000 | 9000 | -8000 | = СУММ ([Столбец1], [Столбец2], [Столбец3]) | Добавляет числа в первые три столбца, включая отрицательные значения (16000) |
Вычислить разницу между двумя числами в процентах
Используйте операторы вычитания (-) и деления (/), а также функцию ABS.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
2342 | 2500 | = ([Столбец2] — [Столбец1]) / ABS ([Столбец1]) | Изменение в процентах (6,75% или 0,06746) |
Умножение чисел
Чтобы умножить числа в двух или более столбцах в строке, используйте оператор умножения (*) или функцию ПРОИЗВОД.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
5 | 2 | = [Столбец1] * [Столбец2] | Умножает числа в первых двух столбцах (10) |
5 | 2 | = ПРОДУКТ ([Столбец1], [Столбец2]) | Умножает числа в первых двух столбцах (10) |
5 | 2 | = ПРОДУКТ ([Столбец1], [Столбец2], 2) | Умножает числа в первых двух столбцах и число 2 (20) |
Разделить числа
Чтобы разделить числа на два или более столбца подряд, используйте оператор деления (/).
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
15000 | 12 | = [Столбец1] / [Столбец2] | Делит 15000 на 12 (1250) |
15000 | 12 | = ([Столбец1] +10000) / [Столбец2] | Складывает 15000 и 10000, а затем делит сумму на 12 (2083) |
Вычислить среднее значение
Среднее значение также называют средним.Чтобы вычислить среднее значение чисел в двух или более столбцах подряд, используйте функцию СРЕДНЕЕ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
6 | 5 | 4 | = СРЕДНЕЕ ([Столбец1], [Столбец2], [Столбец3]) | Среднее значение чисел в первых трех столбцах (5) |
6 | 5 | 4 | = СРЕДНЕЕ (ЕСЛИ ([Столбец1]> [Столбец2], [Столбец1] — [Столбец2], 10), [Столбец3]) | Если Column1 больше, чем Column2, вычислить среднее значение разницы и Column3.В противном случае вычислите среднее значение 10 и Столбец 3 (2,5) |
Вычислить медиану чисел
Медиана — это значение в центре упорядоченного диапазона чисел. Используйте функцию МЕДИАНА, чтобы вычислить медиану группы чисел.
A | Б | К | Д | E | Факс | Формула | Описание (результат) |
|---|---|---|---|---|---|---|---|
10 | 7 | 9 | 27 | 0 | 4 | = МЕДИАНА (A, B, C, D, E, F) | Медиана чисел в первых 6 столбцах (8) |
Вычислить наименьшее или наибольшее число в диапазоне
Чтобы вычислить наименьшее или наибольшее число в двух или более столбцах в строке, используйте функции MIN и MAX.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
10 | 7 | 9 | = МИН ([Столбец1], [Столбец2], [Столбец3]) | Наименьшее число (7) |
10 | 7 | 9 | = МАКС ([Столбец1], [Столбец2], [Столбец3]) | Наибольшее число (10) |
Значения счета
Для подсчета числовых значений используйте функцию СЧЁТ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
Apple | 12.12.2007 | = СЧЁТ ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество столбцов, содержащих числовые значения.Исключает дату и время, текст и пустые значения (0) | |
$ 12 | # DIV / 0! | 1.01 | = СЧЁТ ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество столбцов, содержащих числовые значения, но исключает ошибки и логические значения (2) |
Увеличение или уменьшение числа на процент
Используйте оператор процента (%) для выполнения этого вычисления.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) | |
|---|---|---|---|---|
23 | 3% | = [Столбец1] * (1 + 5%) | Увеличивает число в столбце 1 на 5% (24,15) | |
23 | 3% | = [Столбец1] * (1+ [Столбец2]) | Увеличивает число в столбце 1 на процентное значение в столбце 2: 3% (23.[Column2] | Вычисляет пять в квадрате (25) |
5 | 3 | = МОЩНОСТЬ ([Столбец1], [Столбец2]) | Вычисляет пять кубов (125) |
Округлить число
Чтобы округлить число, используйте функцию ОКРУГЛВВЕРХ, НЕЧЕТНО или ЧЕТНО.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20.3 | = ОКРУГЛ ВВЕРХ ([Столбец1], 0) | Округляет 20,3 до ближайшего целого числа (21) |
-5,9 | = ОКРУГЛ ВВЕРХ ([Столбец1], 0) | Округляет -5,9 до ближайшего целого числа (-5) |
12,5493 | = ОКРУГЛ ВВЕРХ ([Столбец1], 2) | Округляет 12,5493 до ближайшей сотой, до двух десятичных знаков (12,55) |
20.3 | = ЧЕТНЫЙ ([Столбец1]) | Округляет 20,3 до ближайшего четного числа (22) |
20,3 | = НЕЧЕТ ([Столбец1]) | Округляет 20,3 до ближайшего нечетного числа (21) |
Чтобы округлить число, используйте функцию ROUNDDOWN.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20.3 | = ОКРУГЛ ВНИЗ ([Столбец1], 0) | Округляет 20,3 до ближайшего целого числа (20) |
-5,9 | = ОКРУГЛ ВНИЗ ([Столбец1], 0) | Округляет -5,9 до ближайшего целого числа (-6) |
12,5493 | = ОКРУГЛ ВНИЗ ([Столбец1], 2) | Округляет 12,5493 до ближайшей сотой, до двух десятичных знаков (12.54) |
Чтобы округлить число до ближайшего числа или дроби, используйте функцию ОКРУГЛ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20,3 | = ОКРУГЛ ([Столбец1], 0) | Округляет 20,3 в меньшую сторону, поскольку дробная часть меньше 0,5 (20) |
5.9 | = ОКРУГЛ ([Столбец1], 0) | Округляет 5,9 в большую сторону, поскольку дробная часть больше 0,5 (6) |
-5,9 | = ОКРУГЛ ([Столбец1], 0) | Округляет -5,9 вниз, так как дробная часть меньше -,5 (-6) |
1,25 | = ОКРУГЛ ([Столбец1], 1) | Округляет число до ближайшей десятой (один десятичный знак).Поскольку округляемая часть составляет 0,05 или больше, число округляется в большую сторону (результат: 1,3) |
30,452 | = ОКРУГЛ ([Столбец1], 2) | Округляет число до ближайшей сотой (два десятичных знака). Поскольку округляемая часть, 0,002, меньше 0,005, число округляется в меньшую сторону (результат: 30,45) |
Чтобы округлить число до значащей цифры выше 0, используйте функции ROUND, ROUNDUP, ROUNDDOWN, INT и LEN.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
54 | = ОКРУГЛ ([Column1], 3-LEN (INT ([Column1]))) | Округляет число до трех значащих цифр (54 ) |
22230 | = ОКРУГЛ ВНИЗ ([Column1], 3-LEN (INT ([Column1]))) | Округляет нижнее число до трех значащих цифр (22200) |
54 | = ОКРУГЛ ВВЕРХ ([Столбец1], 5-ДЛСТР (ЦЕЛОЕ ([Столбец1]))) | Округляет верхнее число до 5 значащих цифр (54 |
Текстовые формулы
Следующие формулы можно использовать для управления текстом, например для объединения или конкатенации значений из нескольких столбцов, сравнения содержимого столбцов, удаления символов или пробелов и повторения символов.
Изменить регистр текста
Чтобы изменить регистр текста, используйте функцию ВЕРХНИЙ, НИЖНИЙ или ПРАВИЛЬНЫЙ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Нина Вьетцен | = ВЕРХНИЙ ([Столбец1]) | Переводит текст в верхний регистр (НИНА ВЬЕТЦЕН) |
Нина Вьетцен | = НИЖНИЙ ([Столбец1]) | Переводит текст в нижний регистр (нина вьетцен) |
Нина Вьетцен | = ПРАВИЛЬНО ([Столбец1]) | Заменяет текст на регистр (Нина Вьетзен) |
Объединить имя и фамилию
Чтобы объединить имя и фамилию, используйте оператор амперсанда (&) или функцию СЦЕПИТЬ.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Карлос | Карвалло | = [Столбец1] и [Столбец2] | Объединяет две струны (Карлос Карвалло) |
Карлос | Карвалло | = [Столбец1] & «» & [Столбец2] | Объединяет две строки, разделенные пробелом (Карлос Карвалло) |
Карлос | Карвалло | = [Столбец2] & «,» & [Столбец1] | Объединяет две строки, разделенные запятой и пробелом (Карвалло, Карлос) |
Карлос | Карвалло | = СЦЕПИТЬ ([Столбец2], «,», [Столбец1]) | Объединяет две строки, разделенные запятой (Карвалло, Карлос) |
Объединить текст и числа из разных столбцов
Чтобы объединить текст и числа, используйте функцию СЦЕПИТЬ, оператор амперсанда (&) или функцию ТЕКСТ и оператор амперсанда.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Ян | 28 | = [Столбец1] & «продано» & [Столбец2] & «единиц.» | Объединяет приведенное выше содержание во фразу (Ян продал 28 шт.) |
Dubois | 40% | = [Столбец1] & «продано» & ТЕКСТ ([Столбец2], «0%») & «от общих продаж.» | Объединяет приведенное выше содержание во фразу (Дюбуа продал 40% от общего объема продаж.) Примечание Функция ТЕКСТ добавляет форматированное значение столбца 2 вместо базового значения, равного 0,4. |
Ян | 28 | = СЦЕПИТЬ ([Столбец1], «продано», [Столбец2], «единиц.») | Объединяет приведенное выше содержание во фразу (Ян продал 28 шт.) |
Объединить текст с датой или временем
Чтобы объединить текст с датой или временем, используйте функцию ТЕКСТ и оператор амперсанда (&).
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Дата выставления счета | 5 июня 2007 г. | = «Дата выписки:» & ТЕКСТ ([Столбец2], «д-ммм-гггг») | Объединяет текст с датой (Дата выписки: 5 июня 2007 г.) |
Дата выставления счета | 5 июня 2007 г. | = [Столбец1] & «» & ТЕКСТ ([Столбец2], «ммм-дд-гггг») | Объединяет текст и дату из разных столбцов в один столбец (Дата выставления счета 05.06.2007) |
Сравнить содержимое столбца
Чтобы сравнить один столбец с другим столбцом или списком значений, используйте функции ТОЧНО и ИЛИ.
Столбец 1 | Столбец 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
BD122 | BD123 | = ТОЧНЫЙ ([Столбец1], [Столбец2]) | Сравнивает содержимое первых двух столбцов (№) |
BD122 | BD123 | = ТОЧНЫЙ ([Столбец1], «BD122») | Сравнивает содержимое Column1 и строки «BD122» (Да) |
Определить, соответствует ли значение столбца или его часть определенному тексту
Чтобы определить, соответствует ли значение столбца или его часть определенному тексту, используйте функции ЕСЛИ, НАЙТИ, ПОИСК и ЕЧИСЛО.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Vietzen | = ЕСЛИ ([Column1] = «Vietzen», «OK», «Not OK») | Определяет, является ли Столбец 1 Vietzen (ОК) |
Vietzen | = ЕСЛИ (ЕЧИСЛО (НАЙТИ («v», [Столбец1])), «ОК», «Не ОК») | Определяет, содержит ли Column1 букву v (ОК) |
BD123 | = ЕЧИСЛО (НАЙТИ («BD»; [Столбец1])) | Определяет, содержит ли столбец 1 BD (Да) |
Подсчитать непустые столбцы
Для подсчета непустых столбцов используйте функцию СЧЁТ.
Столбец 1 | Столбец 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
Продажи | 19 | = СЧЁТ ([Столбец1], [Столбец2]) | Подсчитывает количество непустых столбцов (2) | |
Продажи | 19 | = COUNTA ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество непустых столбцов (2) |
Удалить символы из текста
Чтобы удалить символы из текста, используйте функции LEN, LEFT и RIGHT.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Витамин A | = ЛЕВЫЙ ([Столбец1], LEN ([Столбец1]) — 2) | Возвращает 7 (9-2) символов, начиная слева (Витамин) |
Витамин B1 | = ПРАВО ([Столбец1], LEN ([Столбец1]) — 8) | Возвращает 2 (10-8) символа, начиная справа (B1) |
Удалить пробелы в начале и конце столбца
Чтобы удалить пробелы из столбца, используйте функцию ОБРЕЗАТЬ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Привет! | = ОБРЕЗАТЬ ([Столбец1]) | Удаляет пробелы в начале и в конце (Привет!) |
Повторение символа в столбце
Чтобы повторить символ в столбце, используйте функцию ПОВТОР.
Формула | Описание (возможный результат) |
|---|---|
= ПОВТОР («.», 3) | Повторяет период 3 раза (…) |
= ПОВТОР («-«, 10) | Повторяет тире 10 раз (———-) |
См. Также
Номер ссылки
SPFieldCalculated
Mathway | Решение задач с исчислением
Хотя мы рассматриваем очень широкий круг проблем, в настоящее время мы не можем помочь с этой конкретной проблемой.Я разговаривал со своей командой, и мы учтем это для будущих тренировок. Есть ли другая проблема, для решения которой вам нужна дополнительная помощь?
Mathway в настоящее время не поддерживает эту тему. Мы более чем рады ответить на любой математический вопрос, который может у вас возникнуть по этой проблеме.
Mathway в настоящее время не поддерживает «Спросите эксперта в прямом эфире по химии».Если это то, что вы искали, обратитесь в службу поддержки.
Mathway в настоящее время вычисляет только линейные регрессии.
Мы здесь, чтобы помочь вам с математическими вопросами.Если у вас возникнут проблемы с вводом ответов в онлайн-задание, вам потребуется помощь вашей школы.
Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточному времени. Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799.
JBM — Расчеты
Калькуляторы
ПРИМЕЧАНИЕ. JBM не гарантирует выполнение этих расчетов для ЛЮБОЙ цели.Не забывайте всегда руководствоваться здравым смыслом и проверять загрузку с помощью текущие данные производителя.
Если вы считаете, что функциональные возможности изменились, проверьте список изменения, потому что это, вероятно, есть! На вопросы по расчетам можно ответить на ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ.
Калькуляторы общей траектории
- Траектория
Расчет траектории на основе BC пули и информации об оружии.Входные данные включают начальную скорость, высоту прицела, расстояние хронографа, баллистический коэффициент, функция лобового сопротивления, линия визирования и углы наклона, а также атмосферные условия. Варианты вывода включают переменные диапазоны и выбор единиц измерения ветра и падения (дюймы, MOA и милы). Расчеты выполняется в предположении, что пуля представляет собой точечную массу. Высота и азимут итеративно исправляется для обеспечения правильного нуля. - Траектория — Дрейф
Это почти как Калькулятор траектории выше, но он включает в себя параметры закрутки ствола, направления закручивания и длины пули.Эти значения используются для расчета спинового дрейфа с использованием приближения разработан Брайаном Литцем и опубликован в его книге, Прикладная баллистика для стрельбы на большие дистанции. Коэффициент устойчивости рассчитывается по формуле устойчивости Миллера. При использовании библиотеки маркеров вы все равно должны вводить длину пули. потому что его нет в библиотеке. - Траектория — упрощенная
Многие люди не используют все термины на указанной странице расчета траектории выше, поэтому эта программа использует значения по умолчанию для входов, не установленных пользователем.Расчет выполняется той же программой, что и страница траектории. выше. - Modified Point Mass Trajectory
Расчет траектории на основе размеров пули. Этот тип траектории дает хорошую оценку для таких вещей, как дрейф вращения и стабильность. Я также добавил эффекты кориолиса. Он имеет значительное количество входы, так что будьте осторожны. Этот онлайн-расчет заменяет мои ранее доступные Программа MPM.
Карты дальности
Карты дальности рассчитывают падение пули для разных атмосферных условий. чем нулевые условия.Они делают это, вычисляя траекторию в нулевом условиях, а затем применяя нулевой угол возвышения к различным атмосферным условия. Для получения дополнительной информации см. Этот раздел.
Все эти калькуляторы определяют начальную скорость пули при температуре стрельбы по с использованием линейной интерполяции с учетом двух дульных скоростей и двух температур.
Все эти калькуляторы включают в себя снос вращения в качестве опции.
- Карты траектории
Карта диапазона для различных температур и высот.На выходе получается матрица значений падения пули и аэродинамики в зависимости от температуры и высоты плотность. - Микрокарты траектории
Карта малой дальности. Большинство входов такие же, как у большого карта траектории, но она также включает направление и скорость цели. Не могу включен, потому что это делает целевое отведение довольно сложным (если не бесполезным). Вывод включает только введенные вами примечания и таблицу. Таблица похожа на старую карту — падение, ветер и свинец в двух единицах. - Микрокарты траектории Только ветер
Маленькая карта дальности с тремя столбцами только значений ветра — без падения или цели вести. Эта карта не учитывает дрейф значений ветра. - Микрокарты траектории — постоянное падение
Карта небольшого диапазона, но с регулярными интервалами падения. Он делает это, находя диапазоны для которых падение кратно желаемым значениям (например, каждую минуту угла). Это приводит к нерегулярным диапазонам.Ветер отображается для диапазон и входная скорость ветра.
Максимальный диапазон
- Максимальное расстояние
Вычисляет максимальную дальность полета пули с учетом начальная скорость, баллистический коэффициент, вес и атмосферный условия.
Расчет и преобразование баллистических коэффициентов
- Ballistic Coefficients (Time)
Вычисляет баллистический коэффициент для ближней скорости, время полета, атмосферные условия и функция сопротивления. - Ballistic Coefficients (Velocity)
Вычисляет баллистический коэффициент для ближнего и дальнего скорости, атмосферные условия и функция сопротивления. - Bullet Drag and Twist
Рассчитывает CD пули и компоненты CD, требуемую крутку BC и стабильность для входной скрутки. Необходимые входные данные — это размеры пули. включая длину носа, общую длину, длину боаттейла, диаметр меплата, диаметр основания, калибр, вес, атмосферные условия и функция сопротивления.Этот алгоритм основан на работе Макдрага, проделанной Робертом МакКоем. См. Библиографию - Преобразование функции сопротивления
Преобразует единый баллистический коэффициент для одной функции сопротивления в баллистический коэффициент для другой функции сопротивления. Также рассчитывает секционный плотность и форм-факторы. - Преобразование массива функций перетаскивания
Преобразует массив баллистических коэффициентов в доступные функции перетаскивания и рекомендует использовать одну BC и функцию перетаскивания.Это чаще всего используется для преобразования нескольких BC в лучший единственный BC.
Коэффициент мощности и отдача
- Power Factor
Вычисляет коэффициент мощности и проверяет деления для IDPA, IPSC, TSA, USPSA и SASS. Вывод показывает, действительно ли деление сделано (зеленый / красный) и сколько в процентах.
